Зайцев А.П. Общая электротехника и электроника. Учебное пособие: Часть II

101

Этот пример иллюстрирует понятие веса разряда, т.е. различной его

значимости в десятичной системе счисления.

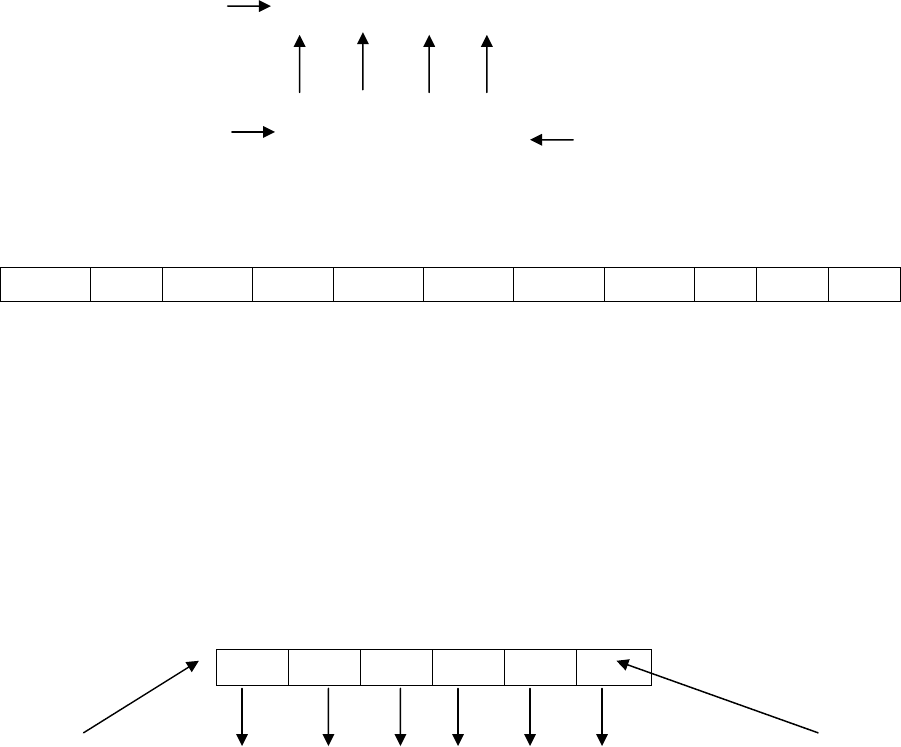
В двоичной системе счисления также используется понятие веса разря-

да. Так, для двоичного числа 1101 («один-один-ноль-один») справедливо:

Вес разряда 8 4 2 1

Двоичное число 1 1 0 1 . Двоичная точка

Вес разряда каждый раз получается как результат умножения веса

предыдущего разряда на 2:

1024 512 256 128 64 32 16 8 4 2 1.

Преобразование двоичных чисел в десятичные. Во время работы с циф-

ровыми устройствами приходится выполнять преобразование чисел из

двоичной системы в десятичную. Преобразование легко выполнить, зная

веса разрядов двоичного числа. Как и в случае с десятичными числами, де-

сятичный эквивалент двоичного числа определяется суммой значений раз-

рядных чисел, значения которых могут быть равны либо весу разряда, ли-

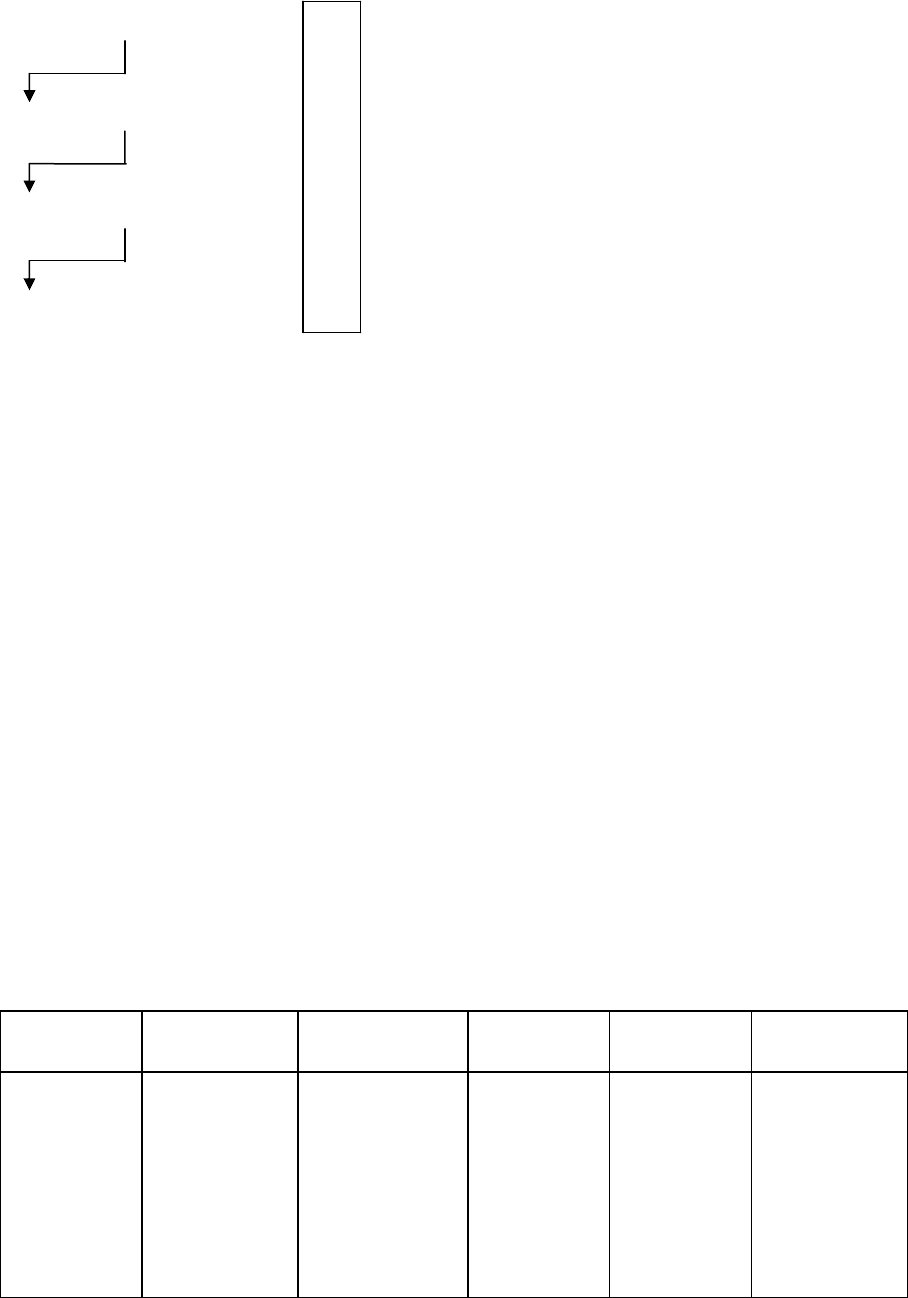
бо нулю. Так например, десятичный эквивалент двоичного числа 110101

определяется по схеме:

1 1 0 1 0 1.

Двоичное Двоичная

число 32 + 16 + 0 + 4 + 0 + 1 = 53 точка

Двигаясь влево от двоичной точки, необходимо под каждой двоичной

единицей подписать ее десятичный эквивалент и сложить получившиеся

числа.

Преобразование десятичных чисел в двоичные. Во время работы с

цифровыми устройствами такие преобразования необходимо проделывать

часто. Рассмотрим простой прием. Предположим, требуется преобразо-

вать число 13 в двоичное. Это можно сделать при помощи следующей

простой процедуры:

102

13 : 2 = 6 с остатком 1 - разряд с весом 1 (2

0

)

6 : 2 = 3 с остатком 0 - разряд с весом 2 (2

1

)

3 : 2 = 1 с остатком 1 - разряд с весом 4 (2

2

)

1 : 2 = 0 с остатком 1 - разряд с весом 8 (2

3

)

Двоичное число: 1101

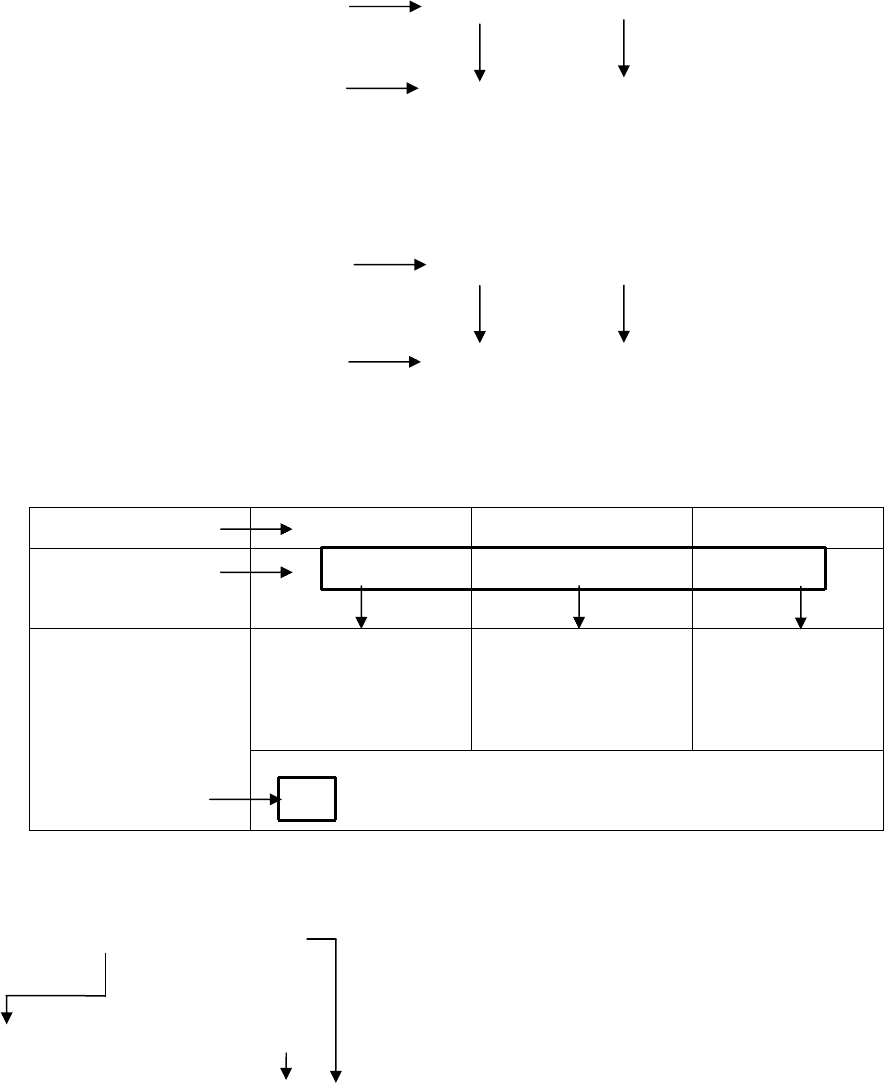
Сначала число 13 делим на 2 и получаем частное 6 и остаток 1. Этот

остаток становится значением разряда с весом 1. Затем 6 делим на 2, по-

лучаем частное 3 без остатка (0). Этот ноль записываем в разряд с весом 2.

Число 3 делим на 2 и остаток 1 записываем в разряд с весом 4. Наконец 1

делим на 2, получаем 0 и остаток 1, который записываем в старый разряд.

Отметим, что процесс деления на 2 следует заканчивать в тот момент,

когда получается частное, равное нулю.

Шестнадцатеричные числа. Преимущество шестнадцатеричной систе-

мы состоит в том, что при ее использовании можно реализовать непосред-

ственно преобразование четырехразрядных двоичных чисел. Шестнадца-

теричные коды обычно используют для представления многоразрядных

двоичных чисел: А6 → 10100110. Шестнадцатеричная система широко

применяется в микропроцессорных цифровых схемах для представления 8-

и 16-разрядных двоичных чисел.

Преобразование чисел из шестнадцатеричной в двоичную систему и

наоборот – типичные операции в микропроцессорах и микроЭВМ.

В шестнадцатеричной системе счисления применяются 16 символов:

Десятичное

число

Двоичное

число

Шестнадцате-

ричное число

Десятичное

число

Двоичное

число

Шестнадцате-

ричное число

0 0000 0 8 1000 8

1 0001 1 9 1001 9

2 0010 2 10 1010 А

3 0011 3 11 1011 В

4 0100 4 12 1100 С

5 0101 5 13 1101 D

6 0110 6 14 1110 Е

7 0111 7 15 1111 F

103

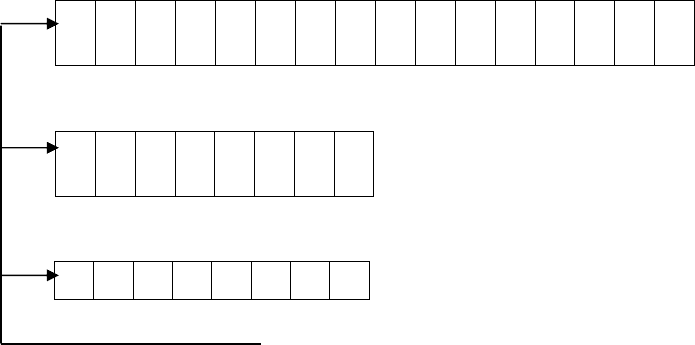
Перевод шестнадцатеричного числа в двоичное можно осуществить по

схеме:

Шестнадцатеричное число С 3

Двоичное число 1100 0011

При обратном переводе чисел необходимо двоичное число разбить на

тетрады, начиная с двоичной точки, и каждую тетраду представить шест-

надцатеричным эквивалентом:

Двоичное число 1110 1010

Шестнадцатеричное число Е А

Преобразование шестнадцатеричного числа в десятичный эквивалент

можно осуществить по следующей схеме:

Вес разряда 256 16 1

16-ричное

число

2 D B

256

×

2 = 512

16

×

13 = 208

1

×

11 = 11

Десятичное

число

512 + 208 + 11 =

731

Пример перевода десятичного числа в 16-ричное:

47 : 16 = 2 с остатком 15

2 : 16 = 0 с остатком 2

2 F

Аналогичным образом осуществляется перевод десятичного числа в

восьмеричное. При обратном переводе надо двоичное число разбить на

триады, начиная от двоичной точки, и каждую триаду представить восьме-

ричным эквивалентом.

104

Представление информации в ЭВМ. Наибольшее распространение в

ЭВМ имеет двоичная система счисления, т.к. для представления в маши-

не разряда двоичного числа может быть использован элемент, имеющий

всего два устойчивых состояния. Другим важным достоинством двоичной

системы является простота двоичной арифметики.

Недостатком двоичной системы является изображение числа в двоич-

ном коде числом разрядов в 3,3 раза большим, чем его представление в де-

сятичной системе. Поэтому в текстах программ для более короткой и

удобной записи двоичных кодов команд, адресов и операндов применяют-

ся восьмеричная и шестнадцатеричная системы счислений.

Любая информация (числа, команды, алфавитно-цифровые записи и

т.п.) представляется в ЭВМ в виде двоичных кодов (двоичных слов) фик-

сированной или переменной длины. Отдельные элементы двоичного кода,

имеющие значение 0 или 1, называют разрядами или битами. В ЭВМ сло-

ва часто разбивают на части, называемыми слогами или байтами.

В современных ЭВМ широко используется байт, содержащий 8 битов

(разрядов).

В ЭВМ применяют две формы представления чисел: с фиксированной

запятой (точкой) и с плавающей запятой (точкой). Эти формы называют

соответственно естественной и полулогарифмической. При представлении

чисел с фиксированной запятой положение запятой фиксируется в опреде-

ленном месте относительно разрядов числа. Обычно подразумевается, что

запятая находится или перед старшим разрядом (числа по модулю меньше

1), или после младшего (целые числа).

Когда не требуется высокой точности представления данных, то маши-

на имеет аппаратную возможность работать с байтами, диапазон представ-

ления чисел составляет (-127; +127). В этом случае старший разряд байта

является знаковым. Во всех случаях знаковый разряд равен 0 для положи-

тельных чисел и 1 для отрицательных чисел:

Слово

1

5

1

4

1

3

1

2

1

0

9 8 7 6 5 4 3 2 1 0

Старший байт

1

5

1

4

1

3

1

2

1

0

9 8

Младший байт

7 6 5 4 3 2 1 0

Знаковые разряды

105

Так как арифметико-логическое устройство ЭВМ выполняет опера-

ции вычитания при помощи сумматора, то отрицательные числа представ-

ляются в дополнительном коде. Введем понятие обратного и дополнитель-

ного кодов.

Для положительного числа Х его прямой, обратный и дополнитель-

ный коды совпадают. Для отрицательного числа Х все эти коды различны.

В двоичной системе счисления обратный код n-разрядного числа по-

лучают путем поразрядного инвертирования. Например, отрицательному

двоичному числу Х = - 00100100 соответствует обратный код (инверсия)

[Х]обр. = 11011011. Дополнительный код целого отрицательного числа

[Х]доп = [Х]обр +1.

Так, для предыдущего примера [Х]доп = 11011100.

9.2 ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА ИНТЕГРАЛЬНЫХ

МИКРОСХЕМАХ

9.2.1 Общие сведения о логических элементах

Основными составными частями цифровых схем являются логические

элементы, оперирующие с двоичными числами (двоичные логические эле-

менты). Они могут быть выполнены на транзисторах, диодах или инте-

гральных схемах.

Термин «логический» обычно применяют по отношению к процедуре

принятия решения. В этом смысле логический элемент - это такая схема,

которая, основываясь на входных сигналах, может решать, что ей ответить

на выходе – «да» или «нет» (логическая 1 или логический 0).

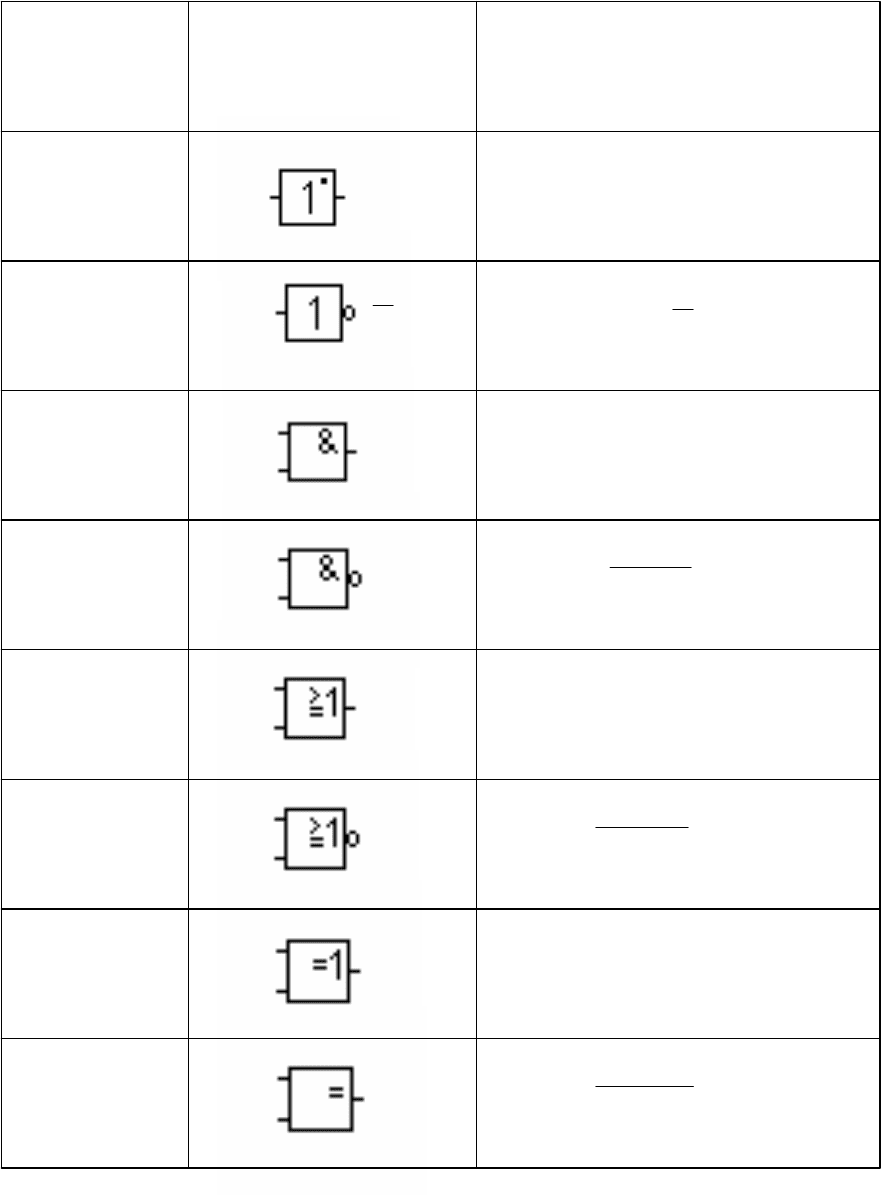
Существуют семь основных логических функций (табл. 9.1) и соответ-

ствующих им логических элементов: НЕ, И, И-НЕ, ИЛИ, ИЛИ-НЕ, исклю-

чающее ИЛИ, исключающее ИЛИ-НЕ. Черта над логической переменной

означает ее инверсию (превращение логической 1 в 0 и наоборот).

Таблица 9.1

ВЫХОД ВХОДЫ

ИЛИ ИЛИ-НЕ И И-НЕ

Исключающее

ИЛИ

Исключающее

ИЛИ-НЕ

X

1

X

2

F F F F F F

0 0 0 1 0 1 0 1

0 1 1 0 0 1 1 0

1 0 1 0 0 1 1 0

1 1 1 0 1 0 0 1

106

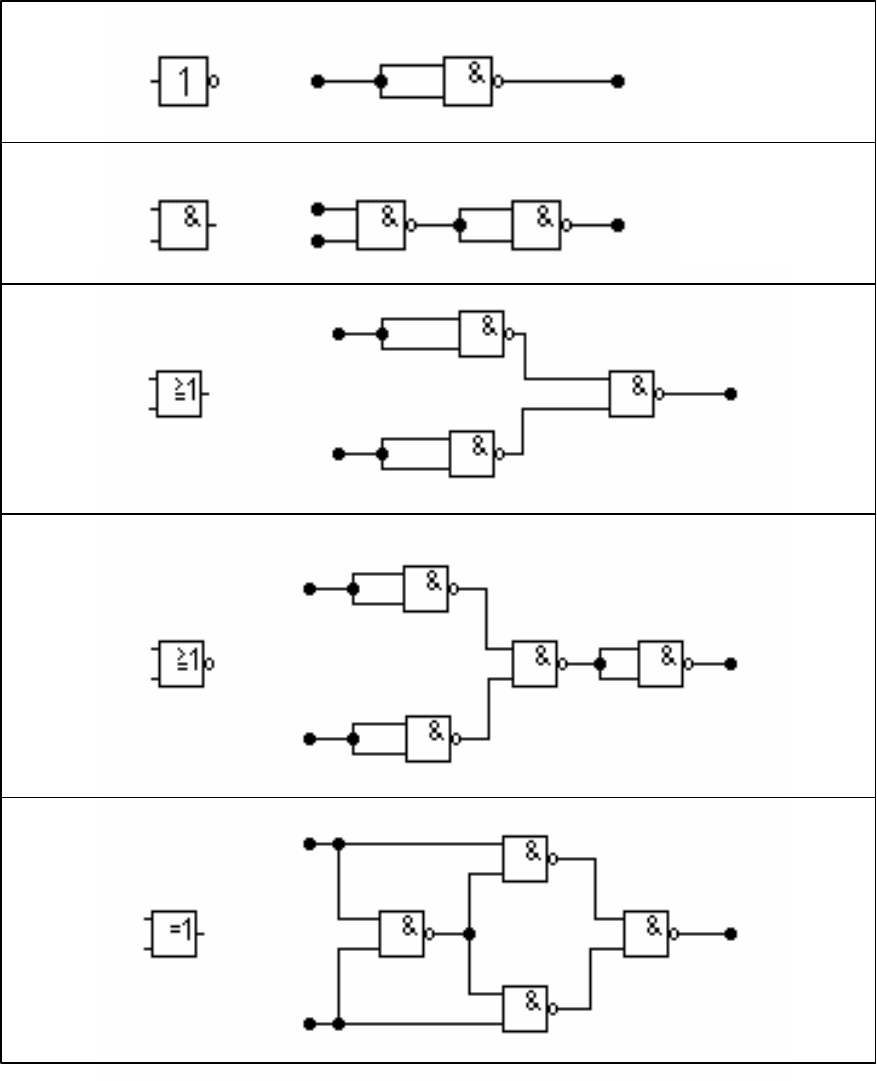
Любой логический элемент может быть определен условным графи-

ческим обозначением, описанием в виде таблицы истинности и в булевых

термах (табл. 9.2).

Таблица 9.2

В табл.9.2 знаком «⋅» обозначена конъюнкция, а знаком «+» – дизъ-

юнкция.

ИЛИ

И

НЕ

XX

=

Х

FХХ

21

=

⋅

1

Х

2

Х

F

1

Х

2

Х

F

Х

FXX

21

=⋅

1

Х

2

Х

F

1

Х

2

Х

F

1

Х

2

Х

F

1

Х

2

Х

FXX

21

=

+

FXX

21

=+

FXX

21

=

⊕

FXX

21

=⊕

элемен

т

Логический

еобозначени

еграфическо

Условное

функции логической

выражение Булево

Буфер

И

ХХ

=

НЕ

-

ИЛИ

НЕ

-

ИЛИ

еИсключающе

НЕ

-

е

Исключающе

107

Таблица истинности (сводная табл. 9.1) отражает все возможные ком-

бинации сигналов на входах и соответствующие сигналы на выходах

логических элементов.

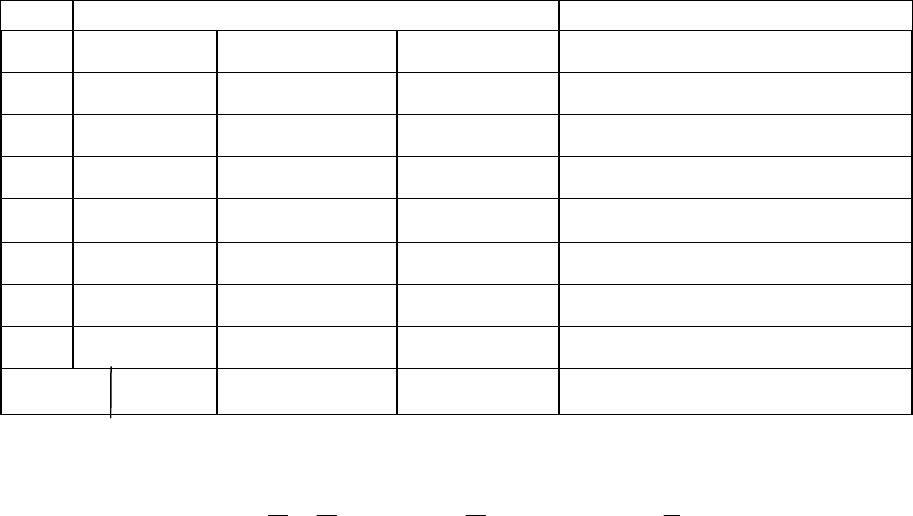
Логический элемент И-НЕ имеет универсальный характер в том смыс-

ле, что на его основе можно реализовать все другие логические элементы и

более сложные логические устройства.

Рис. 9.1

=

НЕ

И

НЕ-ИЛИ

ИЛИИскл.

ИЛИ Искл.

ИЛИ

108

9.2.2 Синтез комбинационных схем

Этапы синтеза. Синтез комбинационных схем (КС) выполняется в не-

сколько этапов, важнейшими из которых являются следующие:

1)

формализация условий на проектирование устройства, выполняю-

щего требуемые функции;

2)

получение математической модели устройства;

3)

разработка функциональной схемы устройства;

4)

разработка принципиальной схемы устройства.

Основной задачей, решаемой на 1-м этапе, является выбор способа опи-

сания устройства. Описание может выполняться в аналитической, матрич-

ной формах, либо в виде таблицы состояний.

На втором этапе необходимо получить математическую модель ком-

бинационного устройства в виде системы булевых функций в минималь-

ной нормальной дизъюнктивной (МНДФ), либо в минимальной нор-

мальной конъюнктивной (МНКФ) формах.

На третьем этапе осуществляется выбор функционально полного набо-

ра логических элементов, выбор базиса представления логических функ-

ций и минимизация модели устройства в этом базисе, составление функ-

циональной схемы и ее анализ, коррекция функциональной схемы по ре-

зультатам анализа.

На завершающем этапе выбирается тип физических элементов, реали-

зующих функциональную схему, составляется принципиальная схема,

проводится ее анализ и затем коррекция схемы по результатам анализа.

Математическое описание комбинационной схемы (КС). Математи-

ческое описание КС может быть получено в аналитической форме в виде

булевых функций. При этом исходная информация, определяющая условия

функционирования устройства, может задаваться в виде таблиц истинно-

сти, с помощью карт Карно и т.д. Так например, для КС с тремя входами X,

У, Z и с одним выходом F таблица истинности может иметь вид табл. 9.3.

Найти алгебраическое выражение функции, заданной таблицей истин-

ности, можно следующим образом.

1.

Алгебраическое выражение в ДСНФ находится по условиям ее ис-

тинности (по «1») и записывается в виде дизъюнкции элементарных

конъюнкций входных переменных, соответствующих каждой единице

функции, взятой из таблицы истинности. При этом под элементарной

конъюнкцией понимается логическое произведение переменных, взятых

со знаком инверсии, если значение переменной в таблице истинности рав-

но нулю, и без знака инверсии, если значение переменной равно единице.

Табл. 9.3 соответствует ДСНФ логической функции:

(9.1)

.ZYXZYXZYXZYXZYXF(1) ⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅=

109

2. Алгебраическое выражение функции в КСНФ находится по условию

ее ложности и записывается в виде конъюнкции элементарных дизъюнк-

ций, соответствующих каждому нулю функции F, взятому из таблицы ис-

тинности.

Таблица 9.3

N Комбина

ц

ия вхо

д

ных пе

р

еменных Выхо

д

ная

фу

нк

ц

ия

- X У Z F

0 0 0 0 1

1 0 0 1 0

2 0 1 0 1

3 0 1 1 1

4 1 0 0 1

5 1 0 1 0

6 1 1 0 0

7 1 1 1 1

Для рассмотренного выше

примера КСНФ имеет вид:

(9.2)

Получение МДНФ и МКНФ логических функций при помощи матриц

булевых функций.

Получаемые рассмотренным способом логические функ-

ции в ДСНФ и КСНФ в большинстве случаев не являются самыми

простыми, и их физическая реализация не является оптимальной. Поэтому

перед технической реализацией функции должны быть максимально уп-

рощены, минимизированы, т.е. представлены в МДНФ или МКНФ. Мини-

мизация исходных функций может быть выполнена аналитически непо-

средственным их упрощением на основе правил логики алгебры. Однако

более эффективным методом минимизации, особенно при небольшом чис-

ле входных переменных, является метод, основанный на использовании

матриц булевых функций (карты Карно).

В основу матричного способа задания булевых функции положено

представление множества комбинаций входных переменных на плоскости.

Каждой комбинации аргументов соответствует определенная клетка мат-

рицы, а значения функции вписываются в клетки матрицы.

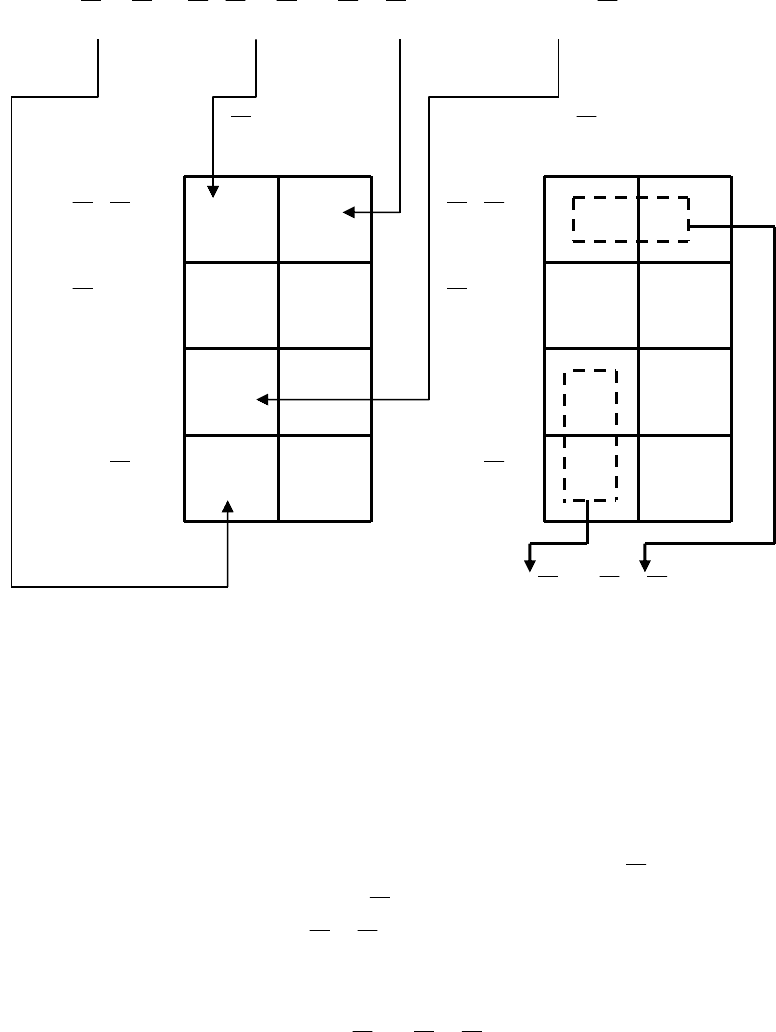
Карта Карно для булева выражения с тремя переменными, которое

представлено в совершенной дизъюнктивной нормальной форме (в каждом

минтерме содержатся прямое или инверсное значение всех переменных),

показана на рис. 9.2,

а. Имеются 8 возможных комбинаций переменных X1,

. )ZY(XZ)Y(XZ)YX(F(0) ++⋅++⋅++=

110

Х2 и Х3, которые представлены квадратами на карте. В них занесены 4

единицы, отображающие каждый из четырех членов исходного булева вы-

ражения.

(9.3)

а б

Рис. 9.2

Заполненная карта Карно повторена на рис. 9.2, б, где каждая группа

из двух соседних единиц обведена контуром. Нижний контур содержит Х

2

и ее инверсию, вследствие чего их можно опустить (опускаемые перемен-

ные помечены знаком «}»). После этого в составе нижнего контура сохра-

няются лишь X

1

и инверсия Х3, которые дают член .

В верхний контур входят Х

3 и , поэтому они опускаются, в результа-

те чего остается только член

Булево выражение в ДНФ получается введением операции ИЛИ

(9.4)

Упрощенное булево выражение описывается той же таблицей истинно-

сти, что и исходное.

Чтобы построить матрицы булевых функций (МБФ) n переменных,

необходимо выбрать способ кодирования клеток матрицы комбинациями

входных переменных. Если n

− четное число, то матрица вычерчивается в

FXXXXXXXXXXXX

3

213

2132

1

32

1

=⋅⋅+⋅⋅+⋅⋅+⋅⋅

3

X

3

X

3

X

3

X

21

XX

21

XX

2

1

XX

2

1

XX

21

XX

21

XX

2

1

XX

2

1

XX

1

11

1

FXXXX

213

1

=⋅+⋅

}

3

1

XX ⋅

3

X

.XX

21

⋅

.FXXXX

213

1

=⋅+⋅

а)

б)

Зайцев А.П. Общая электротехника и электроника. Учебное пособие: Часть II

Подождите немного. Документ загружается.