Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории
Подождите немного. Документ загружается.

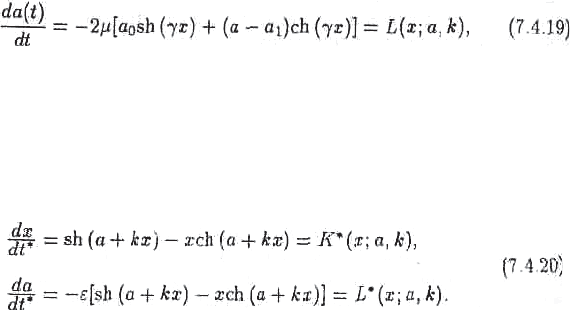
ɪɚɡɭɦɧɨɝɨ ɩɪɚɤɬɢɰɢɡɦɚ. ɗɬɨ ɩɪɢɜɨɞɢɬ ɤ ɩɨɹɜɥɟɧɢɸ ɥɭɱɲɟɣ ɩɪɨɞɭɤɰɢɢ,
ɩɥɚɧɢɪɨɜɚɧɢɸ ɢɧɜɟɫɬɢɰɢɣ, ɪɚɫɲɢɪɹɸɳɢɯ ɩɪɨɢɡɜɨɞɫɬɜɨ ɢ ɜɫɥɟɞɫɬɜɢɟ ɷɬɨɝɨ
ɜɵɧɭɠɞɚɟɬ ɨɫɬɚɥɶɧɵɯ ɤ ɩɨɞɪɚɠɚɧɢɸ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɯ ɩɨɥɢɬɢɤɚ ɪɚɫɲɢɪɟɧɢɹ
ɩɪɨɢɡɜɨɞɫɬɜɚ ɢ ɭɥɭɱɲɟɧɢɹ ɤɚɱɟɫɬɜɚ ɜɵɡɵɜɚɟɬ ɫɢɧɯɪɨɧɢɡɚɰɢɸ, ɱɬɨ ɛɭɞɟɬ ɧɚɛɥɸɞɚɬɶɫɹ
ɤɚɤ ɹɜɥɟɧɢɟ ɰɢɤɥɚ ɠɢɡɧɢ ɩɪɨɞɭɤɰɢɢ. Ɇɵ ɜɢɞɢɦ, ɱɬɨ ɜ ɫɨɝɥɚɫɢɢ ɫ ɷɬɢɦ ɪɚɫɫɭɠɞɟɧɢɟɦ
ɭɪɚɜɧɟɧɢɟ ɞɜɢɠɟɧɢɹ ɚɥɶɬɟɪɧɚɬɨɪɚ ɚ, ɤɨɬɨɪɵɣ
ɜ ɬɟɪɦɢɧɚɯ ɚɝɪɟɝɢɪɨɜɚɧɧɵɯ
ɩɟɪɟɦɟɧɧɵɯ ɨɬɪɚɠɚɟɬ ɢɡɦɟɧɟɧɢɟ ɞɟɹɬɟɥɶɧɨɫɬɢ ɩɪɟɞɩɪɢɧɢɦɚɬɟɥɟɣ ɜ ɪɚɡɥɢɱɧɵɯ
ɨɛɥɚɫɬɹɯ ɩɪɨɦɵɲɥɟɧɧɵɯ ɢɧɜɟɫɬɢɰɢɣ, ɩɪɢ ɨɝɨɜɨɪɟɧɧɵɯ ɜɵɲɟ ɭɫɥɨɜɢɹɯ ɞɨɥɠɧɨ
ɩɨɪɨɠɞɚɬɶ ɩɟɪɟɤɥɸɱɟɧɢɹ. Ʉɚɤ ɫɤɚɡɚɧɨ ɜ ɤɧɢɝɟ ȼɚɣɞɥɢɯɚ ɢ ɏɚɚɝɚ (1983),
ɩɨɬɟɧɰɢɚɥɶɧɨ ɩɨɞɯɨɞɹɳɢɣ ɜɢɞ ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɩɨɜɟɞɟɧɢɹ ɦɨɠɟɬ ɛɵɬɶ ɡɚɞɚɧ ɭɪɚɜ-
ɧɟɧɢɟɦ
ɝɞɟ L — ɜɵɧɭɠɞɚɸɳɚɹ ɫɢɥɚ ɪɟɮɨɪɦɚɬɨɪɫɤɨɣ ɫɬɪɚɬɟɝɢɢ, ȝ — ɩɚɪɚɦɟɬɪ
ɫɬɪɚɬɟɝɢɱɟɫɤɨɣ ɝɢɛɤɨɫɬɢ, ɨɬɪɚɠɚɸɳɢɣ ɝɢɛɤɨɫɬɶ ɢɧɜɟɫɬɨɪɨɜ ɨɬɧɨɫɢɬɟɥɶɧɨ ɢɡɦɟɧɟɧɢɹ
ɫɬɪɚɬɟɝɢɢ ɨɬ ɷɤɫɩɚɧɫɢɨɧɧɨɣ ɤ ɪɚɰɢɨɧɚɥɢɡɚɰɢɨɧɧɨɣ ɢ ɨɛɪɚɬɧɨ, Ȗ — ɩɚɪɚɦɟɬɪ ɫɤɨɪɨɫɬɢ
ɬɟɧɞɟɧɰɢɢ ɤ ɩɨɜɨɪɨɬɭ, Į
1
— ɩɚɪɚɦɟɬɪ ɜɥɢɹɧɢɹ ɫɬɪɚɬɟɝɢɢ, ɩɨɥɨɠɢɬɟɥɶɧɵɣ ɢɥɢ
ɨɬɪɢɰɚɬɟɥɶɧɵɣ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɬɟɦ, ɹɜɥɹɟɬɫɹ ɜɟɫɶ ɩɟɪɢɨɞ ɜ ɰɟɥɨɦ ɷɤɫɩɚɧɫɢɨɧɧɵɦ
ɢɥɢ ɪɚɰɢɨɧɚɥɢɡɚɰɢɨɧɧɵɦ, ɢ Į
0
— ɚɦɩɥɢɬɭɞɚ ɫɬɪɚɬɟɝɢɱɟɫɤɨɝɨ ɜɵɛɨɪɚ, ɤɨɬɨɪɚɹ
ɢɫɩɨɥɶɡɭɟɬɫɹ ɤɚɤ ɨɩɟɪɚɬɢɜɧɚɹ ɦɚɫɲɬɚɛɢɪɭɸɳɚɹ ɤɨɧɫɬɚɧɬɚ.
ɉɨɥɧɚɹ ɞɢɧɚɦɢɱɟɫɤɚɹ ɫɢɫɬɟɦɚ ɫɨɞɟɪɠɢɬ ɭɪɚɜɧɟɧɢɹ (7.4.18) ɢ (7.4.19). Ⱦɥɹ
ɩɪɨɫɬɨɬɵ ɜɜɟɞɟɦ ɩɟɪɟɦɟɧɧɵɟ t* = 2įt ɢ İ = ȝ/į. ɋɢɫɬɟɦɚ ɦɨɠɟɬ ɛɵɬɶ ɡɚɩɢɫɚɧɚ ɤɚɤ
ɋɭɳɟɫɬɜɨɜɚɧɢɟ ɪɚɜɧɨɜɟɫɢɣ ɜ ɧɟɣ ɥɟɝɤɨ ɝɚɪɚɧɬɢɪɨɜɚɬɶ, ɯɨɬɹ ɟɞɢɧɫɬɜɟɧɧɨɫɬɶ
ɩɨɤɚɡɚɬɶ ɧɟɥɶɡɹ. Ɏɚɤɬɢɱɟɫɤɢ, ɡɞɟɫɶ ɦɨɠɟɬ ɛɵɬɶ ɨɞɧɚ, ɬɪɢ ɢɥɢ ɩɹɬɶ ɬɨɱɟɤ ɪɚɜɧɨɜɟɫɢɹ,
ɤɨɬɨɪɵɟ ɡɚɜɢɫɹɬ ɬɨɥɶɤɨ ɨɬ ɤɨɧɤɪɟɬɧɵɯ ɡɧɚɱɟɧɢɣ ɩɚɪɚɦɟɬɪɨɜ. Ʉɪɨɦɟ ɬɨɝɨ, ɩɪɢɦɟɧɢɜ
ɬɟɨɪɢɸ ɉɭɚɧɤɚɪɟ-Ȼɟɧɞɢɤɫɨɧɚ, ȼɚɣɞɥɢɯ ɢ ɏɚɚɝ ɭɫɬɚɧɨɜɢɥɢ ɧɚɥɢɱɢɟ ɜ ɫɢɫɬɟɦɟ ɩɪɟɞɟ-
ɥɶɧɵɯ ɰɢɤɥɨɜ.
ȼ ɡɚɤɥɸɱɟɧɢɟ ɩɪɟɞɫɬɚɜɢɦ ɧɟɤɨɬɨɪɵɟ ɪɟɡɭɥɶɬɚɬɵ ɱɢɫɥɟɧɧɨɝɨ ɦɨɞɟɥɢɪɨɜɚɧɢɹ.
ȼɵɛɟɪɟɦ ɫɥɟɞɭɸɳɭɸ ɤɨɦɛɢɧɚɰɢɸ ɩɚɪɚɦɟɬɪɨɜ;
k = 1.5, Į
0
= 0.5, Į
1
= 0, Ȗ = 4.0, İ = 0.5.
ȼ ɷɬɨɦ ɫɥɭɱɚɟ k = 1.5 ɹɜɥɹɟɬɫɹ ɩɨɪɨɝɨɜɵɦ ɡɧɚɱɟɧɢɟɦ ɩɟɪɟɯɨɞɚ ɤ ɧɨɜɨɦɭ ɬɢɩɭ
ɪɟɲɟɧɢɹ. Ɂɞɟɫɶ ɩɪɨɹɜɥɹɟɬɫɹ ɤɪɢɬɢɱɟɫɤɨɟ ɜɨɡɞɟɣɫɬɜɢɟ
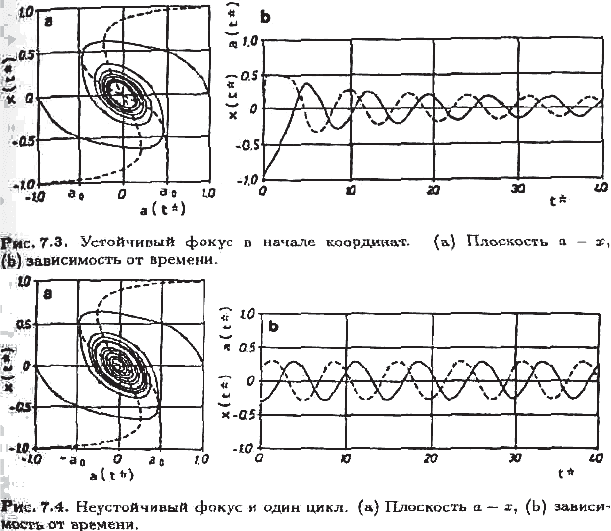
ɷɮɮɟɤɬɚ ɡɚɬɭɯɚɧɢɹ. ɏɨɬɹ ɧɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ ɹɜɥɹɟɬɫɹ ɟɞɢɧɫɬɜɟɧɧɵɦ ɪɚɜɧɨɜɟɫɢɟɦ, ɢ
ɨɧɨ ɭɫɬɨɣɱɢɜɨ, ɪɟɥɚɤɫɚɰɢɹ ɤɨɥɟɛɚɧɢɣ ɤɨɥɟɛɚɧɢɣ ɞɥɢɬɫɹ ɜ ɬɟɱɟɧɢɟ ɜɟɫɶɦɚ
ɡɧɚɱɢɬɟɥɶɧɨɝɨ ɜɪɟɦɟɧɢ. ɗɬɨɬ ɬɢɩ ɩɨɜɟɞɟɧɢɹ ɩɨɤɚɡɚɧ ɧɚ ɪɢɫ. 7.3 (ɫɦ. ɪɢɫ. 5.5 ɜ ɤɧɢɝɟ
ȼɚɣɞɥɢɯɚ ɢ ɏɚɚɝɚ).
ȿɫɥɢ ɜɡɹɬɶ ɫɥɟɞɭɸɳɢɟ ɡɧɚɱɟɧɢɹ ɩɚɪɚɦɟɬɪɨɜ:
k = 1.6, Į
0
= 0, Į
1
= 0, Ȗ = 4.0, İ = 0.5,
ɜɨɡɧɢɤɚɟɬ ɭɫɬɨɣɱɢɜɵɣ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ. ɇɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ
ɧɟɭɫɬɨɣɱɢɜɵɣ ɮɨɤɭɫ ɞɥɹ ɞɜɢɠɟɧɢɹ ɷɤɨɧɨɦɢɤɢ. ɗɬɨ ɩɨɜɟɞɟɧɢɟ ɢɥɥɸɫɬɪɢɪɭɟɬ ɪɢɫ. 7.4
(ɫɦ. ɪɢɫ. 5.6 ɜ ɤɧɢɝɟ ȼɚɣɞɥɢɯɚ ɢ ɏɚɚɝɚ).
ȼɚɣɞɥɢɯ ɢ ɏɚɚɝ ɩɪɢɦɟɧɢɥɢ ɫɜɨɸ ɦɨɞɟɥɶ ɤ ɢɫɫɥɟɞɨɜɚɧɢɸ ɷɤɨɧɨɦɢɤɢ Ɏɟɞɟɪɚɬɢɜɧɨɣ
Ɋɟɫɩɭɛɥɢɤɢ Ƚɟɪɦɚɧɢɢ ɜ ɩɟɪɢɨɞ 1955-1980 ɝɝ. ɇɚ ɪɢɫ. 7.5 ɩɨɤɚɡɚɧɵ ɪɟɡɭɥɶɬɚɬɵ
ɷɦɩɢɪɢɱɟɫɤɨɝɨ ɚɧɚɥɢɡɚ, ɫɨɫɬɚɜɥɟɧɧɵɟ ɢɡ ɧɟɫɤɨɥɶɤɢɯ
ɱɚɫɬɟɣ, ɤɨɬɨɪɵɟ ɫɨɨɬɜɟɬɫɬɜɭɸɬ
ɩɪɢɦɟɧɟɧɢɸ ɦɨɞɟɥɢ ɞɥɹ ɩɚɪɚɦɟɬɪɨɜ, ɩɪɢɧɚɞɥɟɠɚɳɢɯ ɬɪɟɦ ɢɧɬɟɪɜɚɥɚɦ ɜɪɟɦɟɧɢ:
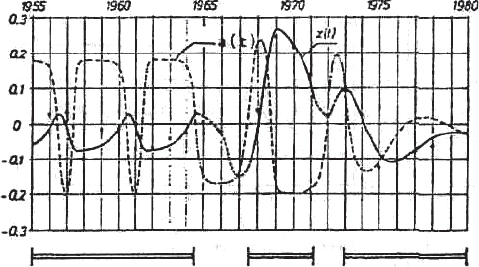
Ɋɢɫ. 7.5. ɋɪɚɜɧɟɧɢɟ ɪɟɡɭɥɶɬɚɬɨɜ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɦɨɞɟɥɢɪɨɜɚɧɢɹ ɢ ɞɚɧɧɵɯ
ɧɚɛɥɸɞɟɧɢɣ.
ɩɟɪɢɨɞɚɦ 1955-1965 ɝɝ., 1967-1971 ɝɝ. ɢ 1973-1980 ɝɝ. Ⱦɟɬɚɥɶɧɵɟ ɩɨɹɫɧɟɧɢɹ
ɪɟɡɭɥɶɬɚɬɨɜ ɞɚɧɵ ɜ ɤɧɢɝɟ ȼɚɣɞɥɢɯɚ ɢ ɏɚɚɝɚ (1983).
7.5. ȼɥɢɹɧɢɟ ɲɭɦɨɜ ɧɚ ɬɪɚɟɤɬɨɪɢɢ ɧɟɥɢɧɟɣɧɵɯ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ
ɫɢɫɬɟɦ ɜɛɥɢɡɢ ɨɫɨɛɵɯ ɬɨɱɟɤ
Ɇɵ ɩɨɤɚɡɚɥɢ, ɱɬɨ ɷɤɨɧɨɦɢɱɟɫɤɚɹ ɦɨɞɟɥɶ, ɭɱɢɬɵɜɚɸɳɚɹ ɜɥɢɹɧɢɟ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ
ɜɨɡɞɟɣɫɬɜɢɣ, ɞɨɥɠɧɚ ɨɬɪɚɠɚɬɶ ɫɬɟɩɟɧɶ, ɫ ɤɨɬɨɪɨɣ ɷɬɢ ɷɤɡɨɝɟɧɧɵɟ ɫɢɥɵ ɦɨɝɭɬ
ɩɨɜɥɢɹɬɶ ɧɚ ɤɨɧɟɱɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɦɨɞɟɥɢɪɨɜɚɧɢɹ. ȿɫɥɢ ɪɟɡɭɥɶɬɚɬɵ ɦɨɞɟɥɢɪɨɜɚɧɢɹ
ɪɟɲɚɸɳɢɦ ɨɛɪɚɡɨɦ ɡɚɜɢɫɹɬ ɨɬ ɷɤɡɨɝɟɧɧɵɯ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ ɫɢɥ ɢ ɜ ɦɚɥɨɣ ɫɬɟɩɟɧɢ
ɢɫɩɵɬɵɜɚɸɬ ɜɥɢɹɧɢɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɷɤɨɧɨɦɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ, ɦɨɞɟɥɶ ɧɟ
ɩɪɟɞɫɬɚɜɥɹɟɬ ɢɧɬɟɪɟɫɚ. ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɟɫɥɢ ɭɱɟɬ
ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ ɷɮɮɟɤɬɨɜ
ɨɤɚɡɵɜɚɟɬ ɦɚɥɨɡɚɦɟɬɧɨɟ ɜɥɢɹɧɢɟ ɧɚ ɤɚɱɟɫɬɜɟɧɧɵɟ ɪɟɡɭɥɶɬɚɬɵ, ɬɨ ɫɬɨɯɚɫɬɢɱɟɫɤɢɟ
ɮɚɤɬɨɪɵ ɦɨɝɭɬ ɛɵɬɶ ɩɨɥɧɨɫɬɶɸ ɢɫɤɥɸɱɟɧɵ ɢɡ ɚɧɚɥɢɡɚ. Ɉɞɧɚɤɨ, ɤɚɤ ɫɤɚɡɚɧɨ ɜ ɪɚɡɞ.
7.1, ɮɥɭɤɬɭɚɰɢɢ ɦɨɝɭɬ ɢɝɪɚɬɶ ɪɟɲɚɸɳɭɸ ɪɨɥɶ ɜ ɪɚɡɜɢɬɢɢ ɷɤɨɧɨɦɢɤɢ, ɞɚɠɟ ɟɫɥɢ
ɪɚɡɜɢɬɢɟ ɨɩɪɟɞɟɥɹɟɬɫɹ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɦɢ ɦɟɯɚɧɢɡɦɚɦɢ. ȼɥɢɹɧɢɟɦ ɮɥɭɤɬɭɚɰɢɢ ɧɚ
ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɟ ɪɚɡɜɢɬɢɟ ɧɟɥɶɡɹ ɩɪɟɧɟɛɪɟɱɶ ɜ ɫɥɭɱɚɟ, ɟɫɥɢ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɟ
ɭɪɚɜɧɟɧɢɹ ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɜɛɥɢɡɢ
ɤɪɢɬɢɱɟɫɤɢɯ ɬɨɱɟɤ.
ȼ ɩɪɟɞɵɞɭɳɟɦ ɪɚɡɞɟɥɟ ɦɵ ɜɵɜɟɥɢ ɭɪɚɜɧɟɧɢɹ ɦɚɤɪɨɫɤɨɩɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ ɢɡ
ɪɚɫɫɦɨɬɪɟɧɢɹ ɩɪɨɰɟɫɫɚ ɦɢɤɪɨɫɤɨɩɢɱɟɫɤɨɝɨ. Ɉɛɫɭɠɞɚɹ ɦɚɫɬɟɪ-ɭɪɚɜɧɟɧɢɟ, ɦɵ
ɜɵɹɫɧɢɥɢ, ɱɬɨ ɩɨɥɧɨɫɬɶɸ ɩɪɟɧɟɛɪɟɱɶ ɬɚɤɢɦɢ ɦɢɤɪɨɫɤɨɩɢɱɟɫɤɢɦɢ ɩɪɨɰɟɫɫɚɦɢ ɧɟɥɶɡɹ,
ɩɨɫɤɨɥɶɤɭ ɨɧɢ ɩɨɪɨɠɞɚɸɬ ɮɥɭɤɬɭɢɪɭɸɳɢɟ ɜɵɧɭɠɞɚɸɳɢɟ ɫɢɥɵ, ɫɩɨɫɨɛɧɵɟ ɭɜɟɫɬɢ
ɫɢɫɬɟɦɭ ɩɪɨɱɶ ɨɬ ɪɚɜɧɨɜɟɫɢɹ. ȼ ɷɬɨɦ ɪɚɡɞɟɥɟ ɦɵ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɢɡɭɱɢɦ ɞɢɧɚɦɢɤɭ
ɫɨɜɨɤɭɩɧɵɯ ɩɟɪɟɦɟɧɧɵɯ, ɪɚɫɫɦɚɬɪɢɜɚɹ ɦɢɤɪɨɫɤɨɩɢɱɟɫɤɢɟ

ɮɥɭɤɬɭɚɰɢɨɧɧɵɟ ɫɢɥɵ ɤɚɤ ɢɫɬɨɱɧɢɤ ɲɭɦɚ, ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɣ ɨɩɪɟɞɟɥɟɧɧɵɦ
ɬɪɟɛɨɜɚɧɢɹɦ.
ɗɜɨɥɸɰɢɹ ɜɨ ɜɪɟɦɟɧɢ ɡɚɜɢɫɢɬ ɨɬ ɩɪɢɱɢɧ, ɩɪɟɞɫɤɚɡɚɬɶ ɤɨɬɨɪɵɟ ɫ ɚɛɫɨɥɸɬɧɨɣ
ɬɨɱɧɨɫɬɶɸ ɧɟɜɨɡɦɨɠɧɨ. Ɉɛɵɱɧɨ ɩɨɞɨɛɧɵɟ ɩɪɢɱɢɧɵ ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɤɚɤ
ɮɥɭɤɬɭɢɪɭɸɳɢɟ ɫɢɥɵ F(t). Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɞɢɧɚɦɢɤɭ ɫɢɫɬɟɦɵ (3.1.2) ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ
ɤɚɤ
ɝɞɟ F(t) ɡɚɞɚɧɨ. ɗɬɚ ɮɨɪɦɚ ɭɱɟɬɚ ɮɥɭɤɬɭɢɪɭɸɳɢɯ ɫɢɥ ɜ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɨɦ
ɭɪɚɜɧɟɧɢɢ ɧɚɡɵɜɚɟɬɫɹ ɚɞɞɢɬɢɜɧɵɦ ɲɭɦɨɦ. ɍɱɟɬ ɫɥɭɱɚɣɧɨɝɨ ɜɨɡɞɟɣɫɬɜɢɹ
ɨɤɪɭɠɚɸɳɟɣ ɫɪɟɞɵ ɦɨɠɧɨ ɩɪɨɜɟɫɬɢ ɜ ɞɪɭɝɨɣ ɮɨɪɦɟ. ɇɚɩɪɢɦɟɪ, ɟɫɥɢ ɪɨɫɬ ɩɨɩɭɥɹɰɢɢ
ɢɦɟɟɬ ɮɥɭɤɬɭɚɰɢɢ, ɬɨ ɞɢɧɚɦɢɤɚ ɩɨɩɭɥɹɰɢɢ ɡɚɞɚɟɬɫɹ ɜɵɪɚɠɟɧɢɟɦ
ɝɞɟ ȇ — ɱɢɫɥɟɧɧɨɫɬɶ ɩɨɩɭɥɹɰɢɢ, a(t) — ɫɥɭɱɚɣɧɚɹ ɫɤɨɪɨɫɬɶ ɪɨɫɬɚ. ɗɬɨɬ ɬɢɩ
ɮɥɭɤɬɭɚɰɢɢ ɧɚɡɵɜɚɟɬɫɹ ɦɭɥɶɬɢɩɥɢɤɚɬɢɜɧɵɦ ɲɭɦɨɦ. ȼ ɷɬɨɦ ɪɚɡɞɟɥɟ ɧɚɫ ɛɭɞɟɬ
ɢɧɬɟɪɟɫɨɜɚɬɶ ɜɥɢɹɧɢɟ ɚɞɞɢɬɢɜɧɨɝɨ ɲɭɦɚ ɧɚ ɞɢɧɚɦɢɤɭ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ
ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɯ ɭɪɚɜɧɟɧɢɣ dx/dt = f(x) ɜɛɥɢɡɢ ɧɟɭɫɬɨɣɱɢɜɵɯ ɨɫɨɛɵɯ ɬɨɱɟɤ.
ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɮɭɧɤɰɢɹ F ɫɪɚɜɧɢɬɟɥɶɧɨ ɦɚɥɚ ɜ ɬɨɦ ɫɦɵɫɥɟ, ɱɬɨ ɨɧɚ ɧɟ
ɢɡɦɟɧɹɟɬ ɡɚɦɟɬɧɨ ɯɚɪɚɤɬɟɪ ɞɜɢɠɟɧɢɹ. ɗɬɨ
ɨɡɧɚɱɚɟɬ, ɱɬɨ ɧɟɭɫɬɨɣɱɢɜɨɫɬɶ ɜɧɟɫɟɧɚ ɜ
ɫɢɫɬɟɦɭ ɧɟ ɫɨ ɫɬɨɪɨɧɵ ɮɥɭɤɬɭɢɪɭɸɳɢɯ ɱɚɫɬɟɣ, ɚ ɫɨ ɫɬɨɪɨɧɵ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɣ
ɱɚɫɬɢ f(x).
Ɍɢɩɢɱɧɵɦ ɩɪɢɦɟɪɨɦ ɭɪɚɜɧɟɧɢɹ ɬɢɩɚ (7.5.1) ɹɜɥɹɟɬɫɹ ɭɪɚɜɧɟɧɢɟ Ʌɚɧɠɟɜɟɧɚ ɞɥɹ
ɛɪɨɭɧɨɜɫɤɨɝɨ ɞɜɢɠɟɧɢɹ
ɝɞɟ x
i
, ɢ ɪ
i
— ɩɨɥɨɠɟɧɢɟ ɢ ɦɨɦɟɧɬ ɞɜɢɠɟɧɢɹ «ɛɪɨɭɧɨɜɫɤɨɣ» ɱɚɫɬɢɰɵ, ɜɡɜɟɲɟɧɧɨɣ
ɜ ɝɚɡɟ. ɋɢɥɚ, ɞɟɣɫɬɜɭɸɳɚɹ ɧɚ ɛɪɨɭɧɨɜɫɤɭɸ ɱɚɫɬɢɰɭ, ɪɚɫɩɚɞɚɟɬɫɹ ɧɚ ɫɢɫɬɟɦɚɬɢɱɟɫɤɭɸ
ɱɚɫɬɶ rɪ
i
ɢ «ɫɥɭɱɚɣɧɭɸ» ɮɥɭɤɬɭɢɪɭɸɳɭɸ ɤɨɦɩɨɧɟɧɬɭ F
i
. ȿɫɥɢ ɩɪɟɧɟɛɪɟɱɶ
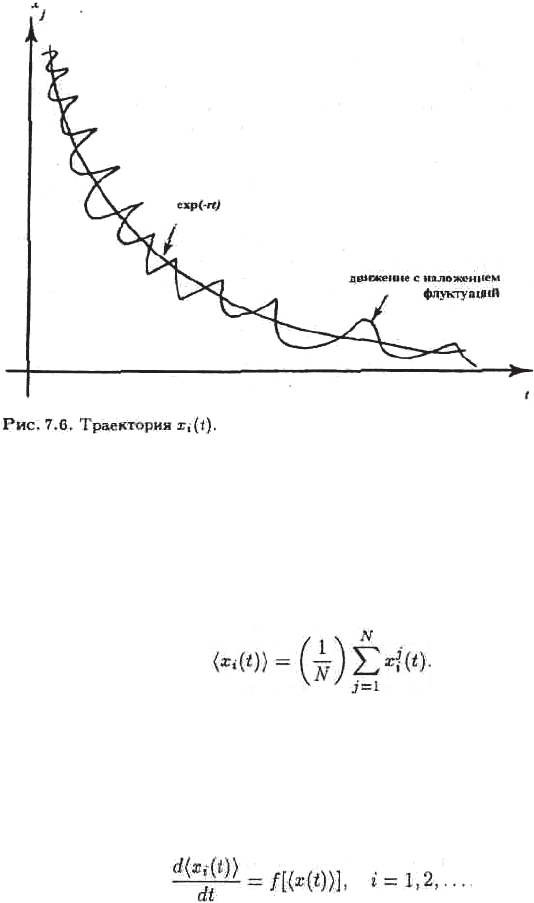
ɮɥɭɤɬɭɚɰɢɹɦɢ, Ⱦɜɢɠɟɧɢɟ ɛɪɨɭɧɨɜɫɤɨɣ ɱɚɫɬɢɰɵ ɞɨɥɠɧɨ ɡɚɬɭɯɚɬɶ ɞɨ ɫɨɫɬɨɹɧɢɹ ɩɨɥ-
ɧɨɝɨ ɩɨɤɨɹɬ ȼɥɢɹɧɢɟ ɮɥɭɤɬɭɚɰɢɢ ɦɨɠɟɬ ɩɪɢɜɟɫɬɢ ɤ ɧɟɩɪɟɤɪɚɳɚɸɳɟɦɭɫɹ
ɧɟɪɟɝɭɥɹɪɧɨɦɭ ɞɜɢɠɟɧɢɸ ɱɚɫɬɢɰɵ (ɪɢɫ. 7.6).
ɑɬɨɛɵ ɩɪɨɞɨɥɠɢɬɶ ɢɡɭɱɟɧɢɟ ɜɥɢɹɧɢɹ ɮɥɭɤɬɭɚɰɢɢ, ɜɜɟɞɟɦ ɩɨɧɹɬɢɟ ɬɚɤ
ɧɚɡɵɜɚɟɦɨɝɨ ɚɧɫɚɦɛɥɹ: ɪɚɫɫɦɨɬɪɢɦ ɚɧɫɚɦɛɥɶ ɦɚɤɪɨɫɢɫɬɟɦ,
ɢɦɟɸɳɢɯ ɨɞɢɧɚɤɨɜɵɣ ɫɨɫɬɚɜ ɢ ɨɩɢɫɵɜɚɟɦɵɯ ɨɞɧɢɦ ɢ ɬɟɦ ɠɟ ɦɧɨɠɟɫɬɜɨɦ
ɦɚɤɪɨɩɟɪɟɦɟɧɧɵɯ x
i
. Ʉɚɠɞɵɣ ɟɝɨ ɱɥɟɧ ɨɛɨɡɧɚɱɢɦ ɛɭɤɜɨɣ j. Ɋɚɫɫɦɨɬɪɢɦ ɫɥɭɱɚɣ, ɤɨɝɞɚ
ɤɚɠɞɵɣ ɱɥɟɧ ɩɨɞɜɟɪɝɚɟɬɫɹ ɜɨɡɞɟɣɫɬɜɢɸ ɪɚɡɥɢɱɧɵɯ ɦɢɤɪɨɫɤɨɩɢɱɟɫɤɢɯ ɮɥɭɤɬɭɚɰɢɢ F
i
.
Ɇɨɠɧɨ ɨɠɢɞɚɬɶ, ɱɬɨ ɞɥɹ ɪɚɡɧɵɯ ɱɥɟɧɨɜ ɚɧɫɚɦɛɥɹ ɦɵ ɛɭɞɟɦ ɧɚɛɥɸɞɚɬɶ ɪɚɡɥɢɱɧɵɟ
ɬɪɚɟɤɬɨɪɢɢ
j
i
x (t), ɞɚɠɟ ɟɫɥɢ ɡɧɚɱɟɧɢɹ ɩɟɪɟɦɟɧɧɵɯ ɜ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɹɯ
j
i
x (0) ɛɭɞɭɬ
ɨɞɧɢɦɢ ɢ ɬɟɦɢ ɠɟ. ɉɭɫɬɶ ¢x
i
(t)² ɨɛɨɡɧɚɱɚɟɬ ɫɪɟɞɧɸɸ ɩɨ ɚɧɫɚɦɛɥɸ ɜɟɥɢɱɢɧɭ
Ɏɥɭɤɬɭɚɰɢɢ ɦɨɠɧɨ ɨɩɪɟɞɟɥɹɬɶ ɪɚɡɧɵɦɢ ɫɩɨɫɨɛɚɦɢ. Ɇɵ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ
ɞɥɹ ɜɫɟɯ i ɢɦɟɟɬ ɦɟɫɬɨ ¢F
i
(t)²=0, ɯɨɬɹ ɢɯ ɤɨɜɚɪɢɚɰɢɢ ɧɟ ɪɚɜɧɵ ɬɨɠɞɟɫɬɜɟɧɧɨ ɧɭɥɸ.
Ɇɵ ɦɨɠɟɦ ɩɨɥɭɱɢɬɶ ɞɜɚ ɫɬɪɭɤɬɭɪɧɨ ɪɚɡɥɢɱɧɵɯ ɫɥɭɱɚɹ:
(i) ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɪɟɲɟɧɢɹ ɞɥɹ ɤɚɠɞɨɝɨ
j
i
x (t) ɩɪɢ ɨɞɧɨɦ ɢ ɬɨɦ ɠɟ ɧɚɱɚɥɶɧɨɦ
ɭɫɥɨɜɢɢ ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɨɬɤɥɨɧɹɸɬɫɹ ɨɬ ɫɜɨɢɯ ɫɪɟɞɧɢɯ ɡɧɚɱɟɧɢɣ ¢x
i
(t)². ȼ ɷɬɨɦ ɫɥɭɱɚɟ
ɦɵ ɩɨɥɭɱɢɦ ɫɥɟɞɭɸɳɢɟ ɩɪɢɛɥɢɠɟɧɧɵɟ ɭɪɚɜɧɟɧɢɹ ɞɥɹ ¢x
i
(t)²
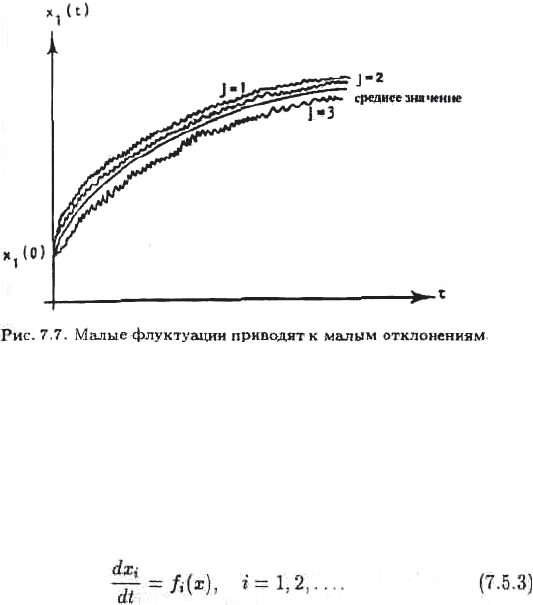
ɗɬɨ ɫɢɫɬɟɦɚ ɚɜɬɨɧɨɦɧɵɯ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɯ ɭɪɚɜɧɟɧɢɣ. ȿɟ ɪɟɲɟɧɢɟ ɨɱɟɧɶ
ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɨɬɤɥɨɧɹɟɬɫɹ ɨɬ ɫɚɦɨɣ ɬɪɚɟɤɬɨɪɢɢ
j
i
x . ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɦɚɤɪɨɩɟɪɟɦɟɧɧɵɟ
j
i
x (t) ɩɪɢɛɥɢɠɟɧɧɨ ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɡɚɦɤɧɭɬɨɣ ɚɜɬɨɧɨɦɧɨɣ ɩɨɞɫɢɫɬɟɦɟ ɭɪɚɜɧɟɧɢɣ
ɞɢɧɚɦɢɤɢ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɛɵɫɬɪɨ ɮɥɭɤɬɭɢɪɭɸɳɢɟ ɫɥɭɱɚɣɧɵɟ ɫɢɥɵ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ
ɦɢɤɪɨɩɟɪɟɦɟɧɧɵɟ, ɩɪɢɜɨɞɹɬ ɥɢɲɶ ɤ ɦɚɥɵɦ ɨɬɤɥɨɧɟɧɢɹɦ ɦɚɤɪɨɩɟɪɟɦɟɧɧɵɯ ɨɬ
ɝɥɚɞɤɨɣ ɤɪɢɜɨɣ ɫɪɟɞɧɟɝɨ ɩɨ ɚɧɫɚɦɛɥɸ (ɫɦ. ɪɢɫ. 7.7).
(ii) Ɋɚɫɫɦɨɬɪɢɦ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɟ ɭɪɚɜɧɟɧɢɟ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɟ ɭɪɚɜɧɟɧɢɸ
(7.5.1),
Ȼɨɥɶɲɨɟ ɱɢɫɥɨ ɩɪɢɦɟɪɨɜ ɢɡ ɩɪɟɞɵɞɭɳɢɯ ɝɥɚɜ ɝɨɜɨɪɢɬ ɨ ɬɨɦ, ɱɬɨ ɜ ɬɚɤɨɣ ɫɢɫɬɟɦɟ
ɦɨɝɭɬ ɜɨɡɧɢɤɧɭɬɶ ɛɢɮɭɪɤɚɰɢɢ. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ (7.5.1), ɫɬɚɪɬɭɹ ɜ
ɨɤɪɟɫɬɧɨɫɬɢ ɨɫɨɛɨɣ ɬɨɱɤɢ ɫɨ ɫɥɟɝɤɚ ɨɬɥɢɱɧɵɦɢ ɧɚɱɚɥɶɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ x
i
(0), ɦɨɝɭɬ
ɢɦɟɬɶ ɫɨɜɟɪɲɟɧɧɨ ɪɚɡɥɢɱɧɵɟ ɬɪɚɟɤɬɨɪɢɢ x
i
(t). Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɞɨɛɚɜɥɟɧɢɟ
ɮɥɭɤɬɭɚɰɢɢ ɜ ɬɚɤɭɸ ɫɢɫɬɟɦɭ ɦɨɠɟɬ ɩɪɢɜɟɫɬɢ ɤ ɬɪɚɟɤɬɨɪɢɹɦ, ɩɨɥɧɨɫɬɶɸ ɨɬɥɢɱɧɵɦ ɨɬ
ɬɪɚɟɤɬɨɪɢɣ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɝɨ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɝɨ ɭɪɚɜɧɟɧɢɹ. ɂɧɵɦɢ ɫɥɨɜɚɦɢ,
ɛɟɫɤɨɧɟɱɧɨ ɦɚɥɚɹ ɪɚɡɧɢɰɚ ɜ ɤɚɤɢɯ-ɥɢɛɨ «ɩɪɢɱɢɧɚɯ» ɦɨɠɟɬ ɩɪɢɜɟɫɬɢ ɤ ɨɱɟɧɶ ɛɨɥɶɲɨɣ
ɪɚɡɧɢɰɟ ɜ «ɩɨɫɥɟɞɫɬɜɢɹɯ». ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɢɧɞɢɜɢɞɭɚɥɶɧɚɹ ɬɪɚɟɤɬɨɪɢɹ
j
i
x ɦɨɠɟɬ
ɡɧɚɱɢɬɟɥɶɧɨ ɨɬɤɥɨɧɹɬɶɫɹ ɨɬ ɫɪɟɞɧɟɣ ɜɟɥɢɱɢɧɵ ¢x
i
(t)². ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɭɫɪɟɞɧɟɧɧɵɟ
ɭɪɚɜɧɟɧɢɹ ɞɢɧɚɦɢɤɢ ɧɟ ɝɨɞɹɬɫɹ ɞɥɹ ɨɩɢɫɚɧɢɹ ɷɜɨɥɸɰɢɢ ɫɢɫɬɟɦɵ (ɫɦ. ɪɢɫ. 7.8).
Ɋɚɫɫɦɨɬɪɢɦ ɩɪɨɫɬɵɟ ɦɨɞɟɥɢ «ɯɢɳɧɢɤ-ɠɟɪɬɜɚ» ɜ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ ɭɫɥɨɜɢɹɯ
ɨɤɪɭɠɚɸɳɟɣ ɫɪɟɞɵ. Ʉɥɚɫɫ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɯ ɦɨɞɟɥɟɣ
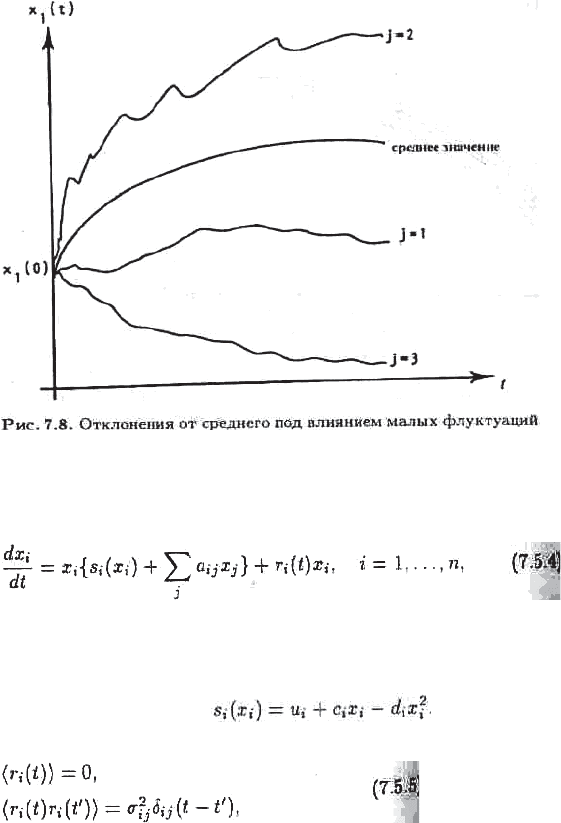
ɬɚɤɨɜ:
ɝɞɟ x
i
ɩɪɟɞɫɬɚɜɥɹɟɬ ɩɥɨɬɧɨɫɬɶ i-ɨɝɨ ɜɢɞɚ ɩɨɩɭɥɹɰɢɢ, Į
ij
— ɜɧɟɲɧɢɟ ɤɨɧɫɬɚɧɬɵ
Ʌɨɬɤɢ-ȼɨɥɶɬɟɪɪɚ, a s
i
(x
i
) ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɜɧɭɬɪɢɜɢɞɨɜɵɦ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹɦ
19
.
ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɟɫɥɢ i — ɯɢɳɧɢɤ, ɬɨ s
i
(x
i
) = u
i
(ɦɚɥɶɬɭɡɢɚɧɫɤɢɣ ɡɚɤɨɧ ɪɨɫɬɚ); ɟɫɥɢ
ɠɟ i — ɠɟɪɬɜɚ, ɬɨ
ȼɟɥɢɱɢɧɵ r
i
(t) ɜ (7.5.4) ɹɜɥɹɸɬɫɹ ɫɥɭɱɚɣɧɵɦɢ ɩɟɪɟɦɟɧɧɵɦɢ, ɜɨɡɞɟɣɫɬɜɭɸɳɢɦɢ ɧɚ
ɫɪɟɞɧɢɟ ɤɨɷɮɮɢɰɢɟɧɬɵ u
i
ɩɪɢ ɧɚɥɢɱɢɢ ɧɟɩɪɟɞɫɤɚɡɭɟɦɵɯ ɫɨɛɵɬɢɣ, ɬɚɤ ɱɬɨ
ɝɞɟ ¢.² ɨɡɧɚɱɚɟɬ ɫɪɟɞɧɟɟ ɩɨ ɚɧɫɚɦɛɥɸ. Ɇɵ ɩɪɟɞɩɨɥɚɝɚɟɦ, ɱɬɨ ɜɟɥɢɱɢɧɵ r
i
ɧɟ
ɤɨɪɪɟɥɢɪɭɸɬ ɞɪɭɝ ɫ ɞɪɭɝɨɦ ɢ ɢɦɟɸɬ ɞɟɥɶɬɚ-ɤɨɪɪɟɥɹɰɢɸ
19
Ɂɚɦɟɬɢɦ, ɱɬɨ ɡɞɟɫɶ ɧɢɱɟɝɨ ɧɟ ɝɨɜɨɪɢɬɫɹ ɨ ɡɧɚɤɚɯ ɩɚɪɚɦɟɬɪɨɜ. — ɉɪɢɦ. ɪɟɞ.

ɩɨ ɜɪɟɦɟɧɢ (į) ɫ ɩɨɫɬɨɹɧɧɨɣ ɞɢɫɩɟɪɫɢɟɣ (ı). Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɦɨɞɟɥɶ Ƚɭɞɜɢɧɚ ɢ ɟɟ
ɨɛɨɛɳɟɧɢɹ ɹɜɥɹɸɬɫɹ ɱɚɫɬɧɵɦɢ ɫɥɭɱɚɹɦɢ ɷɬɨɣ ɞɢɧɚɦɢɤɢ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɦɵ ɦɨɠɟɦ
ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ ɪɟɡɭɥɶɬɚɬɵ, ɩɨɥɭɱɟɧɧɵɟ ɞɥɹ ɷɬɢɯ ɞɢɧɚɦɢɱɟɫɤɢɯ ɫɢɫɬɟɦ ɜ ɬɟɪɦɢɧɚɯ
ɷɤɨɧɨɦɢɤɢ.
ɂɧɬɟɪɟɫɧɨ ɢɫɫɥɟɞɨɜɚɬɶ ɜɥɢɹɧɢɟ ɫɥɭɱɚɣɧɨɝɨ ɜɨɡɞɟɣɫɬɜɢɹ ɫɪɟɞɵ ɫ ɧɭɥɟɜɵɦ ɫɪɟɞɧɢɦ
ɧɚ ɩɨɜɟɞɟɧɢɟ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨɣ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɣ ɫɢɫɬɟɦɵ ɫ ɜɵɩɨɥɧɹɸɳɢɦɫɹ
ɬɨɠɞɟɫɬɜɨɦ
r
i
(i)=0. ɇɢɠɟ ɦɵ ɩɪɟɞɩɨɥɚɝɚɟɦ, ɱɬɨ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɟ ɭɪɚɜɧɟɧɢɹ,
ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɭɪɚɜɧɟɧɢɹɦ (7.5.4),
ɢɦɟɸɬ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ. ɏɨɪɨɲɨ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɜ ɦɨɞɟɥɹɯ ɷɬɨɝɨ ɬɢɩɚ ɩɪɟɞɟɥɶɧɵɟ
ɰɢɤɥɵ ɜɩɨɥɧɟ ɜɨɡɦɨɠɧɵ. ɉɪɢɦɟɧɹɹ ɬɟɨɪɟɦɭ ɏɨɩɮɚ ɨ ɛɢɮɭɪɤɚɰɢɹɯ, ɦɵ ɦɨɠɟɦ
ɩɨɥɭɱɢɬɶ ɬɨɱɧɵɟ ɭɫɥɨɜɢɹ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɩɪɟɞɟɥɶɧɵɯ ɰɢɤɥɨɜ.
ȼ ɥɢɬɟɪɚɬɭɪɟ ɢɦɟɸɬɫɹ ɧɟɤɨɬɨɪɵɟ ɜɟɫɶɦɚ ɢɧɬɟɪɟɫɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɨɬɧɨɫɢɬɟɥɶɧɨ
ɜɥɢɹɧɢɹ ɮɥɭɤɬɭɚɰɢɢ ɧɚ ɫɢɫɬɟɦɭ (7.5.4). ɇɚɩɪɢɦɟɪ, ɩɪɢɦɟɧɹɹ ɦɨɞɢɮɢɤɚɰɢɸ ɦɟɬɨɞɚ
ɨɫɪɟɞɧɟɧɢɹ, Ʌɢɧ ɢ Ʉɚɧ (1977) ɩɨɥɭɱɢɥɢ ɫɥɟɞɭɸɳɢɟ ɪɟɡɭɥɶɬɚɬɵ:
ɩɪɢ ɧɚɥɢɱɢɢ
ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ (ɚ) ɫ ɭɫɢɥɟɧɢɟɦ ɲɭɦɚ ɪɚɞɢɭɫ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ ɭɦɟɧɶɲɚɟɬɫɹ; (b)
ɟɫɥɢ ɞɢɫɩɟɪɫɢɹ ɲɭɦɚ ɛɨɥɶɲɟ ɪɚɞɢɭɫɚ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɝɨ ɰɢɤɥɚ, ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ
ɧɟ ɜɨɡɧɢɤɚɟɬ; ɢ (ɫ) ɞɢɫɩɟɪɫɢɹ ɭɝɥɨɜɨɣ ɩɟɪɟɦɟɧɧɨɣ ɥɢɧɟɣɧɨ ɪɚɫɬɟɬ ɫɨ ɜɪɟɦɟɧɟɦ.
ȼɵɜɨɞ (b) ɦɨɠɟɬ ɨɡɧɚɱɚɬɶ, ɱɬɨ ɟɫɥɢ ɲɭɦ ɨɬɧɨɫɢɬɟɥɶɧɨ ɜɟɥɢɤ, ɫɬɚɰɢɨɧɚɪɧɨɟ
ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɟɣ ɦɚɥɨɝɨ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɝɨ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ ɬɪɭɞɧɨ
ɨɬɥɢɱɢɬɶ ɨɬ ɪɚɫɩɪɟɞɟɥɟɧɢɹ
ɭɫɬɨɣɱɢɜɨɝɨ ɮɨɤɭɫɚ.
7.6. ȼɨɡɞɟɣɫɬɜɢɟ ɫɥɭɱɚɣɧɵɯ ɜɧɟɲɧɢɯ ɮɚɤɬɨɪɨɜ ɧɚ ɫɢɫɬɟɦɭ
ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɨɫɨɛɵɯ ɬɨɱɟɤ
Ɍɨɥɶɤɨ ɱɬɨ ɧɚ ɩɪɢɦɟɪɟ ɦɨɞɟɥɟɣ «ɯɢɳɧɢɤ-ɠɟɪɬɜɚ» ɦɵ ɩɨɤɚɡɚɥɢ, ɤɚɤ ɜɥɢɹɟɬ ɧɚ
ɩɨɜɟɞɟɧɢɟ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɣ ɫɢɫɬɟɦɵ, ɢɦɟɸɳɟɣ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ, ɜɧɟɲɧɢɣ ɲɭɦ ɫ
ɧɭɥɟɜɵɦ ɫɪɟɞɧɢɦ. ȼɦɟɫɬɟ ɫ ɬɟɦ ɜ ɝɥ. 5 ɧɚɦɢ ɭɫɬɚɧɨɜɥɟɧɨ ɫɭɳɟɫɬɜɨɜɚɧɢɟ
ɨɫɰɢɥɥɢɪɭɸɳɢɯ ɪɟɲɟɧɢɣ ɞɥɹ ɲɢɪɨɤɨɝɨ ɤɥɚɫɫɚ ɷɤɨɧɨɦɢɱɟɫɤɢɯ ɫɢɫɬɟɦ. ɉɨɫɤɨɥɶɤɭ
ɪɟɡɭɥɶɬɚɬɵ ɩɪɟɞɵɞɭɳɟɝɨ ɪɚɡɞɟɥɚ ɨɬɧɨɫɹɬɫɹ ɤ ɛɢɨɥɨɝɢɱɟɫɤɢɦ ɦɨɞɟɥɹɦ, ɜɚɠɧɨ
ɪɚɫɩɪɨɫɬɪɚɧɢɬɶ ɢɯ ɧɚ ɨɛɳɢɣ
ɫɥɭɱɚɣ.
Ɋɚɫɫɦɚɬɪɢɜɚɟɦɵɟ ɧɚɦɢ ɫɢɫɬɟɦɵ ɜɬɨɪɨɝɨ ɩɨɪɹɞɤɚ ɜ ɨɛɳɟɦ ɜɢɞɟ ɨɩɢɫɵɜɚɸɬɫɹ
ɭɪɚɜɧɟɧɢɹɦɢ ɬɢɩɚ
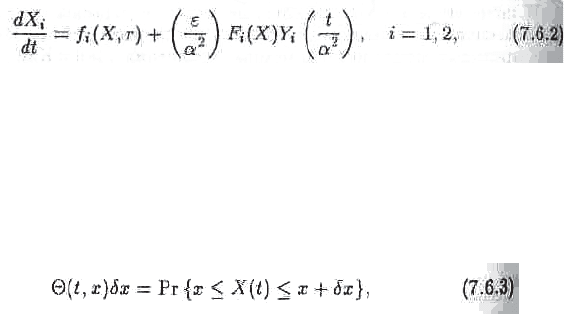
ɝɞɟ r — ɩɚɪɚɦɟɬɪ. ȼ ɧɟɤɨɬɨɪɵɯ ɫɥɭɱɚɹɯ ɬɚɤɚɹ ɫɢɫɬɟɦɚ ɦɨɠɟɬ ɢɦɟɬɶ ɧɟɫɤɨɥɶɤɨ
ɩɪɟɞɟɥɶɧɵɯ ɰɢɤɥɨɜ. ɋɢɫɬɟɦɚ ɩɨɥɧɨɫɬɶɸ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɚ. Ɏɥɭɤɬɭɚɰɢɢ ɧɟ
ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ.
ȼ ɪɚɛɨɬɟ Ɇɚɧɝɟɥɹ (1980) ɛɵɥɨ ɢɫɫɥɟɞɨɜɚɧɨ ɜɥɢɹɧɢɟ ɮɥɭɤɬɭɚɰɢɢ ɧɚ ɫɢɫɬɟɦɵ ɫ
ɨɞɧɢɦ ɢ ɧɟɫɤɨɥɶɤɢɦɢ ɩɪɟɞɟɥɶɧɵɦɢ ɰɢɤɥɚɦɢ. Ɉɧ ɪɚɫɫɦɚɬɪɢɜɚɥ ɱɟɬɵɪɟ ɬɢɩɚ
ɩɟɪɢɨɞɢɱɟɫɤɢɯ ɞɜɢɠɟɧɢɣ. ɂɦɟɧɧɨ: (1) ɧɟɩɨɞɜɢɠɧɵɣ ɭɫɬɨɣɱɢɜɵɣ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ,
ɨɯɜɚɬɵɜɚɸɳɢɣ ɬɨɱɤɭ ɧɟɭɫɬɨɣɱɢɜɨɝɨ ɮɨɤɭɫɚ (ɪɢɫ. 7.9ɚ
); (2) ɧɟɩɨɞɜɢɠɧɵɣ ɧɟɭɫɬɨɣ-
ɱɢɜɵɣ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ ɜɨɤɪɭɝ ɭɫɬɨɣɱɢɜɨɝɨ ɮɨɤɭɫɚ, ɡɚɤɥɸɱɟɧɧɨɝɨ ɜɧɭɬɪɢ
ɭɫɬɨɣɱɢɜɨɝɨ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ (ɪɢɫ. 7.9b); (3) ɡɚɞɚɱɢ ɨ ɛɢɮɭɪɤɚɰɢɹɯ ɏɨɩɮɚ ɢ (4)
«ɞɭɚɥɶɧɵɟ» ɛɢɮɭɪɤɚɰɢɢ, ɜ ɤɨɬɨɪɵɯ ɧɚɛɥɸɞɚɟɬɫɹ ɫɪɚɫɬɚɧɢɟ ɧɟɭɫɬɨɣɱɢɜɨɝɨ ɰɢɤɥɚ ɢ
ɭɫɬɨɣɱɢɜɨɝɨ ɮɨɤɭɫɚ (ɪɢɫ. 7.9ɫ). ȼɫɟ ɷɬɢ ɬɢɩɵ ɩɨɜɟɞɟɧɢɹ ɥɟɝɤɨ ɨɛɧɚɪɭɠɢɬɶ ɜ ɞɢɧɚɦɢ-
ɱɟɫɤɢɯ ɫɢɫɬɟɦɚɯ.
Ɇɚɧɝɟɥɶ ɭɱɟɥ ɲɭɦ ɜ ɭɪɚɜɧɟɧɢɹɯ (7.6.1) ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ
ɝɞɟ X
i
— ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɫɥɭɱɚɣɧɚɹ ɮɭɧɤɰɢɹ ɩɟɪɟɦɟɧɧɨɣ x
i
, ɚ Y — ɫɬɚɰɢɨɧɚɪɧɵɣ
ɫɥɭɱɚɣɧɵɣ ɩɪɨɰɟɫɫ ɫ ɧɭɥɟɜɵɦ ɫɪɟɞɧɢɦ. ɉɚɪɚɦɟɬɪ İ (0 < İ « 1) ɯɚɪɚɤɬɟɪɢɡɭɟɬ
ɢɧɬɟɧɫɢɜɧɨɫɬɶ ɮɥɭɤɬɭɚɰɢɢ. ȿɫɥɢ ɚ ɞɨɫɬɚɬɨɱɧɨ ɦɚɥɨ, ɫɥɭɱɚɣɧɵɣ ɩɪɨɰɟɫɫ X(t) ɫɯɨɞɢɬɫɹ
ɤ ɞɢɮɮɭɡɢɨɧɧɨɦɭ ɩɪɨɰɟɫɫɭ.
ɉɪɢ ɜɧɟɫɟɧɢɢ ɜ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɟ ɭɪɚɜɧɟɧɢɹ ɮɥɭɤɬɭɚɰɢɢ ɜɨɡɧɢɤɚɟɬ ɪɹɞ
ɜɨɩɪɨɫɨɜ, ɫɜɹɡɚɧɧɵɯ ɫ ɩɪɢɪɨɞɨɣ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɵɯ ɭɪɚɜɧɟɧɢɣ. ɇɚɩɪɢɦɟɪ, ɟɫɥɢ
ɬɪɚɟɤɬɨɪɢɹ ɫɢɫɬɟɦɵ ɜɫɟɝɞɚ ɫɬɪɟɦɢɬɫɹ ɤ ɭɫɬɨɣɱɢɜɨɦɭ ɩɪɟɞɟɥɶɧɨɦɭ
ɰɢɤɥɭ, ɤɚɤ ɧɚ ɪɢɫ.
7.9ɚ, ɜɚɠɧɨ ɡɧɚɬɶ, ɦɨɝɭɬ ɥɢ ɮɥɭɤɬɭɚɰɢɢ ɭɜɟɫɬɢ ɫɢɫɬɟɦɭ ɨɬ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ.
Ⱦɥɹ ɨɩɢɫɚɧɢɹ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɹ ɜɜɟɞɟɦ ɮɭɧɤɰɢɸ ɩɥɨɬɧɨɫɬɢ
ɜɟɪɨɹɬɧɨɫɬɢ Θ(x,t) ɫɥɭɱɚɣɧɨɝɨ ɩɪɨɰɟɫɫɚ X(t):
ɝɞɟ x ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɨɨɬɧɨɲɟɧɢɹɦɢ (7.6.1), a X(t) — ɫɨɨɬɧɨɲɟɧɢɹɦɢ (7.6.2). ȿɫɥɢ t
ĺ∞, ɬɨ ɩɥɨɬɧɨɫɬɶ ɜɟɪɨɹɬɧɨɫɬɢ Θ(x,t) ɭɫɬɪɟɦɢɬɫɹ ɤ ɪɚɜɧɨɜɟɫɧɨɣ ɢɥɢ ɫɬɚɰɢɨɧɚɪɧɨɣ
ɩɥɨɬɧɨɫɬɢ Θ(ɯ), ɤɨɬɨɪɚɹ ɨɡɧɚɱɚɟɬ ɜɨɡɦɨɠɧɨɫɬɶ ɧɚɯɨɠɞɟɧɢɹ ɩɪɨɰɟɫɫɚ ɜ ɢɧɬɟɪɜɚɥɟ (x, x
+ įx). ɉɥɨɬɧɨɫɬɢ ɜɟɪɨɹɬɧɨɫɬɢ Θ(t,x) ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɧɚɱɚɥɶɧɚɹ ɩɥɨɬɧɨɫɬɶ Θ(0,ȋ(0)),
ɤɨɬɨɪɚɹ ɯɚɪɚɤɬɟɪɢɡɭɟɬ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɏ(0) = x(0).
ȼ
ɫɥɭɱɚɟ ɛɢɮɭɪɤɚɰɢɢ ɏɨɩɮɚ ɧɚɫ ɢɧɬɟɪɟɫɭɟɬ ɩɥɨɬɧɨɫɬɶ ɜɟɪɨɹɬɧɨɫɬɢ ɫɥɭɱɚɣɧɨɝɨ
ɩɪɨɰɟɫɫɚ X(t) ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ
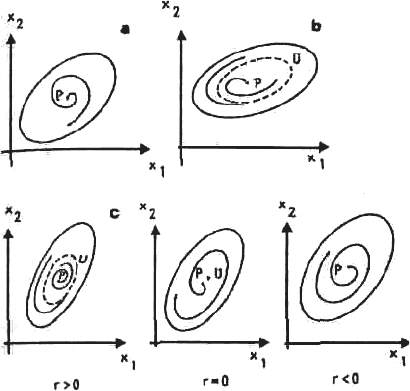
Ɋɢɫ. 7.9. (ɋɩɥɨɲɧɚɹ ɥɢɧɢɹ ɨɡɧɚɱɚɟɬ ɭɫɬɨɣɱɢɜɨɫɬɶ ɬɪɚɟɤɬɨɪɢɢ, ɩɭɧɤɬɢɪ — ɧɟɭɫɬɨɣɱɢɜɨɫɬɶ.)
ɩɚɪɚɦɟɬɪɚ r, ɤɨɬɨɪɭɸ ɛɭɞɟɦ ɨɛɨɡɧɚɱɚɬɶ Θ(t,x;r). Ɋɚɫɫɦɨɬɪɢɦ ɞɭɚɥɶɧɭɸ
ɛɢɮɭɪɤɚɰɢɨɧɧɭɸ ɫɢɫɬɟɦɭ ɏɨɩɮɚ (ɪɢɫ. 7.9ɫ). Ⱦɥɹ ɦɚɥɵɯ r ɮɚɡɨɜɚɹ ɬɨɱɤɚ ɩɨɤɢɧɟɬ
ɨɤɪɟɫɬɧɨɫɬɶ ɮɨɤɭɫɚ ȇ ɢɥɢ ɨɤɪɟɫɬɧɨɫɬɶ ɜɧɭɬɪɟɧɧɟɝɨ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ U ɢ ɛɭɞɟɬ
ɩɪɢɛɥɢɠɚɬɶɫɹ ɤɨ ɜɧɟɲɧɟɦɭ ɩɪɟɞɟɥɶɧɨɦɭ ɰɢɤɥɭ L ɫ ɧɟɤɨɬɨɪɨɣ ɜɟɪɨɹɬɧɨɫɬɶɸ. ɉɪɢ r=0
ɨɫɨɛɟɧɧɨɫɬɶ P/U ɛɭɞɟɬ ɩɪɨɹɜɥɹɬɶɫɹ ɜ ɨɱɟɧɶ ɦɟɞɥɟɧɧɨɦ ɞɟɬɟɪɦɢɧɢɪɨɜɚɧɧɨɦ
ɨɬɬɚɥɤɢɜɚɧɢɢ
ɨɬ Ɋ. ɉɭɫɬɶ L
*
—ɨɤɪɟɫɬɧɨɫɬɶ ɭɫɬɨɣɱɢɜɨɝɨ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ, ɢ ɩɭɫɬɶ
Ɍ(ɯ) = E{t: X(t}
∈
L
*
, X(s) ∉ L
*
, s < t°X(0) =
x}. (7.6.4)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, T (x) — ɜɪɟɦɹ ɩɪɟɞɩɨɥɚɝɚɟɦɨɝɨ ɩɨɩɚɞɚɧɢɹ ɜ ɨɛɥɚɫɬɶ L
*
ɩɪɢ
ɭɫɥɨɜɢɢ ɏ(0) = ɯ.
ɉɪɢ ɪɚɫɫɦɨɬɪɟɧɢɢ ɧɟɭɫɬɨɣɱɢɜɨɝɨ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ U, ɨɤɪɭɠɟɧɧɨɝɨ ɭɫɬɨɣɱɢɜɵɦ
ɩɪɟɞɟɥɶɧɵɦ ɰɢɤɥɨɦ ɤɚɤ ɧɚ ɪɢɫ. 7.10, ɧɚɱɚɥɶɧɨɟ ɩɨɥɨɠɟɧɢɟ ɮɚɡɨɜɨɣ ɬɨɱɤɢ ɹɜɥɹɟɬɫɹ
ɪɟɲɚɸɳɢɦ ɮɚɤɬɨɪɨɦ.
Ɏɚɡɨɜɚɹ ɬɨɱɤɚ, ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɩɪɢɧɚɞɥɟɠɚɳɚɹ ɨɤɪɟɫɬɧɨɫɬɢ U, c ɜɟɪɨɹɬɧɨɫɬɶɸ
ɟɞɢɧɢɰɚ ɩɨɤɢɞɚɟɬ ɷɬɭ ɨɤɪɟɫɬɧɨɫɬɶ. Ⱦɚɠɟ ɟɫɥɢ ɏ(0) ɧɚɯɨɞɢɬɫɹ ɧɚ ɫɚɦɨɦ ɩɪɟɞɟɥɶɧɨɦ
ɰɢɤɥɟ U, ɮɥɭɤɬɭɚɰɢɢ ɭɜɟɞɭɬ ɬɪɚɟɤɬɨɪɢɸ ɨɬ ɷɬɨɝɨ
ɩɨɥɨɠɟɧɢɹ. ɉɨɫɤɨɥɶɤɭ ɡɚɞɚɱɚ
ɨɩɪɟɞɟɥɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɢ ɬɨɝɨ, ɱɬɨ ɮɚɡɨɜɚɹ ɬɨɱɤɚ ɩɨɩɚɞɟɬ ɜ ɨɤɪɟɫɬɧɨɫɬɶ ɮɨɤɭɫɚ ȇ ɢɥɢ
ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ L ɫɥɢɲɤɨɦ ɫɥɨɠɧɚ, ɫɮɨɪɦɭɥɢɪɭɟɦ ɫɥɟɞɭɸɳɭɸ
