Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории
Подождите немного. Документ загружается.

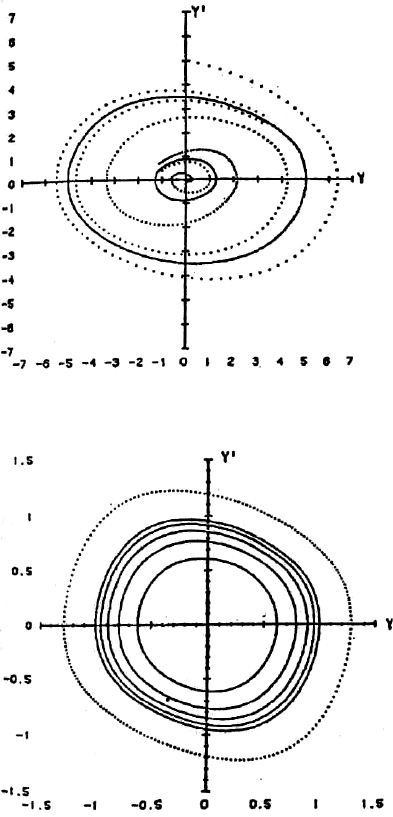
Ɋɢɫ. 8.8. ɍɫɬɨɣɱɢɜɵɣ ɢ ɧɟɭɫɬɨɣɱɢɜɵɣ ɩɪɟɞɟɥɶɧɵɟ ɰɢɤɥɵ.
Ɋɢɫ. 8.9. Ɉɫɰɢɥɥɹɰɢɢ ɧɚ ɪɚɡɧɵɯ ɪɚɫɫɬɨɹɧɢɹɯ (r = 1.5, 2, 2.5, 3, 3.5).
r. Ⱦɥɹ ɪɚɞɢɭɫɨɜ, ɦɟɧɶɲɢɯ ɟɞɢɧɢɰɵ, ɫɢɫɬɟɦɚ ɡɚɬɭɯɚɟɬ, ɢ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ ɧɟɬ. Ⱦɥɹ ɛɨɥɶɲɢɯ
ɪɚɞɢɭɫɨɜ ɜɨɡɧɢɤɚɸɬ ɩɪɟɞɟɥɶɧɵɟ ɐɢɤɥɵ ɜɨɡɪɚɫɬɚɸɳɢɯ ɚɦɩɥɢɬɭɞ, ɫɚɦɵɣ ɞɚɥɶɧɢɣ ɨɬ ɰɟɧɬɪɚ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɛɟɫɤɨɧɟɱɧɨɦɭ ɪɚɞɢɭɫɭ. ɏɨɬɹ ɚɦɩɥɢɬɭɞɵ ɰɢɤɥɨɜ ɜɨɡɪɚɫɬɚɸɬ
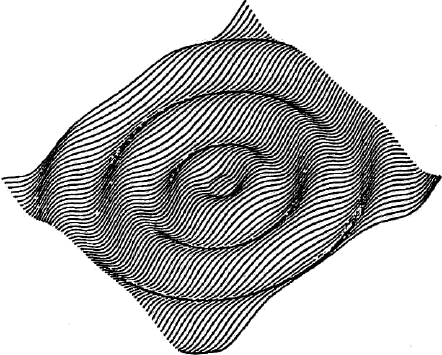
Ɋɢɫ. 8.10. Ⱥɫɢɦɩɬɨɬɢɱɟɫɤɨɟ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ.
ɫ ɪɚɫɫɬɨɹɧɢɟɦ ɨɬ ɧɚɱɚɥɚ ɤɨɨɪɞɢɧɚɬ, ɩɟɪɢɨɞ ɰɢɤɥɨɜ, ɩɨ-ɜɢɞɢɦɨɦɭ ɨɞɢɧɚɤɨɜ (ɉɭɭ, 1986).
Ⱥɫɢɦɩɬɨɬɢɱɟɫɤɨɟ ɪɟɲɟɧɢɟ ɩɟɪɜɨɝɨ ɩɪɢɛɥɢɠɟɧɢɹ ɬɚɤɠɟ ɩɨɫɬɪɨɟɧɨ ɉɭɭ. Ɋɟɲɟɧɢɟ
ɨɩɪɟɞɟɥɹɟɬ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɩɪɢ ɡɚɞɚɧɧɨɦ t. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɚɹ
ɤɨɨɪɞɢɧɚɬɚ ɪɚɫɫɦɚɬɪɢɜɚɟɬɫɹ ɤɚɤ ɛɢɮɭɪɤɚɰɢɨɧɧɵɣ ɩɚɪɚɦɟɬɪ ɜɪɟɦɟɧɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ.
ɉɨɜɟɞɟɧɢɟ ɚɫɢɦɩɬɨɬɢɱɟɫɤɢɯ ɪɟɲɟɧɢɣ ɜɢɞɧɨ ɢɡ ɪɢɫ. 8.10.
ɉɨɤɚɡɚɧɨ, ɱɬɨ ɜɜɟɞɟɧɢɟ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɣ ɡɚɜɢɫɢɦɨɫɬɢ
ɪɚɡɪɭɲɚɟɬ ɢɞɟɚɥɶɧɭɸ ɜɪɟɦɟɧɧɭɸ
ɩɟɪɢɨɞɢɱɧɨɫɬɶ ɢɫɯɨɞɧɨɣ ɦɨɞɟɥɢ ɢ ɩɪɢɜɨɞɢɬ ɤ ɡɚɦɟɧɟ ɩɪɨɫɬɨɝɨ ɝɚɪɦɨɧɢɱɟɫɤɨɝɨ ɞɜɢɠɟɧɢɹ ɧɚ
ɧɟɪɟɝɭɥɹɪɧɨɟ ɜɨ ɜɪɟɦɟɧɢ. ȼ ɷɬɨɦ ɨɬɧɨɲɟɧɢɢ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɚɹ ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɞɨɛɧɚ
ɞɟɣɫɬɜɢɸ ɪɚɫɩɪɟɞɟɥɟɧɧɨɣ ɫɢɫɬɟɦɵ ɫ ɡɚɩɚɡɞɵɜɚɧɢɟɦ.
8.4 ɉɪɨɫɬɪɚɧɫɬɜɟɧɧɚɹ ɞɢɮɮɭɡɢɹ
ɤɚɤ ɫɬɚɛɢɥɢɡɚɬɨɪ
ɉɪɟɞɵɞɭɳɢɟ ɦɨɞɟɥɢ ɛɵɥɢ ɩɨɫɬɪɨɟɧɵ ɜ ɪɚɦɤɚɯ ɩɨɞɯɨɞɚ, ɩɪɟɞɥɨɠɟɧɧɨɝɨ Ȼɟɤɦɚɧɨɦ ɢ ɉɭɭ.
Ⱥɜɬɨɪɨɦ ɷɬɨɣ ɤɧɢɝɢ ɧɟɞɚɜɧɨ ɩɪɟɞɥɨɠɟɧɚ ɧɟɫɤɨɥɶɤɨ ɞɪɭɝɚɹ ɦɨɞɟɥɶ ɝɨɪɨɞɚ, ɝɞɟ ɜ ɮɨɤɭɫɟ
ɜɧɢɦɚɧɢɹ ɧɚɯɨɞɢɬɫɹ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɧɚɫɟɥɟɧɢɹ ɢ ɧɟɤɨɬɨɪɵɯ Ⱦɪɭɝɢɯ
ɩɟɪɟɦɟɧɧɵɯ, ɯɚɪɚɤɬɟɪɢɡɭɸɳɢɯ ɝɨɪɨɞ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɷɤɨɧɨɦɢɱɟɫɤɚɹ ɞɟɹɬɟɥɶɧɨɫɬɶ
ɫɨɫɪɟɞɨɬɨɱɟɧɚ ɜ ɨɬɞɟɥɶɧɵɯ ɬɨɱɤɚɯ ɝɨɪɨɞɚ. ȼ ɨɫɬɚɜɲɟɣɫɹ ɱɚɫɬɢ ɝɥɚɜɵ ɦɵ ɪɚɫɫɦɨɬɪɢɦ ɪɹɞ
ɦɨɞɟɥɟɣ
ɜ ɪɚɦɤɚɯ ɬɚɤɨɝɨ ɩɨɞɯɨɞɚ.
ɇɚɫ ɢɧɬɟɪɟɫɭɟɬ ɦɨɞɟɥɢɪɨɜɚɧɢɟ ɩɨɜɟɞɟɧɢɹ ɞɨɦɨɜɥɚɞɟɥɶɰɟɜ ɜ

ɩɪɨɫɬɪɚɧɫɬɜɟ. ɏɨɪɨɲɨ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ ɢ ɫɨɰɢɨ-ɷɤɨɧɨɦɢɱɟɫɤɨɣ
ɞɟɹɬɟɥɶɧɨɫɬɢ ɬɹɝɨɬɟɸɬ ɤ ɚɝɪɟɝɚɰɢɢ ɢ ɪɟɝɢɨɧɚɥɢɡɚɰɢɢ. ɉɪɢɱɢɧɨɣ ɪɟɝɢɨɧɚɥɢɡɚɰɢɢ ɦɨɠɟɬ
ɫɥɭɠɢɬɶ ɧɚɥɢɱɢɟ «ɦɚɫɲɬɚɛɧɵɯ ɮɚɤɬɨɪɨɜ» ɞɥɹ ɥɸɞɟɣ ɢ ɢɯ ɚɤɬɢɜɧɨɫɬɢ. Ɋɟɡɭɥɶɬɚɬɨɦ ɬɚɤɢɯ
ɬɟɧɞɟɧɰɢɣ ɹɜɥɹɟɬɫɹ ɧɟɪɚɜɧɨɦɟɪɧɨɫɬɶ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ ɢ ɫɨɰɢɨ-ɷɤɨɧɨɦɢɱɟɫɤɨɣ
ɞɟɹɬɟɥɶɧɨɫɬɢ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ ɢ ɜɪɟɦɟɧɢ. ȼ ɷɬɨɦ ɪɚɡɞɟɥɟ ɩɪɢɜɨɞɢɬɫɹ ɦɨɞɟɥɶ, ɪɚɡɪɚɛɨɬɚɧɧɚɹ
Ɂɚɧɝɨɦ (1988ɫ) ɞɥɹ
ɭɱɟɬɚ ɷɮɮɟɤɬɨɜ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɣ ɞɢɮɮɭɡɢɢ ɩɪɢ ɮɨɪɦɢɪɨɜɚɧɢɢ
ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ.
Ɋɚɫɫɦɚɬɪɢɜɚɟɬɫɹ ɝɨɪɨɞɫɤɚɹ ɫɢɫɬɟɦɚ, ɫɨɫɬɨɹɳɚɹ ɢɡ ɬɪɟɯ ɱɚɫɬɟɣ: ɰɟɧɬɪɚɥɶɧɨɝɨ ɞɟɥɨɜɨɝɨ
ɪɚɣɨɧɚ (ɐȾɊ), ɩɪɢɥɟɝɚɸɳɟɣ ɨɛɥɚɫɬɢ ɢ ɝɪɚɧɢɰɵ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ. ɐȾɊ — ɷɬɨ ɦɟɫɬɨ,
ɝɞɟ ɪɟɚɥɢɡɭɟɬɫɹ ɛɨɥɶɲɚɹ ɱɚɫɬɶ ɫɨɰɢɨ-ɷɤɨɧɨɦɢɱɟɫɤɨɣ ɞɟɹɬɟɥɶɧɨɫɬɢ, ɧɨ ɫɨɰɢɨ-ɷɤɨɧɨɦɢɱɟɫɤɚɹ
ɞɟɹɬɟɥɶɧɨɫɬɶ ɦɨɠɟɬ ɢɦɟɬɶ ɦɟɫɬɨ ɢ ɜ ɞɪɭɝɢɯ ɱɚɫɬɹɯ ɝɨɪɨɞɫɤɨɣ ɫɢɫɬɟɦɵ. Ⱦɥɹ ɩɪɨɫɬɨɬɵ
ɦɵ
ɫɱɢɬɚɟɦ ɐȾɊ ɬɨɱɤɨɣ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɝɪɚɧɢɰɚ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɩɪɢɦɵɤɚɟɬ ɤ
ɨɛɥɚɫɬɢ ɫɟɥɶɫɤɨɯɨɡɹɣɫɬɜɟɧɧɨɝɨ ɡɟɦɥɟɩɨɥɶɡɨɜɚɧɢɹ. Ɇɟɠɞɭ ɐȾɊ ɢ ɝɪɚɧɢɰɟɣ ɥɟɠɢɬ ɨɛɥɚɫɬɶ,
ɧɚɡɵɜɚɟɦɚɹ ɩɪɢɥɟɝɚɸɳɢɦ ɩɪɨɫɬɪɚɧɫɬɜɨɦ, ɝɞɟ ɥɸɞɢ ɦɨɝɭɬ ɫɬɪɨɢɬɶ ɞɨɦɚ ɢ ɡɚɧɢɦɚɬɶɫɹ ɞɪɭɝɨɣ
ɫɨɰɢɨ-ɷɤɨɧɨɦɢɱɟɫɤɨɣ ɞɟɹɬɟɥɶɧɨɫɬɶɸ.
ɉɪɨɰɟɫɫ ɮɨɪɦɢɪɨɜɚɧɢɹ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɨɩɢɫɵɜɚɟɬɫɹ ɞɜɢɠɟɧɢɟɦ ɩɥɨɬɧɨɫɬɢ
ɧɚɫɟɥɟɧɢɹ ɢ ɡɟɦɟɥɶɧɨɣ ɪɟɧɬɵ ɜɨ ɜɪɟɦɟɧɢ ɢ ɩɪɨɫɬɪɚɧɫɬɜɟ. ȼɜɟɞɟɦ ɨɩɪɟɞɟɥɟɧɢɹ
:
x(r,t) — ɩɥɨɬɧɨɫɬɶ ɧɚɫɟɥɟɧɢɹ ɜ ɬɨɱɤɟ (r,t),
y(r,t) — ɡɟɦɟɥɶɧɚɹ ɪɟɧɬɚ ɜ ɬɨɱɤɟ (r,t),
ɝɞɟ r — ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɐȾɊ ɞɨ ɬɨɱɤɢ ɩɪɢɥɟɝɚɸɳɟɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ. Ʉɨɝɞɚ ɩɟɪɟɦɟɧɧɵɟ x(r,t) ɢ
y(r,t) ɧɟ ɡɚɜɢɫɹɬ ɨɬ r, ɦɵ ɝɨɜɨɪɢɦ, ɱɬɨ ɝɨɪɨɞɫɤɚɹ ɦɨɞɟɥɶ ɨɞɧɨɪɨɞɧɚ, ɜ ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ —
ɝɟɬɟɪɨɝɟɧɧɚ. ɋɨɝɥɚɫɧɨ Ⱦɟɧɞɪɢɧɨɫɭ ɢ Ɇɭɥɥɚɥɥɢ (1985), ɟɫɥɢ ɝɨɪɨɞɫɤɨɟ ɩɪɨɫɬɪɚɧɫɬɜɨ
ɞɨɫɬɚɬɨɱɧɨ ɦɚɥɨ, ɞɢɧɚɦɢɤɚ ɫɢɫɬɟɦɵ
ɦɨɠɟɬ ɛɵɬɶ ɨɩɢɫɚɧɚ ɦɨɞɟɥɶɸ «ɯɢɳɧɢɤ-ɠɟɪɬɜɚ», ɤɚɤ ɜ
ɪɚɡɞ. 3.5,
()
()
,yxx
dt
dy
,xyy
dt
dx
1
1
−β=
−α=
ɩɚɪɚɦɟɬɪɵ ɤɨɬɨɪɨɣ ɨɩɪɟɞɟɥɟɧɵ ɬɚɦ ɠɟ. Ɇɵ ɡɧɚɟɦ, ɱɬɨ ɪɟɲɟɧɢɟ ɷɬɨɣ ɫɢɫɬɟɦɵ ɨɫɰɢɥɥɹɬɨɪɧɨ
ɢ ɱɬɨ ɫɢɫɬɟɦɚ ɫɬɪɭɤɬɭɪɧɨ ɧɟɭɫɬɨɣɱɢɜɚ. ȼɨɡɧɢɤɚɟɬ ɜɨɩɪɨɫ, ɜɨɡɦɨɠɧɨ ɥɢ ɫɬɚɛɢɥɢɡɢɪɨɜɚɬɶ
ɫɢɫɬɟɦɭ ɫ ɩɨɦɨɳɶɸ ɞɢɮɮɭɡɢɨɧɧɵɯ ɷɮɮɟɤɬɨɜ.
ɉɪɢ ɧɟɤɨɬɨɪɵɯ ɩɪɟɞɩɨɥɨɠɟɧɢɹɯ ɨ «ɞɜɢɠɟɧɢɢ» ɡɟɦɟɥɶɧɨɣ ɪɟɧɬɵ
ɢ ɧɚɫɟɥɟɧɢɹ ɦɨɞɟɥɶ ɝɨɪɨɞɚ
ɬɢɩɚ «ɯɢɳɧɢɤ-ɠɟɪɬɜɚ» ɩɨɩɨɥɧɟɧɚ
(3.5.1)
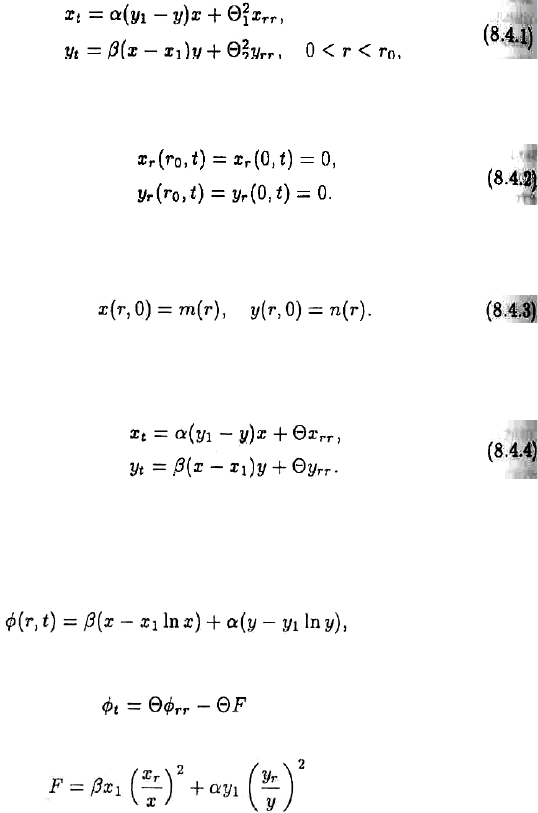
ɚɜɬɨɪɨɦ (Ɂɚɧɝ, 1988ɫ) ɞɢɮɮɭɡɢɨɧɧɵɦɢ ɱɥɟɧɚɦɢ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
ɝɞɟ r
0
— ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɐȾɊ ɞɨ ɝɨɪɨɞɫɤɨɣ ɝɪɚɧɢɰɵ, Θ
1
— ɩɚɪɚɦɟɬɪ, ɯɚɪɚɤɬɟɪɢɡɭɸɳɢɣ
ɫɬɪɟɦɥɟɧɢɟ ɢɡɛɟɠɚɬɶ ɫɤɨɩɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ, Θ
2
— «ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɜɨɞɢɦɨɫɬɢ ɪɟɧɬɵ».
Ƚɪɚɧɢɱɧɵɦ» ɭɫɥɨɜɢɹɦɢ ɹɜɥɹɸɬɫɹ 1
ɋɨɨɬɧɨɲɟɧɢɹ (8.4.2) ɨɡɧɚɱɚɸɬ, ɱɬɨ «ɩɨɬɨɤ» ɧɚɫɟɥɟɧɢɹ ɢ ɪɟɧɬɵ ɱɟɪɟɡ ɝɪɚɧɢɰɭ ɝɨɪɨɞɫɤɨɝɨ ɢ
ɫɟɥɶɫɤɨɯɨɡɹɣɫɬɜɟɧɧɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɨɬɫɭɬɫɬɜɭɟɬ. ɉɭɫɬɶ ɧɚɱɚɥɶɧɚɹ ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ
ɨɩɢɫɵɜɚɟɬɫɹ ɮɭɧɤɰɢɹɦɢ
ɉɨɥɧɚɹ ɦɨɞɟɥɶ ɝɨɪɨɞɚ ɫɨɫɬɨɢɬ ɢɡ (8.4.1)-(8.4.3). Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɷɬɚ ɫɢɫɬɟɦɚ ɢɦɟɟɬ
ɜɫɸɞɭ ɩɨɥɨɠɢɬɟɥɶɧɨɟ ɪɟɲɟɧɢɟ.
Ɋɚɫɫɦɨɬɪɢɦ ɫɩɟɪɜɚ ɫɥɭɱɚɣ
()
Θ=Θ=Θ
2
2
2
1
. ɍɪɚɜɧɟɧɢɹ (8.4.1) ɦɨɝɭɬ ɛɵɬɶ ɩɟɪɟɩɢɫɚɧɵ ɜ
ɜɢɞɟ
Ɍɟɨɪɟɦɚ 8.4.1. ȿɫɥɢ Θ
1
= Θ
2
, ɬɨ ɩɪɢ t →∞ ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ ɫɬɚɧɨɜɢɬɫɹ ɨɞɧɨɪɨɞɧɨɣ, ɬ.
ɟ. xr(r,t) = y
r
(r,t) = 0 ɩɪɢ t→∞.
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɦɨɠɧɨ ɧɚɣɬɢ ɜ ɪɚɛɨɬɟ Ɂɚɧɝɚ (1988ɫ). ɗɬɨɬ ɪɟɡɭɥɶɬɚɬ ɩɨɥɭɱɟɧ ɜɜɟɞɟɧɢɟɦ
ɮɭɧɤɰɢɢ
ɫ ɩɨɦɨɳɶɸ ɤɨɬɨɪɨɣ ɡɚɞɚɱɭ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɤɚɤ
ɫ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦɢ ɝɪɚɧɢɱɧɵɦɢ ɢ ɧɚɱɚɥɶɧɵɦɢ ɭɫɥɨɜɢɹɦɢ. Ɏɭɧɤɰɢɹ F ɡɚɜɢɫɢɬ ɨɬ x ɢ ɭ ɤɚɤ
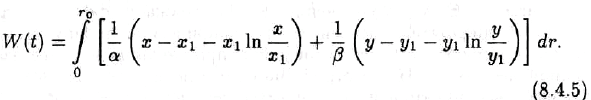
ɉɪɢɦɟɧɹɹ ɩɪɢɧɰɢɩ ɦɚɤɫɢɦɭɦɚ ɤ ɩɚɪɚɛɨɥɢɱɟɫɤɢɦ ɨɩɟɪɚɬɨɪɚɦ, ɦɵ ɦɨɠɟɦ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɩɪɢ t
→ ∞ ɢɦɟɟɬ ɦɟɫɬɨ F → 0 ɱɬɨ ɷɤɜɢɜɚɥɟɧɬɧɨ ɨɞɧɨɪɨɞɧɨɫɬɢ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ ɩɪɢ
ɞɨɫɬɚɬɨɱɧɨ ɛɨɥɶɲɢɯ t.
ɗɬɨɬ ɪɟɡɭɥɶɬɚɬ ɝɨɪɚɡɞɨ ɛɨɥɟɟ ɢɧɬɟɪɟɫɟɧ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɪɟɡɭɥɶɬɚɬɨɦ Ⱦɟɧɞɪɢɧɨɫɚ ɢ
Ɇɭɥɥɚɥɥɢ (1985). Ɉɧɢ ɧɟ ɪɚɫɫɦɚɬɪɢɜɚɥɢ ɜɥɢɹɧɢɟ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɣ ɞɢɮɮɭɡɢɢ ɧɚ ɝɨɪɨɞɫɤɭɸ
ɫɬɪɭɤɬɭɪɭ, ɩɪɟɞɩɨɥɨɠɢɜ, ɱɬɨ ɝɨɪɨɞɫɤɨɟ
ɩɪɨɫɬɪɚɧɫɬɜɨ ɨɱɟɧɶ ɦɚɥɨ. Ɍɟɨɪɟɦɚ 8.4.1 ɩɨɤɚɡɵɜɚɟɬ,
ɱɬɨ ɢɯ ɬɪɚɤɬɨɜɤɚ ɝɨɪɨɞɫɤɨɣ ɫɢɫɬɟɦɵ ɤɚɤ ɧɟɤɨɟɝɨ ɤɨɧɝɥɨɦɟɪɚɬɚ ɡɚɜɟɞɨɦɨ ɫɩɪɚɜɟɞɥɢɜɚ ɩɪɢ
ɫɬɪɨɝɨɦ ɜɵɩɨɥɧɟɧɢɢ ɭɫɥɨɜɢɹ Θ
1
= Θ
2
. ȼ ɷɬɨɦ ɫɥɭɱɚɟ, ɟɫɥɢ ɬɨɥɶɤɨ ɧɚɫ ɢɧɬɟɪɟɫɭɟɬ ɫɬɚɰɢ-
ɨɧɚɪɧɨɟ ɫɨɫɬɨɹɧɢɟ, ɜɜɟɞɟɧɢɟ ɞɢɮɮɭɡɢɨɧɧɵɯ ɷɮɮɟɤɬɨɜ ɧɟ ɩɨɜɥɢɹɟɬ ɧɚ ɩɨɜɟɞɟɧɢɟ ɫɢɫɬɟɦɵ,
ɯɨɬɹ ɦɨɠɟɬ ɩɨɜɥɢɹɬɶ ɧɚ ɟɟ ɭɫɬɨɣɱɢɜɨɫɬɶ.
Ɍɟɨɪɟɦɚ 8.4.2. ȿɫɥɢ șȚ ɢ ɜɡ ɧɟɧɭɥɟɜɵɟ, ɬɨ ɫɢɫɬɟɦɚ (8.4.1) ɧɟ ɢɦɟɟɬ ɧɟɨɞɧɨɪɨɞɧɵɯ
ɩɟɪɢɨɞɢɱɟɫɤɢɯ ɪɟɲɟɧɢɣ.
Ɋɚɫɫɦɨɬɪɢɦ ɮɭɧɤɰɢɸ
Ʌɟɝɤɨ ɩɪɨɜɟɪɢɬɶ, ɱɬɨ dW(t)/dt ≤ 0, ɬ. ɟ. ɮɭɧɤɰɢɹ W(t) — ɦɨɧɨɬɨɧɧɚɹ ɧɟɜɨɡɪɚɫɬɚɸɳɚɹ ɮɭɧɤɰɢɹ
ɜɪɟɦɟɧɢ. Ʉɪɨɦɟ ɬɨɝɨ, ɨɧɚ ɨɝɪɚɧɢɱɟɧɚ ɫɧɢɡɭ ɧɭɥɟɦ, ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɜɵɩɨɥɧɹɟɬɫɹ ɬɟɨɪɟɦɚ
8.4.2
20
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɜɟɞɟɧɢɟ ɝɟɨɝɪɚɮɢɱɟɫɤɢɯ ɮɚɤɬɨɪɨɜ ɧɚɪɭɲɢɥɨ ɜɨɡɦɨɠɧɨɫɬɶ ɧɟɨɞɧɨɪɨɞɧɵɯ
ɨɫɰɢɥɥɹɰɢɢ ɝɨɪɨɞɫɤɨɣ ɦɨɞɟɥɢ «ɯɢɳɧɢɤ-ɠɟɪɬɜɚ».
8.5 Ɋɚɡɞɟɥɟɧɢɟ ɢ ɫɨɫɭɳɟɫɬɜɨɜɚɧɢɟ
ɪɚɡɧɨɪɨɞɧɵɯ ɝɪɭɩɩ ɧɚɫɟɥɟɧɢɹ
ɝɨɪɨɞɚ
ɗɬɨɬ ɪɚɡɞɟɥ ɩɨɫɜɹɳɟɧ ɢɡɭɱɟɧɢɸ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɝɨ ɢ ɜɪɟɦɟɧɧɨɝɨ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɠɢɬɟɥɟɣ
ɝɨɪɨɞɚ. ɇɚɫɟɥɟɧɢɟ ɩɨɞɪɚɡɞɟɥɹɟɬɫɹ ɧɚ ɪɚɡɥɢɱɧɵɟ ɝɪɭɩɩɵ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɢɯ ɷɤɨɧɨɦɢɱɟɫɤɢɦɢ
ɢ ɢɧɞɢɜɢɞɭɚɥɶɧɵɦɢ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦɢ. ɇɚɫɟɥɟɧɢɟ ɦɨɠɧɨ ɤɥɚɫɫɢɮɢɰɢɪɨɜɚɬɶ ɩɨ ɰɜɟɬɭ ɤɨɠɢ
ɧɚ ɛɟɥɵɯ ɢ ɱɟɪɧɵɯ, ɩɨ ɭɪɨɜɧɸ ɞɨɯɨɞɚ ɢɥɢ ɨɛɪɚɡɨɜɚɧɢɹ. ȼ ɋɨɟɞɢɧɟɧɧɵɯ ɒɬɚɬɚɯ ɢ ɧɟɤɨɬɨɪɵɯ
ɞɪɭɝɢɯ ɫɬɪɚɧɚɯ ɫɨɫɭɳɟɫɬɜɨɜɚɧɢɟ ɝɪɭɩɩ ɧɚɫɟɥɟɧɢɹ, ɩɪɢɧɚɞɥɟɠɚɳɢɯ ɪɚɡɥɢɱɧɵɦ ɪɚɫɚɦ
,
20
Ɏɭɧɤɰɢɨɧɚɥ (8.4.5) ɩɨɡɜɨɥɹɟɬ ɩɟɪɟɧɟɫɬɢ ɪɟɡɭɥɶɬɚɬ ɬɟɨɪɟɦɵ 8.4.1 ɧɚ ɛɨɥɟɟ ɨɛɳɢɣ
ɫɥɭɱɚɣ ɬɟɨɪɟɦɵ 8.4.2. Ɂɚɦɟɬɢɦ, ɱɬɨ ɨɧ ɭɛɵɜɚɟɬ ɬɨɥɶɤɨ ɧɚ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨ ɧɟɨɞɧɨɪɨɞɧɵɯ
ɪɟɲɟɧɢɹɯ. Ɉɞɧɨɪɨɞɧɨɟ ɩɟɪɢɨɞɢɱɟɫɤɨɟ ɪɟɲɟɧɢɟ (3.5.1) ɍɞɨɜɥɟɬɜɨɪɹɟɬ ɫɢɫɬɟɦɟ (8.4.1). —
ɉɪɢɦ. ɪɟɞ.
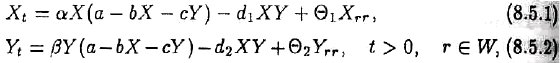
ɩɨɪɨɠɞɚɥɨ ɫɟɪɶɟɡɧɵɟ ɫɨɰɢɚɥɶɧɵɟ ɩɪɨɛɥɟɦɵ ɢ ɩɨɬɨɦɭ ɢɡɭɱɚɥɨɫɶ ɫ ɪɚɡɥɢɱɧɵɯ ɬɨɱɟɤ ɡɪɟɧɢɹ.
Ɇɵ ɪɚɫɫɦɨɬɪɢɦ ɞɥɹ ɩɪɨɫɬɨɬɵ ɬɨɥɶɤɨ ɞɜɟ ɝɪɭɩɩɵ, ɨɛɨɡɧɚɱɚɟɦɵɟ ɤɚɤ ɝɪɭɩɩɚ 1 ɢ ɝɪɭɩɩɚ 2.
ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɦɟɠɞɭ ɨɛɟɢɦɢ ɝɪɭɩɩɚɦɢ ɫɭɳɟɫɬɜɭɟɬ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɜ ɬɨɦ ɫɦɵɫɥɟ, ɱɬɨ
ɢɯ ɨɬɧɨɲɟɧɢɹ ɜɥɢɹɸɬ ɧɚ ɯɚɪɚɤɬɟɪ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ. Ɉɬɧɨɲɟɧɢɹ ɦɨɝɭɬ ɛɵɬɶ
ɞɪɭɠɟɥɸɛɧɵɦɢ; ɧɟɞɪɭɠɟɥɸɛɧɵɦɢ ɢ «ɧɟɣɬɪɚɥɶɧɵɦɢ». ɉɨɤɚɠɟɦ, ɱɬɨ ɪɚɡɞɟɥɟɧɢɟ
ɢ
ɫɨɫɭɳɟɫɬɜɨɜɚɧɢɟ ɡɚɜɢɫɢɬ ɨɬ ɷɬɢɯ ɨɬɧɨɲɟɧɢɣ. Ɉɛɨɡɧɚɱɢɦ ɩɥɨɬɧɨɫɬɢ ɧɚɫɟɥɟɧɢɹ ɷɬɢɯ ɝɪɭɩɩ
ɤɚɤ X(r,t) ɢ Y(r,t), ɝɞɟ r — ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɐȾɊ ɞɨ ɦɟɫɬɚ ɩɪɨɠɢɜɚɧɢɹ. Ɋɚɫɫɦɚɬɪɢɜɚɟɦɚɹ ɨɛɥɚɫɬɶ
ɝɟɨɝɪɚɮɢɱɟɫɤɢ ɩɨɞɨɛɧɚ ɨɛɥɚɫɬɢ ɢɡ ɩɪɟɞɵɞɭɳɟɝɨ ɪɚɡɞɟɥɚ.
Ⱦɚɥɟɟ ɜ ɷɬɨɦ ɪɚɡɞɟɥɟ ɫɥɟɞɭɟɦ ɪɚɛɨɬɟ ɚɜɬɨɪɚ (Ɂɚɧɝ, 1989ɫ). ɗɜɨɥɸɰɢɹ ɨɛɟɢɯ ɝɪɭɩɩ ɦɨɠɟɬ
ɛɵɬɶ ɨɩɢɫɚɧɚ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
ɝɞɟ Į, b, ɫ ɢ d
i
(i = 1,2) — ɩɨɫɬɨɹɧɧɵɟ, W — ɨɛɥɚɫɬɶ, ɩɪɢɦɵɤɚɸɳɚɹ ɤ ɐȾɊ.
ɋɥɚɝɚɟɦɨɟ Θ
1
X
rr
ɜ ɭɪɚɜɧɟɧɢɢ (8.5.1) ɨɬɪɚɠɚɟɬ ɷɮɮɟɤɬ ɝɟɨɝɪɚɮɢɱɟɫɤɨɣ ɞɢɮɮɭɡɢɢ
ɧɚɫɟɥɟɧɢɹ. Ƚɟɨɝɪɚɮɢɱɟɫɤɢɟ ɞɢɮɮɭɡɢɨɧɧɵɟ ɱɥɟɧɵ ɢɡɦɟɪɹɸɬ ɫɤɥɨɧɧɨɫɬɶ ɥɸɞɟɣ ɤ ɩɪɨɠɢɜɚɧɢɸ
ɜ ɦɟɧɟɟ ɡɚɫɟɥɟɧɧɨɣ ɦɟɫɬɧɨɫɬɢ. ɉɚɪɚɦɟɬɪ Θ
1
ɧɚ ɫɚɦɨɦ ɞɟɥɟ ɦɨɠɟɬ ɡɚɜɢɫɟɬɶ ɨɬ ɧɟɢɡɜɟɫɬɧɵɯ
ɮɭɧɤɰɢɣ ɢ ɧɟɡɚɜɢɫɢɦɵɯ ɩɟɪɟɦɟɧɧɵɯ — ɤɨɨɪɞɢɧɚɬɵ ɢ ɜɪɟɦɟɧɢ. ɑɥɟɧ αɏ(ɚ - bɏ - ɫY)
ɨɩɢɫɵɜɚɟɬ ɪɟɚɤɰɢɸ ɧɚɫɟɥɟɧɢɹ ɧɚ ɷɤɨɧɨɦɢɱɟɫɤɢɟ ɭɫɥɨɜɢɹ. Ɇɵ ɢɧɬɟɪɩɪɟɬɢɪɭɟɦ Į ɤɚɤ
«ɮɢɡɢɱɟɫɤɭɸ» ɜɦɟɫɬɢɦɨɫɬɶ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɜ ɬɨɱɤɟ ɝ. Ʉɨɝɞɚ ɩɚɪɚɦɟɬɪ Į ɩɨɫɬɨɹɧɟɧ
(ɤɨɧɫɬɚɧɬɚ), ɮɢɡɢɱɟɫɤɚɹ ɜɦɟɫɬɢɦɨɫɬɶ ɨɞɧɨɪɨɞɧɚ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ. ȿɫɥɢ ɩɪɟɞɩɨɥɨɠɢɬɶ
, ɱɬɨ (bɏ
+ cY) — ɤɨɥɢɱɟɫɬɜɟɧɧɚɹ ɦɟɪɚ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɡɚɧɢɦɚɟɦɨɝɨ ɨɛɟɢɦɢ ɝɪɭɩɩɚɦɢ, ɬɨ ɜɟɥɢɱɢɧɭ (ɚ -
bɏ - cY) ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɢɡɛɵɬɨɤ ɩɪɟɞɥɨɠɟɧɢɹ ɮɢɡɢɱɟɫɤɨɣ ɜɦɟɫɬɢɦɨɫɬɢ. Ʉɨɝɞɚ ɷɬɚ
ɜɟɥɢɱɢɧɚ ɜ ɧɟɤɨɬɨɪɨɣ ɬɨɱɤɟ ɫɬɚɧɨɜɢɬɫɹ ɛɨɥɶɲɟ ɧɭɥɹ, ɬɨ ɞɚɧɧɨɟ ɦɟɫɬɨ ɩɪɨɠɢɜɚɧɢɹ
ɨɤɚɡɵɜɚɟɬɫɹ ɛɨɥɟɟ ɩɪɢɜɥɟɤɚɬɟɥɶɧɵɦ ɞɥɹ ɧɚɫɟɥɟɧɢɹ. Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɤɨɝɞɚ ɨɧɚ ɪɚɜɧɚ ɧɭɥɸ, ɚ
ɱɥɟɧɵ —d
1
XY ɢ ɞɢɮɮɭɡɢɨɧɧɵɟ ɷɮɮɟɤɬɵ ɩɪɟɧɟɛɪɟɠɢɦɨ ɦɚɥɵ, ɦɢɝɪɚɰɢɹ ɧɚɫɟɥɟɧɢɹ
ɩɪɟɤɪɚɳɚɟɬɫɹ. Ɇɧɨɠɢɬɟɥɶ ɚɏ ɜ ɭɪɚɜɧɟɧɢɢ (8.5.1) — ɷɬɨ ɫɤɨɪɨɫɬɶ ɭɫɬɚɧɨɜɥɟɧɢɹ ɪɚɜɧɨɜɟɫɧɨɝɨ
ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ ɜ ɝɪɭɩɩɟ 1: ɟɫɥɢ ɩɥɨɬɧɨɫɬɶ ɧɚɫɟɥɟɧɢɹ ɜɵɫɨɤɚ, ɬɨ ɭɫɬɚɧɨɜɥɟɧɢɟ
ɪɚɜɧɨɜɟɫɢɹ ɡɚɦɟɞɥɟɧɨ, ɬɚɤ ɤɚɤ ɫɢɫɬɟɦɚ ɦɟɧɟɟ ɢɧɮɨɪɦɢɪɨɜɚɧɚ. ɑɥɟɧ — d
1
XY ɫɥɭɠɢɬ ɞɥɹ
ɢɡɦɟɪɟɧɢɹ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɝɪɭɩɩ. ɗɬɨɬ ɱɥɟɧ ɧɟ ɢɦɟɟɬ ɨɬɧɨɲɟɧɢɹ ɤ ɷɤɨɧɨɦɢɱɟɫɤɢɦ ɮɚɤɬɨɪɚɦ,
ɨɬɪɚɠɚɹ ɫɨɰɢɚɥɶɧɨɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ. Ʉɨɷɮɮɢɰɢɟɧɬ d
1
ɦɨɠɟɬ ɛɵɬɶ ɢ ɩɨɥɨɠɢɬɟɥɶɧɵɦ, ɢ
ɨɬɪɢɰɚɬɟɥɶɧɵɦ, ɢ ɧɭɥɟɜɵɦ. ȿɫɥɢ ɨɧ ɩɨɥɨɠɢɬɟɥɟɧ, ɝɪɭɩɩɟ 1 ɧɟ ɧɪɚɜɢɬɫɹ ɠɢɬɶ ɫ ɝɪɭɩɩɨɣ 2.
ȿɫɥɢ d
1
= 0, «ɪɚɫɨɜɵɟ» ɩɪɟɞɭɛɟɠɞɟɧɢɹ ɨɬɫɭɬɫɬɜɭɸɬ. ȿɫɥɢ d
1
ɨɬɪɢɰɚɬɟɥɟɧ, ɜɵɫɨɤɚɹ ɩɥɨɬɧɨɫɬɶ
ɝɪɭɩɩɵ 2 ɩɪɢɬɹɝɢɜɚɟɬ ɧɚɫɟɥɟɧɢɟ ɝɪɭɩɩɵ 1. ɇɚɩɪɢɦɟɪ,
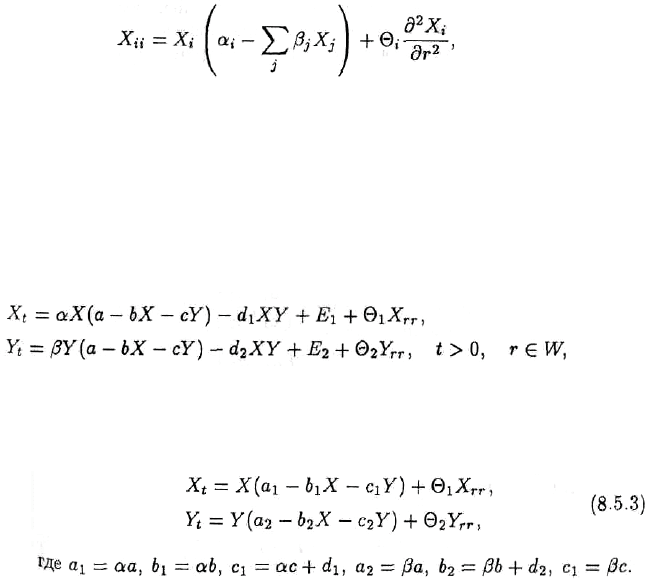
ɦɵ ɦɨɠɟɦ ɤɥɚɫɫɢɮɢɰɢɪɨɜɚɬɶ ɧɚɫɟɥɟɧɢɟ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɨɛɪɚɡɨɜɚɬɟɥɶɧɵɦ ɭɪɨɜɧɟɦ, ɢ ɦɟɧɟɟ
ɨɛɪɚɡɨɜɚɧɧɵɟ ɥɸɞɢ ɦɨɝɭɬ ɫɬɪɟɦɢɬɶɫɹ ɤ ɩɪɨɠɢɜɚɧɢɸ ɜ ɪɚɣɨɧɟ ɫ ɩɪɟɨɛɥɚɞɚɧɢɟɦ ɛɨɥɟɟ
ɜɵɫɨɤɨɨɛɪɚɡɨɜɚɧɧɵɯ.
ɉɨɞɨɛɧɵɦ ɠɟ ɨɛɪɚɡɨɦ ɦɨɠɧɨ ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ ɭɪɚɜɧɟɧɢɟ (8.5.2).
ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɷɬɭ ɫɢɫɬɟɦɭ ɦɨɠɧɨ ɪɚɫɲɢɪɢɬɶ, ɢ ɩɪɢɬɨɦ ɪɚɡɥɢɱɧɵɦɢ ɩɭɬɹɦɢ.
ɇɚɩɪɢɦɟɪ, ɦɵ ɦɨɠɟɦ ɪɚɡɛɢɬɶ ɧɚɫɟɥɟɧɢɟ ɧɚ N ɝɪɭɩɩ (N > 2). ɉɨ ɚɧɚɥɨɝɢɢ
ɫ ɧɚɲɟɣ ɛɚɡɨɜɨɣ
ɦɨɞɟɥɶɸ, ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɟ ɢ ɜɪɟɦɟɧɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɧɚɫɟɥɟɧɢɹ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɦɨɠɧɨ
ɡɚɩɢɫɚɬɶ ɜ ɨɛɳɟɦ ɜɢɞɟ ɤɚɤ
ɜɦɟɫɬɟ ɫ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦɢ ɧɚɱɚɥɶɧɵɦɢ ɢ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ. Ɂɚɬɟɦ ɦɨɠɧɨ ɢɫɫɥɟɞɨɜɚɬɶ
ɪɚɡɧɨɨɛɪɚɡɧɵɟ ɭɫɥɨɜɢɹ ɫɨɜɦɟɫɬɧɨɝɨ ɢ ɪɚɡɞɟɥɶɧɨɝɨ ɩɪɨɠɢɜɚɧɢɹ ɪɚɡɥɢɱɧɵɯ ɤɨɦɛɢɧɚɰɢɣ ɷɬɢɯ
ɝɪɭɩɩ.
Ɇɵ ɦɨɠɟɦ ɬɚɤɠɟ ɭɱɟɫɬɶ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɦɟɠɞɭ ɩɥɨɬɧɨɫɬɶɸ ɧɚɫɟɥɟɧɢɹ ɢ ɞɪɭɝɢɦɢ
ɩɟɪɟɦɟɧɧɵɦɢ, ɯɚɪɚɤɬɟɪɢɡɭɸɳɢɦɢ ɝɨɪɨɞ (ɝɪɚɞɨɨɛɪɚɡɭɸɳɢɦɢ ɩɟɪɟɦɟɧɧɵɦɢ), ɬɚɤɢɦɢ, ɤɚɤ
ɪɟɧɬɚ ɢ ɤɨɥɢɱɟɫɬɜɨ ɠɢɥɶɹ. ɉɪɢɦɟɪɨɦ ɬɚɤɨɝɨ ɩɨɞɯɨɞɚ ɫɥɭɠɢɬ ɦɨɞɟɥɶ ɢɡ ɩɪɟɞɵɞɭɳɟɝɨ
ɪɚɡɞɟɥɚ.
Ɇɨɠɧɨ
ɬɚɤɠɟ ɜɜɟɫɬɢ ɪɚɡɥɢɱɧɵɟ ɷɤɡɨɝɟɧɧɵɟ ɫɢɥɵ, ɜɨɡɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɫɬɪɭɤɬɭɪɭ ɝɨɪɨɞɚ.
ɇɚɩɪɢɦɟɪ, ɩɪɚɜɢɬɟɥɶɫɬɜɨ ɦɨɠɟɬ ɩɪɨɜɨɞɢɬɶ ɫɩɟɰɢɚɥɶɧɭɸ ɩɨɥɢɬɢɤɭ, ɱɬɨɛɵ ɝɚɪɚɧɬɢɪɨɜɚɬɶ
ɫɨɫɭɳɟɫɬɜɨɜɚɧɢɟ ɧɚɫɟɥɟɧɢɹ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɫɢɫɬɟɦɭ (8.5.1)-(8.5.2) ɦɨɠɧɨ ɨɛɨɛɳɢɬɶ ɤ
ɫɥɟɞɭɸɳɟɦɭ ɜɢɞɭ
ɝɞɟ E
1
(r,t) ɢ ȿ
2
(r,t) — ɷɤɡɨɝɟɧɧɵɟ «ɜɯɨɞɵ». ɇɚɩɪɢɦɟɪ, ȿ
1
ɦɨɠɟɬ ɨɡɧɚɱɚɬɶ ɢɦɦɢɝɪɚɰɢɸ ɝɪɭɩɩɵ
1 ɜ ɪɚɣɨɧɵ ɝɨɪɨɞɚ. ȿɫɥɢ ȿ
1
ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɪɚɫɫɬɨɹɧɢɹ, ɬɨ ɨɛɴɟɦ ɢɦɦɢɝɪɚɰɢɢ ɡɚɞɚɟɬɫɹ ɤɚɤ
ɜɟɥɢɱɢɧɚ ȿ
1
, ɭɦɧɨɠɟɧɧɚɹ ɧɚ ɪɚɡɦɟɪ ɝɨɪɨɞɫɤɨɝɨ ɪɚɣɨɧɚ.
Ⱦɥɹ ɩɪɨɫɬɨɬɵ ɦɵ ɨɝɪɚɧɢɱɢɦɫɹ ɧɚɢɛɨɥɟɟ ɥɟɝɤɢɦ ɫɥɭɱɚɟɦ (8.5.1)-(8.5.2). ɉɟɪɟɩɢɲɟɦ
ɦɨɞɟɥɶ ɤɚɤ

ɇɚɱɚɥɶɧɵɟ ɢ ɝɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ ɜɨɡɶɦɟɦ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɜ ɜɢɞɟ
ɝɞɟ n ɨɛɨɡɧɚɱɚɟɬ ɧɚɩɪɚɜɥɟɧɢɟ, ɧɨɪɦɚɥɶɧɨɟ ɤ ɝɪɚɧɢɰɟ ɢ ɨɪɢɟɧɬɢɪɨɜɚɧɧɨɟ ɜɨɜɧɟ, ∂W —
ɝɪɚɧɢɰɚ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɚ ɪ
i
ɢ q
i
(i = 1,2) — ɤɨɧɫɬɚɧɬɵ. Ƚɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ
ɨɩɪɟɞɟɥɹɸɬɫɹ ɬɟɦ, ɤɚɤ ɝɨɪɨɞɫɤɚɹ ɫɢɫɬɟɦɚ ɜɡɚɢɦɨɞɟɣɫɬɜɭɟɬ ɫ «ɜɧɟɲɧɢɦ ɦɢɪɨɦ». ȿɫɥɢ
ɫɱɢɬɚɬɶ, ɱɬɨ ∂ɏ/
∂
ɩ ɢ ∂Y/
∂
ɩ — ɦɢɝɪɚɰɢɹ ɧɚɫɟɥɟɧɢɹ, ɬɨ ɩɪɟɞɥɨɠɟɧɧɵɟ ɝɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ
ɨɡɧɚɱɚɸɬ, ɱɬɨ ɦɢɝɪɚɰɢɹ ɡɚɜɢɫɢɬ ɬɨɥɶɤɨ ɨɬ ɩɥɨɬɧɨɫɬɢ ɧɚɫɟɥɟɧɢɹ.
ȼ ɪɚɛɨɬɟ ɚɜɬɨɪɚ (Ɂɚɧɝ, 1989ɫ) ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɚɧɚɥɢɡɢɪɭɟɬɫɹ ɫɥɭɱɚɣ b = ɫ = 0 ɢ d
i
> 0 (i = 1,
2). ɗɬɨ ɡɧɚɱɢɬ, ɱɬɨ ɨɛɴɟɦ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɡɚɧɢɦɚɟɦɨɝɨ ɧɚɫɟɥɟɧɢɟɦ, ɧɟ ɜɥɢɹɟɬ ɧɚ ɦɢɝɪɚɰɢɸ, ɚ
ɨɬɧɨɲɟɧɢɹ ɦɟɠɞɭ ɞɜɭɦɹ ɝɪɭɩɩɚɦɢ ɱɢɫɬɨ ɤɨɧɤɭɪɟɧɬɧɵɟ. Ȼɵɥɨ ɩɨɤɚɡɚɧɨ, ɱɬɨ ɜ ɪɟɡɭɥɶɬɚɬɟ
ɜɨɡɦɭɳɟɧɢɹ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɨɞɧɨɪɨɞɧɚɹ ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ ɫɬɚɧɨɜɢɬɫɹ
ɝɟɬɟɪɨɝɟɧɧɨɣ.
Ɍɟɩɟɪɶ ɧɚɫ ɢɧɬɟɪɟɫɭɟɬ ɨɛɳɢɣ ɫɥɭɱɚɣ, ɤɨɝɞɚ ɧɚ ɫɢɫɬɟɦɭ (8.5.3) ɧɚɥɨɠɟɧɵ ɝɪɚɧɢɱɧɵɟ
ɭɫɥɨɜɢɹ ɇɟɣɦɚɧɚ, ɬ. ɟ. p
1
= ɪ
2
= 1 ɢ q
1
= q
2
= 0 ɢɥɢ
ɗɬɨ ɡɧɚɱɢɬ, ɱɬɨ ɦɢɝɪɚɰɢɹ ɦɟɠɞɭ ɝɨɪɨɞɨɦ ɢ «ɨɤɪɭɠɚɸɳɢɦ ɦɢɪɨɦ» ɨɬɫɭɬɫɬɜɭɟɬ. ȼɜɟɞɟɦ
ɜɟɥɢɱɢɧɵ
Ɍɟɨɪɟɦɚ 8.5.1. ɉɭɫɬɶ (X,Ȋ) — ɪɟɲɟɧɢɟ ɫɢɫɬɟɦɵ (8.5.3) ɫ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ (8.5.5), ɢ
ɩɭɫɬɶ ɜ ɤɚɠɞɨɣ ɬɨɱɤɟ r ∈ W ɧɚɱɚɥɶɧɵɟ ɭɫɥɨɜɢɹ ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɧɟɪɚɜɟɧɫɬɜɚɦ 0 < F(r) < ȝ ɢ 0
< H (r) <
δ
. Ɍɨɝɞɚ ɢɦɟɟɦ
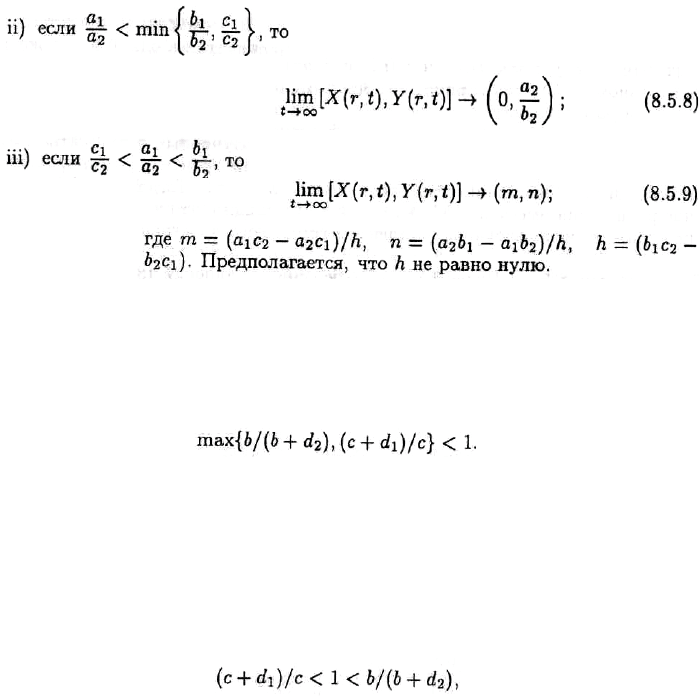
ɉɭɫɬɶ ɞɥɹ ɩɪɨɫɬɨɬɵ ɢɧɬɟɪɩɪɟɬɚɰɢɢ Θ
1
= Θ
2
= 0. ɇɟɪɚɜɟɧɫɬɜɨ 0 < F (r) ɨɡɧɚɱɚɟɬ, ɱɬɨ
ɧɚɱɚɥɶɧɚɹ ɩɥɨɬɧɨɫɬɶ ɧɚɫɟɥɟɧɢɹ ɝɪɭɩɩɵ 1 ɧɟ ɪɚɜɧɚ ɧɭɥɸ ɧɢ ɜ ɤɚɤɨɣ ɬɨɱɤɟ ɝɨɪɨɞɫɤɨɝɨ
ɩɪɨɫɬɪɚɧɫɬɜɚ. ȿɫɥɢ ɡɚɦɟɬɢɦ, ɱɬɨ
α
1
/c
1
= α/(ɫ + d
1
), ɬɨ ɩɪɚɜɚɹ ɱɚɫɬɶ ɧɟɪɚɜɟɧɫɬɜɚ F(r) < α/(ɫ +
d
1
) ɨɡɧɚɱɚɟɬ, ɱɬɨ ɧɚɱɚɥɶɧɚɹ ɩɥɨɬɧɨɫɬɶ ɝɪɭɩɩɵ 1 ɨɝɪɚɧɢɱɟɧɚ ɫɜɟɪɯɭ ɜɦɟɫɬɢɦɨɫɬɶɸ ɝɨɪɨɞɫɤɨɝɨ
ɩɪɨɫɬɪɚɧɫɬɜɚ ɢ ɨɛɴɟɦɨɦ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɡɚɧɹɬɨɝɨ ɝɪɭɩɩɨɣ 2. Ɍɚɤ ɤɚɤ α
2
/c
2
= α/(ɫ+ d
2
), ɦɵ
ɦɨɠɟɦ ɬɚɤ ɠɟ ɩɪɨɫɬɨ ɨɛɴɹɫɧɢɬɶ ɫɦɵɫɥ ɧɟɪɚɜɟɧɫɬɜɚ F(r) < α
2
/c
2
.
ɍɬɜɟɪɠɞɟɧɢɟ ɬɟɨɪɟɦɵ (i) ɜɵɩɨɥɧɹɟɬɫɹ, ɟɫɥɢ
ɉɨɫɥɟɞɧɟɟ ɫɩɪɚɜɟɞɥɢɜɨ ɜ ɬɨɦ ɫɥɭɱɚɟ, ɟɫɥɢ d
2
> 0 ɢ d
1
< 0. ɉɨɫɤɨɥɶɤɭ d
1
(d
2
) ɹɜɥɹɟɬɫɹ ɦɟɪɨɣ
ɜɨɡɞɟɣɫɬɜɢɹ ɝɪɭɩɩɵ 2 (ɝɪɭɩɩɵ 1) ɧɚ ɝɪɭɩɩɭ 1 (ɝɪɭɩɩɭ 2), ɦɵ ɜɢɞɢɦ, ɱɬɨ ɟɫɥɢ ɝɪɭɩɩɚ 1
ɫɬɪɟɦɢɬɫɹ ɠɢɬɶ ɜɛɥɢɡɢ ɝɪɭɩɩɵ 2, ɯɨɬɹ ɝɪɭɩɩɚ 2 ɧɚɫɬɪɨɟɧɚ ɧɟɞɪɭɠɟɥɸɛɧɨ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ
ɝɪɭɩɩɟ 1, ɬɨ ɝɪɭɩɩɚ 2 ɜ ɤɨɧɰɟ ɤɨɧɰɨɜ ɨɤɚɠɟɬɫɹ ɜɵɬɟɫɧɟɧɧɨɣ ɝɪɭɩɩɨɣ 1. Ɇɵ ɜɢɞɢɦ, ɤɚɤ
ɩɪɨɬɟɤɚɟɬ ɷɬɨɬ ɷɜɨɥɸɰɢɨɧɧɵɣ ɩɪɨɰɟɫɫ. Ⱥɫɢɦɩɬɨɬɢɱɟɫɤɨɟ ɪɚɜɧɨɜɟɫɢɟ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɜɟɥɢɱɢɧ
d
1
ɢ d
2
— ɷɬɨ ɟɫɬɟɫɬɜɟɧɧɨ, ɩɨɬɨɦɭ ɱɬɨ ɜ ɚɫɢɦɩɬɨɬɢɤɟ ɧɟɬ ɛɨɪɶɛɵ ɜ ɤɥɚɫɫɢɱɟɫɤɨɦ ɫɦɵɫɥɟ. Ɍɚɤ
ɤɚɤ ɏ(r, ∞) = ɚ/b, ɦɵ ɜɢɞɢɦ, ɱɬɨ ɜ ɩɪɟɞɟɥɟ ɜɫɹ ɝɨɪɨɞɫɤɚɹ ɟɦɤɨɫɬɶ ɛɭɞɟɬ ɢɫɩɨɥɶɡɨɜɚɧɚ ɝɪɭɩɩɨɣ
1: ɜ ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ ɝɪɭɩɩɚ 2 ɫɦɨɠɟɬ ɪɚɫɩɨɥɚɝɚɬɶ ɫɜɨɢ ɠɢɥɢɳɚ ɜ ɝɨɪɨɞɫɤɨɦ ɩɪɨɫɬɪɚɧɫɬɜɟ.
ɋɥɭɱɚɣ (ii) ɦɨɠɟɬ ɛɵɬɶ ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɧ ɚɧɚɥɨɝɢɱɧɵɦ ɨɛɪɚɡɨɦ.
ɉɨɫɤɨɥɶɤɭ ɭɫɥɨɜɢɟ (in) ɦɨɠɧɨ ɩɟɪɟɩɢɫɚɬɶ ɜ
ɮɨɪɦɟ
ɧɟɨɛɯɨɞɢɦɨ ɩɨɬɪɟɛɨɜɚɬɶ, ɱɬɨɛɵ d
1
ɢ d
2
ɛɵɥɢ ɨɬɪɢɰɚɬɟɥɶɧɵ — ɦɟɠɞɭ ɥɸɞɶɦɢ ɨɬɫɭɬɫɬɜɭɟɬ
ɚɧɬɢɩɚɬɢɹ (ɬɪɟɛɨɜɚɧɢɟ, ɤɨɬɨɪɨɟ ɞɨɜɨɥɶɧɨ
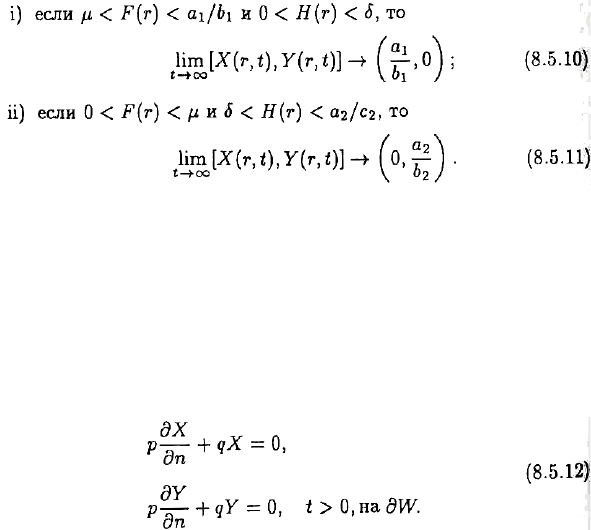
ɪɟɞɤɨ ɜɵɩɨɥɧɹɟɬɫɹ ɧɚ ɩɪɚɤɬɢɤɟ). ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɩɪɟɞɫɬɚɜɢɬɟɥɢ ɪɚɡɧɵɯ ɝɪɭɩɩ ɧɚɫɟɥɟɧɢɹ ɦɨɝɭɬ
ɩɪɨɠɢɜɚɬɶ ɧɚ ɨɞɧɨɣ ɢ ɬɨɣ ɠɟ ɬɟɪɪɢɬɨɪɢɢ. ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ (iii) ɜɵɩɨɥɧɹɟɬɫɹ ɬɨɥɶɤɨ ɩɪɢ
ɩɨɥɨɠɢɬɟɥɶɧɨɦ h. ɋɥɭɱɚɣ ɨɬɪɢɰɚɬɟɥɶɧɨɝɨ h ɦɵ ɨɛɫɭɞɢɦ ɧɢɠɟ.
ȿɫɥɢ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɩɟɪɟɤɪɟɫɬɧɵɟ ɱɥɟɧɵ d
1
XY ɢ d
2
XY ɤɚɤ ɨɬɪɚɠɟɧɢɟ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ
ɝɪɭɩɩ ɧɚ ɷɮɮɟɤɬɢɜɧɨɫɬɶ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɟɦɤɨɫɬɢ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɩɨɥɭɱɟɧɧɵɟ
ɪɟɡɭɥɶɬɚɬɵ ɫɬɚɧɨɜɹɬɫɹ ɢɧɬɭɢɬɢɜɧɨ ɩɪɢɟɦɥɟɦɵɦɢ. ȿɫɥɢ d
1
ɩɨɥɨɠɢɬɟɥɶɧɨ, ɬɨ ɧɟɤɨɬɨɪɚɹ ɱɚɫɬɶ
ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɧɟ ɦɨɠɟɬ ɛɵɬɶ ɷɮɮɟɤɬɢɜɧɨ ɢɫɩɨɥɶɡɨɜɚɧɚ. ɗɬɨ ɦɨɠɧɨ ɨɫɦɵɫɥɢɬɶ,
ɩɨɥɨɠɢɜ Θ
1
= 0. Ɍɨɝɞɚ ɜ ɫɥɭɱɚɟ ɪɚɜɧɨɜɟɫɢɹ ɢɦɟɟɦ Į = bɏ + ɫY + d
1
Y. Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɱɥɟɧ d
1
Y
ɧɟ ɨɬɪɚɠɚɟɬ ɢɫɩɨɥɶɡɨɜɚɧɢɟ ɧɚɫɟɥɟɧɢɟɦ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ.
Ɍɟɨɪɟɦɚ 8.5.2. ɉɭɫɬɶ (X,Ȋ) — ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɣ (8.5.3) ɫ ɭɱɟɬɨɦ ɝɪɚɧɢɱɧɵɯ ɭɫɥɨɜɢɣ
(8.5.5) ɢ b
1
/b
2
< Į
1
/Į
2
< c
1
/c
2
. Ɍɨɝɞɚ ɢɦɟɟɦ
ɉɨɫɤɨɥɶɤɭ ɭɫɥɨɜɢɹ b
1
/b
2
< Į
1
/Į
2
< c
1
/c
2
ɢɞɟɧɬɢɱɧɵ ɭɫɥɨɜɢɹɦ b/(b+ d
2
) < 1 < (ɫ+ d
1
)/c ɢ h <
0, ɧɟɨɛɯɨɞɢɦɨ, ɱɬɨɛɵ d
1
> 0 ɢ d
2
> 0. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɝɪɭɩɩɵ 1 ɢ 2 ɱɢɫɬɨ ɤɨɧɤɭɪɟɧɬɧɵ. ȼ ɷɬɨɦ
ɫɥɭɱɚɟ, ɩɨ ɩɪɨɲɟɫɬɜɢɢ ɜɪɟɦɟɧɢ, ɜɵɠɢɜɟɬ ɬɨɥɶɤɨ ɨɞɧɚ ɝɪɭɩɩɚ. Ɇɨɠɧɨ ɩɪɨɜɟɪɢɬɶ, ɱɬɨ ɫɢɫɬɟɦɚ
ɢɦɟɟɬ ɞɜɚ ɭɫɬɨɣɱɢɜɵɯ ɢ ɞɜɚ ɧɟɭɫɬɨɣɱɢɜɵɯ ɩɨɫɬɨɹɧɧɵɯ ɫɬɚɰɢɨɧɚɪɧɵɯ ɪɟɲɟɧɢɹ.
Ⱥɫɢɦɩɬɨɬɢɱɟɫɤɨɟ ɪɚɜɧɨɜɟɫɢɟ ɡɚɜɢɫɢɬ ɨɬ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ. ȼ ɫɥɭɱɚɟ (i), ɬɚɤ ɤɚɤ ɩɥɨɬɧɨɫɬɶ
ɧɚɫɟɥɟɧɢɹ ɝɪɭɩɩɵ 1 ɨɱɟɧɶ ɜɵɫɨɤɚ, ɚ ɝɪɭɩɩɵ 2 ɧɢɡɤɚ, ɝɪɭɩɩɚ 2 ɞɨɥɠɧɚ ɛɵɬɶ
ɜɵɬɟɫɧɟɧɚ ɜ ɤɨɧɰɟ
ɤɨɧɰɨɜ ɝɪɭɩɩɨɣ 1. Ⱥɧɚɥɨɝɢɱɧɨ ɦɨɠɧɨ ɨɛɴɹɫɧɢɬɶ ɫɥɭɱɚɣ (ii). Ɂɞɟɫɶ ɭɦɟɫɬɧɨ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɩɨɞ
ɜɵɬɟɫɧɟɧɢɟɦ ɦɵ ɩɨɧɢɦɚɟɦ ɢɫɱɟɡɧɨɜɟɧɢɟ ɜ ɛɢɨɥɨɝɢɱɟɫɤɨɦ ɫɦɵɫɥɟ, ɩɨɬɨɦɭ ɱɬɨ ɦɢɝɪɚɰɢɹ ɜ
ɦɨɞɟɥɢ ɧɟ ɩɪɟɞɭɫɦɚɬɪɢɜɚɟɬɫɹ.
ȼɵɲɟ ɦɵ «ɢɡɨɥɢɪɨɜɚɥɢ» ɝɨɪɨɞɫɤɭɸ ɫɢɫɬɟɦɭ, ɡɚɞɚɜ ɧɚ ɝɪɚɧɢɰɟ ɭɫɥɨɜɢɹ ɇɟɣɦɚɧɚ.
ɂɧɬɟɪɟɫɧɨ ɩɨɫɦɨɬɪɟɬɶ, ɱɬɨ ɩɪɨɢɡɨɣɞɟɬ, ɟɫɥɢ ɦɵ «ɨɬɤɪɨɟɦ» ɫɢɫɬɟɦɭ. Ɋɚɫɫɦɨɬɪɢɦ ɫɥɟɞɭɸɳɟɟ
ɝɪɚɧɢɱɧɨɟ ɭɫɥɨɜɢɟ:
