Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории

Подождите немного. Документ загружается.

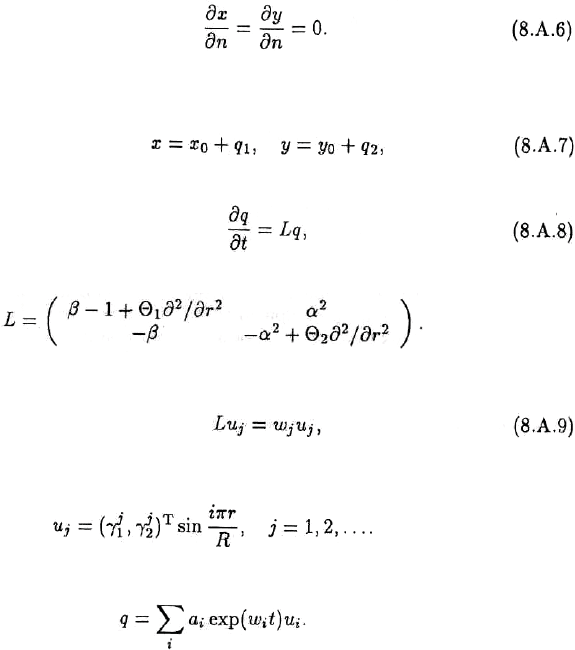
ɢɥɢ

Ɇɵ ɪɚɫɫɦɨɬɪɢɦ ɡɞɟɫɶ ɬɨɥɶɤɨ ɭɫɥɨɜɢɹ Ⱦɢɪɢɯɥɟ. Ⱥɧɚɥɨɝɢɱɧɵɣ ɚɧɚɥɢɡ ɞɥɹ ɭɫɥɨɜɢɣ ɧɭɥɟɜɨɝɨ

ɩɨɬɨɤɚ ɱɟɪɟɡ ɝɪɚɧɢɰɭ ɩɪɢɜɟɞɟɧ ɜ ɤɧɢɝɟ ɇɢɤɨɥɢɫɚ ɢ ɉɪɢɝɨɠɢɧɚ (1977).

ȿɞɢɧɫɬɜɟɧɧɵɦ ɨɞɧɨɪɨɞɧɵɦ ɫɬɚɰɢɨɧɚɪɧɵɦ ɪɟɲɟɧɢɟɦ ɡɚɞɚɱɢ ɹɜɥɹɟɬɫɹ ɪɟɲɟɧɢɟ x

= α, ɭ

ȕ/α. ȼɜɟɞɹ ɦɚɥɵɟ ɜɨɡɦɭɳɟɧɢɹ q = (q

, q

)

ɤɚɤ

ɧɚɯɨɞɢɦ ɫɥɟɞɭɸɳɢɣ ɜɢɞ ɥɢɧɟɚɪɢɡɨɜɚɧɧɵɯ ɭɪɚɜɧɟɧɢɣ:

ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɯ ɧɚ ɝɪɚɧɢɰɟ ɭɫɥɨɜɢɹɦ q

= q

= 0. Ʌɢɧɟɚɪɢɡɨɜɚɧɧɵɣ ɨɩɟɪɚɬɨɪ ɢɦɟɟɬ ɜɢɞ

Ⱦɥɹ ɚɧɚɥɢɡɚ ɚɫɢɦɩɬɨɬɢɱɟɫɤɨɝɨ ɩɨɜɟɞɟɧɢɹ ɪɟɲɟɧɢɣ ɫɢɫɬɟɦɵ (8.Ⱥ.8) ɞɨɫɬɚɬɨɱɧɨ ɧɚɣɬɢ

ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ w

ɢ ɫɨɛɫɬɜɟɧɧɵɟ ɜɟɤɬɨɪɵ u

[=(u

, u

)

] ɥɢɧɟɣɧɨɝɨ ɨɩɟɪɚɬɨɪɚ L

ɫ ɭɱɟɬɨɦ ɭɫɥɨɜɢɣ ɧɚ ɝɪɚɧɢɰɟ u

= 0 (j = 0,1,...). Ɋɟɲɟɧɢɹɦɢ ɭɪɚɜɧɟɧɢɣ (8.Ⱥ.9) ɹɜɥɹɸɬɫɹ

ɮɭɧɤɰɢɢ

ȼɟɤɬɨɪ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ q ɦɨɠɧɨ ɜɵɪɚɡɢɬɶ ɤɚɤ

ɍɩɨɦɹɧɭɬɨɟ ɫɬɚɰɢɨɧɚɪɧɨɟ ɫɨɫɬɨɹɧɢɟ (

, ȕ/Į) ɚɫɢɦɩɬɨɬɢɱɟɫɤɢ ɭɫɬɨɣɱɢɜɨ, ɟɫɥɢ ɞɥɹ ɜɫɟɯ i

ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ w

, ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɧɟɪɚɜɟɧɫɬɜɭ Re(w

) < 0. ȿɫɥɢ ɞɥɹ ɧɟɤɨɬɨɪɨɝɨ i ɢɦɟɟɬ

ɦɟɫɬɨ Re (w

) > 0, ɬɨ ɪɟɲɟɧɢɟ ɧɟɭɫɬɨɣɱɢɜɨ. ȼ ɫɥɭɱɚɟ Re(w

) = 0 ɩɪɢ ɭɫɥɨɜɢɢ ɫɨɛɫɬɜɟɧɧɨɝɨ

ɡɧɚɱɟɧɢɹ ɧɟɱɟɬɧɨɣ ɤɪɚɬɧɨɫɬɢ ɢɦɟɟɬ ɦɟɫɬɨ

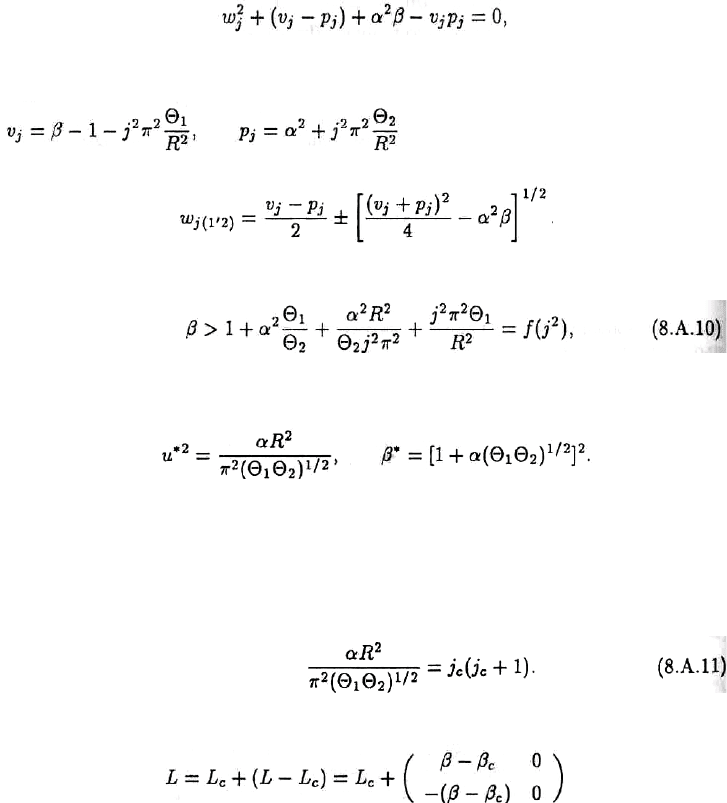
ɹɜɥɟɧɢɟ ɛɢɮɭɪɤɚɰɢɢ. ɇɟɬɪɭɞɧɨ ɩɨɥɭɱɢɬɶ ɫɥɟɞɭɸɳɟɟ ɯɚɪɚɤɬɟɪɢɫɬɢɱɟɫɤɨɟ ɭɪɚɜɧɟɧɢɟ ɡɚɞɚɱɢ:

Ɋɟɲɟɧɢɟ ɯɚɪɚɤɬɟɪɢɫɬɢɱɟɫɤɨɝɨ ɭɪɚɜɧɟɧɢɹ ɞɚɟɬ

Ɉɬɫɸɞɚ ɥɟɝɤɨ ɩɨɥɭɱɢɬɶ ɭɫɥɨɜɢɹ ɭɫɬɨɣɱɢɜɨɫɬɢ. ɇɚɫ ɢɧɬɟɪɟɫɭɟɬ ɩɨɜɟɞɟɧɢɟ ɫɢɫɬɟɦɵ ɜ

ɭɫɥɨɜɢɹɯ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ. Ɉɛɫɭɞɢɦ ɫɥɭɱɚɣ ɞɟɣɫɬɜɢɬɟɥɶɧɨɝɨ w

. ɉɪɢ v

— Į

ȕ > 0 ɢɥɢ

ɯɚɪɚɤɬɟɪɢɫɬɢɱɟɫɤɨɟ ɭɪɚɜɧɟɧɢɟ ɢɦɟɟɬ ɨɞɢɧ ɩɨɥɨɠɢɬɟɥɶɧɵɣ ɤɨɪɟɧɶ. ɇɚ ɪɢɫ. 8.15 ɩɪɢɜɟɞɟɧɚ

ɤɪɢɜɚɹ ȕ ɤɚɤ ɮɭɧɤɰɢɹ ɨɬ j. ɋ ɪɨɫɬɨɦ ȕ ɩɟɪɜɵɣ ɭɱɚɫɬɨɤ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ ɜɨɡɧɢɤɚɟɬ ɩɪɢ ȕ = ȕ

ɫɨɨɬɜɟɬɫɬɜɭɹ ɰɟɥɨɦɭ j

, ɛɥɢɠɚɣɲɟɦɭ ɤ ɦɢɧɢɦɭɦɭ (ɢ

, ȕ

), ɝɞɟ

ɂɡ ɪɢɫɭɧɤɚ ɜɢɞɧɨ, ɱɬɨ ɩɟɪɜɚɹ ɬɨɱɤɚ ɛɢɮɭɪɤɚɰɢɢ ȕ

ɥɟɠɢɬ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɦɢɧɢɦɭɦɚ ȕ

ɝɪɚɧɢɱɧɨɣ ɤɪɢɜɨɣ ɭɫɬɨɣɱɢɜɨɫɬɢ (ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ȕ

ɧɟ ɪɚɜɧɨ ȕ

Ɉɩɪɟɞɟɥɢɦ ɭɫɥɨɜɢɹ, ɩɪɢ ɤɨɬɨɪɵɯ ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ w

ɢɦɟɟɬ ɞɜɨɣɧɨɟ ɜɵɪɨɠɞɟɧɢɟ.

ɉɨɫɤɨɥɶɤɭ ȕ ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɟɣ j

, ɜɫɟ, ɱɬɨ ɧɚɦ ɧɭɠɧɨ — ɷɬɨ ɡɚɩɢɫɚɬɶ ɭɪɚɜɧɟɧɢɟ ɜ ɜɢɞɟ (j

j )(j

—

j ) = 0, ɝɞɟ j

ɢ j

— ɞɜɚ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɰɟɥɵɯ ɱɢɫɥɚ. ȼ ɱɚɫɬɧɨɫɬɢ, ɟɫɥɢ ɦɵ

ɩɪɢɦɟɦ j

= j

≤

, ɬɨ ɫ ɧɟɨɛɯɨɞɢɦɨɫɬɶɸ ɩɨɥɭɱɢɦ j

= j

+ 1. Ɇɨɠɧɨ ɭɫɬɚɧɨɜɢɬɶ, ɱɬɨ ɷɬɨ

ɭɫɥɨɜɢɟ ɭɞɨɜɥɟɬɜɨɪɹɟɬɫɹ, ɟɫɥɢ

ɑɬɨɛɵ ɡɚɩɢɫɚɬɶ ɹɜɧɵɣ ɜɢɞ ɪɟɲɟɧɢɣ, ɛɢɮɭɪɰɢɪɭɸɳɢɯ ɨɬ ɤɪɢɬɢɱɟɫɤɨɣ ɬɨɱɤɢ ȕ

, ɪɚɡɥɨɠɢɦ

ɨɩɟɪɚɬɨɪ L ɜ ɫɭɦɦɭ

ɝɞɟ

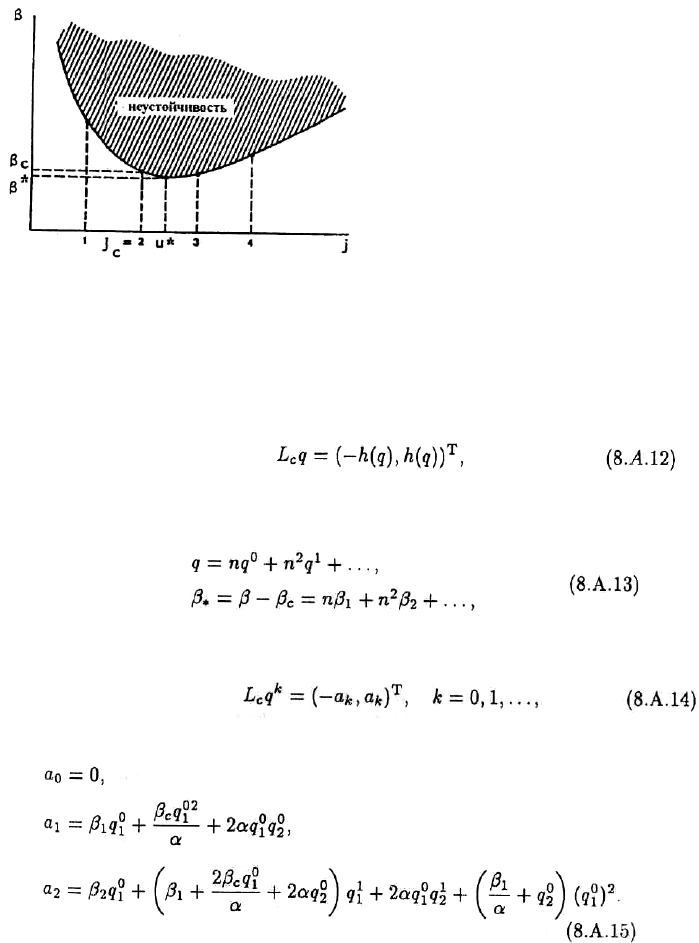
Ɋɢɫ. 8.15. Ⱦɢɚɝɪɚɦɦɚ ɥɢɧɟɣɧɨɣ ɭɫɬɨɣɱɢɜɨɫɬɢ ɫ ɛɢɮɭɪɤɚɰɢɟɣ ɫɬɚɰɢɨɧɚɪɧɵɯ ɪɟɲɟɧɢɣ.

ɝɞɟ L

— ɨɩɟɪɚɬɨɪ, ɜɵɱɢɫɥɟɧɧɵɣ ɜ ɤɪɢɬɢɱɟɫɤɨɣ ɬɨɱɤɟ ɩɟɪɜɨɣ ɛɢɮɭɪɤɚɰɢɢ. Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ,

ɱɬɨ L

ɹɜɥɹɟɬɫɹ ɩɚɪɚɛɨɥɢɱɟɫɤɢɦ ɨɩɟɪɚɬɨɪɨɦ, ɤɨɬɨɪɵɣ ɞɨɩɭɫɤɚɟɬ ɟɞɢɧɫɬɜɟɧɧɵɣ ɧɭɥɟɜɨɣ

ɫɨɛɫɬɜɟɧɧɵɣ ɜɟɤɬɨɪ u

(ı = j

), ɢɥɢ ɠɟ ɢɦɟɟɬ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɫ ɨɬɪɢɰɚɬɟɥɶɧɵɦɢ

ɞɟɣɫɬɜɢɬɟɥɶɧɵɦɢ ɱɚɫɬɹɦɢ.

ɉɨɞɫɬɚɜɥɹɹ ∂ɢ/

∂

t = 0, ɦɵ ɦɨɠɟɦ ɡɚɩɢɫɚɬɶ (8.Ⱥ.4) ɜ ɜɢɞɟ

ɝɞɟ h(q) = (ȕ-ȕ

αα

+ȕ

q /α

αα

α+

q q

. ɑɬɨɛɵ ɧɚɣɬɢ ɪɟɲɟɧɢɟ,

ɩɨɥɨɠɢɦ

ɝɞɟ n — ɦɚɥɵɣ ɩɚɪɚɦɟɬɪ ɪɚɡɥɨɠɟɧɢɹ, ɢ q

= (

q ,

q )

. ɉɨɞɫɬɚɜɥɹɹ (8.Ⱥ.13) ɜ (8.Ⱥ.12) ɢ

ɩɪɢɪɚɜɧɢɜɚɹ ɡɚɬɟɦ ɨɞɢɧɚɤɨɜɵɟ ɫɬɟɩɟɧɢ n, ɩɨɥɭɱɢɦ ɭɪɚɜɧɟɧɢɟ

ɭɞɨɜɥɟɬɜɨɪɹɸɳɟɟ ɭɫɥɨɜɢɸ q

= 0 (k = 0,1,...) ɧɚ ɝɪɚɧɢɰɟ. ɉɟɪɜɵɟ

ɧɟɫɤɨɥɶɤɨ ɤɨɷɮɮɢɰɢɟɧɬɨɜ a

ɢɦɟɸɬ ɜɢɞ

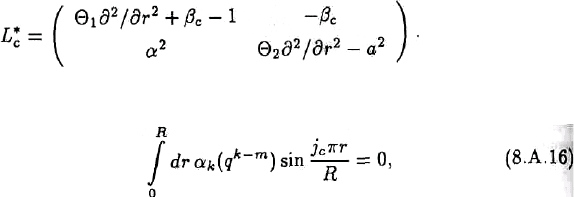
ɋɨɝɥɚɫɧɨ ɚɥɶɬɟɪɧɚɬɢɜɟ Ɏɪɟɞɝɨɥɶɦɚ (ɫɦ. Ƀɨɫɫ ɢ Ⱦɠɨɡɟɮ, 1980), ɧɚɦ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɜɟɤɬɨɪ q

ɹɜɥɹɟɬɫɹ ɪɟɲɟɧɢɟɦ ɭɪɚɜɧɟɧɢɹ (8.Ⱥ.14) ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɩɪɚɜɚɹ ɱɚɫɬɶ (8.Ⱥ.14) ɨɪɬɨɝɨɧɚɥɶɧɚ

ɧɭɥɟɜɨɦɭ ɫɨɛɫɬɜɟɧɧɨɦɭ ɜɟɤɬɨɪɭ ɫɨɩɪɹɠɟɧɧɨɝɨ ɨɩɟɪɚɬɨɪɚ

L , ɝɞɟ

ɍɪɚɜɧɟɧɢɟ (8.Ⱥ.14) ɦɵ ɦɨɠɟɦ ɪɟɲɢɬɶ. Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ (ɇɢɤɨɥɢɫ ɢ ɉɪɢɝɨɠɢɣ, 1977), ɱɬɨ

ɚɥɶɬɟɪɧɚɬɢɜɚ Ɏɪɟɞɝɨɥɶɦɚ ɢɦɟɟɬ ɦɟɫɬɨ, ɟɫɥɢ ɜ ɧɚɲɟɣ ɡɚɞɚɱɟ

ɝɞɟ 0 < m ≤; k = 1,... ɂɡ (8.Ⱥ.16) ɜɢɞɢɦ, ɱɬɨ ɪɟɲɟɧɢɟ ɡɚɜɢɫɢɬ ɨɬ ɬɨɝɨ, ɱɟɬɧɨ ɢɥɢ ɧɟɱɟɬɧɨ ɱɢɫɥɨ

ɍɫɥɨɜɢɹ (8.Ⱥ.16) ɜɦɟɫɬɟ ɫ (8.Ⱥ.15) ɩɨɡɜɨɥɹɸɬ ɨɩɪɟɞɟɥɢɬɶ ɤɨɷɮɮɢɰɢɟɧɬɵ ȕ

. ɂɡ ɜɬɨɪɨɝɨ

ɫɨɨɬɧɨɲɟɧɢɹ ɜ (8.Ⱥ.13) ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɚɪɚɦɟɬɪ n ɤɚɤ ɮɭɧɤɰɢɹ ɪɚɡɧɨɫɬɢ b - b

. Ɍɚɤɢɦ

ɨɛɪɚɡɨɦ, ɦɵ ɦɨɠɟɦ ɧɚɣɬɢ q ɤɚɤ ɮɭɧɤɰɢɸ ȕ – ȕ

. Ⱦɚɥɟɟ ɦɵ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɩɟɪɜɵɟ

ɧɟɫɤɨɥɶɤɨ ɱɥɟɧɨɜ ȕ

ɦɵ ɪɚɫɫɱɢɬɚɥɢ.

ɋ ɭɱɟɬɨɦ ɷɬɢɯ ɪɟɡɭɥɶɬɚɬɨɜ ɦɨɠɟɬ ɛɵɬɶ ɞɨɤɚɡɚɧɚ ɫɥɟɞɭɸɳɚɹ ɬɟɨɪɟɦɚ (ɫɦ. ɇɢɤɨɥɢɫ ɢ

ɉɪɢɝɨɠɢɣ, 1977).

Ɍɟɨɪɟɦɚ 8.A.1.

i) ɉɭɫɬɶ j

ɱɟɬɧɨ. ȼ ɨɤɪɟɫɬɧɨɫɬɢ ɨɫɨɛɨɣ ɬɨɱɤɢ ȕ

ɧɨɜɵɟ ɛɢɮɭɪɤɚɰɢɨɧɧɵɟ ɪɟɲɟɧɢɹ ɛɭɞɭɬ

ɚɫɢɦɩɬɨɬɢɱɟɫɤɢ ɭɫɬɨɣɱɢɜɵ ɜ ɫɭɩɟɪɤɪɢɬɢɱɟɫɤɨɣ ɨɛɥɚɫɬɢ ȕ > ȕ

(ȕ

> 0). Ɉɞɧɚɤɨ ɩɪɢ ȕ

< 0 ɫɭɛɤɪɢɬɢɱɟɫɤɢɟ ɜɟɬɜɢ ɧɟɭɫɬɨɣɱɢɜɵ.

ii) ɉɭɫɬɶ j

ɧɟɱɟɬɧɨ. Ɍɨɝɞɚ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ȕ

ɛɢɮɭɪɤɚɰɢɨɧɧɨɟ ɪɟɲɟɧɢɟ ɨɩɪɟɞɟɥɟɧɨ ɞɥɹ ȕ

ɩɨ ɨɛɟ ɫɬɨɪɨɧɵ ɨɬ ȕ

. ɇɨɜɨɟ ɛɢɮɭɪɤɚɰɢɨɧɧɨɟ ɪɟɲɟɧɢɟ ɭɫɬɨɣɱɢɜɨ ɧɚ

ɫɭɩɟɪɤɪɢɬɢɱɟɫɤɨɣ ɜɟɬɜɢ, ɤɨɝɞɚ ȕ > ȕ

, ɢ ɧɟɭɫɬɨɣɱɢɜɨ ɧɚ ɫɭɛɤɪɢɬɢɱɟɫɤɨɣ ɜɟɬɜɢ, ɤɨɝɞɚ

ȕ < ȕ

ɇɚ ɪɢɫ. 8.16 ɞɚɧɚ ɢɥɥɸɫɬɪɚɰɢɹ ɫɥɭɱɚɹ (i) ɬɟɨɪɟɦɵ, ɚ ɧɚ ɪɢɫ. 8.17 — ɫɥɭɱɚɹ (ii).

ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɧɚɢɛɨɥɟɟ ɜɚɠɧɵɦ ɫɜɨɣɫɬɜɨɦ ɞɢɫɫɢɩɚɬɢɜ-ɧɵɯ ɫɬɪɭɤɬɭɪ,

ɩɨɥɭɱɟɧɧɵɯ ɩɪɢ ɨɩɢɫɚɧɧɵɯ ɜɵɲɟ ɛɢɮɭɪɤɚɰɢɹɯ, ɹɜɥɹɟɬɫɹ ɢɯ ɚɫɢɦɦɟɬɪɢɱɧɵɣ ɯɚɪɚɤɬɟɪ. Ʉɨɝɞɚ

ɨɩɪɟɞɟɥɟɧɧɨɟ ɤɪɢɬɢɱɟɫɤɨɟ ɡɧɚɱɟɧɢɟ

ɩɚɪɚɦɟɬɪɚ ȕ ɩɪɟɜɵɲɟɧɨ, ɫɚɦɨɟ ɫɢɦɦɟɬɪɢɱɧɨɟ ɢɡ

ɪɟɲɟɧɢɣ ɩɟɪɟɫɬɚɟɬ ɛɵɬɶ ɭɫɬɨɣɱɢɜɵɦ, ɢ ɫɢɫɬɟɦɚ ɩɟɪɟɯɨɞɢɬ ɤ ɪɟɲɟɧɢɸ ɫ ɦɟɧɶɲɟɣ

ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɣ ɫɢɦɦɟɬɪɢɟɣ. ȼ ɩɪɟɞɵɞɭɳɟɦ

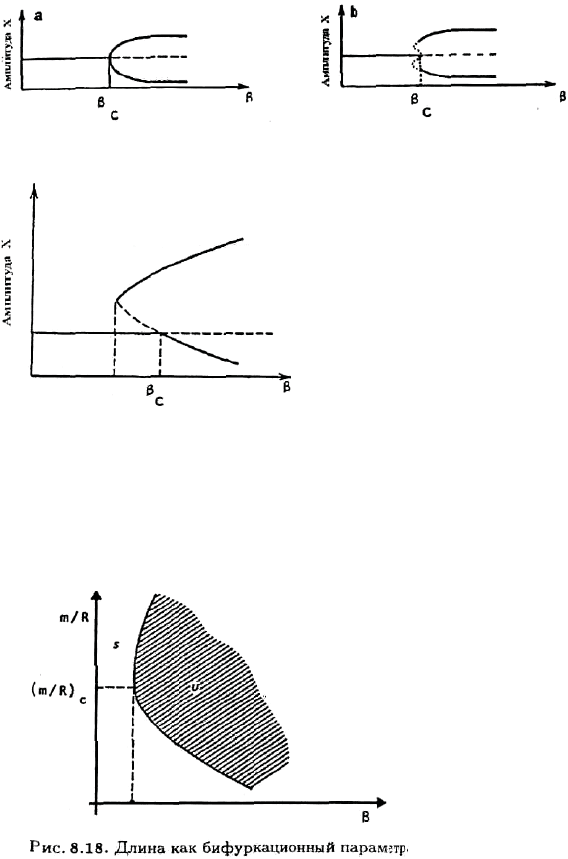
Ɋɢɫ. 8.16. Ȼɢɮɭɪɤɚɰɢɨɧɧɚɹ ɞɢɚɝɪɚɦɦɚ ɞɥɹ ɱɟɬɧɨɝɨ

: ɚ) ɫɭɩɟɪɤɪɢɬɢɱɟɫɤɚɹ ɜɟɬɜɶ, b)

ɫɭɛɤɪɢɬɢɱɟɫɤɚɹ ɜɟɬɜɶ.

Ɋɢɫ. 8.17. Ȼɢɮɭɪɤɚɰɢɨɧɧɚɹ ɞɢɚɝɪɚɦɦɚ ɞɥɹ ɧɟɱɟɬɧɨɝɨ j

ɩɪɢɦɟɪɟ, ɤɨɝɞɚ j

ɱɟɬɧɨ, ɫɢɫɬɟɦɚ ɢɦɟɟɬ ɚɩɪɢɨɪɧɨ ɪɚɜɧɵɟ ɜɟɪɨɹɬɧɨɫɬɢ ɪɚɡɜɢɜɚɬɶɫɹ ɜ ɫɬɨɪɨɧɭ

ɨɛɨɢɯ ɪɟɲɟɧɢɣ ɩɨ ɬɭ ɫɬɨɪɨɧɭ ɩɟɪɟɯɨɞɚ, ɤɨɬɨɪɵɣ ɡɚɜɢɫɢɬ ɨɬ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ.

Ⱦɪɭɝɢɦ ɢɧɬɟɪɟɫɧɵɦ ɚɫɩɟɤɬɨɦ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ ɚɧɚɥɢɡɚ ɹɜɥɹɟɬɫɹ ɬɪɚɤɬɨɜɤɚ ɪɚɡɦɟɪɚ

ɫɢɫɬɟɦɵ R ɤɚɤ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ ɩɚɪɚɦɟɬɪɚ. ɂɧɬɟɪɟɫɧɨ ɪɚɫɫɦɨɬɪɟɬɶ ɜɥɢɹɧɢɟ ɯɚɪɚɤɬɟɪɧɨɣ

ɞɥɢɧɵ ɧɚ ɨɛɪɚɡɨɜɚɧɢɟ ɞɢɫɫɢɩɚɬɢɜɧɵɯ ɫɬɪɭɤɬɭɪ ɩɪɢ ɩɨɫɬɟɩɟɧɧɨɦ ɢɡɦɟɧɟɧɢɢ ɮɨɪɦɵ ɢɥɢ

ɪɚɡɦɟɪɨɜ ɫɢɫɬɟɦɵ. ɗɬɭ

ɡɚɞɚɱɭ ɦɨɠɧɨ ɚɧɚɥɢɡɢɪɨɜɚɬɶ ɬɚɤɢɦ ɠɟ

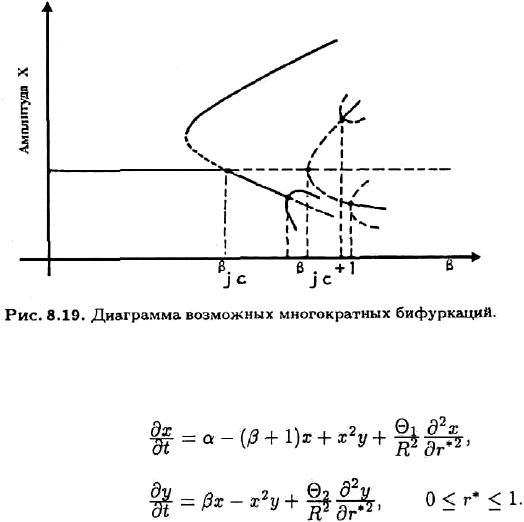
ɨɛɪɚɡɨɦ, ɤɚɤ ɢ ɩɪɟɞɵɞɭɳɭɸ. ȼɜɟɞɹ r

= r/R, ɦɵ ɩɨɥɭɱɢɦ ɧɨɜɵɣ ɜɢɞ ɭɪɚɜɧɟɧɢɣ (8. Ⱥ. 4)

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɡɦɟɧɟɧɢɟ R ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɢɡɦɟɧɟɧɢɟ ɞɢɮɮɭɡɢɨɧɧɵɯ

ɤɨɷɮɮɢɰɢɟɧɬɨɜ ɧɚɲɟɣ ɡɚɞɚɱɢ. Ɇɵ ɦɨɠɟɦ ɩɨɥɭɱɢɬɶ ɞɢɚɝɪɚɦɦɭ ɥɢɧɟɣɧɨɣ ɭɫɬɨɣɱɢɜɨɫɬɢ

ɫɬɚɰɢɨɧɚɪɧɨɝɨ ɪɟɲɟɧɢɹ (ɪɢɫ. 8.18), ɚɧɚɥɨɝɢɱɧɭɸ ɞɢɚɝɪɚɦɦɟ ɧɚ ɪɢɫ. 8.15, ɝɞɟ ɬ — ɩɪɨɢɡɜɨ-

ɥɶɧɨɟ ɰɟɥɨɟ ɱɢɫɥɨ, ɯɚɪɚɤɬɟɪɢɡɭɸɳɟɟ ɝɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ.

Ʉɚɤ ɩɨɤɚɡɚɥɢ ɇɢɤɨɥɢɫ ɢ ɉɪɢɝɨɠɢɣ (1977), ɜ ɷɬɨɣ ɦɨɞɟɥɢ ɬɚɤɠɟ ɧɚɛɥɸɞɚɸɬɫɹ

ɦɧɨɝɨɤɪɚɬɧɵɟ ɛɢɮɭɪɤɚɰɢɢ. ɇɚ ɪɢɫ. 8.19 ɩɪɟɞɫɬɚɜɥɟɧ ɬɢɩɢɱɧɵɣ

ɫɥɭɱɚɣ ɬɚɤɢɯ ɛɢɮɭɪɤɚɰɢɣ.

ɋɈȾȿɊɀȺɇɂȿ

9 ɉɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ ɢ ɦɚɫɲɬɚɛ ɜɪɟɦɟɧɢ ɜ ɷɤɨɧɨɦɢɱɟɫɤɨɦ ɚɧɚɥɢɡɟ 268

9.1 ɉɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ 268

9.2 Ɍɟɨɪɟɦɚ ɨ ɰɟɧɬɪɚɥɶɧɨɦ ɦɧɨɝɨɨɛɪɚɡɢɢ 272

9.3 ɋɢɧɝɭɥɹɪɧɵɟ ɜɨɡɦɭɳɟɧɢɹ 276

9.4 ɋɜɹɡɶ ɛɵɫɬɪɵɯ ɢ ɦɟɞɥɟɧɧɵɯ ɩɟɪɟɦɟɧɧɵɯ ɜ ɷɤɨɧɨɦɢɱɟɫɤɨɦ ɚɧɚɥɢɡɟ 280

9.5 Ɇɚɫɲɬɚɛ ɜɪɟɦɟɧɢ ɜ ɷɤɨɧɨɦɢɱɟɫɤɨɦ ɚɧɚɥɢɡɟ 284

9.6 Ⱦɢɧɚɦɢɤɚ ɱɟɥɨɜɟɤɚ. ɉɨɩɵɬɤɚ ɨɫɦɵɫɥɟɧɢɹ 289

ɉɪɢɥɨɠɟɧɢɟ: ɉɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɞɥɹ ɫɬɨɯɚɫɬɢɱɟɫɤɢɯ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɯ ɭɪɚɜɧɟɧɢɣ

291

10 ɋɢɧɟɪɝɟɬɢɱɟɫɤɚɹ ɷɤɨɧɨɦɢɤɚ ɢ ɟɟ ɡɧɚɱɟɧɢɟ 295

10.1 ɋɢɧɟɪɝɟɬɢɱɟɫɤɚɹ ɷɤɨɧɨɦɢɤɚ ɢ ɟɟ ɫɜɹɡɶ ɫ ɫɢɧɟɪɝɟɬɢɤɨɣ 296

10.2 ɋɜɹɡɶ ɫɢɧɟɪɝɟɬɢɱɟɫɤɨɣ ɷɤɨɧɨɦɢɤɢ ɫ ɬɪɚɞɢɰɢɨɧɧɨɣ ɬɟɨɪɢɟɣ ɷɤɨɧɨɦɢɱɟɫɤɨɣ

ɞɢɧɚɦɢɤɢ | 297

10.3 Ʉɨɧɤɭɪɟɧɬɧɚɹ ɢ ɩɥɚɧɨɜɚɹ ɷɤɨɧɨɦɢɤɚ ɫ ɬɨɱɤɢ ɡɪɟɧɢɹ ɫɢɧɟɪɝɟɬɢɱɟɫɤɨɣ

ɷɤɨɧɨɦɢɤɢ 303

10.4 Ɋɚɡɜɢɬɚɹ ɢ ɪɚɡɜɢɜɚɸɳɚɹɫɹ ɦɨɞɟɥɢ ɷɤɨɧɨɦɢɤɢ ɫ ɬɨɱɤɢ ɡɪɟɧɢɹ

ɫɢɧɟɪɝɟɬɢɱɟɫɤɨɣ ɷɤɨɧɨɦɢɤɢ 306

10.5 ɋɥɭɱɚɣɧɨɫɬɶ ɢ ɧɟɨɛɯɨɞɢɦɨɫɬɶ ɜ ɷɤɨɧɨɦɢɱɟɫɤɨɣ ɠɢɡɧɢ 310

10.6 Ɋɨɥɶ ɩɨɥɢɬɢɱɟɫɤɨɝɨ ɪɟɲɟɧɢɹ ɜ ɯɚɨɬɢɱɟɫɤɨɦ ɦɢɪɟ 311

10.7 ɋɨɨɬɧɨɲɟɧɢɟ ɦɟɠɞɭ ɦɢɤɪɨ- ɢ ɦɚɤɪɨɷɤɨɧɨɦɢɤɨɣ 313

11 ȼɵɜɨɞɵ ɢ ɩɟɪɫɩɟɤɬɢɜɵ ɞɚɥɶɧɟɣɲɢɯ ɢɫɫɥɟɞɨɜɚɧɢɣ 317

9 ɉɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ

ɢ ɦɚɫɲɬɚɛ ɜɪɟɦɟɧɢ ɜ

ɷɤɨɧɨɦɢɱɟɫɤɨɦ ɚɧɚɥɢɡɟ

... Ɏɚɤɬɢɱɟɫɤɢ ɦɵ ɫɬɚɜɢɦ ɜɨɩɪɨɫ ɨ ɩɨɧɢɦɚɧɢɢ, ɢ ɷɬɨ

ɜɫɟɝɞɚ ɨɤɚɡɵɜɚɟɬɫɹ ɡɚɞɚɱɟɣ ɨ ɡɚɞɚɱɟ, ɬ. ɟ., ɜɨɨɛɳɟ

ɝɨɜɨɪɹ, ɩɪɨɛɥɟɦɨɣ ɛɨɥɟɟ ɜɵɫɨɤɨɝɨ ɭɪɨɜɧɹ.

Ʉɚɪɥ Ɋ. ɉɨɩɩɟɪ

Ɉɫɧɨɜɧɚɹ ɰɟɥɶ ɞɚɧɧɨɣ ɤɧɢɝɢ — ɢɫɫɥɟɞɨɜɚɧɢɟ ɩɨɜɟɞɟɧɢɹ ɧɟɥɢɧɟɣɧɵɯ ɧɟɭɫɬɨɣɱɢɜɵɯ

ɞɢɧɚɦɢɱɟɫɤɢɯ ɷɤɨɧɨɦɢɱɟɫɤɢɯ ɫɢɫɬɟɦ. Ɉɫɨɛɟɧɧɨ ɢɧɬɟɪɟɫɭɟɬ ɧɚɫ ɩɨɜɟɞɟɧɢɟ ɫɢɫɬɟɦɵ

ɜɛɥɢɡɢ ɤɪɢɬɢɱɟɫɤɨɣ ɬɨɱɤɢ. ɇɚ ɩɪɟɞɵɞɭɳɢɯ ɩɪɢɦɟɪɚɯ ɦɵ ɩɨɤɚɡɚɥɢ, ɱɬɨ ɤɨɝɞɚ ɢɡ-ɡɚ

ɦɚɥɨɝɨ ɢɡɦɟɧɟɧɢɹ ɩɚɪɚɦɟɬɪɨɜ ɬɟɪɹɟɬɫɹ ɥɢɧɟɣɧɚɹ ɭɫɬɨɣɱɢɜɨɫɬɶ, ɜ ɯɚɪɚɤɬɟɪɟ

ɩɨɜɟɞɟɧɢɹ ɫɢɫɬɟɦɵ ɭɠɟ ɩɪɨɢɫɯɨɞɹɬ ɪɚɡɢɬɟɥɶɧɵɟ ɩɟɪɟɦɟɧɵ ɢ ɜɨɡɧɢɤɚɟɬ

ɯɚɨɬɢɱɧɨɫɬɶ. ɑɬɨ ɠɟ ɤɚɫɚɟɬɫɹ ɚɧɚɥɢɡɚ ɧɟɥɢɧɟɣɧɵɯ ɹɜɥɟɧɢɣ, ɬɨ ɨɧ ɬɪɟɛɭɟɬ

ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɨɱɟɧɶ ɫɥɨɠɧɵɯ ɦɟɬɨɞɨɜ, ɜ ɨɫɨɛɟɧɧɨɫɬɢ ɤɨɝɞɚ ɡɚɞɚɱɚ ɯɚɪɚɤɬɟɪɢɡɭɟɬɫɹ

ɛɨɥɶɲɨɣ ɪɚɡɦɟɪɧɨɫɬɶɸ ɮɚɡɨɜɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ. ɉɨɬɨɦɭ ɛɵɥɨ ɛɵ ɠɟɥɚɬɟɥɶɧɨ

ɪɚɡɪɚɛɨɬɚɬɶ ɬɚɤɢɟ ɦɟɬɨɞɵ, ɤɨɬɨɪɵɟ ɫɜɨɞɢɥɢ ɛɵ ɡɚɞɚɱɭ ɜɵɫɨɤɨɣ ɪɚɡɦɟɪɧɨɫɬɢ ɤ ɛɨɥɟɟ

ɧɢɡɤɨɣ. ȼ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɫɢɫɬɟɦɚ ɛɥɢɡɤɚ ɤ ɬɨɱɤɟ, ɝɞɟ ɬɟɪɹɟɬɫɹ ɥɢɧɟɣɧɚɹ

ɭɫɬɨɣɱɢɜɨɫɬɶ, ɟɟ ɩɨɜɟɞɟɧɢɟ ɨɛɭɫɥɨɜɥɟɧɨ ɝɨɪɚɡɞɨ ɦɟɧɶɲɢɦ ɱɢɫɥɨɦ ɫɬɟɩɟɧɟɣ

ɫɜɨɛɨɞɵ, ɢ ɞɥɹ ɢɫɤɥɸɱɟɧɢɹ ɱɚɫɬɢ ɩɟɪɟɦɟɧɧɵɯ ɦɨɠɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɩɪɢɧɰɢɩ

ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ. ɋɯɨɠɢɟ ɢɞɟɢ ɦɵ ɦɨɠɟɦ ɧɚɣɬɢ ɬɚɤɠɟ ɜ ɬɟɨɪɟɦɟ ɨ ɰɟɧɬɪɚɥɶɧɨɦ

ɦɧɨɝɨɨɛɪɚɡɢɢ, ɯɨɬɹ ɩɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɹɜɥɹɟɬɫɹ ɛɨɥɟɟ ɨɛɳɢɦ. ȼ ɷɬɨɣ ɝɥɚɜɟ ɧɚɫ

ɛɭɞɟɬ ɢɧɬɟɪɟɫɨɜɚɬɶ ɬɚɤɠɟ ɪɨɥɶ ɫɤɨɪɨɫɬɟɣ ɭɫɬɚɧɨɜɥɟɧɢɹ ɷɤɨɧɨɦɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ

ɢ ɲɤɚɥɵ ɜɪɟɦɟɧɢ ɩɪɢ ɢɡɭɱɟɧɢɢ ɷɤɨɧɨɦɢɱɟɫɤɢɯ ɹɜɥɟɧɢɣ.

9.1 ɉɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ

ȼ ɷɬɨɦ ɪɚɡɞɟɥɟ ɦɵ ɨɛɴɹɫɧɢɦ ɩɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ ɏɚɤɟɧɚ, ɤɨɬɨɪɵɣ ɹɜɥɹɟɬɫɹ ɨɞɧɢɦ

ɢɡ ɨɫɧɨɜɨɩɨɥɚɝɚɸɳɢɯ ɦɟɬɨɞɨɜ ɜ ɫɢɧɟɪɝɟɬɢɤɟ. Ɋɚɫɫɦɨɬɪɢɦ ɫɩɟɪɜɚ ɩɪɨɫɬɨɣ ɩɪɢɦɟɪ,

ɞɚɧɧɵɣ ɏɚɤɟɧɨɦ (1977). ɉɭɫɬɶ ɞɢɧɚɦɢɱɟɫɤɚɹ ɫɢɫɬɟɦɚ ɫɨɫɬɨɢɬ ɢɡ ɞɜɭɯ ɭɪɚɜɧɟɧɢɣ

ɝɞɟ r

> 0. Ɉɱɟɜɢɞɧɨ, ɱɬɨ, ɧɟ ɛɭɞɶ ɭɪɚɜɧɟɧɢɹ (9.1.1), ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ

(9.1.2)

ɡɚɬɭɯɚɥɨ ɛɵ. ɉɨɬɪɟɛɭɟɦ r

฾r

. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɦɵ ɦɨɠɟɦ

ɩɪɢɛɥɢɠɟɧɧɨ ɪɟɲɢɬɶ ɭɪɚɜɧɟɧɢɟ (9.1.2), ɩɨɥɨɠɢɜ dy/dt = 0, ɱɬɨ ɩɪɢɜɟɞɟɬ ɤ

Ƚɨɜɨɪɹɬ, ɱɬɨ ɫɢɫɬɟɦɚ (9.1.2) ɩɨɞɱɢɧɟɧɚ ɫɢɫɬɟɦɟ (9.1.1). ɉɨɞɫɬɚɜɥɹɹ (9.1.3) ɜ

(9.1.1), ɩɨɥɭɱɢɦ

Ʌɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɬɨɝɨ, ɛɭɞɟɬ r

> 0 ɢɥɢ r

< 0, ɜ ɭɪɚɜɧɟɧɢɢ

dx/dt = 0 ɜɨɡɧɢɤɚɸɬ ɞɜɚ ɫɨɜɟɪɲɟɧɧɨ ɪɚɡɥɢɱɧɵɯ ɬɢɩɚ ɪɟɲɟɧɢɹ.

ȼ ɨɩɪɟɞɟɥɟɧɧɨɦ ɫɦɵɫɥɟ ɩɟɪɟɦɟɧɧɚɹ x ɨɩɢɫɵɜɚɟɬ ɫɬɟɩɟɧɶ «ɭɩɨ-

ɪɹɞɨɱɟɧɧɨɫɬɢ» ɫɥɨɠɧɨɣ ɫɢɫɬɟɦɵ. ɏɚɤɟɧ ɧɚɡɵɜɚɟɬ x «ɩɚɪɚɦɟɬɪɨɦ ɩɨɪɹɞɤɚ».

Ɍɨɥɶɤɨ ɱɬɨ ɩɪɨɞɟɦɨɧɫɬɪɢɪɨɜɚɧɧɚɹ ɬɟɯɧɢɤɚ ɢɫɤɥɸɱɟɧɢɹ ɛɵɫɬɪɨ ɭɛɵɜɚɸɳɢɯ

ɩɟɪɟɦɟɧɧɵɯ ɧɨɫɢɬ ɧɚɡɜɚɧɢɟ ɩɪɢɧɰɢɩɚ ɩɨɞɱɢɧɟɧɢɹ (ɚɞɢɚɛɚɬɢɱɟɫɤɨɣ

ɚɩɩɪɨɤɫɢɦɚɰɢɢ) ɏɚɤɟɧɚ. Ɉɛɨɫɧɨɜɚɧɢɟ ɷɬɨɝɨ ɦɟɬɨɞɚ ɛɵɥɨ ɩɪɨɜɟɞɟɧɨ ɜ ɪɚɛɨɬɟ

ɏɚɤɟɧɚ (1983)

Ⱦɥɹ ɨɛɨɛɳɟɧɢɹ ɩɪɟɞɵɞɭɳɟɣ ɫɢɫɬɟɦɵ ɪɚɫɫɦɨɬɪɢɦ

ɂɧɞɟɤɫɵ ɜ ɭɪɚɜɧɟɧɢɹɯ ɪɚɫɩɨɥɨɠɟɧɵ ɬɚɤɢɦ ɨɛɪɚɡɨɦ, ɱɬɨ ɩɟɪɟɦɟɧɧɵɟ

ɨɛɪɚɡɭɸɬ ɞɜɟ ɪɚɡɥɢɱɧɵɟ ɝɪɭɩɩɵ, ɩɪɢ ɷɬɨɦ ɧɨɦɟɪɚ i = 1,..., m ɨɬɧɨɫɹɬɫɹ ɤ

ɦɨɞɚɦ ɫɨ ɫɥɚɛɵɦ ɡɚɬɭɯɚɧɢɟɦ ɚɦɩɥɢɬɭɞɵ, ɤɨɬɨɪɵɟ ɦɨɝɭɬ ɛɵɬɶ ɧɟɭɫɬɨɣɱɢɜɵ

(ɬ. ɟ. r

ɦɨɠɟɬ ɛɵɬɶ ɧɟɩɨɥɨɠɢɬɟɥɶɧɵɦ), ɚ ɧɨɦɟɪɚ i = ɬ + 1,..., n ɨɬɧɨɫɹɬɫɹ ɤ

ɭɫɬɨɣɱɢɜɵɦ ɦɨɞɚɦ. Ɏɭɧɤɰɢɢ J

ɹɜɥɹɸɬɫɹ ɧɟɥɢɧɟɣɧɵɦɢ ɮɭɧɤɰɢɹɦɢ ɫɜɨɢɯ

ɚɪɝɭɦɟɧɬɨɜ.

ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɨɩɢɫɵɜɚɟɦɚɹ ɩɪɨɰɟɞɭɪɚ ɦɨɠɟɬ ɛɵɬɶ ɩɪɢɦɟɧɟɧɚ ɤ

ɧɟɥɢɧɟɣɧɨɣ ɫɢɫɬɟɦɟ ɨɛɳɟɝɨ ɜɢɞɚ

Ɂɧɚɱɢɬɟɥɶɧɨ ɪɚɧɶɲɟ ɷɬɨɬ ɪɟɡɭɥɶɬɚɬ ɛɵɥ ɩɨɥɭɱɟɧ ɜ ɪɚɛɨɬɚɯ

Ⱥ. ɇ. Ɍɢɯɨɧɨɜɚ (ɫɦ., ɧɚɩɪɢɦɟɪ, Ɍɢɯɨɧɨɜ Ⱥ. ɇ. «Ɉ ɡɚɜɢɫɢɦɨɫɬɢ

ɪɟɲɟɧɢɣ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɯ ɭɪɚɜɧɟɧɢɣ ɨɬ ɦɚɥɨɝɨ ɩɚɪɚɦɟɬɪɚ»,

Ɇɚɬɟɦɚɬɢɱ. ɫɛɨɪɧɢɤ, 1948, ɬ. 22(64), ɜɵɩ. 2, ɫ. 193-204 ɢ ɪɹɞ

ɩɨɫɥɟɞɭɸɳɢɯ ɪɚɛɨɬ). ȼ ɨɬɟɱɟɫɬɜɟɧɧɨɣ ɥɢɬɟɪɚɬɭɪɟ ɨɧ ɢɡɜɟɫɬɟɧ

ɤɚɤ ɬɟɨɪɟɦɚ Ɍɢɯɨɧɨɜɚ (ɫɦ. ɨɛ ɷɬɨɦ, ɧɚɩɪɢɦɟɪ, ȼɚɫɢɥɶɟɜɚ Ⱥ. Ȼ.,

Ȼɭɬɭɡɨɜ ȼ. ĭ.Ț Ⱥɫɢɦɩɬɨɬɢɱɟɫɤɢɟ ɦɟɬɨɞɵ ɜ ɬɟɨɪɢɢ ɫɢɧɝɭɥɹɪɧɵɯ

ɜɨɡɦɭɳɟɧɢɣ,

M.: ȼɵɫɲɚɹ ɲɤɨɥɚ, 1990, 208 ɫ.). — ɉɪɢɦ. ɪɟɞ.