Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории

Подождите немного. Документ загружается.

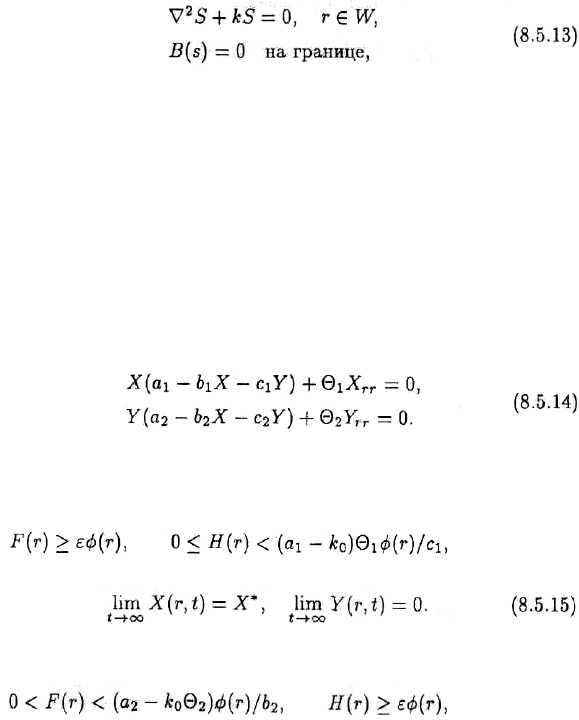
ɋɮɨɪɦɭɥɢɪɭɟɦ ɡɚɞɚɱɭ ɧɚ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ

ɝɞɟ k — ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ, a S — ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɫɨɛɫɬɜɟɧɧɵɣ ɜɟɤɬɨɪ. ɗɬɨ ɭɪɚɜɧɟɧɢɟ ɜ

ɱɚɫɬɧɵɯ ɩɪɨɢɡɜɨɞɧɵɯ ɪɚɡɦɟɪɧɨɫɬɢ 1, ɢ ɪɟɲɟɧɢɟ ɟɝɨ ɯɨɪɨɲɨ ɢɡɜɟɫɬɧɨ. Ɉɛɨɡɧɚɱɢɦ

ɧɚɢɦɟɧɶɲɟɟ ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ ɤɚɤ k

, ɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɫɨɛɫɬɜɟɧɧɵɣ ɜɟɤɬɨɪ ɤɚɤ

(r).

Ɉɬɧɨɪɦɢɪɭɟɦ ɷɬɨɬ ɜɟɤɬɨɪ ɬɚɤ, ɱɬɨ max

(r)= 1. Ɇɨɠɧɨ ɩɪɨɜɟɪɢɬɶ, ɱɬɨ k

(r)ɩɨɥɨɠɢɬɟɥɶɧɵ.

Ɍɟɨɪɟɦɚ 8.5.3. ɉɭɫɬɶ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ ɡɚɞɚɱɢ (8.5.3) ɹɜɥɹɸɬɫɹ ɭɫɥɨɜɢɹ (8.5.12).

Ɍɨɝɞɚ ɬɪɢɜɢɚɥɶɧɨɟ ɪɟɲɟɧɢɟ (0,0) ɡɚɞɚɱɢ (8.5.3) ɚɫɢɦɩɬɨɬɢɱɟɫɤɢ ɭɫɬɨɣɱɢɜɨ ɜ ɝɥɨɛɚɥɶɧɨɦ

ɫɦɵɫɥɟ (ɨɬɧɨɫɢɬɟɥɶɧɨ ɧɟɨɬɪɢɰɚɬɟɥɶɧɵɯ ɜɨɡɦɭɳɟɧɢɣ), ɟɫɥɢ α

< k

, α

< k

, ɢ

ɧɟɭɫɬɨɣɱɢɜɨ, ɟɫɥɢ α

> k

ɢɥɢ α

> k

ȿɫɥɢ ɟɦɤɨɫɬɶ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɫɥɢɲɤɨɦ ɦɚɥɚ, ɜ ɧɟɦ ɧɟ ɩɨɦɟɫɬɢɬɫɹ ɧɢɤɚɤɚɹ

ɝɪɭɩɩɚ. ɍɫɥɨɜɢɟ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɩɪɨɢɡɜɨɥɶɧɨɟ ɦɚɥɨɟ ɜɨɡɦɭɳɟɧɢɟ

ɬɪɢɜɢɚɥɶɧɨɝɨ ɪɟɲɟɧɢɹ ɩɪɢɜɟɞɟɬ ɤ ɧɨɜɨɣ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɟ. Ʉɨɧɟɱɧɨ, ɧɚɫ ɢɧɬɟɪɟɫɭɟɬ

ɬɨɥɶɤɨ ɫɥɭɱɚɣ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ ɬɪɢɜɢɚɥɶɧɨɝɨ ɪɟɲɟɧɢɹ. Ɋɚɜɧɨɜɟɫɢɟ ɫɢɫɬɟɦɵ (8.5.1)

ɨɩɪɟɞɟɥɹɟɬɫɹ ɤɚɤ ɪɟɲɟɧɢɟ ɫɢɫɬɟɦɵ ɭɪɚɜɧɟɧɢɣ

Ɍɟɨɪɟɦɚ 8.5.4. ɉɭɫɬɶ ɫɢɫɬɟɦɚ (8.5.3) ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ (8.5.12). Ɍɨɝɞɚ

i) ȿɫɥɢ α

> k

ɢ α

< k

, ɬɨ ɫɢɫɬɟɦɚ (8.5.14) ɢɦɟɟɬ ɟɞɢɧɫɬɜɟɧɧɨɟ ɩɨɥɨɠɢɬɟɥɶɧɨɟ

ɪɟɲɟɧɢɟ (X

(r), 0); ɢ ɞɥɹ ɥɸɛɨɣ ɩɚɪɵ ɧɚɱɚɥɶɧɵɯ ɮɭɧɤɰɢɣ (F, H), ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɯ

ɭɫɥɨɜɢɹɦ

ɝɞɟ İ ɦɨɠɟɬ ɛɵɬɶ ɩɪɨɢɡɜɨɥɶɧɨ ɦɚɥɵɦ, ɪɟɲɟɧɢɟ (8.5.3) ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɫɥɨɜɢɹɦ

ii) ȿɫɥɢ α

> k

ɢ α

> k

ɬɨ ɫɢɫɬɟɦɚ (8.5.13) ɨɛɥɚɞɚɟɬ ɩɨɥɨɠɢɬɟɥɶɧɵɦ ɪɟɲɟɧɢɟɦ (0, Y

(r)), ɢ ɞɥɹ ɥɸɛɨɣ ɩɚɪɵ ɧɚɱɚɥɶɧɵɯ ɮɭɧɤɰɢɣ (F, H), ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɯ ɭɫɥɨɜɢɹɦ

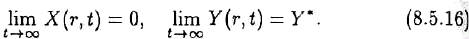
ɝɞɟ İ ɦɨɠɟɬ ɛɵɬɶ ɩɪɨɢɡɜɨɥɶɧɨ ɦɚɥɵɦ, ɪɟɲɟɧɢɟ ɫɢɫɬɟɦɵ (8.5.3) ɭɞɨɜɥɟɬɜɨɪɹɟɬ

ɭɫɥɨɜɢɹɦ

Ɍɚɤ ɤɚɤ α

> k

, ɭɫɥɨɜɢɟ α

< k

ɜ ɩɭɧɤɬɟ (i) ɦɨɠɧɨ ɩɟɪɟɩɢɫɚɬɶ ɜ ɜɢɞɟ Θ

< a/k

; ɷɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɜɦɟɫɬɢɦɨɫɬɶ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ ɨɝɪɚɧɢɱɟɧɚ ɫɜɟɪɯɭ

ɯɚɪɚɤɬɟɪɢɫɬɢɤɨɣ ɝɪɭɩɩɵ 1 ɢ ɫɧɢɡɭ — ɝɪɭɩɩɵ 2. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɝɪɭɩɩɚ 2 ɫ ɬɟɱɟɧɢɟɦ ɜɪɟɦɟɧɢ

ɜɵɬɢɫɧɢɬɫɹ ɝɪɭɩɩɨɣ 1.

ɇɚɤɨɧɟɰ, ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɟɫɥɢ α

> k

ɬɨ ɩɪɢ ɩɨɞɯɨɞɹɳɢɯ ɧɚɱɚɥɶɧɵɯ

ɭɫɥɨɜɢɹɯ ɜ ɫɢɫɬɟɦɟ ɦɨɝɭɬ ɫɨɫɭɳɟɫɬɜɨɜɚɬɶ ɨɛɟ ɝɪɭɩɩɵ. əɜɧɵɣ ɜɢɞ ɬɚɤɢɯ ɧɚɱɚɥɶɧɵɯ ɭɫɥɨɜɢɣ

ɦɨɠɧɨ ɧɚɣɬɢ ɜ ɪɚɛɨɬɟ Ɂɚɧɝɚ (1989ɫ).

8.6 ɍɪɛɚɧɢɫɬɢɱɟɫɤɢɟ ɨɛɪɚɡɨɜɚɧɢɹ

ɬɢɩɚ ɛɟɝɭɳɢɯ ɜɨɥɧ

ȼ ɩɪɟɞɵɞɭɳɢɯ ɪɚɡɞɟɥɚɯ ɦɵ ɚɧɚɥɢɡɢɪɨɜɚɥɢ ɪɚɡɧɨɨɛɪɚɡɧɵɟ ɩɪɨɛɥɟɦɵ ɝɪɚɞɨɮɨɪɦɢɪɨɜɚɧɢɹ.

Ȼɵɥɨ ɩɨɤɚɡɚɧɨ, ɱɬɨ ɱɢɫɥɨ ɜɨɡɦɨɠɧɵɯ ɮɨɪɦ ɝɨɪɨɞɫɤɢɯ ɫɬɪɭɤɬɭɪ ɜ ɫɬɪɭɤɬɭɪɧɨ ɭɫɬɨɣɱɢɜɵɯ

ɫɢɫɬɟɦɚɯ ɞɨɜɨɥɶɧɨ ɨɝɪɚɧɢɱɟɧɨ. ɇɟɭɫɬɨɣɱɢɜɨɫɬɶ ɭɜɟɥɢɱɢɜɚɟɬ ɪɚɡɧɨɨɛɪɚɡɢɟ ɝɨɪɨɞɫɤɢɯ

ɫɬɪɭɤɬɭɪ. ɑɬɨɛɵ ɩɪɨɢɥɥɸɫɬɪɢɪɨɜɚɬɶ, ɤɚɤ ɢɦɟɧɧɨ ɧɟɭɫɬɨɣɱɢɜɨɫɬɶ ɦɨɠɟɬ ɭɫɥɨɠɧɢɬɶ

ɝɨɪɨɞɫɤɭɸ ɫɢɫɬɟɦɭ, ɦɵ ɪɚɫɫɦɨɬɪɢɦ ɦɨɞɟɥɶ ɝɨɪɨɞɚ, ɤɨɬɨɪɚɹ ɜɛɥɢɡɢ ɧɟɭɫɬɨɣɱɢɜɵɯ ɨɫɨɛɵɯ

ɬɨɱɟɤ ɜɟɞɟɬ ɫɟɛɹ ɩɨɞɨɛɧɨ ɛɟɝɭɳɟɣ ɜɨɥɧɟ. ɗɬɚ

ɦɨɞɟɥɶ ɛɵɥɚ ɩɪɟɞɥɨɠɟɧɚ ɚɜɬɨɪɨɦ ɤɧɢɝɢ (Ɂɚɧɝ,

1989ɟ).

Ƚɟɨɝɪɚɮɢɱɟɫɤɢɟ ɯɚɪɚɤɬɪɢɫɬɢɤɢ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɝɨɪɨɞɫɤɨɣ ɫɢɫɬɟɦɵ ɩɨɞɨɛɧɵ ɬɟɦ, ɱɬɨ

ɩɪɢɜɟɞɟɧɵ ɜ ɪɚɡɞ. 8.4. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɦɨɞɟɥɶ ɨɩɢɫɵɜɚɟɬɫɹ ɞɜɭɦɹ ɩɟɪɟɦɟɧɧɵɦɢ:

n(r,t) — ɩɥɨɬɧɨɫɬɶ ɧɚɫɟɥɟɧɢɹ ɜ ɬɨɱɤɟ (r,t);

q(r,t) — ɤɚɱɟɫɬɜɨ ɠɢɥɢɳɧɨɝɨ ɮɨɧɞɚ ɜ ɬɨɱɤɟ (r,t),

ɝɞɟ r — ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɐȾɊ ɞɨ ɦɟɫɬɚ ɩɪɨɠɢɜɚɧɢɹ.

ɋɥɟɞɭɟɬ ɩɨɞɱɟɪɤɧɭɬɶ, ɨɞɧɚɤɨ; ɱɬɨ ɦɨɞɟɥɶ

, ɨɛɫɭɠɞɚɟɦɚɹ ɜ ɪɚɡɞ. 8.4, ɤɚɫɚɟɬɫɹ ɢɧɵɯ

ɚɫɩɟɤɬɨɜ ɩɪɨɰɟɫɫɚ ɮɨɪɦɢɪɨɜɚɧɢɹ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ, ɧɟɠɟɥɢ ɬɚ ɦɨɞɟɥɶ, ɤɨɬɨɪɭɸ ɦɵ

ɛɭɞɟɦ ɫɬɪɨɢɬɶ ɡɞɟɫɶ.

ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɜ ɬɟɱɟɧɢɟ ɢɡɭɱɚɟɦɨɝɨ ɩɟɪɢɨɞɚ ɱɢɫɥɟɧɧɨɫɬɶ ɧɚɫɟɥɟɧɢɹ ɧɟ ɢɡɦɟɧɹɟɬɫɹ.

Ɇɵ ɩɪɟɧɟɛɪɟɝɚɟɦ ɞɟɦɨɝɪɚɮɢɱɟɫɤɢɦɢ ɩɪɨɰɟɫɫɚɦɢ ɢ ɩɪɨɰɟɫɫɚɦɢ ɦɢɝɪɚɰɢɢ ɦɟɠɞɭ ɝɨɪɨɞɨɦ ɢ

«ɜɧɟɲɧɢɦ ɦɢɪɨɦ». ɋɨɝɥɚɫɧɨ ɪɚɛɨɬɟ Ɂɚɧɝɚ (1989ɟ), ɝɨɪɨɞɫɤɚɹ ɫɢɫɬɟɦɚ ɨɩɢɫɵɜɚɟɬɫɹ

ɫɥɟɞɭɸɳɢɦɢ ɞɢɧɚɦɢɱɟɫɤɢɦɢ ɭɪɚɜɧɟɧɢɹɦɢ

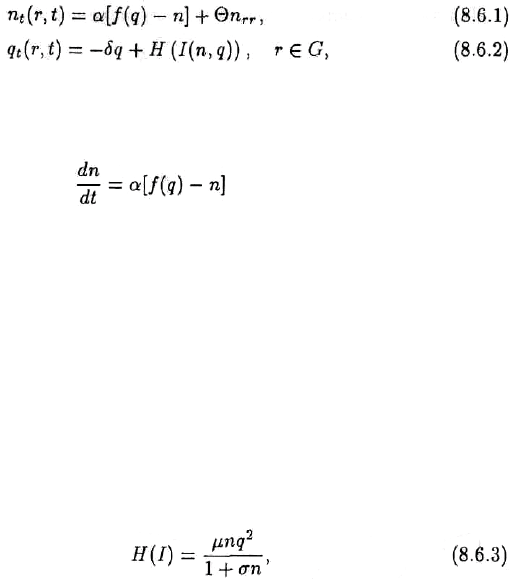
ɝɞɟ G ɨɛɨɡɧɚɱɚɟɬ ɨɛɥɚɫɬɶ ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ, ɚ — ɩɚɪɚɦɟɬɪ ɚɞɚɩɬɚɰɢɢ, Θ ɢ δ —

ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɩɚɪɚɦɟɬɪ ɞɢɮɮɭɡɢɢ ɧɚɫɟɥɟɧɢɹ ɢ ɫɤɨɪɨɫɬɶ ɪɚɡɪɭɲɟɧɢɹ ɠɢɥɨɝɨ ɮɨɧɞɚ.

ɋɢɫɬɟɦɚ ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɨɩɪɟɞɟɥɟɧɧɵɦ ɧɚɱɚɥɶɧɵɦ ɢ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ. Ⱦɢɮɮɭɡɢɨɧɧɵɟ

ɷɮɮɟɤɬɵ ɢɡɦɟɧɟɧɢɹ ɤɚɱɟɫɬɜɚ ɠɢɥɶɹ ɨɬɫɭɬɫɬɜɭɸɬ.

Ⱦɥɹ ɢɧɬɟɪɩɪɟɬɚɰɢɢ (8.6.1) ɨɩɭɫɬɢɦ ɞɢɮɮɭɡɢɨɧɧɵɣ ɱɥɟɧ. ɂɬɚɤ, ɢɦɟɟɦ

ɋɱɢɬɚɟɬɫɹ, ɱɬɨ ɜɢɞ ɮɭɧɤɰɢɢ f(q) ɦɨɠɧɨ ɧɚɣɬɢ ɢɡ ɩɪɟɞɩɨɥɨɠɟɧɢɹ ɪɚɰɢɨɧɚɥɶɧɨɫɬɢ ɩɨɜɟɞɟɧɢɹ

ɞɨɦɨɯɨɡɹɣɫɬɜ. ɗɬɚ ɮɭɧɤɰɢɹ ɨɩɪɟɞɟɥɹɟɬ ɪɚɜɧɨɜɟɫɧɨɟ ɡɧɚɱɟɧɢɟ ɩɥɨɬɧɨɫɬɢ ɧɚɫɟɥɟɧɢɹ ɩɪɢ

ɡɚɞɚɧɧɨɦ ɤɚɱɟɫɬɜɟ ɠɢɥɨɝɨ ɮɨɧɞɚ.

ɍɪɚɜɧɟɧɢɟ (8.6.2) ɨɩɢɫɵɜɚɟɬ, ɤɚɤ ɤɚɱɟɫɬɜɨ ɠɢɥɶɹ ɢɡɦɟɧɹɟɬɫɹ ɜɨ ɜɪɟɦɟɧɢ. ɑɥɟɧ —

ɨɩɢɫɵɜɚɟɬ ɷɮɮɟɤɬɵ ɪɚɡɪɭɲɟɧɢɹ ɠɢɥɨɝɨ ɮɨɧɞɚ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɫɨɫɬɨɹɧɢɟ ɠɢɥɢɳ

ɩɨɞɞɟɪɠɢɜɚɟɬɫɹ ɜɥɚɞɟɥɶɰɚɦɢ, ɤɨɬɨɪɵɟ ɨɩɪɟɞɟɥɹɸɬ ɜɟɥɢɱɢɧɭ ɪɚɫɯɨɞɨɜ ɧɚ ɫɨɞɟɪɠɚɧɢɟ ɠɢɥɨɝɨ

ɮɨɧɞɚ, ɢ ɫɬɨɢɦɨɫɬɶ ɠɢɥɶɹ ɡɚɜɢɫɢɬ ɨɬ ɞɨɯɨɞɚ ɜɥɚɞɟɥɶɰɚ ɫ ɟɞɢɧɢɰɵ ɠɢɥɨɝɨ ɮɨɧɞɚ. ɉɭɫɬɶ

ɨɛɳɢɣ ɞɨɯɨɞ ɨɛɨɡɧɚɱɟɧ ɤɚɤ I. Ⱦɨɯɨɞ ɜ ɨɩɪɟɞɟɥɟɧɧɨɣ ɬɨɱɤɟ ɡɚɜɢɫɢɬ ɨɬ ɩɥɨɬɧɨɫɬɢ ɧɚɫɟɥɟɧɢɹ ɢ

ɤɚɱɟɫɬɜɚ ɠɢɥɨɝɨ ɮɨɧɞɚ, ɬ. ɟ.

I = I(n, q), ɩɪɢɱɟɦ ɩɪɨɢɡɜɨɞɧɚɹ I

ɷɬɨɝɨ ɮɭɧɤɰɢɨɧɚɥɚ

ɡɧɚɤɨɧɟɨɩɪɟɞɟɥɟɧɚ, ɚ ɩɪɨɢɡɜɨɞɧɚɹ I

ɩɨɥɨɠɢɬɟɥɶɧɚ. Ɂɧɚɤ I

ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɩɪɢ

ɮɢɤɫɢɪɨɜɚɧɧɨɦ ɭɪɨɜɧɟ q ɧɟ ɨɩɪɟɞɟɥɟɧ, ɬɚɤ ɤɚɤ ɭɜɟɥɢɱɟɧɢɟ ɥɢɛɨ ɭɦɟɧɶɲɟɧɢɟ ɞɨɯɨɞɚ ɩɪɢ

ɭɜɟɥɢɱɟɧɢɢ ɩɥɨɬɧɨɫɬɢ ɧɚɫɟɥɟɧɢɹ ɡɚɜɢɫɢɬ ɨɬ ɤɨɧɤɪɟɬɧɨɣ ɫɢɬɭɚɰɢɢ. ɉɪɨɢɡɜɨɞɧɚɹ I

ɩɨɥɨɠɢɬɟɥɶɧɚ, ɩɨɬɨɦɭ ɱɬɨ ɭɥɭɱɲɟɧɢɟ ɤɚɱɟɫɬɜɚ ɠɢɥɶɹ ɩɪɢ ɮɢɤɫɢɪɨɜɚɧɧɨɦ ɭɪɨɜɧɟ ɩɥɨɬɧɨɫɬɢ

ɧɚɫɟɥɟɧɢɹ ɞɨɥɠɧɨ ɩɪɢɜɟɫɬɢ ɤ ɜɨɡɪɚɫɬɚɧɢɸ ɞɨɯɨɞɚ ɜɥɚɞɟɥɶɰɚ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɡɚɬɪɚɬɵ ɧɚ

ɩɨɞɞɟɪɠɚɧɢɟ ɠɢɥɨɝɨ ɮɨɧɞɚ ɩɨɥɨɠɢɬɟɥɶɧɨ ɫɜɹɡɚɧɵ ɫ ɞɨɯɨɞɨɦ, ɬ. ɟ. dH/dI > 0. Ⱦɥɹ ɩɪɨɫɬɨɬɵ

ɦɵ ɨɩɪɟɞɟɥɢɦ ɮɭɧɤɰɢɸ ɡɚɬɪɚɬ ɧɚ ɩɨɞɞɟɪɠɚɧɢɟ ɠɢɥɨɝɨ ɮɨɧɞɚ ɤɚɤ

ɝɞɟ ȝ ɢ ı — ɩɨɥɨɠɢɬɟɥɶɧɵɟ ɤɨɷɮɮɢɰɢɟɧɬɵ. ȿɫɥɢ ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ q

/(l + ın) ɤɚɤ ɪɟɧɬɭ

ɟɞɢɧɢɰɵ ɠɢɥɨɝɨ ɮɨɧɞɚ, ɬɨ ɜɟɥɢɱɢɧɚ nq

/(1+ın) ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɩɨɥɧɵɣ ɞɨɯɨɞ

ɞɨɦɨɜɥɚɞɟɥɶɰɚ ɜ ɞɚɧɧɨɣ ɬɨɱɤɟ. ɉɚɪɚɦɟɬɪ ȝ ɦɨɠɧɨ ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ ɤɚɤ ɨɬɧɨɲɟɧɢɟ ɡɚɬɪɚɬ ɧɚ

ɩɨɞɞɟɪɠɚɧɢɟ ɮɨɧɞɚ ɤ ɨɛɳɟɦɭ ɞɨɯɨɞɭ.

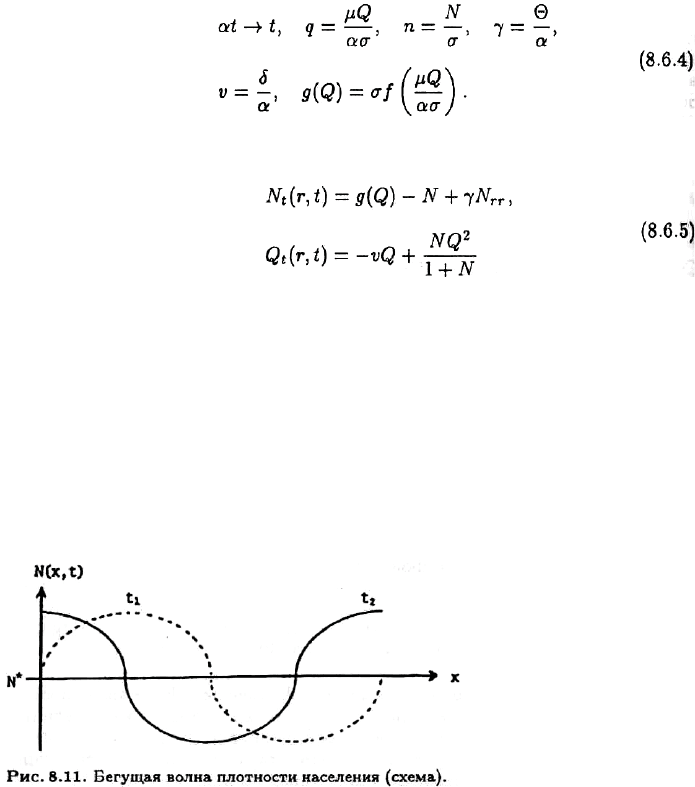
Ⱦɥɹ ɚɧɚɥɢɡɚ ɫɢɫɬɟɦɵ ɩɪɨɜɟɞɟɦ ɫɥɟɞɭɸɳɢɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ:

ȼ ɪɟɡɭɥɶɬɚɬɟ ɫɢɫɬɟɦɚ (8.6.1)-(8.6.2) ɦɨɠɟɬ ɛɵɬɶ ɡɚɩɢɫɚɧɚ ɤɚɤ

ɫ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦɢ ɧɚɱɚɥɶɧɵɦɢ ɢ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ. Ɇɵ ɩɪɟɞɩɨɥɚɝɚɟɦ, ɱɬɨ ɜ ɫɢɫɬɟɦɟ

(8.6.5) ɚɫɢɦɩɬɨɬɢɱɟɫɤɨɟ ɪɚɜɧɨɜɟɫɢɟ ɫɭɳɟɫɬɜɭɟɬ. ɇɚɫ ɢɧɬɟɪɟɫɭɟɬ ɫɭɳɟɫɬɜɨɜɚɧɢɟ

ɩɟɪɢɨɞɢɱɟɫɤɢɯ ɪɟɲɟɧɢɣ ɬɢɩɚ ɛɟɝɭɳɢɯ ɜɨɥɧ ɜɛɥɢɡɢ ɚɫɢɦɩɬɨɬɢɱɟɫɤɨɝɨ ɫɬɚɬɢɱɟɫɤɨɝɨ ɪɚɜɧɨɜɟ-

ɫɢɹ. Ⱦɥɹ ɪɟɲɟɧɢɹ ɷɬɨɣ ɡɚɞɚɱɢ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɬɟɨɪɢɟɣ ɛɢɮɭɪɤɚɰɢɣ.

ɉɟɪɢɨɞɢɱɟɫɤɢɟ ɪɟɲɟɧɢɹ ɬɢɩɚ ɛɟɝɭɳɢɯ ɜɨɥɧ ɨɛɵɱɧɵ ɞɥɹ ɭɪɚɜɧɟɧɢɣ ɜ ɱɚɫɬɧɵɯ

ɩɪɨɢɡɜɨɞɧɵɯ ɢ ɱɚɫɬɨ ɧɚɛɥɸɞɚɸɬɫɹ ɜ ɮɢɡɢɤɟ

, ɯɢɦɢɢ ɢ ɛɢɨɥɨɝɢɢ. ɉɨɞɨɛɧɨɟ ɩɨɜɟɞɟɧɢɟ ɦɨɠɧɨ

ɩɪɨɢɥɥɸɫɬɪɢɪɨɜɚɬɶ ɫɯɟɦɨɣ, ɩɪɢɜɟɞɟɧɧɨɣ ɧɚ ɪɢɫ. 8.11. ȿɫɥɢ ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ ɬɚɤɨɟ

ɩɨɜɟɞɟɧɢɟ ɤɚɤ ɷɜɨɥɸɰɢɸ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ ɜ ɩɪɨɫɬɪɚɧɫɬɜɟ, ɬɨ ɜɢɞɧɨ, ɱɬɨ ɜ ɧɚɱɚɥɶɧɨɣ

ɫɬɚɞɢɢ ɧɚɢɛɨɥɟɟ ɩɥɨɬɧɨ ɡɚɫɟɥɟɧɧɨɟ ɩɪɨɫɬɪɚɧɫɬɜɨ, ɬ. ɟ. ɩɪɨɫɬɪɚɧɫɬɜɨ ɫ ɧɚɢɛɨɥɶɲɟɣ

ɪɚɡɧɨɫɬɶɸ ɦɟɠɞɭ ɪɟɚɥɶɧɨɣ ɢ ɪɚɜɧɨɜɟɫɧɨɣ ɩɥɨɬɧɨɫɬɶɸ, ɪɚɫɩɨɥɚɝɚɟɬɫɹ ɜɛɥɢɡɢ ɐȾɊ. ɋ ɬɟɱɟ-

ɧɢɟɦ ɜɪɟɦɟɧɢ ɧɚɢɛɨɥɟɟ

ɩɥɨɬɧɨ ɡɚɫɟɥɟɧɧɨɟ ɩɪɨɫɬɪɚɧɫɬɜɨ ɭɞɚɥɹɟɬɫɹ ɨɬ ɐȾɊ, ɢ ɩɨɡɠɟ

ɧɚɢɛɨɥɶɲɭɸ ɩɥɨɬɧɨɫɬɶ ɦɨɠɧɨ ɨɛɧɚɪɭɠɢɬɶ ɨɤɨɥɨ ɫɟɪɟɞɢɧɵ ɩɪɢɥɟɝɚɸɳɟɝɨ ɤ ɰɟɧɬɪɭ

ɝɨɪɨɞɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɚ.

Ɋɟɲɟɧɢɟ ɫɢɫɬɟɦɵ (8.6.5) ɬɢɩɚ ɛɟɝɭɳɟɣ ɜɨɥɧɵ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ

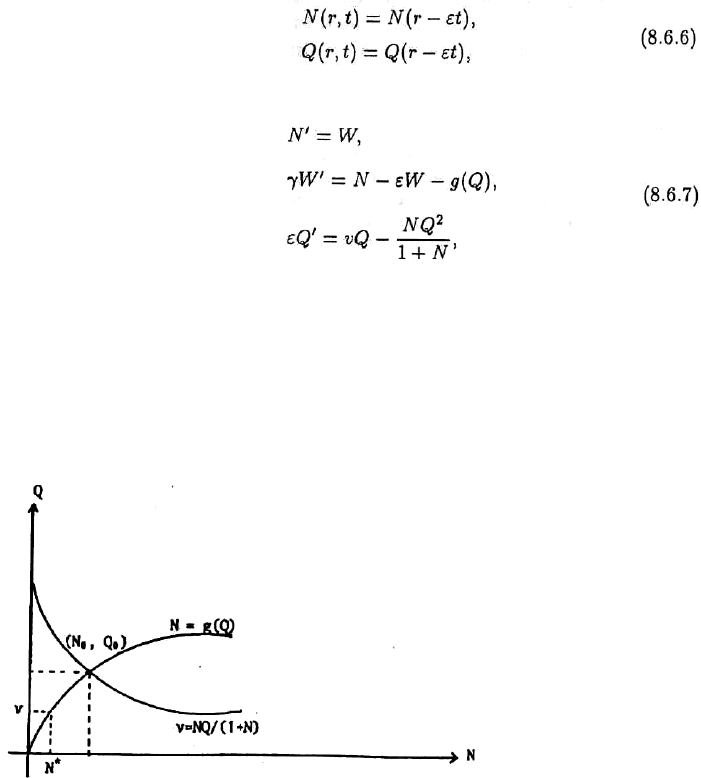
ɝɞɟ İ — ɩɨɥɨɠɢɬɟɥɶɧɵɣ ɩɚɪɚɦɟɬɪ, ɤɨɬɨɪɵɣ ɧɭɠɧɨ ɟɳɟ ɨɩɪɟɞɟɥɢɬɶ. ɉɟɪɢɨɞɢɱɟɫɤɚɹ ɝɨɪɨɞɫɤɚɹ

ɫɬɪɭɤɬɭɪɚ ɬɢɩɚ ɛɟɝɭɳɟɣ ɜɨɥɧɵ ɨɩɪɟɞɟɥɹɟɬɫɹ ɤɚɤ ɪɟɲɟɧɢɟ, ɩɟɪɢɨɞɢɱɟɫɤɨɟ ɨɬɧɨɫɢɬɟɥɶɧɨ r - İt.

ȼɜɟɞɹ ɮɭɧɤɰɢɸ W(r - İt) = N'(r - İt) ɢ ɩɨɞɫɬɚɜɢɜ (8.6.6) ɜ (8.6.5), ɦɵ ɩɨɥɭɱɢɦ

ɝɞɟ ɲɬɪɢɯ ɨɡɧɚɱɚɟɬ ɩɪɨɢɡɜɨɞɧɭɸ ɩɨ (r- İt). Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɧɚɲɚ ɡɚɞɚɱɚ ɫɜɨɞɢɬɫɹ ɤ

ɞɨɤɚɡɚɬɟɥɶɫɬɜɭ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɩɪɟɞɟɥɶɧɨɝɨ ɰɢɤɥɚ ɜ ɫɢɫɬɟɦɟ (8.6.7). Ɂɞɟɫɶ ɩɪɢɦɟɧɢɦɚ ɬɟɨɪɟɦɚ

ɏɨɩɮɚ ɨ ɛɢɮɭɪɤɚɰɢɹɯ.

Ʉɚɤ ɩɨɤɚɡɚɧɨ ɜ ɪɚɛɨɬɟ ɚɜɬɨɪɚ (Ɂɚɧɝ, 1989ɟ), ɪɚɜɧɨɜɟɫɢɟ ɜ ɫɢɫɬɟɦɟ (8.6.7) — ɤɨɬɨɪɨɟ

ɨɛɨɡɧɚɱɢɦ ɞɚɥɟɟ ɤɚɤ (N

, W

, Q

), ɝɞɟ W

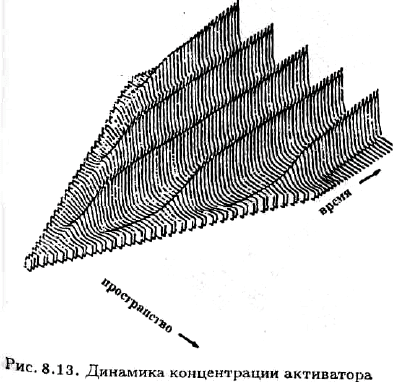
= 0, — ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɫɯɟɦɟ, ɢɡɨɛɪɚɠɟɧɧɨɣ ɧɚ ɪɢɫ.

8.12.

Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɩɪɟɞɟɥɶɧɵɯ ɰɢɤɥɨɜ ɦɨɠɧɨ ɩɪɨɜɟɫɬɢ, ɢɫɩɨɥɶɡɭɹ ɦɟɬɨɞ

ɬɟɨɪɢɢ ɛɢɮɭɪɤɚɰɢɣ, ɨɩɢɫɚɧɧɵɣ ɜ ɝɥ. 5. ȼ ɪɚɛɨɬɟ Ɂɚɧɝɚ (1989ɟ) ɞɨɤɚɡɚɧɚ ɫɥɟɞɭɸɳɚɹ ɬɟɨɪɟɦɚ:

Ɍɟɨɪɟɦɚ 8.6.1. ɂɦɟɟɬɫɹ ɧɟɩɭɫɬɨɟ ɦɧɨɠɟɫɬɜɨ ɡɧɚɱɟɧɢɣ ɩɚɪɚɦɟɬɪɨɜ, ɩɪɢ ɤɨɬɨɪɵɯ ɜ ɫɢɫɬɟɦɟ

(8.6.7) ɫɭɳɟɫɬɜɭɟɬ ɩɟɪɢɨɞɢɱɟɫɤɚɹ

Ɋɢɫ. 8.12. ɋɭɳɟɫɬɜɨɜɚɧɢɟ ɟɞɢɧɫɬɜɟɧɧɨɝɨ ɩɨɥɨɠɢɬɟɥɶɧɨɝɨ ɪɚɜɧɨɜɟɫɢɹ.

ɜɢɞɟ

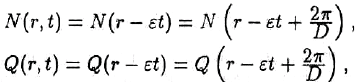
ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ ɬɢɩɚ ɛɟɝɭɳɟɣ ɜɨɥɧɵ ɜɢɞɚ

ɝɞɟ D ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɚɪɚɦɟɬɪɚɦɢ ɡɚɞɚɱɢ, ɚ İ ɞɨɫɬɚɬɨɱɧɨ ɦɚɥɨ.

ɋɥɟɞɭɟɬ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɜ ɤɚɱɟɫɬɜɟ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ ɦɵ ɜɵɛɪɚɥɢ ɩɚɪɚɦɟɬɪ Ȟ. ɉɨɫɤɨɥɶɤɭ Ȟ

= δ/ɚ, ɡɧɚɱɟɧɢɟ ɷɬɨɝɨ ɩɚɪɚɦɟɬɪɚ ɦɨɠɟɬ ɛɵɬɶ ɢɡɦɟɧɟɧɨ ɥɢɛɨ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɮɚɤɬɨɪɚ ɢɡɧɨɫɚ

ɠɢɥɨɝɨ ɮɨɧɞɚ, ɥɢɛɨ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɫɤɨɪɨɫɬɢ ɭɫɬɚɧɨɜɥɟɧɢɹ ɜ ɭɪɚɜɧɟɧɢɢ ɞɥɹ ɩɥɨɬɧɨɫɬɢ

ɧɚɫɟɥɟɧɢɹ. Ʉɚɤ ɫɤɚɡɚɧɨ ɜ

ɪɚɛɨɬɟ Ɂɚɧɝɚ (1989ɟ), ɬɟɨɪɟɦɚ ɭɬɜɟɪɠɞɚɟɬ, ɱɬɨ ɩɪɢ ɦɚɥɨɦ

ɜɨɡɦɭɳɟɧɢɢ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ ɩɚɪɚɦɟɬɪɚ ɮɨɪɦɢɪɭɟɬɫɹ ɧɨɜɚɹ ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ.

ɋɬɚɬɢɱɟɫɤɚɹ ɚɫɢɦɩɬɨɬɢɱɟɫɤɚɹ ɝɨɪɨɞɫɤɚɹ ɫɬɪɭɤɬɭɪɚ ɛɢɮɭɪɰɢɪɭɟɬ ɤ ɡɚɜɢɫɹɳɟɣ ɨɬ ɜɪɟɦɟɧɢ

ɫɬɪɭɤɬɭɪɟ ɬɢɩɚ ɛɟɝɭɳɟɣ ɜɨɥɧɵ.

Ɍɚɤ ɤɚɤ ɩɚɪɚɦɟɬɪ İ ɞɨɫɬɚɬɨɱɧɨ ɦɚɥ, ɡɚɜɟɪɲɟɧɢɟ ɩɨɥɧɨɝɨ ɰɢɤɥɚ ɜ ɫɢɫɬɟɦɟ ɬɪɟɛɭɟɬ

ɡɧɚɱɢɬɟɥɶɧɨɝɨ ɜɪɟɦɟɧɢ.

8.7 ɇɟɭɫɬɨɣɱɢɜɨɫɬɢ ɢ

ɝɪɚɞɨɨɛɪɚɡɨɜɚɧɢɟ

ȼ ɷɬɨɣ ɝɥɚɜɟ ɦɵ ɪɚɫɫɦɚɬɪɢɜɚɟɦ ɪɚɡɧɨɨɛɪɚɡɧɵɟ ɦɨɞɟɥɢ ɝɨɪɨɞɚ ɜ ɪɚɦɤɚɯ ɩɪɢɛɥɢɠɟɧɢɹ

ɞɢɧɚɦɢɱɟɫɤɨɝɨ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨɝɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ. Ɍɚɤ ɠɟ, ɤɚɤ ɢ ɜ ɩɪɟɞɵɞɭɳɢɯ ɝɥɚɜɚɯ, ɧɚɫ

ɢɧɬɟɪɟɫɭɟɬ ɧɟɭɫɬɨɣɱɢɜɚɹ ɷɜɨɥɸɰɢɹ ɝɨɪɨɞɚ. Ɋɚɡɨɛɪɚɧɧɵɟ ɧɚɦɢ ɩɪɢɦɟɪɵ ɩɨɤɚɡɵɜɚɸɬ, ɱɬɨ

ɧɟɭɫɬɨɣɱɢɜɨɫɬɶ ɹɜɥɹɟɬɫɹ ɢɫɬɨɱɧɢɤɨɦ ɫɥɨɠɧɨɣ ɷɜɨɥɸɰɢɢ. Ɉɫɧɨɜɧɨɣ ɭɩɨɪ ɜ ɷɬɨɣ ɝɥɚɜɟ ɛɵɥ

ɫɞɟɥɚɧ ɧɚ ɯɚɪɚɤɬɟɪ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ ɢ ɟɟ ɢɡɦɟɧɟɧɢɣ. Ȼɵɥɨ

ɩɨɤɚɡɚɧɨ, ɱɬɨ ɜɫɥɟɞɫɬɜɢɟ

ɦɚɥɵɯ ɢɡɦɟɧɟɧɢɣ ɜɧɟɲɧɟɣ ɫɪɟɞɵ ɨɬ ɨɞɧɨɪɨɞɧɨɣ, ɧɟ ɡɚɜɢɫɹɳɟɣ ɨɬ ɜɪɟɦɟɧɢ ɝɨɪɨɞɫɤɨɣ

ɫɬɪɭɤɬɭɪɵ ɦɨɝɭɬ ɛɢɮɭɪɰɢɪɨɜɚɬɶ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɨ ɭɩɨɪɹɞɨɱɟɧɧɵɟ, ɡɚɜɢɫɹɳɢɟ ɨɬ ɜɪɟɦɟɧɢ

ɝɟɬɟɪɨɝɟɧɧɵɟ ɫɬɪɭɤɬɭɪɵ.

ɂɡ ɩɪɢɦɟɪɨɜ, ɩɪɢɜɟɞɟɧɧɵɯ ɡɞɟɫɶ, ɦɵ ɜɢɞɢɦ, ɤɚɤɭɸ ɜɚɠɧɭɸ ɪɨɥɶ ɜ ɩɪɨɰɟɫɫɟ

ɮɨɪɦɢɪɨɜɚɧɢɹ ɝɨɪɨɞɫɤɨɣ ɫɬɪɭɤɬɭɪɵ ɢɝɪɚɟɬ ɮɚɤɬɨɪ ɞɢɮɮɭɡɢɢ: ɧɟɭɫɬɨɣɱɢɜɚɹ ɦɨɞɟɥɶ ɝɨɪɨɞɚ

ɦɨɠɟɬ ɛɵɬɶ ɫɬɚɛɢɥɢɡɢɪɨɜɚɧɚ ɜɜɟɞɟɧɢɟɦ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɵɯ ɩɟɪɟɦɟɧɧɵɯ.

Ʉɨɧɟɱɧɨ, ɦɨɠɧɨ

ɧɚɣɬɢ ɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɵɟ ɩɪɢɦɟɪɵ. Ɏɚɤɬɢɱɟɫɤɢ ɜɥɢɹɧɢɟ ɪɚɡɦɟɪɨɜ ɢ ɮɚɤɬɨɪɚ ɞɢɮɮɭɡɢɢ ɧɚ

ɷɜɨɥɸɰɢɸ ɝɨɪɨɞɚ ɟɳɟ ɦɚɥɨ ɢɡɭɱɟɧɨ. ɉɪɟɞɫɬɚɜɥɹɟɬɫɹ, ɱɬɨ ɦɚɥɵɟ ɝɨɪɨɞɫɤɢɟ ɚɪɟɚɥɵ ɢɦɟɸɬ

ɬɟɧɞɟɧɰɢɸ ɤ ɨɞɧɨɪɨɞɧɨɫɬɢ, ɬɨɝɞɚ ɤɚɤ ɛɨɥɶɲɢɟ — ɤ ɝɟɬɟɪɨɝɟɧɧɨɫɬɢ. ɉɨɫɤɨɥɶɤɭ ɩɪɨɰɟɫɫ

ɪɚɫɲɢɪɟɧɢɹ ɝɨɪɨɞɚ ɨɛɵɱɧɨ ɬɟɱɟɬ ɨɱɟɧɶ ɦɟɞɥɟɧɧɨ, ɦɵ ɦɨɠɟɦ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɪɚɡɦɟɪ ɝɨɪɨɞɚ

ɤɚɤ ɛɢɮɭɪɤɚɰɢɨɧɧɵɣ ɩɚɪɚɦɟɬɪ. ɉɪɢ ɩɟɪɟɯɨɞɟ ɷɬɨɝɨ

ɩɚɪɚɦɟɬɪɚ ɱɟɪɟɡ ɧɟɤɨɬɨɪɵɟ ɤɪɢɬɢɱɟɫɤɢɟ

ɡɧɚɱɟɧɢɹ ɦɨɝɭɬ ɪɚɡɜɢɬɶɫɹ ɛɨɥɟɟ ɫɥɨɠɧɵɟ ɝɨɪɨɞɫɤɢɟ ɫɬɪɭɤɬɭɪɵ. ɗɬɨ

ɢɧɬɭɢɬɢɜɧɨɟ ɩɪɟɞɩɨɥɨɠɟɧɢɟ ɩɪɢɜɨɞɢɬ ɤ ɢɧɨɦɭ ɨɛɴɹɫɧɟɧɢɸ ɪɚɡɧɨɨɛɪɚɡɢɹ ɢ ɫɥɨɠɧɨɫɬɢ

ɷɜɨɥɸɰɢɨɧɧɵɯ ɩɪɨɰɟɫɫɨɜ ɜ ɝɨɪɨɞɚɯ. Ɉɞɧɚɤɨ, ɱɬɨɛɵ ɯɨɪɨɲɨ ɩɨɧɹɬɶ ɩɨɞɨɛɧɵɟ ɩɪɨɰɟɫɫɵ,

ɧɟɨɛɯɨɞɢɦɨ ɩɨɫɬɪɨɢɬɶ ɛɨɥɟɟ ɫɥɨɠɧɵɟ ɦɨɞɟɥɢ ɝɨɪɨɞɨɜ ɢ ɪɚɡɪɚɛɨɬɚɬɶ ɛɨɥɟɟ ɦɨɳɧɵɟ ɚɧɚɥɢ-

ɬɢɱɟɫɤɢɟ ɦɟɬɨɞɵ ɢɫɫɥɟɞɨɜɚɧɢɹ.

ɉɪɢɥɨɠɟɧɢɟ: ɋɬɪɭɤɬɭɪɧɵɟ ɢɡɦɟɧɟɧɢɹ ɜ

ɞɜɭɯɤɨɦɩɨɧɟɧɬɧɨɣ ɦɨɞɟɥɢ

ȼ ɷɬɨɦ ɩɪɢɥɨɠɟɧɢɢ ɦɵ ɩɪɢɜɟɞɟɦ ɞɜɚ ɩɪɢɦɟɪɚ ɦɨɞɟɥɟɣ ɮɨɪɦɢɪɨɜɚɧɢɹ ɫɬɪɭɤɬɭɪ. Ɇɵ

ɩɨɤɚɠɟɦ, ɤɚɤ ɩɪɢɦɟɧɹɸɬɫɹ ɪɚɡɥɢɱɧɵɟ ɚɧɚɥɢɬɢɱɟɫɤɢɟ ɦɟɬɨɞɵ ɤ ɢɫɫɥɟɞɨɜɚɧɢɸ ɩɨɜɟɞɟɧɢɹ

ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɣ ɜ ɱɚɫɬɧɵɯ ɩɪɨɢɡɜɨɞɧɵɯ. ȼɚɠɧɵɦ ɩɪɢɦɟɪɨɦ ɞɥɹ ɨɛɴɹɫɧɟɧɢɹ ɤɨɧɰɟɩɰɢɢ

ɡɚɪɨɠɞɟɧɢɹ ɩɨɪɹɞɤɚ ɢɡ ɯɚɨɫɚ ɫɥɭɠɢɬ ɜ ɫɢɧɟɪɝɟɬɢɤɟ ɦɨɞɟɥɶ ɦɨɪɮɨɝɟɧɟɡɚ (ɫɦ. ɏɚɤɟɧ, 1977). ȼ

ɤɚɱɟɫɬɜɟ ɠɟ ɩɪɢɦɟɪɚ, ɢɥɥɸɫɬɪɢɪɭɸɳɟɝɨ ɩɪɨɰɟɫɫ ɫɚɦɨɨɪɝɚɧɢɡɚɰɢɢ ɜ ɞɢɫɫɢɩɚɬɢɜɧɨɣ ɫɢɫɬɟɦɟ

ɯɨɪɨɲɨ ɢɡɜɟɫɬɧɚ ɦɨɞɟɥɶ ɛɪɸɫɫɟɥɹɬɨɪɚ.

8.7.1 Ɇɨɞɟɥɶ ɦɨɪɮɨɝɟɧɟɡɚ

ɉɪɟɤɪɚɫɧɨɣ ɦɨɞɟɥɶɸ ɦɨɪɮɨɝɟɧɟɡɚ ɹɜɥɹɟɬɫɹ ɝɢɞɪɚ — ɠɢɜɨɟ ɫɭɳɟɫɬɜɨ ɞɥɢɧɨɣ ɜ ɧɟɫɤɨɥɶɤɨ

ɦɢɥɥɢɦɟɬɪɨɜ, ɫɨɫɬɨɹɳɟɟ ɢɡ ~ 10

ɤɥɟɬɨɤ ɩɪɢɦɟɪɧɨ 15 ɬɢɩɨɜ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɩɪɨɰɟɫɫ

ɦɨɪɮɨɝɟɧɟɡɚ ɦɨɠɟɬ ɜɵɡɵɜɚɬɶɫɹ ɭɱɚɫɬɢɟɦ ɜ ɛɢɨɯɢɦɢɱɟɫɤɢɯ ɩɪɨɰɟɫɫɚɯ ɩɨ ɤɪɚɣɧɟɣ

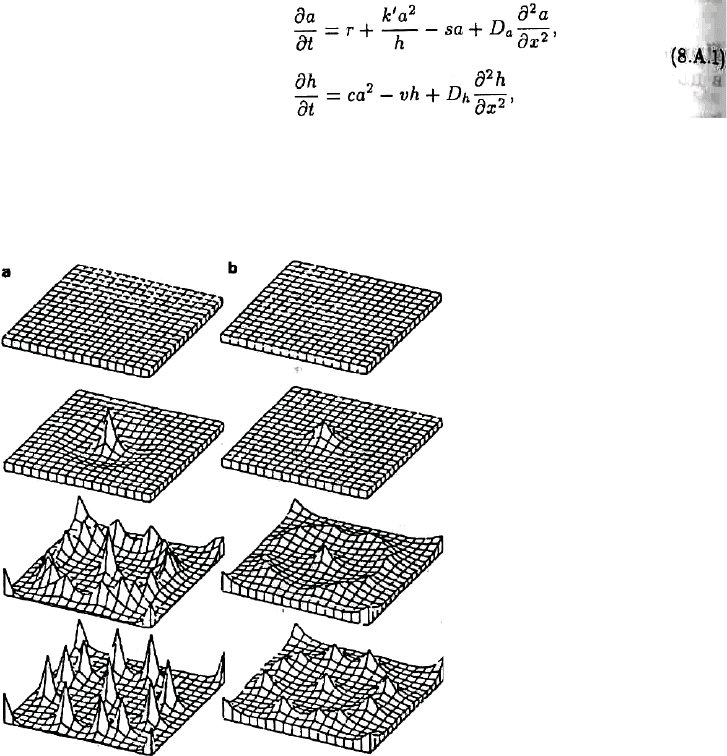
ɦɟɪɟ ɞɜɭɯ ɬɢɩɨɜ ɯɢɦɢɱɟɫɤɢɯ ɜɟɳɟɫɬɜ: ɚɤɬɢɜɚɬɨɪɚ ɢ ɢɧɝɢɛɢɬɨɪɚ. Ɉɛɨɡɧɚɱɢɦ ɤɨɧɰɟɧɬɪɚɰɢɸ

ɚɤɬɢɜɚɬɨɪɚ ɛɭɤɜɨɣ ɚ, ɚ ɢɧɝɢɛɢɬɨɪɚ — ɛɭɤɜɨɣ h. Ɇɨɞɟɥɶ ɡɚɩɢɫɵɜɚɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:

ɝɞɟ r, k', s, ɫ, v, D

ɢ D

, — ɤɨɧɫɬɚɧɬɵ, x — ɞɢɫɬɚɧɰɢɨɧɧɵɣ ɩɚɪɚɦɟɬɪ. ɇɚ ɪɢɫ. 8.13 ɢ 8.14

ɩɨɤɚɡɚɧɵ ɧɟɤɨɬɨɪɵɟ ɪɟɡɭɥɶɬɚɬɵ ɱɢɫɥɟɧɧɨɝɨ ɪɟɲɟɧɢɹ ɷɬɨɣ ɫɢɫɬɟɦɵ (ɫɦ. ɏɚɤɟɧ, 1977).

ɉɨɫɤɨɥɶɤɭ ɧɚɫ ɧɟ ɢɧɬɟɪɟɫɭɸɬ ɤɨɧɤɪɟɬɧɵɟ ɡɧɚɱɟɧɢɹ ɩɚɪɚɦɟɬɪɨɜ, ɩɪɨɫɬɨ ɨɩɢɲɟɦ ɧɟɤɨɬɨɪɵɟ

ɜɨɡɦɨɠɧɵɟ ɫɬɪɭɤɬɭɪɵ.

Ɋɢɫ. 8.14. Ⱦɜɭɦɟɪɧɚɹ ɦɨɞɟɥɶ ɦɨɪɮɨɝɟɧɟɡɚ: ɚ) ɤɨɧɰɟɧɬɪɚɰɢɹ ɚɤɬɢɜɚɬɨɪ»! b) ɤɨɧɰɟɧɬɪɚɰɢɹ

ɢɧɝɢɛɢɬɨɪɚ.

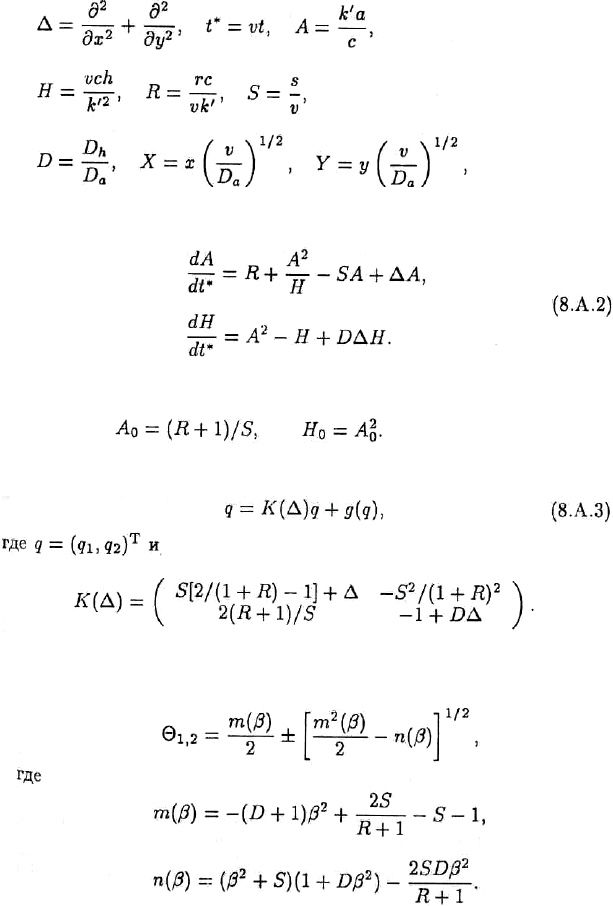
ȼɜɟɞɹ ɨɛɨɡɧɚɱɟɧɢɹ

ɦɵ ɦɨɠɟɦ ɩɟɪɟɩɢɫɚɬɶ (8.Ⱥ.1) ɤɚɤ

ɋɬɚɰɢɨɧɚɪɧɨɟ ɨɞɧɨɪɨɞɧɨɟ ɪɟɲɟɧɢɟ ɫɢɫɬɟɦɵ (8.Ⱥ.2) ɢɦɟɟɬ ɜɢɞ

ȼɜɟɞɹ ɩɚɪɚɦɟɬɪɵ q

= Ⱥ – A

ɢ q

= Ǿ — ɇ

, ɩɨɥɭɱɢɦ ɧɨɜɭɸ ɮɨɪɦɭ ɫɢɫɬɟɦɵ (8.Ⱥ.2)

Ⱦɥɹ ɥɢɧɟɣɧɨɝɨ ɚɧɚɥɢɡɚ ɭɫɬɨɣɱɢɜɨɫɬɢ ɫɬɚɰɢɨɧɚɪɧɨɝɨ ɪɟɲɟɧɢɹ ɷɬɨɝɨ ɍɪɚɜɧɟɧɢɹ, ɨɩɭɫɬɢɜ g(q)

ɢ ɩɨɞɫɬɚɜɢɜ q = Įȕxȡ(ȓȕ

t), ɝɞɟ Į, ȕ ɢ

[= (X,Ȋ)

] — ɜɟɤɬɨɪɵ, ɦɵ ɩɨɥɭɱɢɦ ɫɥɟɞɭɸɳɢɟ

ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ:

Ʌɟɝɤɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɩɪɢ ɧɟɤɨɬɨɪɵɯ ɡɧɚɱɟɧɢɹɯ ȕ ɢ R ɢɦɟɟɬ ɦɟɫɬɨ ɧɟɭɫɬɨɣɱɢɜɨɫɬɶ. ɉɪɢɦɟɧɹɹ ɤ

ɡɚɞɚɱɟ ɩɪɢɧɰɢɩ ɩɨɞɱɢɧɟɧɢɹ, ɏɚɤɟɧ (1977) ɚɧɚɥɢɬɢɱɟɫɤɢ ɩɨɤɚɡɚɥ, ɱɬɨ ɢɡ ɷɬɨɣ ɧɟɥɢɧɟɣɧɨɣ

ɫɢɫɬɟɦɵ ɦɨɝɭɬ ɡɚɪɨɠɞɚɬɶɫɹ ɨɱɟɧɶ ɫɥɨɠɧɵɟ ɫɬɪɭɤɬɭɪɵ

8.7.2 Ȼɪɸɫɫɟɥɹɬɨɪ

Ⱦɪɭɝɢɦ ɯɨɪɨɲɨ ɢɡɜɟɫɬɧɵɦ ɩɪɢɦɟɪɨɦ ɦɨɞɟɥɢ «ɪɟɚɤɰɢɹ-ɞɢɮɮɭɡɢɹ» ɹɜɥɹɟɬɫɹ ɬɪɢɦɨɥɟɤɭɥɹɪɧɚɹ

ɦɨɞɟɥɶ ɛɪɸɫɫɟɥɹɬɨɪɚ. ɗɬɚ ɦɨɞɟɥɶ ɢɞɟɚɥɶɧɨ ɩɨɞɯɨɞɢɬ ɞɥɹ ɢɡɭɱɟɧɢɹ ɤɨɨɩɟɪɚɬɢɜɧɵɯ ɩɪɨɰɟɫɫɨɜ

ɯɢɦɢɱɟɫɤɨɣ ɤɢɧɟɬɢɤɢ (ɇɢɤɨɥɢɫ ɢ ɉɪɢɝɨɠɢɣ, 1977). ɉɨɫɤɨɥɶɤɭ ɦɚɬɟɦɚɬɢɱɟɫɤɢɣ ɚɧɚɥɢɡ ɷɬɨɣ

ɦɨɞɟɥɢ ɩɪɟɞɩɨɥɚɝɚɟɬ ɧɟɤɨɬɨɪɭɸ ɦɚɬɟɦɚɬɢɱɟɫɤɭɸ ɢɫɤɭɲɟɧɧɨɫɬɶ, ɦɵ ɩɪɢɜɟɞɟɦ ɟɝɨ ɜ ɞɟɬɚɥɹɯ.

ɉɨɫɥɟɞɭɸɳɟɟ ɢɡɥɨɠɟɧɢɟ ɨɫɧɨɜɚɧɨ ɧɚ ɪɚɛɨɬɚɯ ɇɢɤɨɥɢɫɚ ɢ ɉɪɢɝɨɠɢɧɚ (1977) ɢ ɏɚɤɟɧɚ

(1977).

Ɋɚɫɫɦɨɬɪɢɦ ɫɯɟɦɭ

ɪɟɚɤɰɢɣ ɛɪɸɫɫɟɥɹɬɨɪɚ ɦɟɠɞɭ ɦɨɥɟɤɭɥɚɦɢ ɫɥɟɞɭɸɳɢɯ ɬɢɩɨɜ: A, X, Ȋ,

ȼ, D ɢ Ǽ

ɋɨɨɬɜɟɬɫɬɜɭɸɳɢɟ «ɩɪɢɜɟɞɟɧɧɵɟ» ɤɨɧɰɟɧɬɪɚɰɢɢ ɜɟɳɟɫɬɜ Ⱥ, ȼ, X ɢ Y ɨɛɨɡɧɚɱɟɧɵ ɤɚɤ Į, ȕ, x ɢ

ɭ. Ʉɨɧɰɟɧɬɪɚɰɢɢ ɚ ɢ ȕ ɫɱɢɬɚɸɬɫɹ ɡɞɟɫɶ ɩɨɫɬɨɹɧɧɵɦɢ, ɬɨɝɞɚ ɤɚɤ x ɢ ɭ — ɩɟɪɟɦɟɧɧɵɦɢ.

ɋɨɝɥɚɫɧɨ ɇɢɤɨɥɢɫɭ ɢ ɉɪɢɝɨɠɢɧɭ (1977), «ɩɪɢɜɟɞɟɧɧɵɟ» ɩɟɪɟɦɟɧɧɵɟ x ɢ ɭ ɜ ɨɞɧɨɦɟɪɧɨɦ

ɩɪɨɫɬɪɚɧɫɬɜɟ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ r ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɭɪɚɜɧɟɧɢɹɦ

ɝɞɟ Θ

ɢ Θ

— ɞɢɮɮɭɡɢɨɧɧɵɟ ɤɨɧɫɬɚɧɬɵ, ɢ 0 ≤ r < R. Ƚɪɚɧɢɰɚ ɨɛɥɚɫɬɢ ɨɛɨɡɧɚɱɟɧɚ ɤɚɤ D.

ɂɦɟɸɬɫɹ ɞɜɚ ɬɢɩɚ ɝɪɚɧɢɱɧɵɯ ɭɫɥɨɜɢɣ

ȼ ɬɟɪɦɢɧɚɯ Ʉ = ||k

|| = K(0) ɭɫɥɨɜɢɟ ɞɢɮɮɭɡɢɨɧɧɨɣ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ, ɜɟɞɭɳɟɣ ɤ ɩɨɹɜɥɟɧɢɸ

ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɵɯ ɫɬɪɭɤɬɭɪ, ɢɦɟɟɬ ɫɥɟɞɭɸɳɢɣ ɜɢɞ: detK > 0, tr K < 0 ɢ k

< 0 => k

> 0 (ɫɦ.

Ɋɚɡɠɟɜɚɣɤɢɧ ȼ. ɇ., «ɂɫɫɥɟɞɨɜɚɧɢɟ ɩɪɨɫɬɪɚɧɫɬɜɟɧɧɵɯ ɫɬɪɭɤɬɭɪ ɜ ɡɚɞɚɱɚɯ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ

ɷɤɨɥɨɝɢɢ», ɀȼɆ ɢ ɆɎ, 1982, ɬ. 22, ɜɵɩ. 3, ɫ. 611-622). —

ɉɪɹɦ. ɪɟɞ.