Занг В.Б. Синергетическая экономика. Время и перемены в нелинейной экономической теории
Подождите немного. Документ загружается.

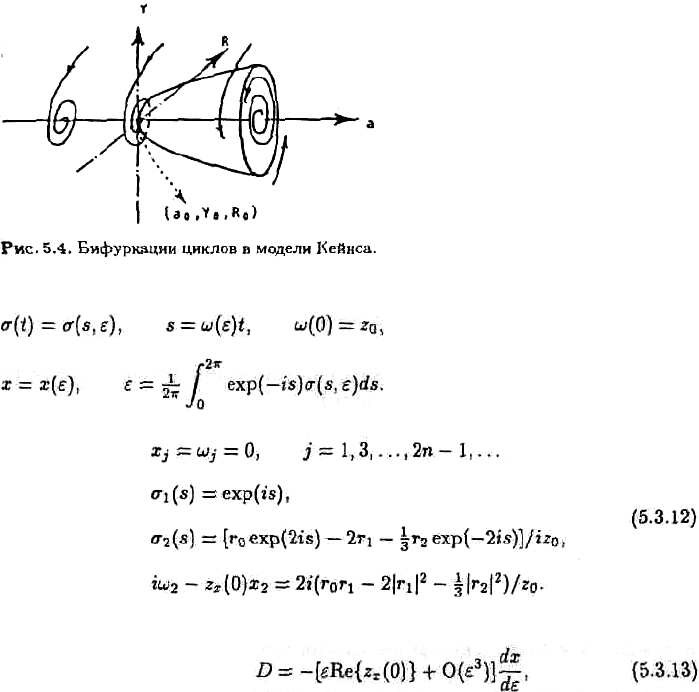
ɝɞɟ
Ʉɨɷɮɮɢɰɢɟɧɬɵ ɞɥɹ ɧɢɡɲɢɯ ɫɬɟɩɟɧɟɣ
ε
ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɫɨɨɬɧɨɲɟɧɢɣ
ɂɡ (5.3.12) ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɬɨɱɧɵɟ ɡɧɚɱɟɧɢɹ ɜɟɥɢɱɢɧ ɯ
j
,
ω
j
(j = l,2,3),
σ
1
ɢ
σ
2
.
Ɉɩɪɟɞɟɥɢɦ D ɤɚɤ
ɝɞɟ ɯ = ɯ
2
ε
2
/2+O(
ε
4
). ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɬɟɨɪɟɦɨɣ ɮɚɤɬɨɪɢɡɚɰɢɢ (ɫɦ. Ƀɨɫɫ ɢ Ⱦɠɨɡɟɮ, 1980,
ɝɥ. VII), ɟɫɥɢ D ɩɨɥɨɠɢɬɟɥɶɧɨ, ɰɢɤɥ ɧɟɭɫɬɨɣɱɢɜ, ɟɫɥɢ ɨɬɪɢɰɚɬɟɥɶɧɨ - ɭɫɬɨɣɱɢɜ. Ɍɚɤɢɦ
ɨɛɪɚɡɨɦ, ɦɵ ɨɩɪɟɞɟɥɢɥɢ ɭɫɥɨɜɢɹ ɭɫɬɨɣɱɢɜɨɫɬɢ ɞɥɹ ɬɟɨɪɟɦɵ 5.3.1.
Ɇɵ ɧɟ ɜɵɩɢɫɚɥɢ ɡɞɟɫɶ ɬɨɱɧɵɯ ɜɵɪɚɠɟɧɢɣ ɞɥɹ r
j
,
ω
j
, x
j
ɢ ɞɪɭɝɢɯ ɩɚɪɚɦɟɬɪɨɜ, ɩɨɫɤɨɥɶɤɭ
ɨɧɢ ɫɥɢɲɤɨɦ ɝɪɨɦɨɡɞɤɢ. Ɋɢɫɭɧɨɤ 5.4 ɢɥɥɸɫɬɪɢɪɭɟɬ ɩɨɜɟɞɟɧɢɟ ɫɢɫɬɟɦɵ. Ɋɚɞɢɭɫ ɰɢɤɥɚ
ɡɚɜɢɫɢɬ ɨɬ ɩɚɪɚɦɟɬɪɚ ɛɢɮɭɪɤɚɰɢɢ: ɩɪɢ ɭɞɚɥɟɧɢɢ ɩɚɪɚɦɟɬɪɚ ɨɬ ɤɪɢɬɢɱɟɫɤɨɝɨ ɡɧɚɱɟɧɢɹ ɪɚɞɢɭɫ
ɪɚɫɬɟɬ.
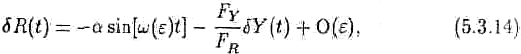
ɉɪɨɰɟɧɬɧɚɹ ɫɬɚɜɤɚ ɥɟɠɢɬ ɬɨ ɧɢɠɟ, ɬɨ ɜɵɲɟ ɬɨɱɤɢ ɪɚɜɧɨɜɟɫɢɹ, ɬ.ɟ. ɯɨɬɹ ɨɧɚ ɢ ɦɨɠɟɬ
ɩɪɢɛɥɢɠɚɬɶɫɹ ɤ ɡɧɚɱɟɧɢɸ R
0
, ɧɨ ɧɟ ɦɨɠɟɬ ɩɨɫɬɨɹɧɧɨ ɨɫɬɚɜɚɬɶɫɹ ɟɦɭ ɪɚɜɧɨɣ. ɉɪɢɛɥɢɡɢɜɲɢɫɶ
ɤ ɪɚɜɧɨɜɟɫɢɸ, ɨɧɚ ɫɬɪɟɦɢɬɫɹ ɨɬ ɧɟɝɨ ɩɪɨɱɶ. ȿɟ ɩɨɛɭɠɞɚɟɬ ɤ ɷɬɨɦɭ ɧɟɥɢɧɟɣɧɵɣ ɯɚɪɚɤɬɟɪ
ɜɡɚɢɦɨɞɟɣɫɬɜɢɹ ɩɪɨɰɟɧɬɧɨɣ ɫɬɚɜɤɢ ɢ ɨɛɴɟɦɚ ɩɪɨɢɡɜɨɞɫɬɜɚ. Ⱥɧɚɥɨɝɢɱɧɨ ɦɨɠɧɨ ɨɛɴɹɫɧɢɬɶ
ɩɨɜɟɞɟɧɢɟ ɧɚɰɢɨɧɚɥɶɧɨɝɨ ɞɨɯɨɞɚ ɍ.
ɂɡ (5.3.3) ɢɦɟɟɦ
ɝɞɟ δR(t) = {R(t) - R
0
}/2
ε
, δY(t) = {Y(t) – Y
0
}/2
ε
. Ɍɚɤ ɤɚɤ δY(t) — ɩɟɪɢɨɞɢɱɟɫɤɚɹ ɮɭɧɤɰɢɹ,
ɤɨɬɨɪɚɹ «ɧɟ ɡɚɜɢɫɢɬ» ɨɬ δR(t), ɜɢɞɢɦ, ɱɬɨ ɜɡɚɢɦɨɞɟɣɫɬɜɢɟ ɦɟɠɞɭ ɞɜɭɦɹ ɩɟɪɟɦɟɧɧɵɦɢ ɦɨɠɟɬ
ɛɵɬɶ ɜɟɫɶɦɚ ɫɥɨɠɧɵɦ.
5.4 ɏɚɪɚɤɬɟɪ ɧɟɪɚɜɧɨɜɟɫɧɨɫɬɢ ɜ ɦɨɞɟɥɢ
ɛɟɡ ɪɚɜɧɨɜɟɫɢɣ
ȼ ɷɬɨɦ ɪɚɡɞɟɥɟ ɦɵ ɞɚɞɢɦ ɩɪɢɥɨɠɟɧɢɟ ɬɟɨɪɟɦɵ ɏɨɩɮɚ ɨ ɛɢɮɭɪɤɚɰɢɹɯ ɤ ɦɨɞɟɥɢ
ɭɩɪɚɜɥɟɧɢɹ ɡɚɩɚɫɚɦɢ, ɪɚɡɜɢɬɨɣ ɜ ɪɚɦɤɚɯ ɦɚɤɪɨɷɤɨɧɨɦɢɤɢ, ɧɟ ɨɛɥɚɞɚɸɳɟɣ ɪɚɜɧɨɜɟɫɢɟɦ. ɗɬɚ
ɦɨɞɟɥɶ ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɛɵɥɚ ɩɪɟɞɥɨɠɟɧɚ ɜ ɪɚɛɨɬɟ ɗɤɚɥɶɛɚɪɚ (1985). Ɂɚɧɝ (1989f) ɭɬɨɱɧɢɥ ɟɟ
ɜɜɟɞɟɧɢɟɦ ɧɟɥɢɧɟɣɧɨɣ ɮɭɧɤɰɢɢ ɪɟɝɭɥɢɪɨɜɚɧɢɹ ɩɪɨɢɡɜɨɞɫɬɜɚ. Ⱦɚɥɶɧɟɣɲɟɟ ɢɡɥɨɠɟɧɢɟ
ɨɫɧɨɜɵɜɚɟɬɫɹ ɧɚ ɪɟɡɭɥɶɬɚɬɚɯ Ɂɚɧɝɚ.
ɉɭɫɬɶ ɷɤɨɧɨɦɢɤɚ ɫɨɫɬɨɢɬ ɢɡ ɞɜɭɯ ɫɟɤɬɨɪɨɜ — ɞɨɦɨɯɨɡɹɣɫɬɜ ɢ
ɮɢɪɦ, ɢ ɬɪɟɯ ɜɢɞɨɜ ɬɨɜɚɪɚ:
ɞɟɧɟɝ, ɬɪɭɞɚ ɢ ɩɪɨɞɭɤɬɨɜ ɩɪɨɢɡɜɨɞɫɬɜɚ. ɉɪɨɞɭɤɬɵ ɩɪɨɢɡɜɨɞɫɬɜɚ ɦɨɝɭɬ ɧɚɤɚɩɥɢɜɚɬɶɫɹ
ɮɢɪɦɚɦɢ, ɧɨ ɧɟ ɞɨɦɨɯɨɡɹɟɜɚɦɢ. Ɏɢɪɦɵ ɢɦɟɸɬ ɩɪɟɞɜɚɪɢɬɟɥɶɧɵɟ ɨɠɢɞɚɧɢɹ (ɨɰɟɧɤɢ) ɫɩɪɨɫɚ
ɩɪɨɞɭɤɰɢɢ ɢ ɡɚɝɪɭɠɚɸɬ ɩɪɨɢɡɜɨɞɫɬɜɨ ɫ ɭɱɟɬɨɦ ɨɠɢɞɚɟɦɨɝɨ ɫɛɵɬɚ, ɩɨɞɞɟɪɠɢɜɚɹ ɡɚɞɚɧɧɨɟ
ɨɬɧɨɲɟɧɢɟ ɦɟɠɞɭ ɫɛɵɜɚɟɦɵɦ ɢ ɢɦɟɸɳɢɦɫɹ ɜ ɧɚɥɢɱɢɢ (ɧɚɤɨɩɥɟɧɧɵɦ) ɬɨɜɚɪɨɦ.
ɉɪɨɢɡɜɨɞɫɬɜɨ ɩɨɧɭɠɞɚɟɬɫɹ ɤ ɮɭɧɤɰɢɨɧɢɪɨɜɚɧɢɸ ɫɜɨɢɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɦɨɳɧɨɫɬɹɦɢ.
ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɞɨɦɨɯɨɡɹɟɜɚ ɢ ɮɢɪɦɵ ɜɫɬɪɟɱɚɸɬɫɹ ɧɚ ɪɵɧɤɟ ɬɪɭɞɚ. Ɍɟɤɭɳɚɹ
ɜɟɥɢɱɢɧɚ ɨɛɦɟɧɚ ɧɚ ɪɵɧɤɟ ɬɪɭɞɚ ɡɚɞɚɟɬɫɹ ɮɨɪɦɭɥɨɣ L = min(L*, L
d
), ɝɞɟ L* —
ɮɢɤɫɢɪɨɜɚɧɧɵɣ ɨɛɴɟɦ ɬɪɭɞɚ, ɩɪɟɞɥɚɝɚɟɦɨɝɨ ɞɨɦɨɯɨɡɹɟɜɚɦɢ ɤ ɩɪɨɞɚɠɟ, L
d
— ɨɛɴɟɦ ɬɪɭɞɚ,
ɤɨɬɨɪɵɣ ɮɢɪɦɵ ɩɵɬɚɸɬɫɹ ɤɭɩɢɬɶ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ L
d
= L
d
(V, S
E
), ɝɞɟ V — ɨɛɴɟɦ ɡɚɩɚɫɚ
ɬɨɜɚɪɨɜ, S
E
— ɨɛɴɟɦ ɨɠɢɞɚɟɦɨɝɨ ɫɛɵɬɚ. ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɜ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɟɞɢɧɢɰɚɯ
ɢɡɦɟɪɟɧɢɹ ɬɟɤɭɳɢɣ ɨɛɴɟɦ ɜɵɯɨɞɚ ɩɪɨɞɭɤɰɢɢ ɪɚɜɟɧ dL(d > 0). ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ ɬɚɤɠɟ, ɱɬɨ
ɮɢɪɦɵ ɭɩɪɚɜɥɹɸɬ ɩɪɨɢɡɜɨɞɫɬɜɨɦ ɬɚɤɢɦ ɨɛɪɚɡɨɦ, ɱɬɨ V = f(S
E
), ɝɞɟ f' > 0 ɢ f" ɧɟ ɪɚɜɧɨ ɧɭɥɸ.
ɇɟɪɚɜɟɧɫɬɜɨ f' > 0 ɨɡɧɚɱɚɟɬ, ɱɬɨ ɜɟɥɢɱɢɧɚ ɬɪɟɛɭɟɦɵɯ ɡɚɩɚɫɨɜ (ɧɚɤɨɩɥɟɧɢɣ) ɬɨɜɚɪɚ ɹɜɥɹɟɬɫɹ
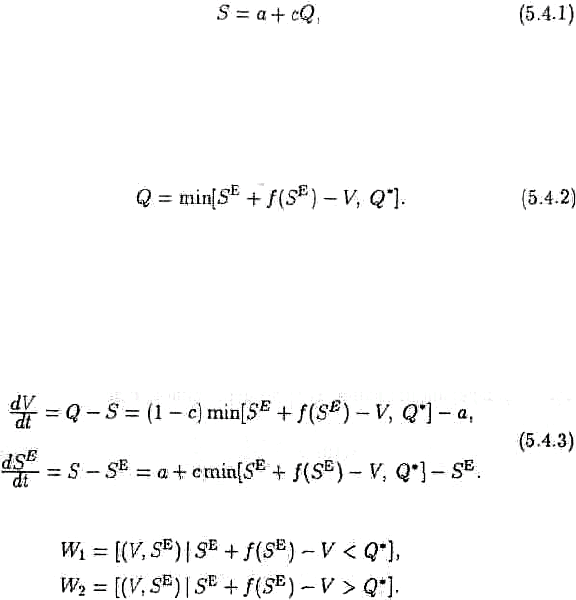
ɜɨɡɪɚɫɬɚɸɳɟɣ ɮɭɧɤɰɢɟɣ S
E
. ɗɬɨ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɥɢɬɟɪɚɬɭɪɧɵɦ ɞɚɧɧɵɦ ɩɨ
ɦɢɤɪɨɧɚɤɨɩɥɟɧɢɹɦ.
ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ ɷɮɮɟɤɬɢɜɧɵɣ ɫɩɪɨɫ ɩɨɬɪɟɛɢɬɟɥɟɣ S ɧɚɩɪɚɜɥɟɧ ɧɚ ɦɚɤɫɢɦɢɡɚɰɢɸ
ɮɭɧɤɰɢɢ ɩɨɥɟɡɧɨɫɬɢ Ʉɨɛɛɚ-Ⱦɭɝɥɚɫɚ U = AS
b
(M/p)
l-b
, ɨɬɪɚɠɚɸɳɟɣ ɫɛɵɬ ɬɪɭɞɚ ɤɚɤ ɬɨɜɚɪɚ ɢ
ɛɸɞɠɟɬɧɵɟ ɨɝɪɚɧɢɱɟɧɢɹ, ɝɞɟ ɪ — ɰɟɧɚ ɬɨɜɚɪɚ, Ɇ/ɪ — ɠɟɥɚɟɦɵɣ ɛɚɥɚɧɫ, Ⱥ (Ⱥ > 0) ɢ b (0 < b <
1) — ɩɚɪɚɦɟɬɪɵ. Ɏɭɧɤɰɢɹ S ɡɚɞɚɟɬɫɹ ɫɨɨɬɧɨɲɟɧɢɟɦ
ɝɞɟ ɚ = bɆ
0
/ɪ, ɫ = wb/pd, w — ɧɨɦɢɧɚɥɶɧɚɹ ɡɚɪɚɛɨɬɧɚɹ ɩɥɚɬɚ, ɚ Ɇ
0
— ɧɢɠɧɢɣ ɭɪɨɜɟɧɶ
ɞɟɧɟɠɧɨɝɨ ɩɨɬɪɟɛɥɟɧɢɹ ɧɚɫɟɥɟɧɢɹ.
Ɏɢɪɦɵ ɩɪɨɢɡɜɨɞɹɬ ɫɬɨɥɶɤɨ ɩɪɨɞɭɤɰɢɢ, ɫɤɨɥɶɤɨ, ɤɚɤ ɢɦ ɤɚɠɟɬɫɹ, ɨɧɢ ɦɨɝɭɬ ɩɪɨɞɚɬɶ, S
E
,
ɩɥɸɫ ɩɨɩɪɚɜɤɭ ɧɚ ɧɚɤɨɩɥɟɧɢɟ f(S
E
) — V. Ɂɧɚɱɢɬ, ɩɨɬɪɟɛɧɨɫɬɶ ɜ ɬɪɭɞɟ ɡɚɞɚɟɬɫɹ ɮɨɪɦɭɥɨɣ L
d
=
[S
E
+ f(S
E
) — V]/d. ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɟɫɥɢ ɧɚ ɪɵɧɤɟ ɬɪɭɞɚ ɢɦɟɟɬɫɹ ɧɟɞɨɫɬɚɬɨɤ, ɨɛɴɟɦ
ɩɪɨɢɡɜɨɞɫɬɜɚ ɧɟ ɦɨɠɟɬ ɩɪɟɜɵɫɢɬɶ ɜɟɥɢɱɢɧɭ Q* = dL*. Ɍɟɤɭɳɢɣ ɜɵɩɭɫɤ ɩɪɨɞɭɤɰɢɢ ɞɨɥɠɟɧ
ɫɨɫɬɚɜɥɹɬɶ
ȼ ɷɬɨɣ ɧɟɪɚɜɧɨɜɟɫɧɨɣ ɦɨɞɟɥɢ ɪɵɧɨɤ ɬɪɭɞɚ ɬɚɤɠɟ ɧɟ ɢɦɟɟɬ ɪɚɜɧɨɜɟɫɢɹ, ɧɨ ɮɢɪɦɵ ɦɨɝɭɬ
ɩɨɞɞɟɪɠɢɜɚɬɶ ɩɪɨɢɡɜɨɞɫɬɜɨ, ɩɨɡɜɨɥɹɸɳɟɟ ɭɞɨɜɥɟɬɜɨɪɹɬɶ ɷɮɮɟɤɬɢɜɧɵɣ ɫɩɪɨɫ ɧɚɫɟɥɟɧɢɹ. ɋ
ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɯɨɬɹ ɪɵɧɨɤ ɬɨɜɚɪɨɜ ɜɫɟɝɞɚ ɧɚɯɨɞɢɬɫɹ ɜ ɪɚɜɧɨɜɟɫɢɢ, ɮɢɪɦɵ ɦɨɝɭɬ
ɫɬɚɥɤɢɜɚɬɶɫɹ ɫ ɧɟɪɚɜɧɨɜɟɫɧɨɣ ɫɢɬɭɚɰɢɟɣ, ɟɫɥɢ ɠɟɥɚɟɦɨɟ ɢ ɪɟɚɥɶɧɨɟ ɧɚɤɨɩɥɟɧɢɹ ɨɤɚɠɭɬɫɹ
ɪɚɡɥɢɱɧɵ.
Ɇɵ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɢɡɦɟɧɟɧɢɟ ɮɭɧɤɰɢɢ V
ɪɚɜɧɨ Q — S, ɢ ɱɬɨ S
E
ɚɞɚɩɬɢɜɧɨ
ɪɟɝɭɥɢɪɭɟɬɫɹ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɪɚɡɧɨɫɬɶɸ S — S
E
. Ⱦɢɧɚɦɢɤɚ ɫɢɫɬɟɦɵ ɨɩɢɫɵɜɚɟɬɫɹ
ɭɪɚɜɧɟɧɢɹɦɢ
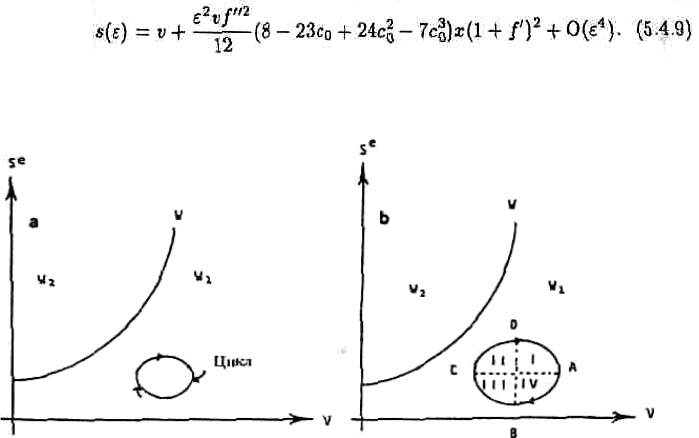
Ʉɪɢɜɚɹ ɩɟɪɟɤɥɸɱɟɧɢɣ ɨɩɪɟɞɟɥɹɟɬɫɹ ɭɪɚɜɧɟɧɢɟɦ S
E
+ f(S
E
) — V = Q*. ɉɥɨɫɤɨɫɬɶ (V, S
E
)
ɪɚɡɞɟɥɟɧɚ ɷɬɨɣ ɤɪɢɜɨɣ ɧɚ ɞɜɟ ɱɚɫɬɢ:
Ʌɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ, ɟɫɥɢ ɬɟɤɭɳɚɹ ɬɪɚɟɤɬɨɪɢɹ ɩɪɢɧɚɞɥɟɠɢɬ ɨɛɥɚɫɬɢ W
2
, ɫɢɫɬɟɦɚ ɥɢɧɟɣɧɚ.
ɗɬɨɬ ɫɥɭɱɚɣ ɞɟɬɚɥɶɧɨ ɢɡɭɱɟɧ ɗɤɚɥɶɛɚɪɨɦ (1985).
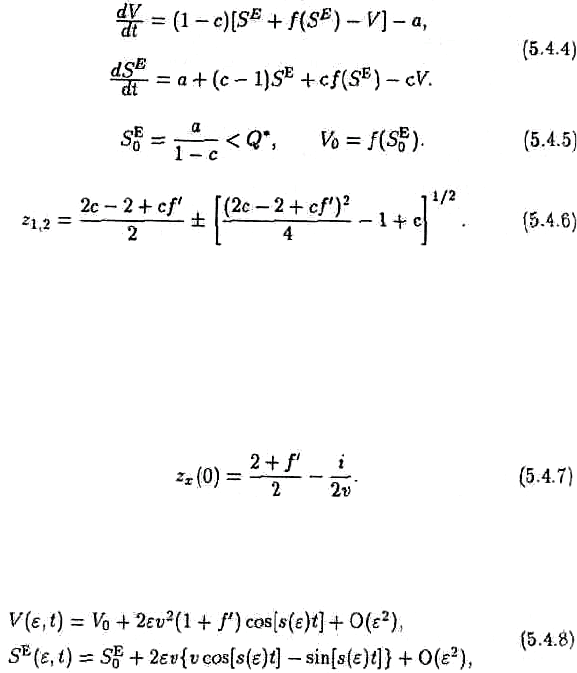
Ɇɵ ɨɫɬɚɧɨɜɢɦɫɹ ɬɨɥɶɤɨ ɧɚ ɫɥɭɱɚɟ (V, S
E
) ∈ W
1
. ɂɦɟɧɧɨ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɧɚ ɪɵɧɤɟ ɬɪɭɞɚ
ɜɨɡɦɨɠɧɚ ɛɟɡɪɚɛɨɬɢɰɚ. Ⱦɢɧɚɦɢɤɚ ɫɢɫɬɟɦɵ ɨɩɢɫɵɜɚɟɬɫɹ ɭɪɚɜɧɟɧɢɹɦɢ
ȿɞɢɧɫɬɜɟɧɧɚɹ ɬɨɱɤɚ ɪɚɜɧɨɜɟɫɢɹ ɡɚɞɚɟɬɫɹ ɫɨɨɬɧɨɲɟɧɢɹɦɢ
ɋɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ z
i
ɪɚɜɧɵ
ɉɭɫɬɶ c
0
ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɫɥɨɜɢɸ 2ɫ — 2 + ɫf' = 0. Ɍɚɤ ɤɚɤ ɫ
0
= 2/(2+f') ɢ f' > 0, ɢɦɟɟɬ ɦɟɫɬɨ
ɧɟɪɚɜɟɧɫɬɜɨ 0 < c
0
< 1. ɉɨɫɤɨɥɶɤɭ ɫ = wb/pd, ɝɞɟ 0 < b < 1, ɭɫɥɨɜɢɟ 0 < c
0
< 1 ɜɵɬɟɤɚɟɬ ɢɡ ɬɨɝɨ,
ɱɬɨ pd > 0. Ɉɞɧɚɤɨ ɢɡ Q = dL ɦɵ ɜɢɞɢɦ, ɱɬɨ w < pd ɨɡɧɚɱɚɟɬ, ɱɬɨ ɩɪɢɛɵɥɶ ɮɢɪɦɵ ɛɭɞɟɬ
ɩɨɥɨɠɢɬɟɥɶɧɨɣ. Ɇɨɠɧɨ ɧɚɣɬɢ ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɟ ɡɧɚɱɟɧɢɟ c
0
ɮɭɧɤɰɢɢ ɫ. ɉɪɢ ɫ = c
0
ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɪɚɜɧɵ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ iv ɢ —iv, ɝɞɟ v = (1 — c
0
)
1
/
2
. Ȼɭɞɟɦ
ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɫ ɤɚɤ ɛɢɮɭɪɤɚɰɢɨɧɧɵɣ ɩɚɪɚɦɟɬɪ, ɢɦɟɸɳɢɣ ɤɪɢɬɢɱɟɫɤɨɟ ɡɧɚɱɟɧɢɟ c
0
. Ɍɚɤ ɤɚɤ ɫ
= wb/pd, ɥɸɛɨɟ ɢɡɦɟɧɟɧɢɟ ɜɟɥɢɱɢɧ w, b, ɪ ɢɥɢ d ɩɪɢɜɨɞɢɬ ɤ ɫɞɜɢɝɭ ɩɚɪɚɦɟɬɪɚ ɫ. ɉɭɫɬɶ ɯ = ɫ
— c
0
. Ɍɨ ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ, ɤɨɬɨɪɨɟ ɩɪɢ ɯ = 0 ɪɚɜɧɨ iv, ɨɛɨɡɧɚɱɢɦ ɱɟɪɟɡ z(ɯ).
Ⱦɢɮɮɟɪɟɧɰɢɪɨɜɚɧɢɟ z(x) ɩɨ ɩɟɪɟɦɟɧɧɨɣ ɯ ɞɚɟɬ
ɂɡ (5.4.7) ɜɢɞɧɨ, ɱɬɨ ɞɟɣɫɬɜɢɬɟɥɶɧɚɹ ɱɚɫɬɶ z
x
(0) ɩɨɥɨɠɢɬɟɥɶɧɚ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɩɨɬɟɪɹ
ɭɫɬɨɣɱɢɜɨɫɬɢ ɭɫɬɚɧɨɜɥɟɧɚ. ɉɪɢ ɯ = 0 ɜɵɩɨɥɧɹɟɬɫɹ ɛɢɮɭɪɤɚɰɢɨɧɧɚɹ ɬɟɨɪɟɦɚ ɏɨɩɮɚ.
Ɍɟɨɪɟɦɚ 5.4.1. ȼ ɨɤɪɟɫɬɧɨɫɬɢ ɪɚɜɧɨɜɟɫɢɹ ɞɥɹ ɦɚɥɵɯ x ɫɭɳɟɫɬɜɭɟɬ ɩɪɟɞɟɥɶɧɵɣ ɰɢɤɥ.
Ȼɢɮɭɪɤɚɰɢɨɧɧɵɣ ɰɢɤɥ ɩɟɪɢɨɞɚ 2π/s(
ε
) ɡɚɞɚɟɬɫɹ ɭɪɚɜɧɟɧɢɹɦɢ
ɝɞɟ
ε
— ɚɦɩɥɢɬɭɞɧɵɣ ɩɚɪɚɦɟɬɪ ɪɚɡɥɨɠɟɧɢɹ ɢ
Ȼɨɥɟɟ ɬɨɝɨ, ɛɢɮɭɪɤɚɰɢɹ ɹɜɥɹɟɬɫɹ ɫɭɩɟɪɤɪɢɬɢɱɟɫɤɨɣ.
ɗɬɚ ɬɟɨɪɟɦɚ ɞɨɤɚɡɚɧɚ Ɂɚɧɝɨɦ (1988f). ɋɨɨɬɜɟɬɫɬɜɭɸɳɟɟ ɩɟɪɢɨɞɢɱɟɫɤɨɟ ɞɜɢɠɟɧɢɟ
ɢɡɨɛɪɚɠɟɧɨ ɧɚ ɪɢɫ. 5.5.
Ɋɢɫ. 5.5. ɮɥɭɤɬɭɚɰɢɹ ɷɤɨɧɨɦɢɤɢ (ɚ) ɨɬ ɫ
0
ɤ ɫ, (b) ɨɬ c
1
ɤ ɫ
2
.
ȿɫɥɢ ɦɵ ɫɦɨɠɟɦ ɩɨɞɞɟɪɠɢɜɚɬɶ ɩɚɪɚɦɟɬɪ
ε
ɞɨɫɬɚɬɨɱɧɨ ɦɚɥɵɦ, ɦɵ ɜɫɟɝɞɚ ɛɭɞɟɦ ɢɦɟɬɶ
ɰɢɤɥ ɜ ɨɛɥɚɫɬɢ W
1
.
ɑɬɨɛɵ ɩɨɞɪɨɛɧɟɟ ɩɨɹɫɧɢɬɶ ɰɢɤɥɢɱɟɫɤɢɣ ɯɚɪɚɤɬɟɪ ɩɨɜɟɞɟɧɢɹ ɫɢɫɬɟɦɵ, ɪɚɡɞɟɥɢɦ ɰɢɤɥ ɧɚ
ɱɟɬɵɪɟ ɱɚɫɬɢ, ɤɚɤ ɧɚ ɪɢɫ. 5.5b. ɉɭɫɬɶ ɫɢɫɬɟɦɚ ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɧɚɯɨɞɢɥɚɫɶ ɜ ɬɨɱɤɟ D, ɜ ɤɨɬɨɪɨɣ
ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟɧɢɹ ɧɚɤɨɩɥɟɧɢɣ ɪɚɜɧɚ ɧɭɥɸ. ɋ ɷɬɨɝɨ ɦɨɦɟɧɬɚ ɨɠɢɞɚɟɦɵɣ ɨɛɴɟɦ ɫɛɵɬɚ
ɧɚɱɢɧɚɟɬ ɩɚɞɚɬɶ. Ɍɚɤ ɤɚɤ ɨɛɴɟɦ ɩɪɨɢɡɜɨɞɫɬɜɚ ɮɢɪɦ, Q, ɪɚɜɟɧ ɩɨɬɪɟɛɢɬɟɥɶɫɤɨɦɭ ɫɩɪɨɫɭ, S, ɜ
ɬɨ ɜɪɟɦɹ
ɤɚɤ ɩɪɟɞɩɨɥɚɝɚɟɦɵɣ ɨɛɴɟɦ ɫɛɵɬɚ ɩɪɟɜɵɲɚɟɬ ɫɩɪɨɫ, ɩɪɨɢɡɜɨɞɢɬɟɥɢ ɞɨɥɠɧɵ ɩɪɟɞɜɢ-
ɞɟɬɶ ɛɭɞɭɳɟɟ ɫɧɢɠɟɧɢɟ ɫɛɵɬɚ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɩɪɟɞɩɨɥɚɝɚɟɦɵɦ ɜ ɧɚɫɬɨɹɳɟɟ ɜɪɟɦɹ.
ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɜɨɡɧɢɤɧɟɬ ɫɧɢɠɟɧɢɟ ɜɟɥɢɱɢɧɵ S . Ⱦɚɥɟɟ ɫɢɫɬɟɦɚ ɩɨɤɢɞɚɟɬ ɬɨɱɤɭ D, ɚ
ɜɟɥɢɱɢɧɚ S
E
ɩɪɨɞɨɥɠɚɟɬ ɭɦɟɧɶɲɚɬɶɫɹ. Ɉɞɧɚɤɨ, ɩɨɫɤɨɥɶɤɭ Q = S
E
+ f(S
E
) - V, ɭɦɟɧɶɲɟɧɢɟ S
E
ɩɪɢɜɟɞɟɬ ɤ ɫɧɢɠɟɧɢɸ ɜɟɥɢɱɢɧɵ Q. Ɍɚɤ ɤɚɤ ɩɨɬɪɟɛɢɬɟɥɶɫɤɢɣ ɫɩɪɨɫ ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɟɣ
ɨɛɴɟɦɚ ɩɪɨɢɡɜɨɞɫɬɜɚ, ɭɦɟɧɶɲɟɧɢɟ ɨɠɢɞɚɟɦɨɝɨ ɨɛɴɟɦɚ ɫɛɵɬɚ ɧɟɹɜɧɨ ɩɪɢɜɟɞɟɬ ɤ ɫɧɢɠɟɧɢɸ
ɩɨɬɪɟɛɢɬɟɥɶɫɤɨɝɨ ɫɩɪɨɫɚ. ɉɨɫɤɨɥɶɤɭ ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟɧɢɹ ɧɚɤɨɩɥɟɧɢɣ ɪɚɜɧɚ Q — S, ɢ ɨɛɟ
ɜɟɥɢɱɢɧɵ Q ɢ S ɭɦɟɧɶɲɚɸɬɫɹ, ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟɧɢɹ ɧɚɤɨɩɥɟɧɢɣ ɦɨɠɟɬ ɨɤɚɡɚɬɶɫɹ ɢ
ɩɨɥɨɠɢɬɟɥɶɧɨɣ, ɢ ɨɬɪɢɰɚɬɟɥɶɧɨɣ. ȼɡɚɢɦɨɞɟɣɫɬɜɢɟ ɷɬɢɯ ɫɢɥ ɩɪɢɜɨɞɢɬ ɤ ɞɜɢɠɟɧɢɸ ɫɢɫɬɟɦɵ
ɩɨ ɧɚɩɪɚɜɥɟɧɢɸ ɤ ɬɨɱɤɟ Ⱥ.
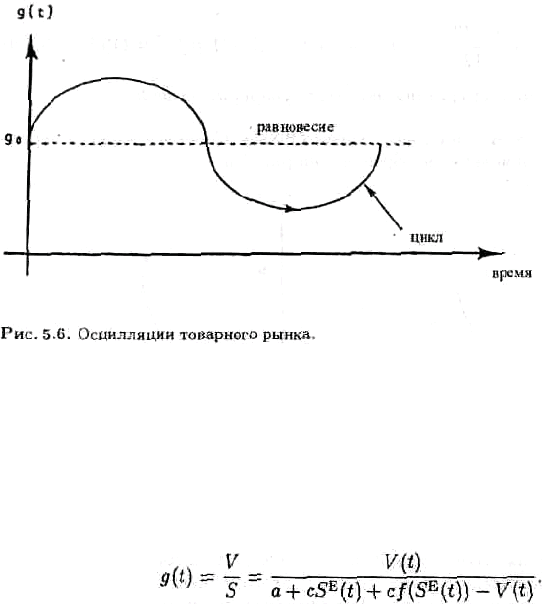
ȼ ɬɨɱɤɟ Ⱥ ɫɢɫɬɟɦɚ ɧɟ ɦɨɠɟɬ ɨɫɬɚɧɨɜɢɬɶɫɹ, ɩɨɬɨɦɭ ɱɬɨ ɨɛɴɟɦ ɩɪɨɢɡɜɨɞɫɬɜɚ ɫɬɚɧɨɜɢɬɫɹ
ɧɢɠɟ ɫɩɪɨɫɚ. Ɉɫɬɚɥɶɧɵɟ ɭɱɚɫɬɤɢ ɞɜɢɠɟɧɢɹ ɩɨ ɰɢɤɥɢɱɟɫɤɨɣ ɬɪɚɟɤɬɨɪɢɢ ɦɨɝɭɬ ɛɵɬɶ
ɨɛɴɹɫɧɟɧɵ ɩɨɞɨɛɧɵɦ ɠɟ ɨɛɪɚɡɨɦ. Ⱦɜɢɠɟɧɢɟ ɛɭɞɟɬ ɩɨɜɬɨɪɹɬɶɫɹ ɞɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɧɟ
ɜɨɡɧɢɤɧɭɬ ɫɥɟɞɭɸɳɢɟ ɛɢɮɭɪɤɚɰɢɢ.
ɉɨɫɤɨɥɶɤɭ ɨɞɧɢɦ ɢɡ ɞɨɫɬɨɢɧɫɬɜ ɷɬɨɣ ɦɨɞɟɥɢ ɹɜɥɹɟɬɫɹ ɨɛɴɹɫɧɟɧɢɟ ɧɚɛɥɸɞɚɟɦɨɝɨ ɜ
ɪɟɚɥɶɧɨɫɬɢ ɰɢɤɥɢɱɟɫɤɨɝɨ ɩɨɜɟɞɟɧɢɹ
ɨɬɧɨɲɟɧɢɹ ɧɚɤɨɩɥɟɧɢɹ ɢ ɫɛɵɬɚ, ɫɥɟɞɭɟɬ ɧɟ ɬɨɥɶɤɨ
ɭɤɚɡɚɬɶ ɧɚ ɮɚɤɬ ɰɢɤɥɢɱɧɨɫɬɢ, ɧɨ ɢ ɢɡɭɱɢɬɶ ɟɝɨ ɯɚɪɚɤɬɟɪ. ȼ ɨɛɥɚɫɬɢ W
1
ɬɟɤɭɳɟɟ ɡɧɚɱɟɧɢɟ
ɧɨɪɦɵ ɬɨɜɚɪɨɨɛɦɟɧɚ ɞɚɟɬɫɹ ɮɨɪɦɭɥɨɣ
ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɷɬɨɬ ɤɨɷɮɮɢɰɢɟɧɬ ɬɨɠɟ ɩɟɪɢɨɞɢɱɟɧ (ɪɢɫ. 5.6).
5.5 Ɇɨɧɟɬɚɪɧɵɟ ɰɢɤɥɵ ɜ ɨɛɨɛɳɟɧɧɨɣ
ɦɨɞɟɥɢ Ɍɨɛɢɧɚ
ȼ ɪɚɡɞ. 3.3 ɦɵ ɭɠɟ ɝɨɜɨɪɢɥɢ ɨ ɦɨɞɟɥɢ Ɍɨɛɢɧɚ (ɫɦ. ɬɚɤɠɟ Ɍɨɛɢɧ, 1965, 1969). Ɋɚɜɧɨɜɟɫɢɟ
ɷɬɨɣ ɫɢɫɬɟɦɵ ɧɟɭɫɬɨɣɱɢɜɨ. Ɇɵ ɩɟɪɟɫɦɨɬɪɢɦ ɚɧɚɥɢɡ, ɞɚɧɧɵɣ Ɍɨɛɢɧɨɦ. Ɉɛɨɛɳɟɧɧɚɹ ɦɨɞɟɥɶ,
ɩɪɟɞɫɬɚɜɥɟɧɧɚɹ ɜ ɷɬɨɣ ɝɥɚɜɟ, ɩɪɢɧɚɞɥɟɠɢɬ Ɂɚɧɝɭ (1990ɖ). ɏɨɬɹ ɦɨɞɟɥɶ, ɤɨɬɨɪɭɸ ɦɵ ɧɚɡɵɜɚɟɦ
ɡɞɟɫɶ ɨɛɨɛɳɟɧɧɨɣ ɦɨɞɟɥɶɸ Ɍɨɛɢɧɚ, ɩɨɯɨɠɚ ɧɚ ɦɨɞɟɥɶ Ɍɨɛɢɧɚ, ɫɮɨɪɦɭɥɢɪɨɜɚɧɧɭɸ ɜ ɪɚɡɞ.
3.3, ɨɧɢ ɜɟɫɶɦɚ ɪɚɡɧɹɬɫɹ ɜ ɞɢɧɚɦɢɤɟ
ɰɟɧ, ɫɜɨɣɫɬɜɚɯ ɭɫɬɨɣɱɢɜɨɫɬɢ ɢ ɧɟɤɨɬɨɪɵɯ ɞɪɭɝɢɯ
ɚɫɩɟɤɬɚɯ. Ɇɵ ɩɪɟɧɟɛɪɟɠɟɦ ɡɞɟɫɶ ɷɮɮɟɤɬɚɦɢ ɚɦɨɪɬɢɡɚɰɢɢ, ɬ.ɟ. ɜ ɮɨɪɦɭɥɟ (3.3.8) ɛɭɞɟɦ
ɫɱɢɬɚɬɶ d = 0. Ɍɟɦ ɧɟ ɦɟɧɟɟ, ɫɨɨɬɧɨɲɟɧɢɹ (3.3.6) ɢ (3.3.8) ɞɥɹ ɨɛɨɛɳɟɧɧɨɣ ɦɨɞɟɥɢ ɨɫɬɚɸɬɫɹ
ɫɩɪɚɜɟɞɥɢɜɵɦɢ. ȼɫɟ ɩɟɪɟɦɟɧɧɵɟ, ɤɨɬɨɪɵɦɢ ɦɵ ɛɭɞɟɦ ɬɭɬ ɩɨɥɶɡɨɜɚɬɶɫɹ, ɢɦɟɸɬ ɬɨɬ ɠɟ ɫɦɵɫɥ,
ɱɬɨ ɢ ɜ ɪɚɡɞ. 3.3.
ȼ ɨɛɨɛɳɟɧɧɨɣ ɦɨɞɟɥɢ Ɍɨɛɢɧɚ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɢɡɦɟɧɟɧɢɹ ɰɟɧ ɨɬɪɚɠɚɸɬ ɤɚɤ
ɢɡɛɵɬɨɱɧɵɣ ɫɩɪɨɫ (ɢɥɢ
ɢɡɛɵɬɨɱɧɨɟ ɩɪɟɞɥɨɠɟɧɢɟ), ɬɚɤ ɢ ɚɞɚɩɬɢɜɧɵɟ ɨɠɢɞɚɧɢɹ. Ɇɵ
ɩɪɢɧɢɦɚɟɦ ɡɚ ɨɫɧɨɜɭ ɬɨɱɤɭ ɡɪɟɧɢɹ ȼɚɥɶɪɚɫɚ ɨ ɬɨɦ, ɱɬɨ, ɤɨɝɞɚ ɢɦɟɟɬ ɦɟɫɬɨ ɢɡɛɵɬɨɱɧɵɣ ɫɩɪɨɫ,
ɰɟɧɵ ɪɚɫɬɭɬ, ɚ ɤɨɝɞɚ ɢɦɟɟɬ ɦɟɫɬɨ ɢɡɛɵɬɨɱɧɨɟ ɩɪɟɞɥɨɠɟɧɢɟ — ɩɚɞɚɸɬ. ɉɨ ɡɚɤɨɧɭ ȼɚɥɶɪɚɫɚ
ɢɡɛɵɬɨɱɧɵɣ ɫɩɪɨɫ ɧɚ ɬɨɜɚɪɵ ɢ ɭɫɥɭɝɢ ɪɚɜɟɧ ɢɡɛɵɬɨɱɧɨɦɭ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɪɚɜɧɨɜɟɫɧɵɦ
ɩɪɟɞɥɨɠɟɧɢɸ (ɬɨɱɧɟɟ, ɟɝɨ ɩɨɬɨɤɭ) ɪɟɚɥɶɧɵɯ
ɫɪɟɞɫɬɜ. ɇɟ ɩɪɢɧɢɦɚɹ ɜ ɪɚɫɱɟɬ ɢɧɮɥɹɰɢɨɧɧɵɟ
ɨɠɢɞɚɧɢɹ, ɦɵ ɦɨɠɟɦ ɩɪɟɞɩɨɥɨɠɢɬɶ ɫɥɟɞɭɸɳɭɸ ɞɢɧɚɦɢɤɭ
ɝɞɟ α— ɩɨɥɨɠɢɬɟɥɶɧɵɣ ɩɨɫɬɨɹɧɧɵɣ ɩɚɪɚɦɟɬɪ, q ɩɪɟɞɫɬɚɜɥɹɟɬ ɨɠɢɞɚɟɦɭɸ ɫɤɨɪɨɫɬɶ
ɢɧɮɥɹɰɢɢ. ȼ ɫɥɭɱɚɟ ɩɨɥɧɨɣ ɜɡɚɢɦɨɡɚɦɟɧɹɟɦɨɫɬɢ ɞɜɭɯ ɩɨɧɹɬɢɣ — ɤɚɩɢɬɚɥɚ ɢ ɞɟɧɟɝ, ɦɨɠɧɨ
ɫɱɢɬɚɬɶ, ɱɬɨ ɮɭɧɤɰɢɹ J ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɫɥɟɞɭɸɳɢɦ ɭɫɥɨɜɢɹɦ: J
k
= +∞, J
q
= -∞, ɚ ɜ ɫɥɭɱɚɟ
ɧɟɩɨɥɧɨɣ ɢɯ ɬɨɠɞɟɫɬɜɟɧɧɨɫɬɢ — J
k
> 0 ɢ J
q
< 0.
ɉɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ ɨɠɢɞɚɟɦɚɹ ɫɤɨɪɨɫɬɶ ɢɡɦɟɧɟɧɢɹ ɰɟɧ ɦɨɠɟɬ ɨɬɥɢɱɚɬɶɫɹ ɨɬ ɪɟɚɥɶɧɨɣ
ɫɤɨɪɨɫɬɢ ɢɧɮɥɹɰɢɢ. ɗɬɚ ɞɢɧɚɦɢɤɚ ɦɨɠɟɬ ɢɦɟɬɶ ɜɢɞ
ɝɞɟ
β
— ɬɚɤ ɧɚɡɵɜɚɟɦɵɣ «ɤɨɷɮɮɢɰɢɟɧɬ ɨɠɢɞɚɧɢɢ».
Ɂɚɜɟɪɲɢɦ ɩɨɫɬɪɨɟɧɢɟ ɦɨɞɟɥɢ ɡɚɩɢɫɶɸ ɭɪɚɜɧɟɧɢɣ, ɤɨɬɨɪɵɟ ɛɭɞɟɦ ɧɚɡɵɜɚɬɶ ɨɛɨɛɳɟɧɧɨɣ
ɦɨɞɟɥɶɸ Ɍɨɛɢɧɚ
ɝɞɟ ɩɟɪɜɵɟ ɞɜɚ ɭɪɚɜɧɟɧɢɹ ɫɨɨɬɜɟɬɫɬɜɭɸɬ (3.3.6) ɢ (3.3.8) (ɫ ɭɱɟɬɨɦ d = 0).
ɉɨɥɨɠɢɬɟɥɶɧɨɟ ɞɥɢɬɟɥɶɧɨɟ ɪɚɜɧɨɜɟɫɢɟ (k
0
, x
0
, q
0
) ɨɩɪɟɞɟɥɹɟɬɫɹ ɤɚɤ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɣ
ɂɡ (5.5.4) ɢɦɟɟɦ
ɱɬɨ ɨɬɪɚɠɚɟɬ ɨɬɧɸɞɶ ɧɟ ɧɟɣɬɪɚɥɶɧɭɸ ɪɨɥɶ ɞɟɧɟɝ ɞɥɹ ɦɨɞɟɥɢ ɜ ɬɨɦ ɫɦɵɫɥɟ, ɱɬɨ
ɨɬɧɨɲɟɧɢɟ «ɤɚɩɢɬɚɥ/ɬɪɭɞ» ɜ ɦɨɧɟɬɚɪɧɨɣ ɦɨɞɟɥɢ ɦɟɧɶɲɟ, ɱɟɦ ɜ ɧɟɦɨɧɟɬɚɪɧɨɣ. ȿɫɥɢ ɯ
0
= 0,
ɢɦɟɟɦ sf(k
0
)/n = k
0
- ɤɚɤ ɜ ɦɨɞɟɥɢ ɋɨɥɨɭ. ȿɫɥɢ ɯ
0
ɩɨɥɨɠɢɬɟɥɶɧɨ, ɬɨ sf(k
0
)/n > k
0
, ɢɥɢ f(k
0
)/k
0
>
n/s, ɢɡ ɱɟɝɨ ɢ ɫɥɟɞɭɟɬ ɮɚɤɬ ɨɬɫɭɬɫɬɜɢɹ ɧɟɣɬɪɚɥɶɧɨɫɬɢ.
Ɍɚɤ ɤɚɤ ɧɚɫ ɢɧɬɟɪɟɫɭɟɬ ɬɨɥɶɤɨ ɭɫɬɨɣɱɢɜɨɫɬɶ ɪɚɜɧɨɜɟɫɢɹ ɢ ɥɨɤɚɥɶɧɨɟ ɩɨɜɟɞɟɧɢɟ ɫɢɫɬɟɦɵ,
ɜɵɩɢɲɟɦ ɫɢɫɬɟɦɭ ɜɛɥɢɡɢ ɪɚɜɧɨɜɟɫɢɹ ɜ ɥɨɤɚɥɶɧɨɦ ɜɢɞɟ. ȼɜɟɞɟɦ ɩɟɪɟɦɟɧɧɵɟ
ɝɞɟ (k, ɯ, q) ɭɞɨɜɥɟɬɜɨɪɹɟɬ (5.5.3), ɚ ɜɟɤɬɨɪ U = (U
1
, U
2
, U
3
)
T
ɞɨɫɬɚɬɨɱɧɨ ɦɚɥ. ɉɨɞɫɬɚɧɨɜɤɚ
(5.5.5) ɜ (5.5.3) ɩɪɢɜɨɞɢɬ ɤ
ɝɞɟ A — ɹɤɨɛɢɚɧ, ɜɵɱɢɫɥɟɧɧɵɣ ɜ ɬɨɱɤɟ ɪɚɜɧɨɜɟɫɢɹ, a N(U, U) — ɤɜɚɞɪɚɬɢɱɧɵɣ ɱɥɟɧ.
əɜɧɵɣ ɜɢɞ ɤɜɚɞɪɚɬɢɱɧɨɝɨ ɱɥɟɧɚ N(U, U) ɜɵɩɢɫɵɜɚɬɶ ɧɟ ɛɭɞɟɦ, ɩɨɫɤɨɥɶɤɭ ɜ ɞɚɥɶɧɟɣɲɟɦ
ɨɧ ɧɟ ɢɫɩɨɥɶɡɭɟɬɫɹ. ȼɜɟɞɟɦ ɜɟɥɢɱɢɧɵ
(5.5.8)
ɋɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɹɤɨɛɢɚɧɚ Θ
I
ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɫɨɨɬɧɨɲɟɧɢɹ
ɇɟɨɛɯɨɞɢɦɵɟ ɢ ɞɨɫɬɚɬɨɱɧɵɟ ɭɫɥɨɜɢɹ ɭɫɬɨɣɱɢɜɨɫɬɢ ɪɚɜɧɨɜɟɫɢɹ ɢɡɜɟɫɬɧɵ ɤɚɤ ɤɪɢɬɟɪɢɣ
Ɋɚɭɫɚ-Ƚɭɪɜɢɰɚ, ɢɦɟɧɧɨ: (i) ɚ
i
> 0; ɢ (ii) a
1
a
2
— a
3
> 0. Ʉɚɤ ɩɨɤɚɡɚɧɨ ɜ ɪɚɛɨɬɚɯ Ȼɟɧɯɚɛɢɛɚ-
Ɇɢɣɚɨ (1981) ɢ Ɂɚɧɝɚ (1990b), ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɡɧɚɱɟɧɢɣ ɩɚɪɚɦɟɬɪɨɜ ɪɚɜɧɨɜɟɫɢɟ
ɢɫɫɥɟɞɭɟɦɨɣ ɧɚɦɢ ɫɢɫɬɟɦɵ ɦɨɠɟɬ ɨɤɚɡɚɬɶɫɹ ɤɚɤ ɭɫɬɨɣɱɢɜɵɦ, ɬɚɤ ɢ ɧɟɭɫɬɨɣɱɢɜɵɦ.
ɇɚɩɪɢɦɟɪ, ɟɫɥɢ ɦɵ ɞɜɢɠɟɦɫɹ ɨɬ ɚɞɚɩɬɢɜɧɵɯ ɨɠɢɞɚɧɢɣ ɜ ɫɬɨɪɨɧɭ ɬɨɱɧɨɝɨ ɩɪɟɞɜɢɞɟɧɢɹ,
ɦɨɠɟɬ ɜɨɡɧɢɤɧɭɬɶ ɧɟɭɫɬɨɣɱɢɜɚɹ ɫɟɞɥɨɜɚɹ ɬɨɱɤɚ. ɑɬɨɛɵ ɩɪɨɢɥɥɸɫɬɪɢɪɨɜɚɬɶ ɷɬɨ ɭɬɜɟɪɠɞɟɧɢɟ,
ɪɚɫɫɦɨɬɪɢɦ, ɱɬɨ ɩɪɨɢɫɯɨɞɢɬ ɜ ɬɨɱɤɟ ɪɚɜɧɨɜɟɫɢɹ
ɩɪɢ ɜɨɡɪɚɫɬɚɧɢɢ ɨɛɴɟɦɚ ɞɟɧɟɠɧɨɣ ɦɚɫɫɵ.
ɇɟɦɟɞɥɟɧɧɵɦ ɫɥɟɞɫɬɜɢɟɦ ɷɬɨɝɨ ɹɜɥɹɟɬɫɹ ɩɨɜɵɲɟɧɢɟ ɭɪɨɜɧɹ ɰɟɧ, ɢ ɪɟɚɥɶɧɵɣ ɨɛɴɟɦ
ɞɟɧɟɠɧɵɯ ɡɚɩɚɫɨɜ ɫɬɪɟɦɢɬɫɹ ɜɨɡɜɪɚɬɢɬɶɫɹ ɤ ɩɪɟɠɧɟɦɭ ɭɪɨɜɧɸ, ɨɞɧɚɤɨ ɩɟɪɜɨɧɚɱɚɥɶɧɨɟ
ɜɨɡɪɚɫɬɚɧɢɟ ɞɟɧɟɠɧɨɣ ɦɚɫɫɵ ɩɪɢɜɨɞɢɬ ɤ ɩɨɜɵɲɟɧɢɸ ɰɟɧɨɜɵɯ ɨɠɢɞɚɧɢɣ ɢ ɫɧɢɠɚɟɬ
ɧɚɤɨɩɥɟɧɧɵɣ ɤɚɩɢɬɚɥ. Ɉɛɚ ɩɨɫɥɟɞɧɢɯ ɷɮɮɟɤɬɚ ɜɵɡɵɜɚɸɬ ɩɚɞɟɧɢɟ ɞɟɧɟɠɧɨɝɨ ɩɪɟɞɥɨɠɟɧɢɹ ɢ
ɦɨɝɭɬ ɫɬɚɹɬɶ ɩɪɢɱɢɧɨɣ ɬɨɝɨ, ɱɬɨ ɨɛɴɟɦ ɞɟɧɟɠɧɵɯ
ɡɚɩɚɫɨɜ ɛɭɞɟɬ ɩɪɟɜɵɲɚɬɶ ɫɜɨɟ ɪɚɜɧɨɜɟɫɧɨɟ
ɡɧɚɱɟɧɢɟ. ȿɫɥɢ ɞɟɧɟɠɧɨɟ ɩɪɟɞɥɨɠɟɧɢɟ ɩɪɨɞɨɥɠɚɟɬ ɩɚɞɚɬɶ ɧɢɠɟ ɭɪɨɜɧɹ ɪɚɜɧɨɜɟɫɢɹ,
ɩɟɪɟɦɟɧɧɵɟ ɦɟɧɹɸɬɫɹ ɦɟɫɬɚɦɢ:
ɨɛɴɟɦ ɧɚɤɨɩɥɟɧɢɣ ɤɚɩɢɬɚɥɚ ɜɨɡɪɚɫɬɚɟɬ, ɚ ɨɠɢɞɚɧɢɹ ɫɧɢɠɚɸɬɫɹ. ȼ ɫɨɱɟɬɚɧɢɢ ɫ ɩɪɹɦɵɦ
ɜɥɢɹɧɢɟɦ ɨɛɴɟɦɚ ɞɟɧɟɠɧɵɯ ɡɚɩɚɫɨɜ ɧɚ ɞɟɧɟɠɧɵɟ ɧɚɤɨɩɥɟɧɢɹ ɷɬɨ ɩɪɢɜɟɞɟɬ ɬɟɩɟɪɶ ɤ
ɢɡɦɟɧɟɧɢɸ ɧɚɩɪɚɜɥɟɧɢɹ ɞɢɧɚɦɢɤɢ ɞɟɧɟɠɧɵɯ ɡɚɩɚɫɨɜ. ɗɬɢ ɫɨɨɛɪɚɠɟɧɢɹ ɧɚɜɨɞɹɬ ɧɚɫ ɧɚ
ɦɵɫɥɶ
ɨ ɜɨɡɦɨɠɧɨɫɬɢ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɞɨɥɝɨɜɪɟɦɟɧɧɵɯ ɨɫɰɢɥɥɹɰɢɢ.
Ⱦɨɤɚɡɚɬɟɥɶɫɬɜɨ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɛɢɮɭɪɤɚɰɢɢ ɏɨɩɮɚ ɜ ɨɛɨɛɳɟɧɧɨɣ ɦɨɞɟɥɢ Ɍɨɛɢɧɚ
ɩɪɢɧɚɞɥɟɠɢɬ Ȼɟɧɯɚɛɢɛɭ ɢ Ɇɢɣɚɨ (1981). ɂɯ ɪɟɡɭɥɶɬɚɬɵ ɦɨɠɧɨ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɜ ɜɢɞɟ
ɫɥɟɞɭɸɳɟɣ ɬɟɨɪɟɦɵ:
Ɍɟɨɪɟɦɚ 5.5.1. ȿɫɥɢ ɫɭɳɟɫɬɜɭɟɬ ɬɚɤɨɣ ɧɚɛɨɪ ɡɧɚɱɟɧɢɣ ɩɚɪɚɦɟɬɪɨɜ, ɤɨɬɨɪɵɣ ɨɛɟɫɩɟɱɢɜɚɟɬ
ɭɫɬɨɣɱɢɜɨɫɬɶ ɪɚɜɧɨɜɟɫɢɹ, ɦɨɠɧɨ ɧɚɣɬɢ ɬɚɤɨɟ ɡɧɚɱɟɧɢɟ
β
0
, ɩɪɢ ɤɨɬɨɪɨɦ ɹɤɨɛɢɚɧ ɫɢɫɬɟɦɵ
ɢɦɟɟɬ ɩɚɪɭ ɱɢɫɬɨ ɦɧɢɦɵɯ ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ. Ȼɨɥɟɟ ɬɨɝɨ, ɫɭɳɟɫɬɜɭɟɬ ɧɟɩɪɟɪɵɜɧɚɹ
ɮɭɧɤɰɢɹ v(
ε
)[v(0) = 0] ɩɚɪɚɦɟɬɪɚ
ε
, ɬɚɤɚɹ, ɱɬɨ ɤɨɝɞɚ ɩɚɪɚɦɟɬɪ
ε
ɞɨɫɬɚɬɨɱɧɨ ɦɚɥ, ɨɛɨɛɳɟɧɧɚɹ
ɦɨɞɟɥɶ Ɍɨɛɢɧɚ ɢɦɟɟɬ ɧɟɩɪɟɪɵɜɧɨɟ ɫɟɦɟɣɫɬɜɨ ɩɟɪɢɨɞɢɱɟɫɤɢɯ ɪɟɲɟɧɢɣ (k(t,
ε
), x(t,
ε
), q(t,
ε
))
T
,
ɤɨɬɨɪɨɟ ɩɪɢ
ε
ĺ 0 ɫɬɹɝɢɜɚɟɬɫɹ ɤ ɬɨɱɤɟ ɪɚɜɧɨɜɟɫɢɹ (k
0
, ɯ
0
, q
0
).
ɗɬɚ ɬɟɨɪɟɦɚ ɜɟɫɶɦɚ ɜɚɠɧɚ, ɬɚɤ ɤɚɤ ɞɨɤɚɡɵɜɚɟɬ ɫɭɳɟɫɬɜɨɜɚɧɢɟ ɪɟɝɭɥɹɪɧɵɯ ɤɨɥɟɛɚɧɢɣ ɜ
ɫɢɫɬɟɦɟ. ȿɫɥɢ ɰɢɤɥ ɭɫɬɨɣɱɢɜ, ɬɚɤɢɟ ɤɨɥɟɛɚɧɢɹ ɛɭɞɭɬ ɩɪɨɞɨɥɠɚɬɶɫɹ ɛɟɫɤɨɧɟɱɧɨ ɞɨɥɝɨ. Ɍɚɤɢɦ
ɨɛɪɚɡɨɦ, ɧɟɪɚɜɧɨɜɟɫɧɨɟ ɷɤɨɧɨɦɢɱɟɫɤɨɟ ɪɚɡɜɢɬɢɟ ɨɬɧɵɧɟ ɧɟ ɫɥɟɞɭɟɬ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ
ɛɵɫɬɪɨɬɟɤɭɳɢɣ ɩɪɨɰɟɫɫ, ɢ ɨɛɨɛɳɟɧɧɚɹ ɦɨɞɟɥɶ Ɍɨɛɢɧɚ ɫɬɚɧɨɜɢɬɫɹ ɩɪɢɝɨɞɧɨɣ ɞɥɹ ɨɩɢɫɚɧɢɹ
ɞɟɥɨɜɵɯ ɰɢɤɥɨɜ. Ɇɵ ɩɪɨɞɨɥɠɢɦ ɢɫɫɥɟɞɨɜɚɧɢɟ Ȼɟɧɯɚɛɢɛɚ ɢ Ɇɢɣɚɨ ɫ
ɬɟɦ, ɱɬɨɛɵ (i) ɧɚɣɬɢ
ɭɫɥɨɜɢɹ ɭɫɬɨɣɱɢɜɨɫɬɢ ɰɢɤɥɨɜ; (ii) ɞɚɬɶ ɬɨɱɧɭɸ ɢɧɬɟɪɩɪɟɬɚɰɢɸ ɩɚɪɚɦɟɬɪɚ
ε
; (iii) ɧɚɣɬɢ ɹɜɧɨɟ
ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɰɢɤɥɢɱɟɫɤɢɯ ɬɪɚɟɤɬɨɪɢɣ; (iv)
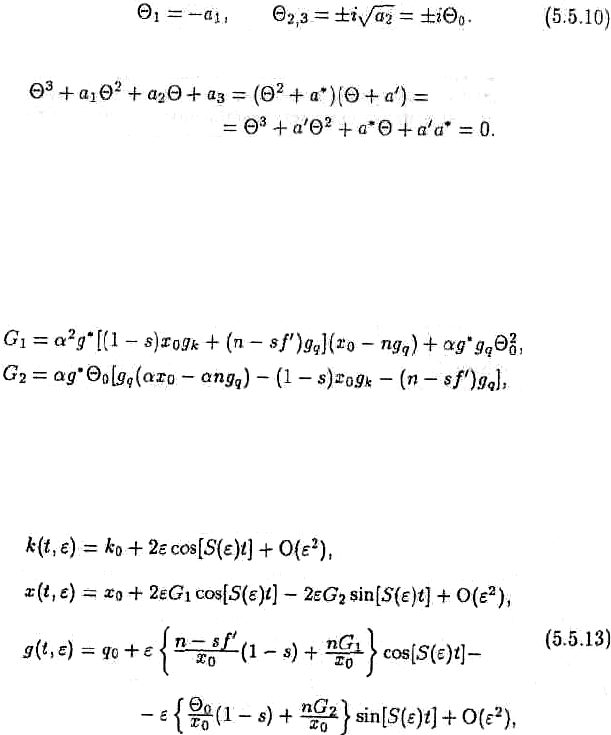
ɱɬɨɛɵ ɨɩɪɟɞɟɥɢɬɶ, ɜ ɤɚɤɢɯ ɫɥɭɱɚɹɯ ɛɢɮɭɪɤɚɰɢɹ ɏɨɩɮɚ ɹɜɥɹɟɬɫɹ ɫɭɩɟɪɤɪɢɬɢɱɟɫɤɨɣ ɥɢɛɨ
ɫɭɛɤɪɢɬɢɱɟɫɤɨɣ. ɉɪɟɠɞɟ ɜɫɟɝɨ, ɩɨɤɚɠɟɦ, ɱɬɨ ɟɫɥɢ ɹɤɨɛɢɚɧ ɢɦɟɟɬ ɩɚɪɭ ɱɢɫɬɨ ɦɧɢɦɵɯ
ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ, ɬɨ ɜɫɟ ɬɪɢ ɡɚɞɚɸɬɫɹ ɮɨɪɦɭɥɚɦɢ
Ʉɚɤ ɭɫɬɚɧɨɜɥɟɧɨ Ȼɟɧɯɚɛɢɛɨɦ ɢ Ɇɢɣɚɨ, ɜɫɟ ɚ
i
(i = 1, 2, 3) ɩɨɥɨɠɢɬɟɥɶɧɵ. ɇɚɥɢɱɢɟ ɱɢɫɬɨ
ɦɧɢɦɵɯ ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ ɨɡɧɚɱɚɟɬ, ɱɬɨ (5.5.9) ɦɨɠɧɨ ɩɟɪɟɩɢɫɚɬɶ ɤ ɫɥɟɞɭɸɳɟɦɭ ɜɢɞɭ:
(5.5.11)
ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɫɨɨɬɧɨɲɟɧɢɹ (5.5.10) ɫɩɪɚɜɟɞɥɢɜɵ.
ɉɨɫɥɟɞɭɸɳɢɣ ɚɧɚɥɢɡ ɢɫɩɨɥɶɡɭɟɬ
β
ɜ ɤɚɱɟɫɬɜɟ ɛɢɮɭɪɤɚɰɢɨɧɧɨɝɨ ɩɚɪɚɦɟɬɪɚ. Ɂɧɚɱɟɧɢɟ
β
,
ɤɨɬɨɪɨɟ ɭɞɨɜɥɟɬɜɨɪɹɟɬ (5.5.11), ɨɛɨɡɧɚɱɢɦ ɤɚɤ
β
0
, ɚ ɦɚɥɨɟ ɨɬɤɥɨɧɟɧɢɟ
β
ɨɬ
β
0
ɤɚɤ v, ɬ.ɟ. v =
β
—
β
0
. ɋɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɹɜɥɹɸɬɫɹ ɧɟɩɪɟɪɵɜɧɵɦɢ ɮɭɧɤɰɢɹɦɢ ɩɚɪɚɦɟɬɪɚ
β
. Ɉɛɨɡɧɚɱɢɦ
ɱɟɪɟɡ Θ(v) ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ, ɪɚɜɧɨɟ iΘ
0
ɜ ɬɨɱɤɟ v = 0 (ɬ.ɟ.
β
=
β
0
). Ɇɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ
ɜɩɨɥɧɟ ɪɚɡɭɦɧɨ ɫɱɢɬɚɬɶ Θ
v
(0) ɧɟ ɪɚɜɧɵɦ ɧɭɥɸ (ɫɦ. Ȼɟɧɯɚɛɢɛ ɢ Ɇɢɣɚɨ, 1981).
ȼɜɟɞɟɦ ɫɥɟɞɭɸɳɢɟ ɞɟɣɫɬɜɢɬɟɥɶɧɵɟ ɜɟɥɢɱɢɧɵ:
(5.5.12)
ɝɞɟ J* = 1/[(1 — s){
2
0
Θ + (αɯ
0
— αɩJ
q
)
2
}]. Ɇɨɠɧɨ ɞɨɤɚɡɚɬɶ ɫɥɟɞɭɸɳɭɸ ɬɟɨɪɟɦɭ.
Ɍɟɨɪɟɦɚ 5.5.2. Ȼɢɮɭɪɤɚɰɢɨɧɧɵɣ ɰɢɤɥ ɜ ɨɛɨɛɳɟɧɧɨɣ ɦɨɞɟɥɢ Ɍɨɛɢɧɚ ɢɦɟɟɬ ɩɟɪɢɨɞ 2π/S(
ε
)
ɢ ɦɨɠɟɬ ɛɵɬɶ ɩɪɢɛɥɢɠɟɧɧɨ ɨɩɢɫɚɧ ɮɨɪɦɭɥɚɦɢ
