Загиров Н.Н. Теория обработки металлов давлением
Подождите немного. Документ загружается.


51
Большую роль в теории пластичности играет второй инвариант I
2
(D
ξ
).
Неотрицательную величину, составленную из второго инварианта девиатора
скорости деформации
)(2
2 ξ
= DIH
, (10.7)
называют интенсивностью скоростей деформации сдвига.
Легко показать, что для Н можно воспользоваться формулой:
( ) ( )
( )
[
]
( )
( ) ( ) ( )
2
1133
2
3322
2
2211
222
222
2
3
2
6
3
2
2
ξ−ξ+ξ−ξ+ξ−ξ=ξ+ξ+ξ+
+ξ−ξ+ξ−ξ+ξ−ξ==
ξ
xzyzxy
zzxxzzyyyyxx
)D(IH
(10.8)
Контрольные вопросы
1. Какой имеют механический смысл и как называются компоненты тензора
скорости деформации?
2. В чем состоит механический смысл первого инварианта тензора скорости
деформации?
3. Приведите формулы трех базовых инвариантов тензора скорости
деформации.
4. Дайте определение девиатора скорости деформации.
5. Чему равен первый инвариант девиатора скорости деформации?
6. Что характеризует девиатор скорости деформации?
7. Что называется интенсивностью скорости деформации сдвига?
8. Разъясните кинематический смысл шарового тензора и девиатора
скоростей деформации. Когда D
ξ
и T
ξ
совпадают?
9. Что такое степень деформации сдвига?

52
ЛЕКЦИЯ 11
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ НЕРАЗРЫВНОСТИ.
УРАВНЕНИЯ ТРАЕКТОРИИ ПЕРЕМЕЩЕНИЯ
И УСКОРЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
План лекции:
1. Дифференциальное уравнение неразрывности.
2. Условие несжимаемости материала.
3. Параметрические уравнения траектории перемещения частицы.
4. Формулы, определяющие проекции вектора ускорения движения
материальной точки.
5. Теория течения в приращениях перемещений.
6. Тензор приращений деформаций.
7. Степень деформации сдвига.
Деформируемый материал обладает массой, которая в соответствии с
законом сохранения вещества в процессе обработки остается постоянной, т.е.
m = ρV = const, (11.1)
где ρ = ρ(x, y, z) – массовая плотность, которая может изменяться во
времени, так как материалы уплотняются или разрыхляются;
V – объем деформируемого тела.
Продифференцируем выражение (11.1) по времени.
0
d
d
d
d
d
d
=ρ+=
t
V
V
t
S
t
m
. (11.2)
Производная
t
V
d
d
, входящая в выражение (11.2), представляет скорость
абсолютного изменения объема, рассчитываемую по формуле:
V
t
V
ρ=
d
d
. (11.3)
53
После подстановки (11.3) в (11.2) и сокращения на V, получим
выражение:
0
d
d
=ρξ+
ρ
t
, (11.4)
называемое дифференциальным уравнением неразрывности.
Если учесть, что ξ = ξ
ii
= υ
i,i
, тогда имеем
0
d
d
=ρυ+
ρ
i,i
t
.
В частном случае деформации материала, плотность которого не
изменяется (ρ = const), уравнение неразрывности превращается в условие:
0=ξ+ξ+ξ=
∂
υ∂
+
∂
υ
∂
+
∂
υ∂
=υ
zzyyxx
z
y
x
i,i
zyx
, (11.5)
которое называют условием не сжимаемости или постоянства объема.
Другая форма записи данного условия ξ = 0.
По известному полю скоростей можно установить траектории
движения частиц и конечные перемещения U
x
, U
y
, U
z
.
Пусть какая-нибудь материальная частица при t = 0 имела координаты x
0
, y
0
,
z
0
, а при t > 0 – x, y, z. Скорости движения материальной частицы:
t
x
x
d
d
=υ
;
t
y
y
d
d
=υ
;
t
z
z
d
d
=υ
.
Следовательно, имеем три обыкновенных дифференциальных уравнения:
)t,z,y,x(
t
x
x
υ=
d
d
;
)t,z,y,x(
t
y
y
υ=
d
d
; (11.6)
)t,z,y,x(
t
z
z
υ=
d
d
.

54
При начальных условиях t = 0: x = x
0
, y = y
0
, z = z
0
.
Поскольку скорости υ
i
известны, т.е. известны правые части уравнения
(11.6), то интегрируя их, можно получить:
U
x
= x – x
0
= f
1
(x
0
, y
0
, z
0
, t);
U
y
= y – y
0
= f
2
(x
0
, y
0
, z
0
, t); (11.7)
U
z
= z – z
0
= f
3
(x
0
, y
0
, z
0
, t).
Формулы (11.7) называют параметрическими уравнениями траектории
перемещения материальной частицы при деформировании, позволяющими
отыскать форму и размеры тела в конечный момент времени t.
Дифференцируя сложную функцию, получим:
t
z
zt
y
yt
x
xtt
iiiii
i
d
d
d
d
d
d
d
d
⋅
∂
υ
∂
+⋅
∂
υ
∂
+⋅
∂
υ
∂
+
∂
υ
∂
=
υ
=ω
. (11.8)
Вычисленное ускорение материальной частицы входит в уравнения
движения сплошной среды, о которых речь шла в лекции 8.
Рассмотрим некоторый момент времени t. Введем малый, но конечный
промежуток времени dt, за который частица материала получила приращения
перемещений:
dU
x
= υ
x
dt; dU
y
= υ
y
dt; dU
z
= υ
z
dt.
Если в этот момент времени t известны компоненты тензора скорости
деформации ξ
ii
, то можно рассчитать приращения деформации, которые
приобрела частица за время dt:
dε
ij
= ξ
ij
dt. (11.9)
Таким образом, деформированное состояние в окрестности точки
характеризуется симметричным тензором приращения деформации:
εεε
εεε
εεε
=
ε
zzzyzx
yzyyyx
xzxyxx
T
ddd
ddd
ddd
d
(11.10)

55
для которого
)d(d
2
1
dd
ijjijiij
,U,U +=ε=ε
.
В развернутой форме:
xxx
U
x
dd
∂
∂
=ε
;
yyy
U
y
dd
∂
∂
=ε ;
zzz
U
z
dd
∂
∂
=ε
;
∂
∂
+
∂
∂
=ε
yxxy
U
x
U
y
dd
2
1
d ;
∂
∂
+
∂
∂
=ε
zyyz
U
y
U
z
dd
2
1
d ;
∂
∂
+
∂
∂
=ε
zxxz
U
x
U
z
dd
2
1
d
.
Тензор приращений деформаций, как и T
ξ
, характеризует мгновенное
деформированное состояние, поэтому свойства его аналогичны свойствам T
ξ
.
Остановимся лишь на отдельных величинах, составленных из компонентов
T
dε
.
Первый инвариант тензора приращения деформации выражает
приращение относительного приращения объема:
I
1
(T
dS
) = dε
xx
+ dε
yy
+ dε
zz
= dε. (11.11)
Девиатор приращения деформации
ED ε−=
ε
d
3
1
d
. (11.12)
Приращением степени деформации сдвига некоторой частицы за время
dt называют величину, подсчитываемую по формуле:
(
)
ε
=λ
d2
2d DI
. (11.13)

56
Величину, определяемую формулой
∫
ττ=λ
t
H
0
)d(
, (11.14)
в которой интегрирование производится вдоль траектории движения
частицы, называют степенью деформации сдвига.
Контрольные вопросы
1. Какой закон положен в основу вывода дифференциального уравнения
неразрывности?
2. Как подсчитать ускорение частиц сплошной среды, если задано векторное
поле скорости течения?
3. Составьте дифференциальное уравнение траектории движения
материальной частицы.
4. Что такое траектория движения частиц?
5. В чем разница тензора приращения деформации и тензора деформации?
6. Как подсчитать главные удлинения, если главные оси в процессе
деформации сохраняют свое направление?
7. Как подсчитать ускорение частиц сплошной среды, если задано векторное
поле скорости течения?
ЛЕКЦИЯ 12
ФИЗИЧЕСКИЕ УРАВНЕНИЯ СВЯЗИ
НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЙ
План лекции:
1. Формулировка общих физических уравнений связи напряженного и
деформированного состояний для изотропных материалов.
2. Реологические модели сред.
3. Уравнения связи для некоторых моделей сред, характерных для холодной
и горячей обработки давлением.
Будем считать, что в задачу теории пластичности входит определение
напряженного и деформированного состояний в любой момент времени t в

57
любой точке обрабатываемого тела объемом V с ограничивающей его
поверхностью S.
Другими словами, задачей теории пластичности является определение
десяти функций:
σ
ij
= σ
ij
(x, y, z, t);
x = x (x
0
, y
0
, z
0
, t);
y = y (x
0
, y
0
, z
0
, t); (12.1)
z = z (x
0
, y
0
, z
0
, t);
ρ = ρ (x, y, z, t),
которые должны быть найдены в объеме деформируемого тела V вместе с его
границей S в любой момент времени t и которые называют искомыми
механическими переменными.
Функции (12.1) не могут быть любыми. Они связаны
дифференциальными уравнениями движения и дифференциальным
уравнением неразрывности:
=ρυ+
ρ
ρω=ρ+σ
0
d
d
i,i
iij,ij
t
g
(12.2)
Для замыкания полной системы уравнений недостает шести уравнений,
которые в механике сплошных сред формулируют исходя из свойств
конкретной среды. В теории пластичности эти шесть уравнений носят
название физических уравнений связи напряженного и деформированного
состояний.
Рассмотрим вопрос о формулировке общих физических уравнений для
изотропных материалов, т.е. материалов, механические свойства которых в
различных направлениях одинаковы.
Напряжения σ
ij
и скорости деформации ξ
ij
связаны между собой
некоторыми неизвестными пока функциями
σ
ij
= f
ij
(ξ
kl
). (12.3)
Эти функции не могут быть любыми, для них должны выполняться: а)
условие сохранения тензорной размерности, т.е. функция f должна

58
преобразовать тензор второй валентности в тензор второй валентности; б)
условие сохранение симметрии, т.е. функция f должна преобразовывать
симметричный тензор в симметричный тензор.
В прикладной теории пластичности, рассматривающей
технологические задачи деформации металлов, принимается гипотеза
(точнее, допущение) об изотропии деформируемого материала: материал на
любом уровне размера элементарного объема обладает изотропными
механическими свойствами.
Из допущения об изотропии вытекает важная гипотеза о
коаксиальности (соосности) тензоров напряжений и скоростей деформации:
направления главных нормальных напряжений и главных скоростей
относительных удлинений совпадают. Эта гипотеза не справедлива в случае
деформации анизотропных материалов – таких, у которых механические
свойства зависят от направления.
Специальные опыты показывают, что с достаточной для многих
случаев степенью точности имеет место пропорциональность компонентов
девиаторов напряжения и скорости деформации. Это положение в теории
пластичности носит название гипотезы пропорциональности девиаторов
напряжения и скорости деформации.
Таким образом, из гипотезы пропорциональности или гипотезы
подобия девиаторов напряжения и скорости деформации следует:
D
σ
= ψD
ξ
;
)
3
1
(
ijijijij
ξδ−ξψ=σδ−σ , (12.4)
где ψ – скалярный множитель.
Величину ψ можно выразить через известные инварианты:
H
T2
=ψ , (12.5)
где Т – интенсивность касательных напряжений, определяемая по формуле
(6.8);
Н – интенсивность скоростей деформации сдвига, определяемая по
формуле (10.8).

59
Могут ли выражения (12.4) служить искомыми физическими
уравнениями (их должно быть шесть)? В системе (12.4) независимых
уравнений пять. Кроме того, в уравнения (12.4) введена еще одна неизвестная
величина ψ. Следовательно, для замыкания системы уравнений теории
пластичности ее следует дополнить еще двумя соотношениями.
Первым соотношением служит связь первых инвариантов тензоров
напряжения и скорости деформации:
σ = σ(ξ, …). (12.6)
Второе соотношение, определяемое из опытов – это связь между
интенсивностью касательных напряжений Т и интенсивностью скоростей
деформации сдвига Н:
Т = Т(Н, …). (12.7)
Точки в выражениях (12.6) и (12.7) означают, что эти функции могут
содержать в качестве аргументов еще иные инвариантные характеристики
напряженно-деформированного состояния.
Экспериментальному определению функций (12.6) и (12.7) помогает
гипотеза единой кривой: функции Т = Т(Н) и σ = σ(ξ), связывающие
инвариантные характеристики напряженного и деформированного состояний
и определяемые экспериментально, не зависят от вида деформации
(растяжение, сжатие, кручение и т.п.) и напряженного состояния, и находят
их в простейших опытах, а результаты могут быть распространены на общий
случай.
Установление уравнений состояния для пластически деформируемой
среды является разделом реологии, а сами уравнения состояния называются
реологическими моделями. Их составляют для линейного напряженного
состояния на основании идеализации истинных диаграмм растяжения и
диаграмм деформирования с учетом эффектов, сопровождающих
пластическую деформацию и наиболее существенных свойств
деформируемой среды.
60
Рассмотрим некоторые модели, характерные для холодной и горячей
обработки давлением.
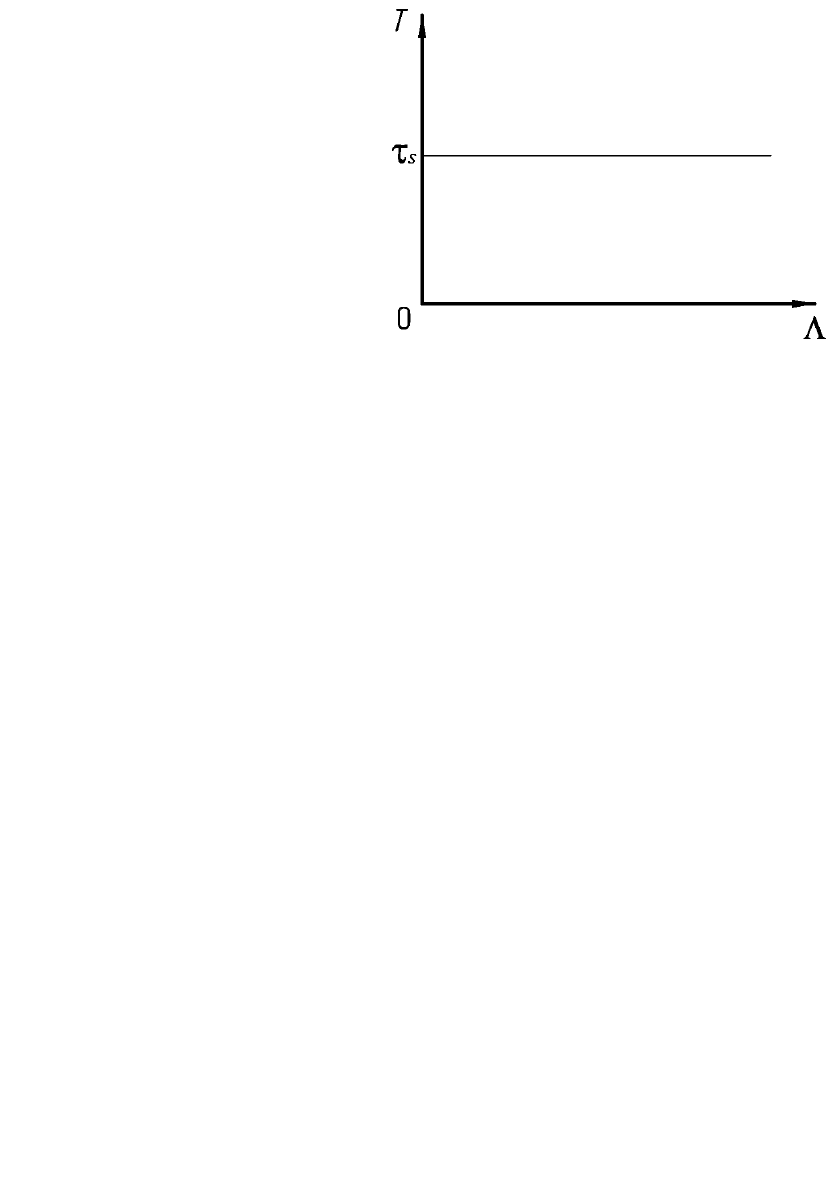
1. Идеальная жестко-пластическая среда.
Деформация начинается, когда интенсивность касательных
напряжений достигнет критического значения τ
S
(сопротивления деформации
сдвига), далее деформация продолжается при Т = τ
S
= const (рис. 12.1).
Рис. 12.1. Зависимость, отражающая модель идеальной жестко-пластичной среды
В этой модели пренебрегают упрочнением материала и упругой
деформацией, читая ее бесконечно малой по сравнению с пластической.
2. Жестко-пластическая среда с деформированным упрочнением (рис. 12.2 а,
б) развивает предыдущую модель и позволяет учесть наклеп при холодной
обработке давлением. Вариант «б» используют в задачах с небольшим
диапазоном деформаций, когда допустимо криволинейный график «а»
приближенно представить в виде ломаной линии. В случае «б» модель
поведения материала записывают в виде:
Т = τ
S
+ аλ,
где а – модуль упрочнения.
