Загиров Н.Н. Теория обработки металлов давлением
Подождите немного. Документ загружается.

41
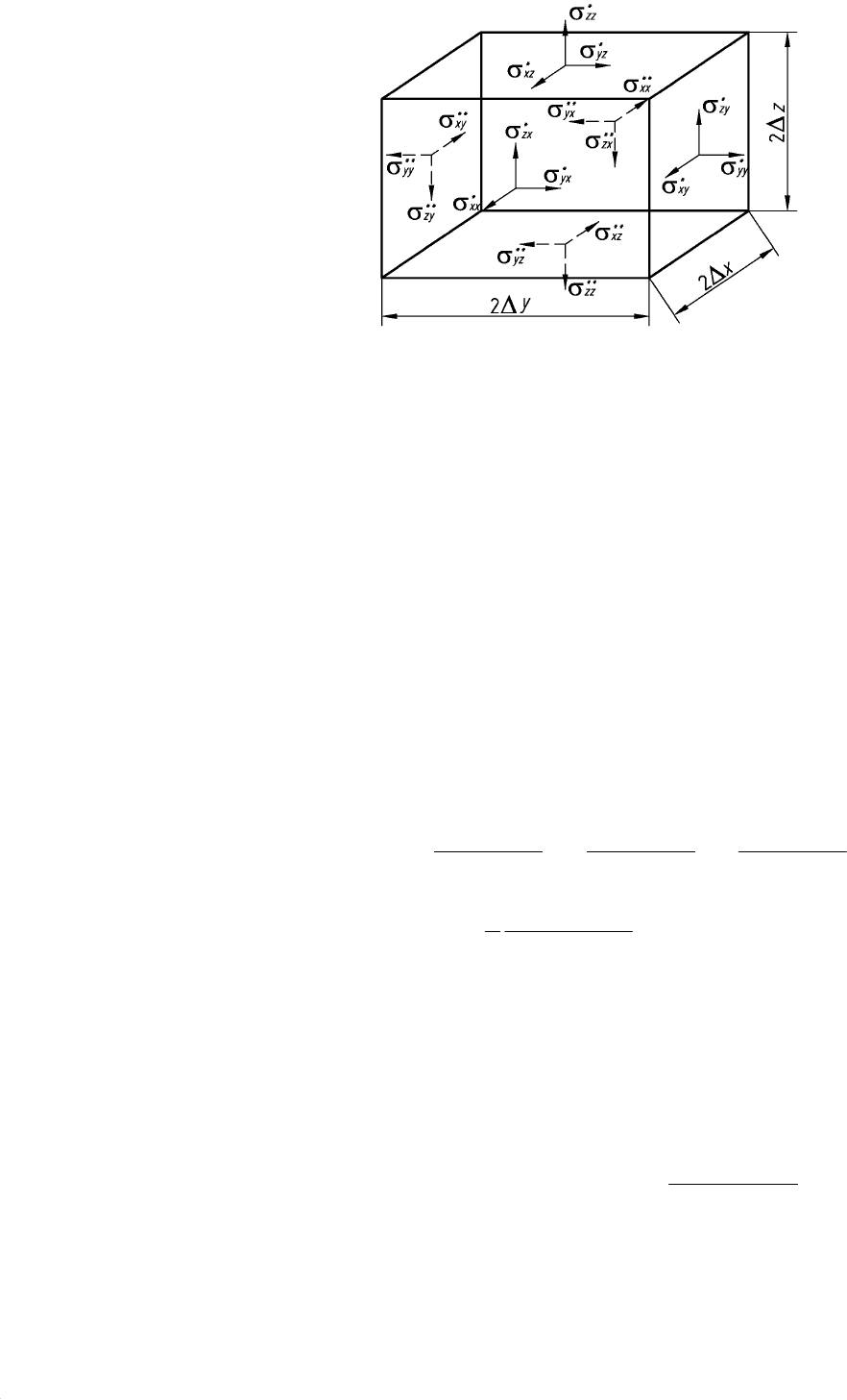
Рис. 8.1. Схема к установлению связи между компонентами тензора напряжений
Рассмотрим напряжения, действующие на площадках,
перпендикулярных оси x:
)z,y,x(
ixix
σ
=
σ
;
)z,y,xx(
ix
*
ix
∆+σ=σ
;
)z,y,xx(
ix
**
ix
∆−σ=σ .
Подставив значения напряжений в формулу Тейлора, получим
...a
x
)z,y,x(f
c
z
)z,y,x(f
b
y
)z,y,x(f
a
x
)z,y,x(f
)z,y,x(f
)
c
z
,
b
y
,
a
x
(
f
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+=
=
+
+
+
2
2
2
2
1
При разложении в ряд Тейлора σ
ix
появляются величины высшего
порядка малости (больше первого), которыми можно пренебречь. В итоге
получим:
x
x
)z,y,x(
)z,y,x()z,y,xx(
ix
ixix
∆
∂
σ
∂
+σ=∆+σ .

42
В сокращенном виде эту формулу можно записать
x
x
ix
ix
*
ix
∆
∂
σ
∂
+σ=σ .
Напряжение
**
ix
σ рассчитывают по формуле
x
x
ix
ix
**
ix
∆
∂
σ
∂
−σ=σ .
Аналогично можно найти составляющие напряжения:
y
y
iy
iy
*
iy
∆
∂
σ
∂
+σ=σ
;
y
y
iy
iy
**
iy
∆
∂
σ
∂
−σ=σ ; (8.1)
z
z
iz
iz
*
iz
∆
∂
σ
∂
+σ=σ ;
z
z
iz
iz
**
iz
∆
∂
σ
∂
−σ=σ .
Для дальнейшего вывода воспользуемся уравнениями поступательного
движения:
∑
ω
=
xx
mF
; (8.2 а)
∑
ω
=
yy
mF
; (8.2 б)
∑
ω
=
zz
mF
, (8.2 в)
где
∑
i
F - сумма проекций всех сил, действующих на параллелепипед
(включая силу тяжести), на соответствующую ось координат;
z
y
x
V
m
∆
⋅
∆
⋅
∆
⋅
ρ
=
∆
⋅
ρ
=
2
2
2
- его масса;
ω
i
- составляющие вектора ускорения.

43
Рассмотрим уравнение (8.2 а), при составлении которого получим
следующее выражение:
xx
**
xz
*
xz
**
xy
*
xy
**
xx
*
xx
mmgyxyx
zxzxzyzy
ω=+∆∆σ−∆∆σ+
+∆∆σ−∆∆σ+∆∆σ−∆∆σ
2222
22222222
(8.3)
Используя формулы (8.1), после сокращения на 2∆x2∆y2∆z, выражение
(8.3) записывают в виде:
xx
xz
xy
xx
g
zyx
ρω=ρ+
∂
σ∂
+
∂
σ
∂
+
∂
σ∂
. (8.4 а)
Аналогично можно получить остальные уравнения:
yy
yzyyyx
g
zyx
ρω=ρ+
∂
σ
∂
+
∂
σ
∂
+
∂
σ
∂
; (8.4 б)
zz
zz
zy
zx
g
zyx
ρω=ρ+
∂
σ∂
+
∂
σ
∂
+
∂
σ∂
. (8.4 в)
Уравнения (8.4) называют дифференциальными уравнениями движения,
более кратко их записывают в виде:
σ
ij,j
+ ρg
i
= ρω
i
.
Уравнения (8.4) не образуют пока замкнутой системы, пригодной для
решения, так как три уравнения связывают десять неизвестных функций:
шесть для σ
ij
, три ω
i
, а также плотность ρ.
Большинству процессов обработки металлов давлением свойственно
то, что удельные массовые силы
g
и ускорения
ω
достаточно малы и ими
можно пренебречь. Тогда уравнения (8.4) превращаются в
дифференциальные уравнения равновесия:
0=
∂
σ∂
+
∂
σ
∂
+
∂
σ∂
zyx
xz
xy
xx
;

44
0=
∂
σ
∂
+
∂
σ
∂
+
∂
σ
∂
zyx
yzyyyx
; (8.5)
0=
∂
σ∂
+
∂
σ
∂
+
∂
σ∂
zyx
zz
zy
zx
,
или кратко:
σ
ij,j
= 0.
Контрольные вопросы
1. Какими уравнениями определяется связь между компонентами,
определяющими поле тензора напряжения?
2. Чем отличаются дифференциальные уравнения движения от
дифференциальных уравнений равновесия?
3. Что такое массовые силы?
ЛЕКЦИЯ 9
ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА
План лекции:
1. Деформированное состояние в точке тела.
2. Перемещение частиц тела.
3. Тензор абсолютной производной векторного поля скорости перемещения.
4. Разложение его на тензор скорости деформации и тензор вращения.
Известно, что движение твердого недеформируемого тела можно
представить суммой поступательного и вращательного движений. Если же
тело деформируется, то движение будет сложным.
При фиксированном моменте деформации t перемещение частиц тела
определяется полем вектора скорости перемещения материальных частиц
υ
.
Рассмотрим точку М деформируемого тела, положение которой можно
задать координатами x, y, z (рис. 9.1).
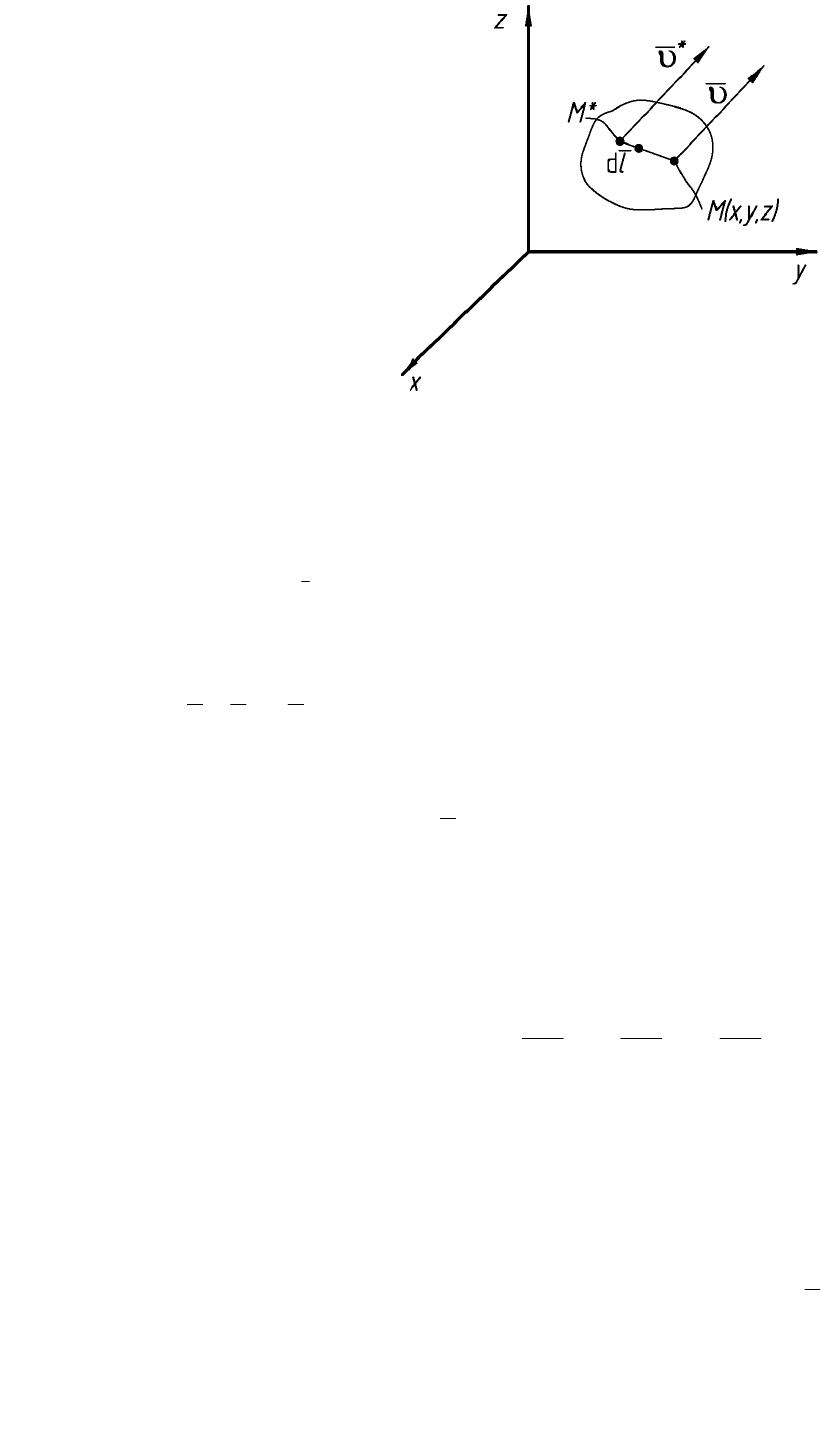
45
Рис. 9.1. Схема перемещения некоторой материальной частицы деформируемого тела
Бесконечно малая окрестность окружает точку М. Положение
произвольной точки М
*
в этой окрестности можно задать дополнительным
вектором
l
d
с координатами dx, dy, dz.
Пусть в точке М скорость перемещения частиц υ = (υ
x
, υ
y
, υ
z
). Скорости
в точке М
*
будут отличаться от скоростей в точке М на величину
υ−υ=υ
*
d
, которая и определяет деформированное состояние в
окрестности точки М:
)(d
z
*
zy
*
yx
*
x
,, υ−υυ−υυ−υ=υ
.
При переходе от точки М к точке М
*
эти величины будут изменяться в
соответствии с формулами:
z
z
y
y
x
x
iii
i
dddd
∂
υ
∂
+
∂
υ
∂
+
∂
υ
∂
=υ (9.1)
В краткой записи:
j
j,ii
dd
υ
=
υ
(9.2)
где dυ
i
- абсолютный дифференциал векторного поля
υ
;
υ
i,j
- абсолютная производная векторного поля скорости перемещения.
46
Матрица коэффициентов (υ
i,j
) в выражении (9.2) представляет тензор
второго ранга – тензор абсолютной производной векторного поля скорости
перемещения и имеет вид:
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
∂
υ∂
=υ
zyx
zyx
zyx
zzz
yyy
xxx
j,i
(9.3)
Тензор абсолютной производной, как любой тензор, можно
представить в виде суммы симметричной (с матрицей T
ξ
) и
кососимметричной (с матрицей T
ω
) частей. В символической записи они
будут иметь вид:
)(
2
1
i,jj,i
T υ+υ=
ξ
;
)(
2
1
i,jj,i
T υ−υ=
ω
(9.4)
В развернутом виде тензор T
ξ
записывают в виде матрицы:
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
+
∂
υ∂
∂
υ∂
=
ξ
zzyzx
yzyyx
xzxyx
T
z
y
zxz
z
yy
x
y
zx
y
xx
2
1
2
1
2
1
2
1
2
1
2
1
,
и называют тензором скорости деформации.

47
Тензор T
ω
, характеризуемый матрицей:
∂
υ∂
−
∂
υ∂
−
∂
υ∂
−
∂
υ∂
−
∂
υ∂
−
∂
υ∂
∂
υ∂
−
∂
υ∂
−
∂
υ∂
−
∂
υ∂
∂
υ∂
−
∂
υ∂
=
ω
0
2
1
2
1
2
1
0
2
1
2
1
2
1
0
yzxz
yzxy
xzxy
T
z
y
z
x
z
yy
x
zx
y
x
,
называется тензором вращения (поворота).
Контрольные вопросы
1. Дайте определение тензора абсолютной производной векторного поля
скорости.
2. Как называется симметричная и кососимметричная части тензора
абсолютной производной векторного поля скорости.
3. Какой имеют механический смысл и как называются компоненты тензора
скорости деформации?
4. Какова валентность тензора абсолютной производной векторного поля?
5. Как определяются компоненты тензора скорости деформации?
6. Как определяются компоненты тензора вращения?
ЛЕКЦИЯ 10
ТЕНЗОР СКОРОСТИ ДЕФОРМАЦИИ И ЕГО СВОЙСТВА.
СХЕМЫ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
План лекции:
1. Тензор скорости и его свойства
2. Инварианты тензора скорости деформации, приведение его к
диагональному виду.
3. Возможные схемы деформированного состояния.
4. Разложение тензора скорости на шаровой и девиатор скоростей
деформации.
5. Интенсивность скоростей деформации сдвига.

48
Рассмотрим подробней тензор скорости деформации. Его компоненты
обозначим ξ
ij
и представим в виде матрицы:
ξξξ
ξξξ
ξξξ
=
ξ
zzzyzx
yzyyyx
xzxyxx
Т
, (10.1)
а также в развернутой форме (с учетом, что ξ
ij
= ξ
ji
):
x
x
xx
∂
υ
∂
=ξ ;
y
y
yy
∂
υ
∂
=ξ
;
z
z
zz
∂
υ
∂
=ξ ;
∂
υ∂
+
∂
υ∂
=ξ=ξ
xy
y
x
yxxy
2
1
;
∂
υ∂
+
∂
υ∂
=ξ=ξ
xz
z
x
zxxz
2
1
; (10.2)
∂
υ∂
+
∂
υ∂
=ξ=ξ
zy
y
z
zyyz
2
1
.
Уравнения (10.2) получили название кинематических.
Компоненты тензора скорости деформации, стоящие на главной
диагонали матрицы (10.1) ξ
xx
, ξ
yy
, ξ
zz
, называют скоростями относительного
удлинения в направлении осей соответственно x, y, z, а компоненты ξ
xy
, ξ
yz
, ξ
xz
на остальных местах матрицы – половинными значениями скоростей сдвига
в плоскостях соответственно x0y, y0z, x0z.
Тензор скорости деформации, как любой симметричный тензор второго
ранга, имеет три взаимно-перпендикулярных собственных вектора и три
собственных значения, которые называют соответственно направлениями
главных скоростей относительных удлинений и главными скоростями
относительных удлинений ξ
11
, ξ
22
, ξ
33
.
Порядок определения главных скоростей изложен в лекции 6. По
матрице (10.1) составляют инварианты:
(
)
zzyyxx
TI
ξ
+
ξ
+
ξ
=
ξ1
;
( )
zzzx
xzxx
zzzy
yzyy
yyyx
xyxx
TI
ξξ
ξξ
+
ξξ
ξξ
+
ξξ
ξξ
=
ξ2
; (10.3 а)
49
( )
zzzyzx
yzyyyx
xzxyxx
TI
ξξξ
ξξξ
ξξξ
=
ξ3
.
которые являются коэффициентами характеристического уравнения:
λ
3
– I
1
λ
2
+ I
2
λ – I
3
= 0
Максимальный (в алгебраическом смысле) из корней λ этого
кубического уравнения будет ξ
11
, минимальный ξ
33
, средний ξ
22
.
Из-за ограничения, накладываемого условием несжимаемости
деформируемого материала
ξ
11
+ ξ
22
+ ξ
33
= 0,
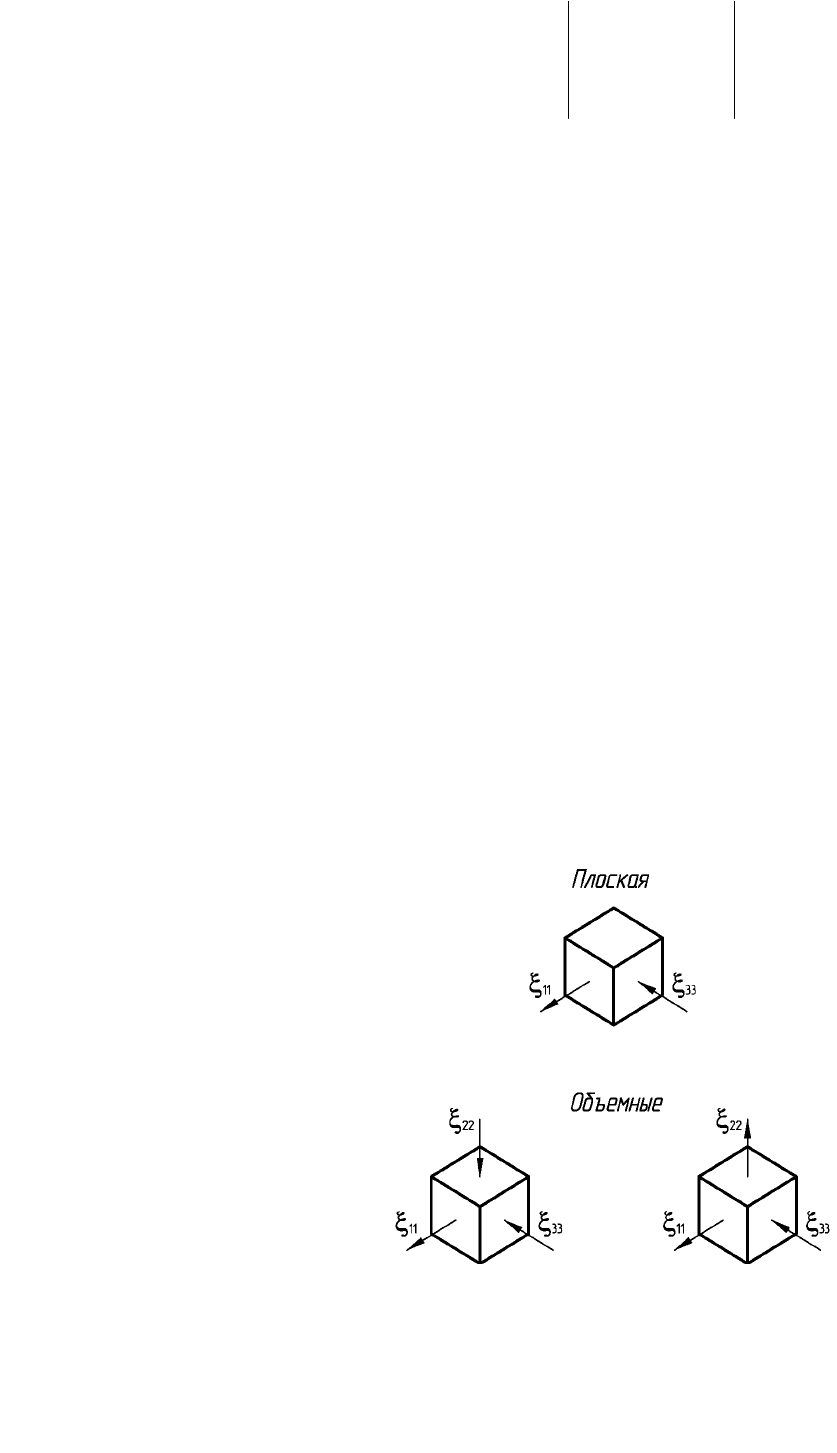
существуют только три возможных схемы главных деформаций (рис. 10.1 а)
схема с одной деформацией положительной и двумя другими
отрицательными, то есть растяжение, с одной отрицательной и двумя
положительными, то есть сжатие (рис. 10.1 б), и, наконец, с одной
деформацией, равной нулю, и двумя другими, равными по абсолютной
величине и противоположными по знаку (плоское деформированное
состояние – сдвиг) (рис. 10.1 в).
Рис. 10.1 Возможные схемы главных деформаций
Рис. 10.1 Схемы главных деформаций
б в
а

50
Первый инвариант тензора скорости деформации характеризует
скорость относительного изменения объема:
ξ = I
1
(T
ξ
) = ξ
xx
+ ξ
yy
+ ξ
zz
= ξ
11
+ ξ
22
+ ξ
33
. (10.4)
Выделим из тензора скорости деформации новый тензор, который
связан только с изменением формы тела и называется девиатором скорости
деформации:
ETD ξ−=
ξξ
3
1
, (10.5)
где Е – матрица составляющих единичного тензора.
Компоненты девиатора скорости деформации D
ξ
можно представить в
виде:
ijijij
e ξδ−ξ=
3
1
,
или, более подробно,
ξ−ξξξ
ξξ−ξξ
ξξξ−ξ
=
ξ
3
1
3
1
3
1
zzzyzx
yzyyyx
xzxyxx
D (10.6)
Тензор, определенный матрицей ( Еξ
3
1
), называют шаровым. Он
характеризует изменение объема.
Если материал несжимаем (это довольно распространенная гипотеза в
механике сплошных сред), то ξ = 0 и D
ξ
= T
ξ
, т.е. компоненты девиатора и
тензора скорости деформации совпадают: e
ij
= ξ
ij
.
