Загиров Н.Н. Теория обработки металлов давлением
Подождите немного. Документ загружается.


191
Решая совместно уравнения (38.2) и (38.3), при условии действия на
поверхности контакта закона трения по Амонтону-Кулону τ = µσ
n
, имеем:
∫
=
∫
ϕ
µσ
−τ
σ
h
h
n
S
n
d
tg
2
d
,
а после интегрирования
µ
ϕ
τ+⋅=σ
ϕµ−
tg
2
tg
S
/
n
hC
где С – постоянная интегрирования.
Используя граничное условие
Shhn
τ=σ
=
2
0
, исключая тем самым с из
формулы, в результате получим:
−
+
ϕ
µ
µ
ϕ
=
τ
σ
ϕµ
11
tg
tg
2
tg
0
/
S
n
h
h
.
Для процесса волочения листа (рис. 38.3) при условии, что в процессе
деформирования ширина листа b не меняется, уравнение равновесия
выделенного элемента запишется в виде:
0
cos
d
sin2
cos
d
cos2)tgd2)(d( =
α
ασ−
α
ατ−α⋅−σ+σ+σ−=Σ b
x
b
x
bxhhbF
nxxxxxxx
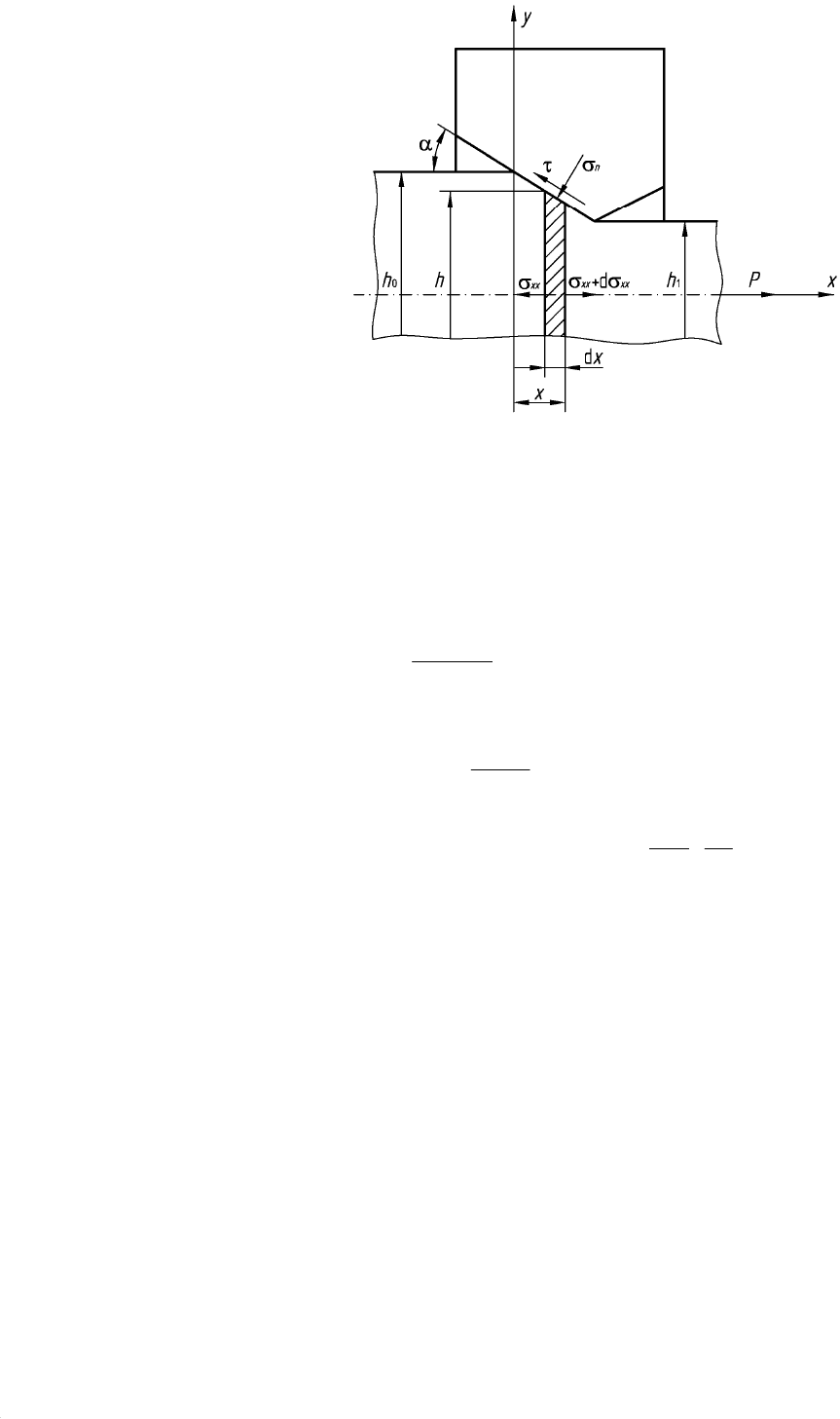
192
Рис. 38.3. Схема процесса волочения листа
После раскрытия скобок, ряда преобразований и удаления бесконечно малых
величин второго порядка малости уравнение примет вид:
( )
02tg2
d
d
=τ−σ+σα−=
⋅
σ
nxx
xx
x
h
или с учетом того, что
ϕ
=
tg
2d
d
/h
x ,
h
h
nxxxx
d
tg
d
α
τ
+σ+σ=σ . (38.4)
Условие пластичности для рассматриваемого случая можно записать в виде:
σ
xx
+ σ
n
= τ
S
,
а после деформирования по переменной х:
dσ
xx
= - dσ
n
. (38.5)
Решая совместно уравнения (38.4) и (38.5), получим:
- для случая действия на контактной поверхности закона трения по Зибелю
τ=ψτ
S
:

193
∫
α
ψτ
+τ=
∫
σ−
σ
1
0
0
d
tg
2d
h
h
S
S
n
n
h
h
,
а после интегрирования
1
0
ln
tg
1
2 h
h
S
n
α
ψ
+=
τ
σ
;
- для случая действия на контактной поверхности закона трения по
Амонтону-Кулону τ = µσ
n
:
∫ ∫
α
µ
=
σ+
µ
α⋅τ
σ
τ
σ−τ
s
/
ns
h
h
n
S
n
h
h
2
1
0
d
tg
tg
d
,
а после интегрирования
−
µ
α
+=
τ
σ
αµ tg
0
1
1
tg
1
2
/
S
n
h
h
.
Контрольные вопросы
1. Что рассматривает инженерный метод?
2. Алгоритм решения задач с помощью инженерного метода.
3. Как рассчитывается полное усилие осадки прямоугольного
параллелепипеда?
4. Какой закон трения принимается в случае осадки прямоугольного
параллелепипеда?
5. Как запишется условие пластичности для случая плоской прокатки?
6. Как запишется условие пластичности для случая волочения листа?
7. Какой закон трения принимается в случае плоской прокатки?
8. Какой закон трения принимается в случае волочения листа?
194
ЛЕКЦИЯ 39
ОСОБЕННОСТИ РЕАЛИЗАЦИИ ИНЖЕНЕРНОГО МЕТОДА ПРИ
РЕШЕНИИ ЗАДАЧ В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ
План лекции:
1. Особенности реализации инженерного метода при решении задач в
цилиндрической системе координат.
2. Примеры решения задач.
При решении задач обработки металлов давление часто встречаются
случаи, когда деформируется тело вращения, например, цилиндр, под
действием распределенной нагрузки, приложенной симметрично его оси.
Такое напряженное состояние называется осесимметричным, и оно является
частным случаем объемного напряженного состояния.
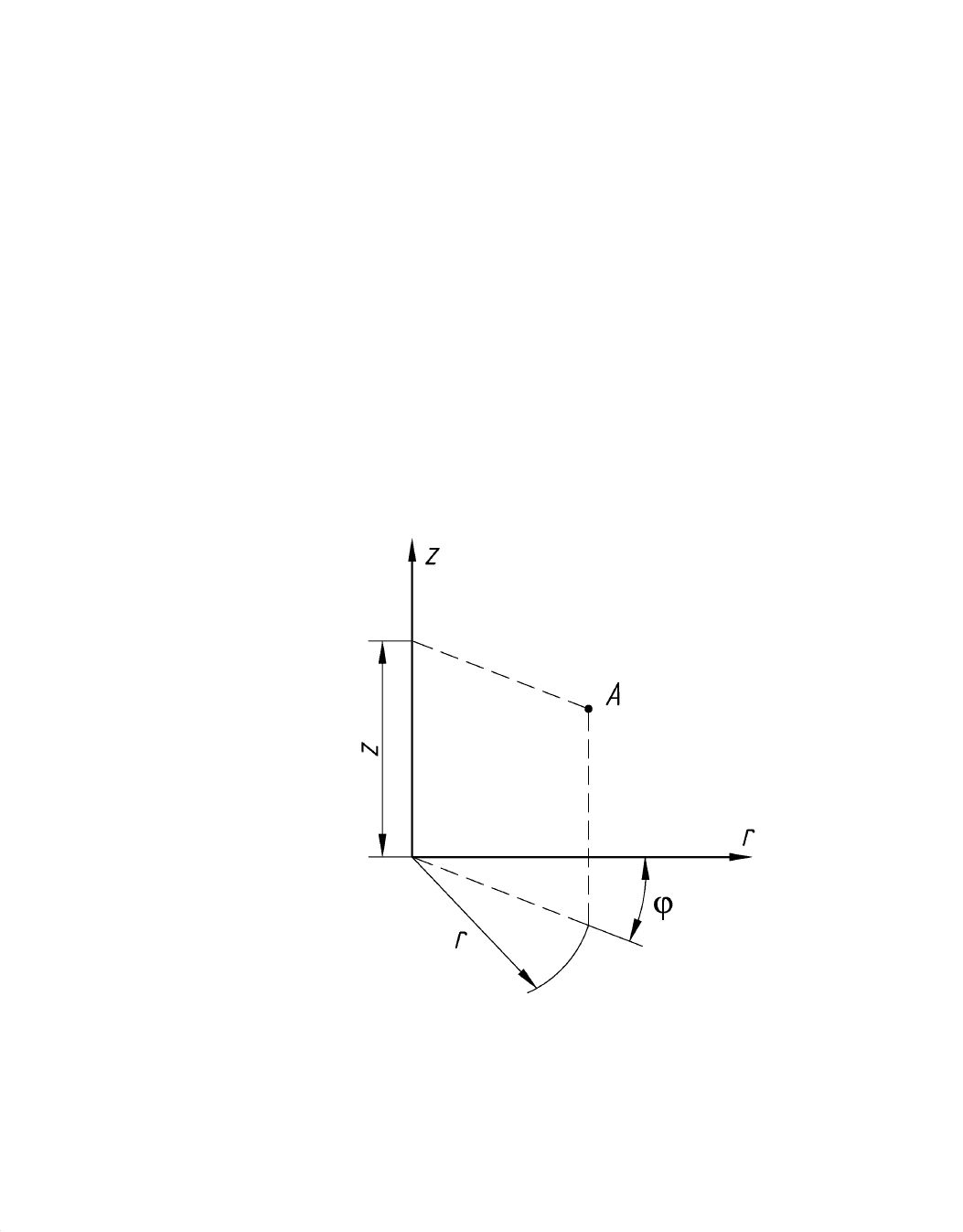
Решение осесимметричных задач удобнее вести в цилиндрических
координатах взамен прямоугольных декартовых. В цилиндрических
координатах положение точки определяется радиус-вектором r, и апликатой
z, определяющей расстояние точки от плоскости rϕ (рис. 39.1).
Рис. 39.1. Цилиндрические координаты
195
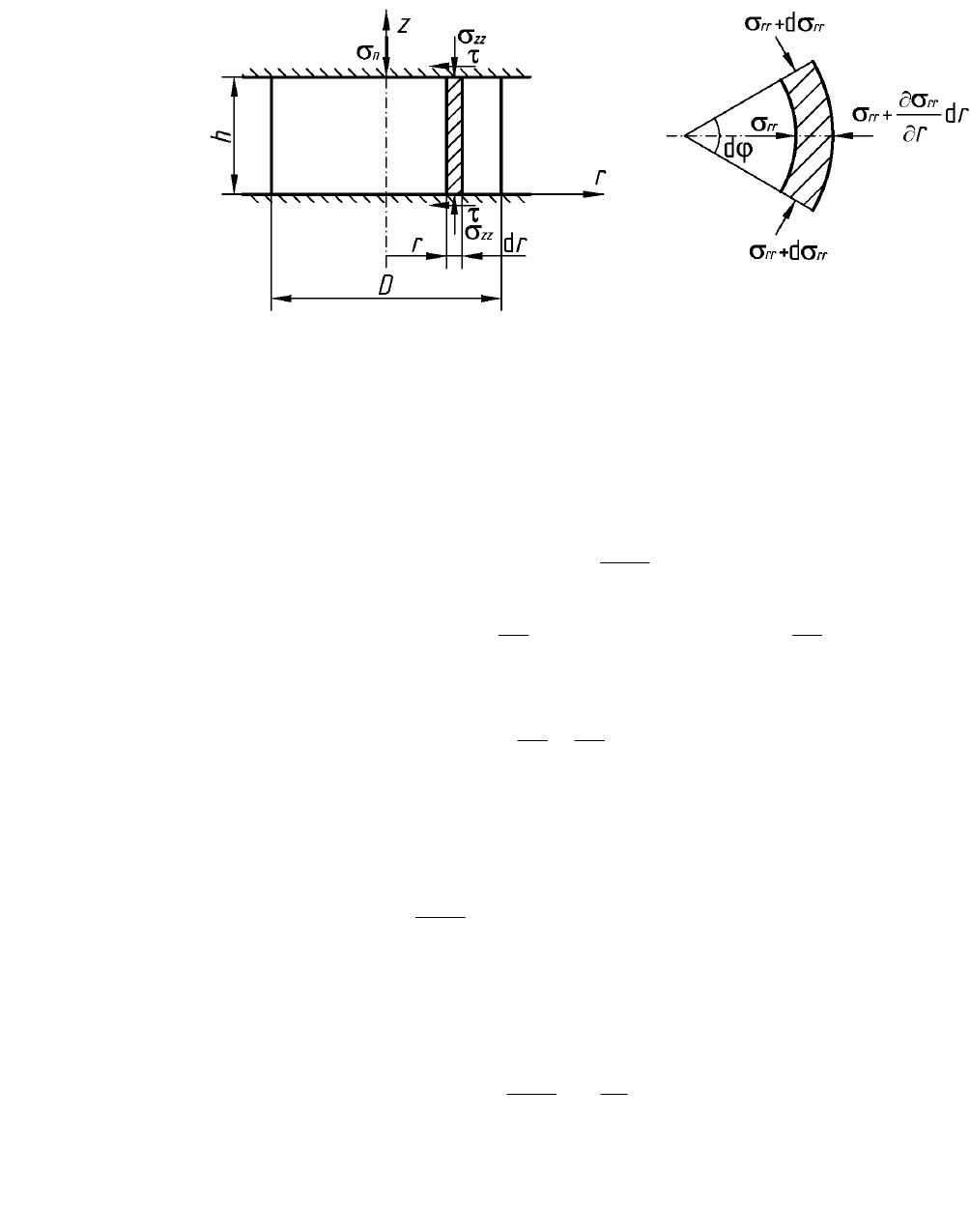
Форма элемента и напряжения в координатных плоскостях при
решении задачи инженерным методом в цилиндрической системе координат
показаны на рис. 39.2 применительно к процессу осадки цилиндрической
заготовки.
Рис. 39.2. Схема процесса осадки цилиндрической заготовки
Составляем уравнение равновесия выделенного элемента,
спроецировав все действующие на него силы на ось r:
( )
( ) ( )
[ ]
0
2
d
d2d
2
d
sind2
dddd
2
2
=
ϕ
−+τ−⋅⋅
ϕ
σ+σ+
+⋅ϕ+
∂
σ
∂
+σ−⋅ϕ⋅⋅σ=Σ
rrrhr
hrrr
r
hrF
rrrr
rr
rrrrr
.
Если принять, что
2
d
2
d
ϕ
≈
ϕ
sin
, раскрыть скобки и пренебречь
бесконечно малыми величинами больших порядков малости, чем drdϕ, то
уравнение существенно упростится и примет вид:
0dd2dd =ϕ⋅⋅⋅τ−⋅⋅ϕ⋅
∂
σ
∂
− rrhrr
r
rr
,
а после сокращения на множитель r⋅ dr ⋅ dϕ –
h
r
rr
τ
−=
∂
σ
∂
2
. (39.1)
196
Условие пластичности в случае деформирования осесимметричной заготовки
можно записать в виде
σ
zz
- σ
rr
= σ
S
,
а после дифференцирования по переменной r (с учетом, что dσ
zz
= dσ
n
):
dσ
n
= dσ
rr
. (39.2)
Решая совместно уравнения (39.1) и (39.2) , при условии действия на
поверхности контакта закона трения по Зибелю τ = ψτ
S
, имеем:
∫
+
ψτ
−=
ψτ
−=σ Cr
h
r
h
SS
n
2
d
2
.
Постоянная интегрирования С находится, исходя из допущения 0
2
=σ
= /Drrr
и вытекающего из условия пластичности соотношения
S/Drn
σ=σ
= 2
и
составляет:
h
D
C
SS
ψτ+σ= .
Тогда величина безразмерного показателя напряженного состояния составит
( )
rD
h
S
n
2
3
1 −
ψ
+=
σ
σ
.
Для случая действия на контакте закона трения по Амонтону-Кулону τ = µσ
n
имеем:
∫ ∫
µ
−=
σ
σ
r
h
n
n
d
2
d
,
а после интегрирования
197
Cr
h
n
+
µ
−=σ
2
ln .
С учетом граничного условия
S/Drn
σ=σ
= 2
после ряда математических
преобразований получим формулу для нахождения показателя напряженного
состояния для данного случая:
( )
−
µ
=
σ
σ
rD
h
S
n
2exp .
Цилиндрическая система координат используется и при рассмотрении
процесса волочения проволоки (рис. 39.3).
Рис. 39.3. Схема процесса волочения проволоки
Уравнение равновесия выделенного элемента в этом случае запишется
следующим образом:
(
)
(
)
( ) ( )
0d
cos
d
sind
cos
d
cos
dd
2
2
=−+
α
π⋅α⋅σ−−+
α
π⋅α⋅τ−
−−πσ+σ+πσ−=Σ
rrr
z
rrr
z
rrrF
n
zzzzzzz
.
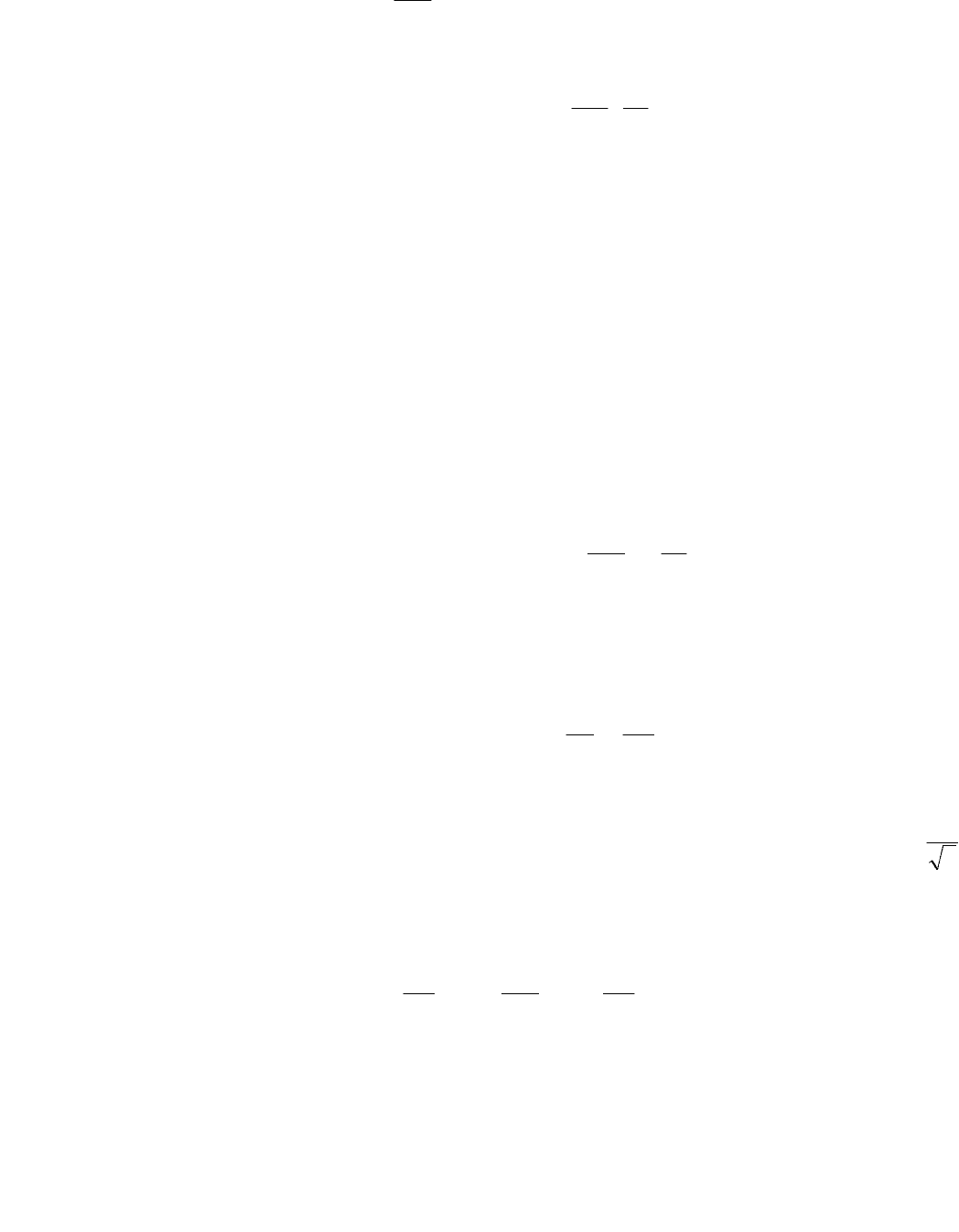
198
После раскрытия скобок, ряда преобразований и удаления бесконечно малых
величин высших порядков малости уравнение с учетом того, что r=R
0
–z ⋅ tgα,
а следовательно
α
−=
tg
d
d
r
z
, примет вид:
r
r
tg
nzzzz
d
2d
α
τ
+σ+σ−=σ
. (39.3)
Условие пластичности для рассматриваемого случая можно записать в виде:
σ
zz
- σ
n
= σ
S
,
а после дифференцирования
dσ
zz
= dσ
n
. (39.4)
Решая совместно уравнения (39.3) и (39.4), получим:
∫∫
α
τ
+σ−=σ
1
0
d
tg
2d
R
R
Sn
r
r
,
а после интегрирования:
(
)
2
1
2
0
tg
ln
R
R
Sn
α
τ
+σ=σ
.
Для случая действия на контакте закона трения по Зибелю
3
S
S
σ
ψ=ψτ=τ
имеем:
−
µ
α
+=
σ
σ
αµ tg
2
1
2
0
1
tg
1
/
S
n
R
R
.

199
В случае же действия на контакте закона трения по Амонтону-Кулону
τ=µσ
n
безразмерный показатель напряженного состояния будет равняться:
−
µ
α
+=
σ
σ
αµ tg
2
1
2
0
1
tg
1
/
S
n
R
R
.
Контрольные вопросы
1. Чем определяется положение точки в цилиндрических координатах?
2. Как запишется условие пластичности в случае деформирования
осесимметричной заготовки?
3. Как запишется условие пластичности в случае волочения?
4. Как определяется показатель
S
n
σ
σ
в случае деформирования
осесимметричной заготовки?
5. Как определяется показатель
S
n
σ
σ
в случае волочения?
6. Как составляется уравнение равновесия в случае деформирования
осесимметричной заготовки?
7. Как составляется уравнение равновесия в случае волочения?
ЛЕКЦИЯ 40
СУЩНОСТЬ ЭНЕРГЕТИЧЕСКОГО МЕТОДА И ПРИМЕР
ЕГО ИСПОЛЬЗОВАНИЯ В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
План лекции:
1. Сущность энергетического метода (метода баланса мощностей).
2. Общий вид уравнения баланса мощностей и определение отдельных его
составляющих.
3. Пример решения задачи в декартовой системе координат
Базовым положением энергетического метода (метода баланса
мощностей) является следующее выражение: мощность, подводимая к
деформируемому телу со стороны инструмента N, затрачивается
непосредственно на формоизменение (деформацию) обрабатываемого тела
N
д
и на преодоление сил трения на контактных поверхностях N
тр
, т.е.

200
N = N
д
+ N
тр
Это равенство называется уравнением баланса мощностей и выражает
закон сохранения энергии при пластическом течении.
Неизвестные или криволинейные границы между очагом деформации и
внешними зонами заготовки часто условно заменяют плоскостями, допуская
возможность среза металла по условной геометрической границе очага
деформации. Иногда для упрощения задачи весь очаг делят на зоны с
поверхностями среза между ними. Тогда в правую часть уравнения
добавляется мощность сил среза N
ср
, и уравнение баланса мощностей
запишется в виде
N = N
д
+ N
тр
+ N
ср
.
Мощность, подводимая к деформируемому телу со стороны
инструмента, в общем случае выражается формулой
N = P ⋅ ϑ,
где Р - усилие деформирования;
ϑ - скорость перемещения рабочего органа машины.
Мощность, необходимая для деформации материала заготовки,
размеры которой известны, рассчитывается по формуле:
∫∫∫
=
V
VTHN d
Д
,
где Т - интенсивность касательных напряжений;
Н - интенсивность скоростей деформации сдвига;
V - объем деформируемого тела.
