Загиров Н.Н. Теория обработки металлов давлением

Подождите немного. Документ загружается.

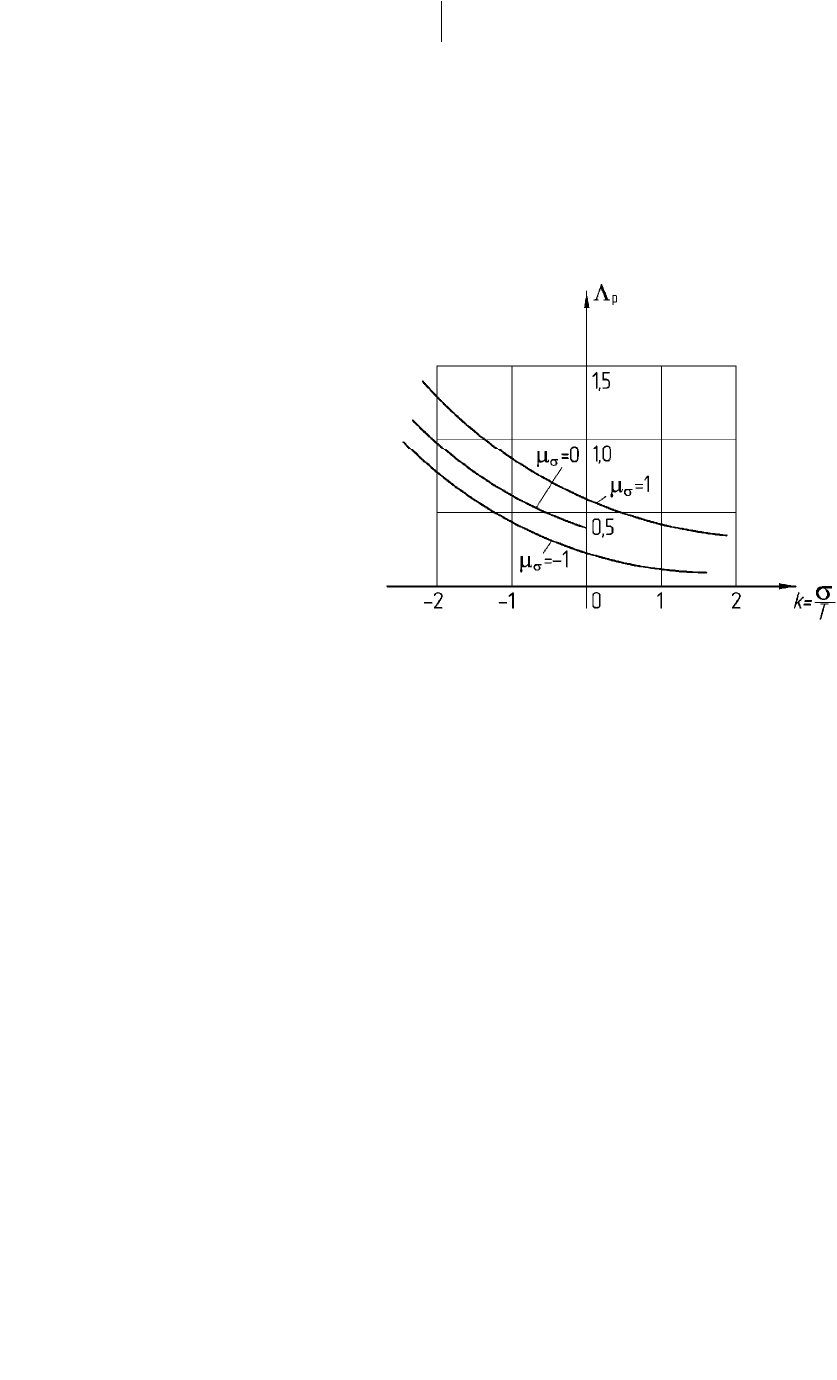
171

Аналогичные рассуждения можно провести и для испытаний на сжатие

в камере высокого давления, по результатам которых определяют

зависимость

(

)

1PP =

λ=λ k .

Обобщим все данные, приведенные выше. Графическое изображение

функциональной зависимости λ

= λ

(k, µ

) называют диаграммой

пластичности. На рис. 35.2 показан характерный вид диаграммы

пластичности, свойственный большинству обрабатываемых давлением

металлов и сплавов.

Рис. 35.2. Диаграмма пластичности

Анализируя графики (рис. 35.2), можно сделать следующие выводы:

1. Зависимость λ

= λ

(k) при µ

= const всегда убывающая. Она показывает,

что рост сжимающих напряжений всегда повышает пластичность металла

при прочих равных условиях.

2. Однозначной зависимости λ

от µ

при k = const нет. Одни металлы с

ростом µ

повышают пластичность, другие нет, третьим свойственно

повышение λ

с ростом µ

лишь в условиях существенных сжимающих

напряжений, а при больших значениях k эта зависимость обратная. Другими

словами, последовательность расположения линий на диаграмме

пластичности для тех или иных значений µ

может быть произвольной.

3. Относительная пластичность, определенная при каких-то показателях

напряженного состояния, не может характеризовать относительную

пластичность этого же металла в условиях с существенно отличным

напряженным состоянием, т.е. с иными показателями k и µ

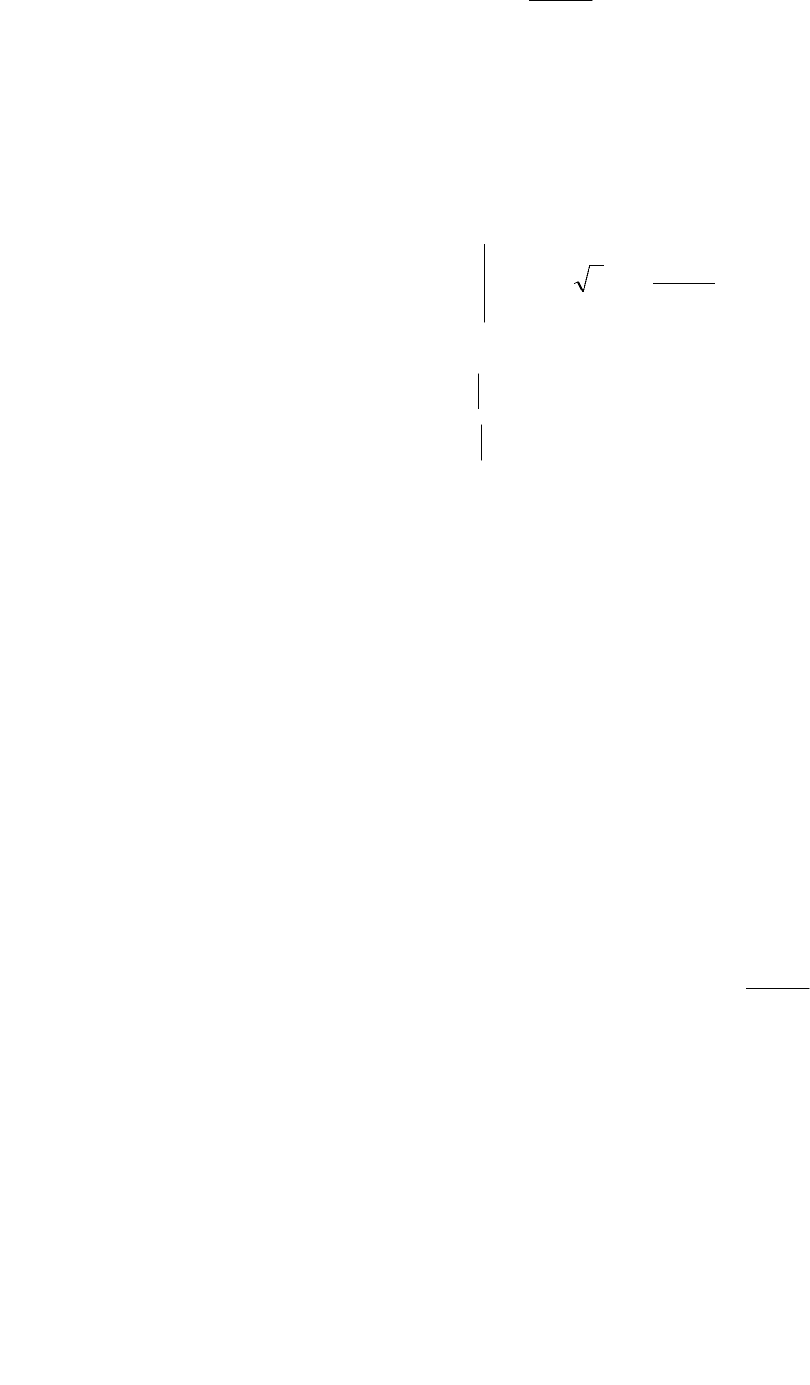
172

Например, служащая в качестве показателя пластичности величина

относительного удлинения %

100

⋅

−

=δ свидетельствует о пластичности

металла лишь при k = 0,58 и µ

= – 1 (одна точка на диаграмме

пластичности). Правда, значение δ позволяет сделать в некоторых случаях

оценку λ

при других значениях показателя k.

Нетрудно показать, что













⋅=λ

−=

100%

ln3

580P ,k

Тогда при k > 0,58

580PP ,k=

λ<λ , а

при k < 0,58

580PP ,k=

λ>λ (при одинаковом µ

= – 1).

4. По-видимому, существуют критические значения показателей

напряженного состояния для каждого сплава: при одних k и µ

→0 и

происходит переход из пластического состояния в хрупкое, а при других

→∞ - металл переходит в состояние неограниченной пластичности.

Контрольные вопросы

1. Как давление жидкости изменяет главные напряжения при испытании на

кручение?

2. Как определяют степень деформации сдвига в момент разрушения образца

при испытании на кручение?

3. Графическое изображение какой функциональной зависимости называют

диаграммой пластичности?

4. При каких k и µ

относительного удлинения %

100

⋅

−

=δ

свидетельствует о пластичности металла?

5. Как влияет рост сжимающих напряжений на пластичность металла?

173

ЛЕКЦИЯ 36

ВОССТАНОВЛЕНИЕ ПЛАСТИЧНОСТИ ПРИ ОТЖИГЕ

ХОЛОДНОДЕФОРМИРОВАННЫХ ИЗДЕЛИЙ.

ПЛАСТИЧНОСТЬ МЕТАЛЛОВ ПРИ ГОРЯЧЕЙ ОБРАБОТКЕ

План лекции:

1. Модель восстановления запаса пластичности при отжиге холодно-

деформированных изделий.

2. Диаграмма, характеризующая стадии накопления поврежденности металла

при деформации и возможности ее уменьшения при последующей

термообработке.

3. Пластичность металлов при горячей обработке.

4. Понятие сверхпластичности металла.

Холодную деформацию листа, труб, проволоки и т.п. часто

осуществляют в несколько этапов, и это сопровождается промежуточными и

окончательным отжигами. При отжиге идут процессы разупрочнения

металла и восстановления его пластических свойств, причем природа этих

процессов разная. В основе восстановления пластичности лежат

диффузионные процессы переноса вещества в поры и микротрещины.

Дадим математическое описание того, как происходит восстановление

запаса пластичности при отжиге. Для решения этой задачи может быть

использована следующая методика.

Эксперимент осуществляют с металлом, пластичность которого

=λ

(k, µ

) достаточно изучена. Образцы опытной партии подвергают

пластической деформации на различную степень использования запаса

пластичности ψ

, но не до разрыва. Затем все образцы подвергают отжигу по

избранным температуре Θ и времени выдержки t. При отжиге произойдет

восстановление пластичности образцов на величину ∆ψ. После отжига все

образцы вновь подвергают пластической деформации, но уже до разрушения.

При этом фиксируют λ

и вычисляют ψ

= λ

/ λ

. Вторая пластическая

деформация играет вспомогательную роль для определения ∆ψ.

В итоге имеем (деформация в опытах близка к монотонной, образцы

вторым деформированием доведены до разрушения)

ψ = ψ

- ∆ψ + ψ

= 1,

174

а это позволяет найти

∆ψ = – 1 + ψ

+ ψ

. (36.1)

Результаты экспериментов по определению восстановления запаса

пластичности ∆ψ при отжиге, проведенных для некоторых сталей и сплавов,

показали, что восстановление пластичности в значительной степени зависит

от ψ

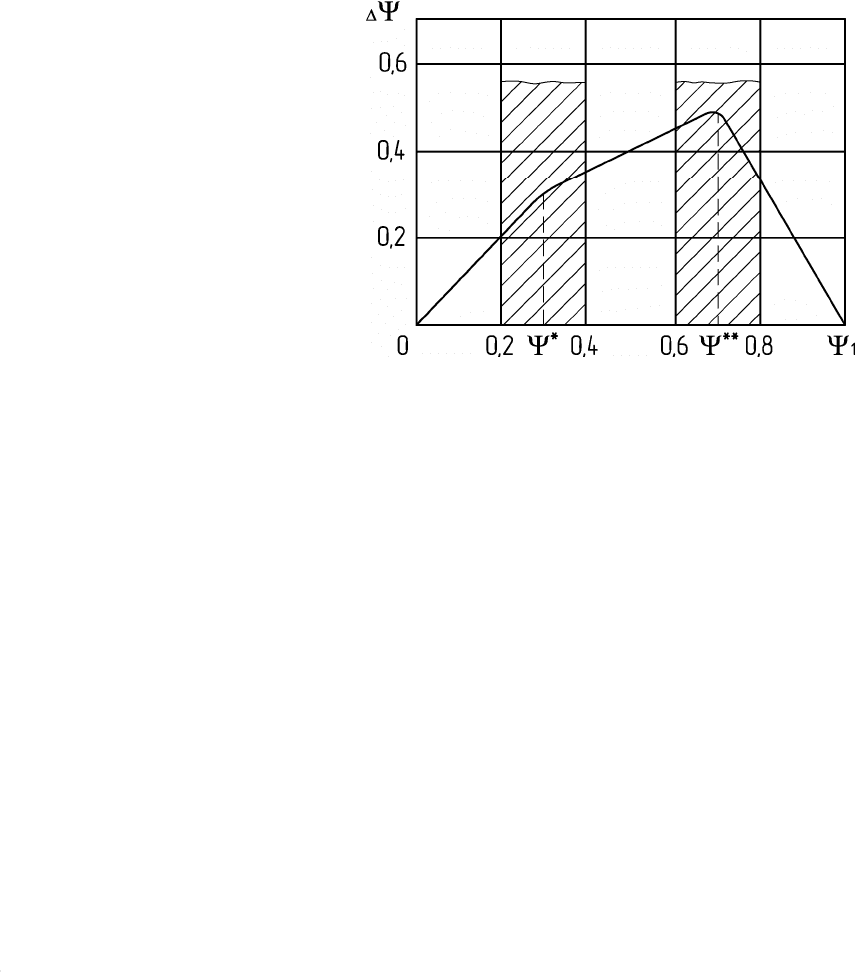
, т.е. от величины деформации λ до проведения отжига. Диаграмма

(рис.36.1) характеризует стадии накопления поврежденности при

деформации и возможности ее уменьшения при последующей термической

обработке. Она имеет три характерных участка: [0… ψ*], [ψ*…ψ**],

[ψ**…1].

Рис. 36.1. Диаграмма, характеризующая стадии накопления поврежденности

при деформации и возможности ее уменьшения при последующей термообработке

Термическая обработка после пластической деформации с величиной ψ

≤ ψ* полностью устраняет накопленную за процесс деформации

поврежденность микродефектами (∆ψ = ψ

Условие ψ* ≤ ψ ≤ ψ** соответствует образованию в металле

энергетически устойчивых микропор, не залечиваемых полностью при

отжиге по принятому режиму (∆ψ < ψ

После деформации с ψ > ψ** возможность устранения поврежденности

микродефектами при отжиге уменьшается, а при достижении ψ = 1

происходит макроразрушение металла.

175

Штриховкой показаны области изменения величин ψ* и ψ** для

различных металлов.

Наличие микродефектов сплошности металла в некоторых изделиях не

всегда приводит к снижению эксплуатационных характеристик. Поэтому при

проектировании технологии ОМД следует применять дифференцированный

подход к назначению деформаций и отжигов и учитывать условия

эксплуатации изделий.

Кроме того, известно, что микроскопические нарушения сплошности

могут самопроизвольно развиваться после прекращения пластической

деформации. Это происходит, если материал получил при обработке высокое

значение ψ и если в металле имеют место значительные остаточные

напряжения.

Система ограничений по величине ψ может быть такой:

1. < 1 – допускается для изделий, не несущих значительных нагрузок;

2. ≤ ψ** = 0,6…0,8 – для большинства выпускаемых изделий, у которых

существуют ограничения по нижнему пределу прочности, вязкости и

долговечности;

3. ≤ψ* = 0,2…0,4 – для изделий, работающих в особенно неблагоприятных

условиях.

Последнее неравенство можно охарактеризовать как условие

получения продукции без микродефектов сплошности деформационного

происхождения.

Другой задачей, которую приходится решать при проектировании

технологии холодной деформации с отжигами, является выбор режима

термообработки из условия наиболее полного восстановления запаса

пластичности. Для этого следует рассмотреть изменение ψ во времени при

некоторой температуре термообработки, если при t = 0, ψ = ψ

На рис. 36.2 показана такая временная зависимость для стали марки 20

и температуры отжига 600 °С.

176

Рис. 36.2. Изменение степени использования запаса пластичности во времени

Самая нижняя кривая при ψ

= 0 означает, что отжиг заготовки для

деформации, например, горячекатаных труб, может привести к повышению

ее пластичности.

Если ψ

≤ 0,2 ≈ ψ*, то пластичность в течение 2 ч восстановится

полностью. Если ψ

>ψ* (0,6…0,7) – пластичность в рассмотренном

интервале не восстанавливается.

Кривые ψ = ψ(t) имеют три характерных участка: АВ –

экспоненциально быстрого восстановления пластичности; ВС –

значительного замедления процесса восстановления пластичности и даже его

остановки; CD – дальнейшего восстановления.

Рассмотрение подобных данных при других температурах отжига

позволяет избрать рациональное время отжига t и его температуру Θ.

Расчет деформируемости металлов при температурах выше

температуры рекристаллизации, когда процессы возникновения субмикро- и

микродефектов от пластического течения сопровождаются их залечиванием

диффузионным путем и перекристаллизацией, несколько сложней. При этом

в условии деформирования без разрушения следует учесть торможение

разрыхления с помощью функции Е(t), которая названа функцией

наследственности.

Тогда формула (34.2) запишется в виде

∫

=ψ

1d . (36.2)

177

Функция Е изменяется в пределах 0 < E(t )≤ 1. Для холодной

деформации Е(t) = 1; чем выше температура, тем меньше ее значение.

Для горячей обработки давлением до сих пор не удалось разработать

надежных методов количественной оценки показателя пластичности,

подобных, например, диаграммам пластичности для холодной деформации.

Это связано со сложностью проведения горячих испытаний в условиях

всестороннего сжатия жидкостью высокого давления.

В производственной практике получили распространение следующие

виды высокотемпературных испытаний:

1. на ударную вязкость, определяемую изломом надрезанного образца на

копре;

2. на кручение с оценкой числа оборотов до разрушения;

3. пластометрические испытания для определения максимальной степени

деформации при осадке и растяжении до появления трещин.

Неоднократно предпринимались попытки найти корреляцию, т.е.

вероятностную связь, между λ

и показателями указанных испытаний

образцов.

В целом зависимость пластичности λ

в горячем состоянии от показателя

напряженного состояния k качественно такая же, как и в холодном

состоянии. Инициирование сжимающих напряжений всегда приводит к

повышению пластичности деформируемого металла, а растягивающих – к ее

падению при прочих равных условиях. Зависимость λ

от µ

практически не

изучена.

При горячей деформации ряда сплавов в некоторых условиях

проявляется явление сверхпластичности, т.е. способность металлов и сплавов

равномерно удлиняться на сотни и тысячи процентов без разрушения.

Состояние сверхпластичности отличается малым сопротивлением

металлов пластической деформации и проявляется при:

1. наличии исходной ультрамелкозернистой структуры с равновесными

зернами размером не более 10 мкм;

2. температурах выше 0,4⋅Т

пл

, когда у металлов в процессе пластической

деформации происходят фазовые или иные структурные изменения;

3. скоростях деформации 10

-4

– 10

-2

-1

Преимущества обработки давлением в состоянии сверхпластичности –

повышенный ресурс пластичности и, следовательно, возможность

значительного формоизменения за одну операцию.

178

Недостатки – низкие скорости деформации и, следовательно,

невысокая производительность формоизменения.

Контрольные вопросы

1. Что лежит в основе восстановления пластичности при отжиге?

2. Система ограничений по величине степени использования запаса

пластичности ψ.

3. Охарактеризуйте участки кривой ψ = ψ(t).

4. Что учитывает и в каких пределах изменяется функция наследственности?

5. Какие виды высокотемпературных испытаний получили распространение в

производственной практике?

6. Что такое «явление сверхпластичности»?

7. В каких случаях проявляется явление сверхпластичности?

Раздел 10. Методы расчета формоизменения и энергосиловых

параметров при обработке металлов давлением

ЛЕКЦИЯ 37

ОБЩАЯ ПОСТАНОВКА АНАЛИТИЧЕСКИХ ЗАДАЧ В ТЕОРИИ ОМД.

МЕТОД, ОСНОВАННЫЙ НА РЕШЕНИИ УПРОЩЕННОЙ СИСТЕМЫ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ТЕОРИИ ПЛАСТИЧНОСТИ.

План лекции:

1. Общая постановка аналитических задач в теории ОМД.

2. Метод, основанный на решении упрощенной системы дифференциальных

уравнений теории пластичности.

3. Рассмотрение сущности метода на примере построения эпюры

нормальных напряжений при осадке прямоугольного параллелепипеда.

При разработке технологических процессов обработки давлением и

проектировании оборудования необходимо знать усилие, которое нужно

приложить к деформируемому телу для преодоления сопротивления металла

деформации и трения на поверхности контакта металла с инструментом.

179

Полное усилие определяет характеристику потребного оборудования –

усилие пресса, мощность двигателя прокатного стана, мощность главного

привода волочильного стана и т.п.

Аналитически усилие можно определить, зная нормальные и

касательные напряжения в каждой точке поверхности контакта металла с

инструментом, а также форму и размеры этой поверхности. Проецируя

составляющие нормальных и касательных напряжений на направление

действующего рабочего усилия по всей контактной поверхности, можно

определить полное усилие.

Результаты расчета представляют в виде формул, которые используют

для определения усилия деформации тел одинаковой формы, но других

размеров и при других значениях сопротивления деформации σ

коэффициента трения µ.

Этот метод заключается в решении упрощенной системы

дифференциальных уравнений теории пластичности, которые записывают в

форме (для объемного, осесимметричного, плоского напряженного

состояния, плоского деформированного состояния) и в координатах (прямо-

угольных, цилиндрических, сферических), отвечающих условиям

рассматриваемой конкретной задачи.

Произвольные постоянные определяют из граничных условий. Условия

трения принимают либо в форме закона Амантона-Кулона (29.2), либо закона

Зибеля (29.3).

Решение в принципе должно дать величину и распределение

напряжений по всему объему тела, т.е. значения напряжений как функций

координат точек тела, в том числе и лежащих на поверхности,

непосредственно воспринимающей активное усилие.

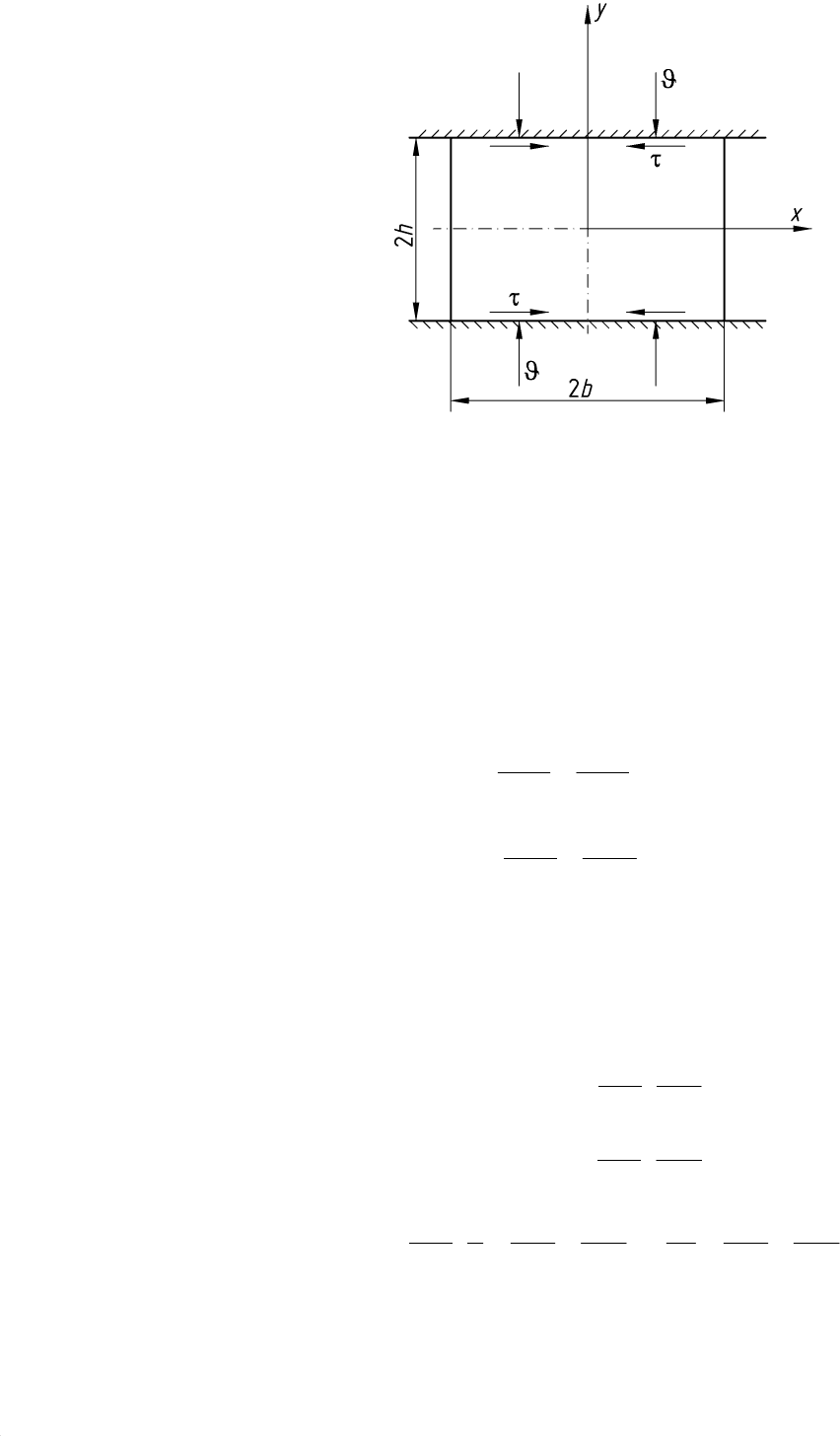
Сущность метода разберем на примере осадки прямоугольного

параллелепипеда бойками, перемещающимися навстречу друг другу с

постоянной скоростью ϑ (рис. 37.1). Задача – построить эпюру нормальных

напряжений, действующих на контактной поверхности.

Рассмотрим случай, когда длина параллелепипеда l намного больше его

ширины b (l >> b), поэтому, согласно закону наименьшего сопротивления,

течение металла в направлении оси z (вдоль длины l) отсутствует, т.е. в

наличии имеются только две составляющие вектора скорости перемещения -

иϑ

. Напряженное состояние характеризуется тремя составляющими - σ

, σ

180

Рис. 37.1. Схема процесса осадки прямоугольного параллелепипеда

В систему дифференциальных уравнений теории пластичности, как

известно, входит ряд уравнений. Запишем их применительно к условиям

нашей задачи.

1. Дифференциальные уравнения равновесия (с учетом того, что σ

= σ

)

упростятся:

∂

σ∂

; (37.1а)

∂

. (37.1б)

2. Физические уравнения связи напряжений и деформаций (при Т = τ

)

преобразуются к виду

∂

⋅

=σ−σ

;

∂

⋅

=σ−σ

;













∂

ϑ∂

∂

ϑ∂

⋅













∂

ϑ∂

∂

ϑ∂

⋅⋅

=σ

xyHxyH