Загиров Н.Н. Теория обработки металлов давлением
Подождите немного. Документ загружается.

141
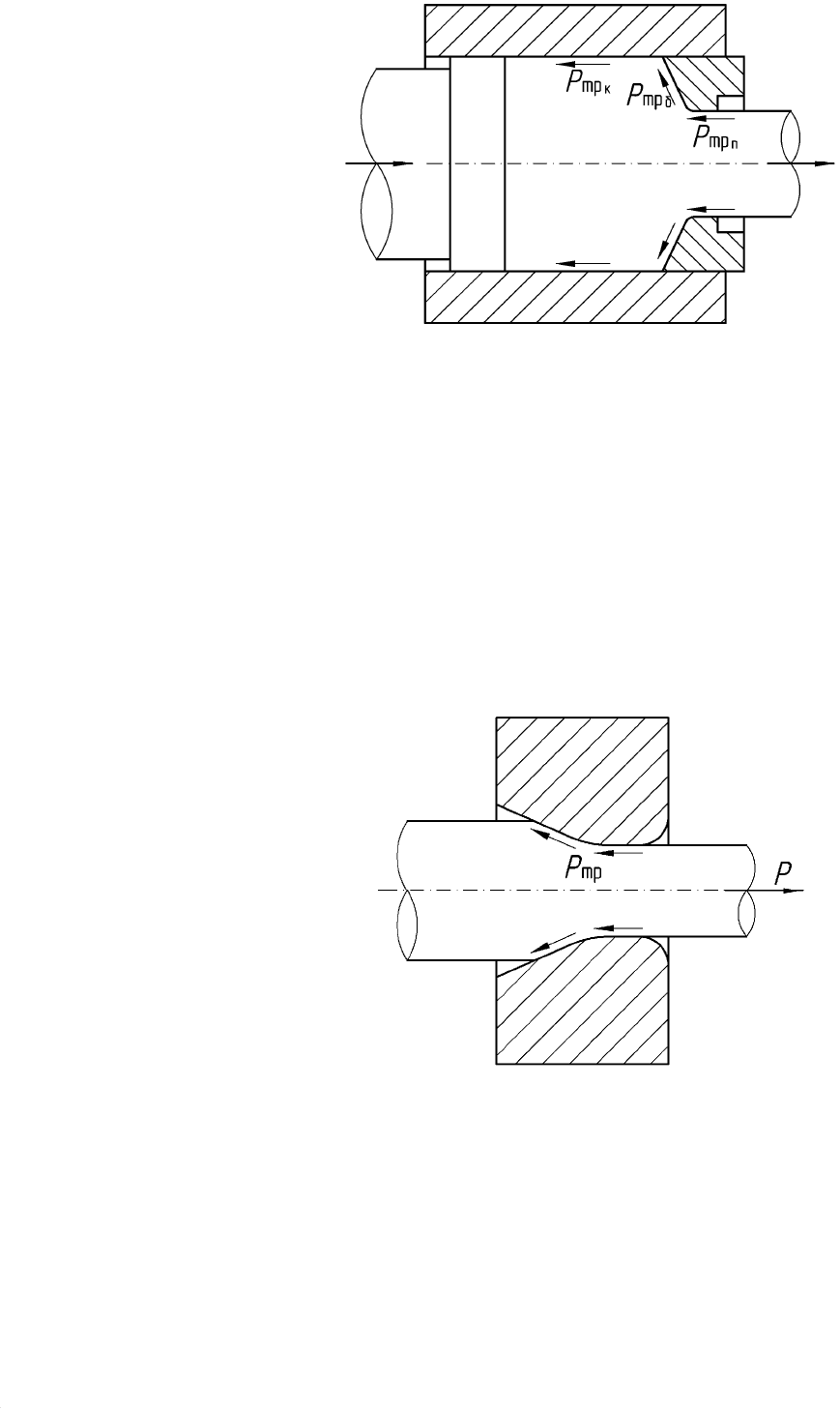
Рис. 28.2. Схема процесса прямого прессования прутка
Увеличение любой из составляющих сил трения Р
тр
приводит к
повышению общего усилия прессования.
3. Контактное трение снижает стойкость инструмента как в результате
непосредственного износа контактной поверхности, так и вследствие
дополнительного нагрева поверхности и увеличения напряжений в связи с
ростом деформирующего усилия. Этот фактор имеет первостепенное
значение при волочении проволоки (рис. 28.3).
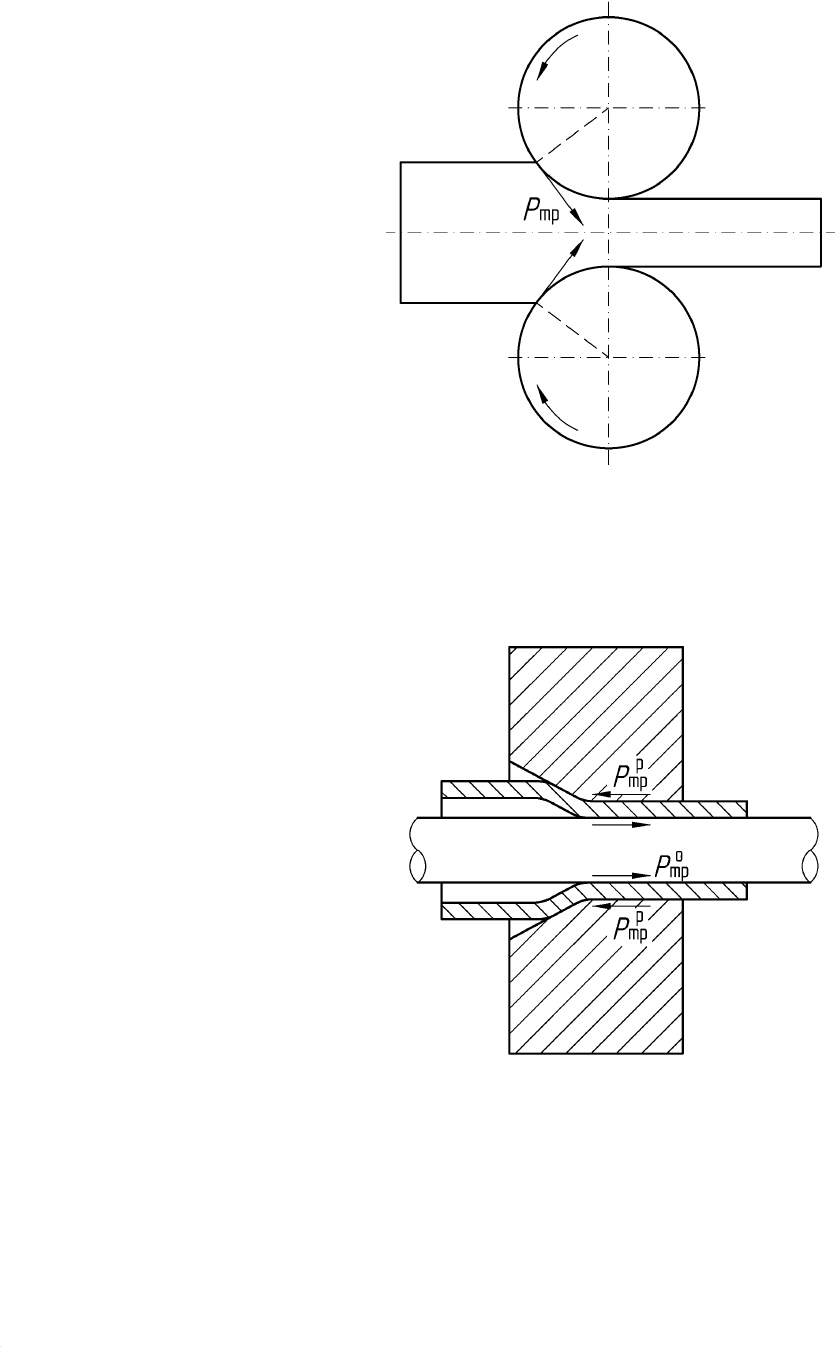
Рис. 28.3. Схема процесса волочения проволоки
В отдельных случаях силы трения необходимы и для их повышения
применяют специальные меры. Так, в момент захвата полосы валками при
прокатке (рис. 28.4), в месте контакта действуют силы трения, втягивающие
полосу в зазор между валками. Для их усиления применяют даже
142
специальные меры, например, наносят на поверхность валков насечки,
увеличивая тем самым их шероховатость.
Рис. 28.4. Схема процесса прокатки полосы
Активное действие сил трения наблюдается также при волочении трубы
на длинной подвижной оправке (рис. 28.5).
Рис. 28.5. Схема процесса волочения трубы на подвижной оправке
143
В этом случае силы трения между трубой и оправкой направлены в
сторону движения труб и являются активными, а силы трения трубы о волоку
направлены против движения и являются реактивными.
Трение обрабатываемого металла об инструмент происходит в
присутствии и с участием третьих веществ. К ним относятся окислы
обрабатываемого материала и инструмента, продукты истирания трущихся
поверхностей, смазка и т.п.
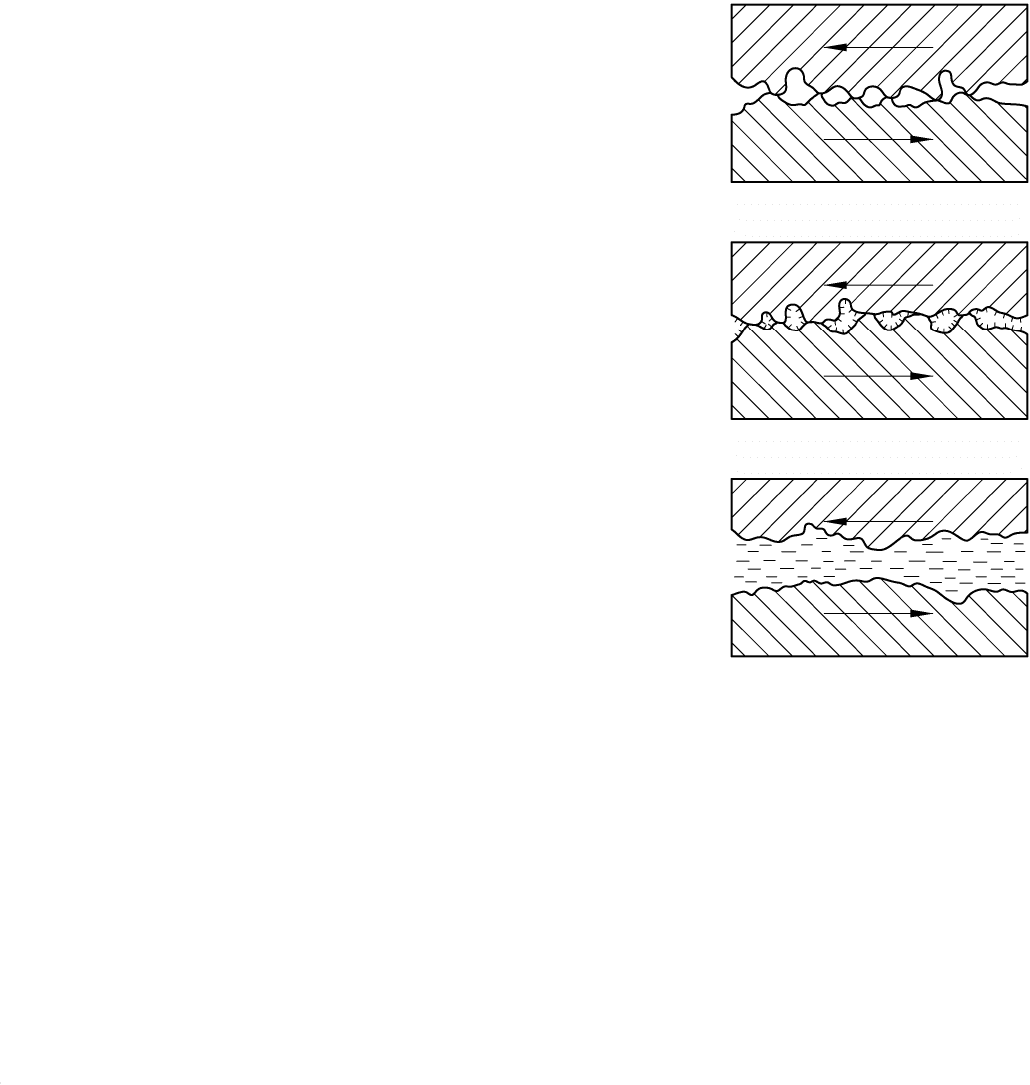
Виды трения (режимы трения) предопределяются количеством и
свойствами этих веществ. Различают три вида трения: сухое, граничное и
жидкостное (рис. 28.6).
Трение называют сухим, если
поверхности обрабатываемого материала и
инструмента находятся во взаимном контакте,
свободны от третьих веществ и происходит
относительное перемещение этих
поверхностей в касательной к ним плоскости.
В чистом виде такой вид трения при ОМД не
встречается, поэтому на практике сухим
трением называют трение несмазанных тел.
Так, горячую прокатку проводят без смазки,
поэтому трение при горячей прокатке условно
называют сухим. Схематичное изображение
его показано на рис. 28.6, а.
Трение называют граничным, если на
поверхности трущихся тел адсорбированы
вещества, существенно отличающиеся
свойствами от материала инструмента и
обрабатываемого тела и при этом имеет место
механическое зацепление шероховатостей
поверхностей контакта. Схема его приведена
на рис. 28.6, б. Это наиболее часто
встречающийся на практике вид трения. Он
имеет место в случае применения смазок без
обеспечения специальных условий, о которых речь пойдет ниже. Смазки,
содержащие поверхностно-активные вещества, адсорбируются на трущихся
поверхностях и образуют прочные пленки. Такие пленки способны
выдерживать высокие нагрузки и оказывают малое сопротивление сдвигу
в
Рис. 28.6. Схематичное
изображение различных
видов трения
а
б

144
этих поверхностей. Однако толщина смазки так мала, что шероховатости
изделия и инструмента находятся во взаимном зацеплении.
Трение называют жидкостным, если между трущимися поверхностями
имеется слой смазки, выводящий из механического зацепления
шероховатости этих поверхностей (рис. 28.6, в). Жидкостное трение - это
внутреннее трение в объеме смазки. Оно нашло применение, например, при
волочении проволоки. Ведутся работы по реализации этого вида трения в
других процессах ОМД. Термин «жидкостное» трение условен, так как
смазка может быть консистентной и даже твердой, например парафин.
Главное, чтобы не происходило соприкосновение трущихся поверхностей, а
сопротивление деформации самой смазки было во много раз меньше
сопротивления деформации обрабатываемого металла.
Отличительная особенность жидкостного трения - давление в слое
смазки. Оно должно быть таким, чтобы могло перевести обрабатываемый
металл в пластическое состояние. В этом случае смазка не будет
выдавливаться из промежутка между трущимися поверхностями, а
деформация изделия инструментом будет осуществляться через слой смазки.
В практических условиях ОМД как сухое, так и жидкостное трение в
чистом виде встречается редко. Это объясняется тем, что, с одной стороны,
на металлическую поверхность всегда попадают вещества, препятствующие
возникновению сухого трения. С другой стороны, при наличии даже
обильной смазки в процессе деформирования металла происходит
вдавливание смазывающей пленки, а также разрушение и потеря ее
физических свойств, что приводит к появлению контактирующих участков,
свободных от смазывающего слоя. Поэтому на практике наблюдается
преимущественно граничное трение.
Контрольные вопросы
1. Основные отличия трения при ОМД и трения в подшипниках.
2. Как влияет контактное трение на неоднородность деформации при ОМД?
3. Как влияет контактное трение на необходимое деформирующее усилие и
работу деформации при ОМД?
4. Как влияет контактное трение на стойкость инструмента при ОМД?
5. Какие различают виды трения?
6. Дайте определение сухого, граничного и жидкостного трения.
7. Какое давление в слое смазки должно быть при жидкостном трении?
8. При каких процессах ОМД силы трения оказывают активное действие?

145
ЛЕКЦИЯ 29
ЗАКОНЫ ТРЕНИЯ И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ
План лекции:
1. Основные показатели, характеризующие условия трения на контакте.
2. Законы трения Амонтона – Кулона и Зибеля.
3. Параметры, определяющие области их предпочтительного применения.
На напряжение трения, являющееся одним из показателей,
характеризующих условия трения на контакте, в общем случае оказывают
влияние такие факторы, как состояние поверхностей инструмента и
деформируемого тела, величина давления, скорость и температура
деформации, наличие и способ подачи смазки и др.
Математически эту зависимость можно записать следующим образом:
τ = τ[σ
n
, ϑ
S
, σ
S
, (ε, ξ, Θ), α] (29.1)
где τ - напряжение трения;
σ
n
- нормальное напряжение на контакте;
ϑ
S
- скорость скольжения металла по инструменту;
σ
S
(ε, ξ, Θ) - сопротивление металла деформации, зависящее, в свою
очередь, от степени ε, скорости ξ и температуры Θ деформации;
α - характеристика физико-химического и механического состояния
контактных поверхностей.
Из-за сложности описания одновременного влияния на напряжение
трения всех перечисленных факторов на практике используют упрощенные
законы трения.
Согласно закону трения Амонтона-Кулона, напряжение трения τ
пропорционально нормальному напряжению на поверхности
контактирующих тел σ
n
и не зависит от сопротивления деформации металла
σ
S
, т.е.
τ = µ ⋅ σ
n
, (29.2)
где µ - коэффициент трения, изменяющийся в пределах от 0,1 до 0,5.

146
В отношении выражения (29.2) необходимо сделать существенную
оговорку. Дело в том, что по условию пластичности максимальная величина
касательного напряжения τ
max
не может быть больше сопротивления
деформации сдвига металла τ
S
, т.е. τ ≤ τ
S
.
Пусть σ
n
при данном µ увеличивается, одновременно возрастает и τ, но
только до тех пор, пока произведение µ ⋅ σ
n
не станет меньше либо равным
τ
S
. При дальнейшем увеличении σ
n
касательное напряжение остается
постоянным, а скольжение частиц металла по поверхности инструмента
затормозится.
Аналогичная картина будет и при изменении µ. Если, например,
нормальное напряжение равно τ
S
, то подстановка в выражение (29.2)
значений µ, больших 0,5, не имеет смысла, и τ определяется как τ
S
.
Использование закона Амонтона-Кулона (29.2) не является
единственно возможным способом учета контактного трения при расчетах
напряженного состояния пластически деформируемых тел. Некоторые
особенности пластического трения, в первую очередь пластическая
деформация контактной поверхности, необратимо приближающая
действительную площадь контакта к номинальной, обусловливают потерю
линейной зависимости напряжения трения от нормального напряжения.
Ряд ученых считают более целесообразным, особенно при горячей
деформации, принимать трение независимым от нормальной нагрузки и
выражать его в долях от величины τ
S
. Этот закон получил название закона
трения по Зибелю и формулируется так: напряжение трения τ
пропорционально среднему по области пластической деформации
сопротивлению деформации сдвига τ
S
и не зависит от приложенного
нормального напряжения σ
n
, т.е.
τ = ψτ
S
, (29.3)
где ψ, в отличие от кулоновского коэффициента трения, называют
показателем трения, изменяющимся в пределах от 0,2 до 1.
Область применения того или иного закона трения наглядно
иллюстрируется графической зависимостью, приведенной на рис. 29.1.
В области умеренных значений нормальных напряжений σ
n
вершина
пластической волны находится в пределах ската шероховатости инструмента,
поэтому в области 1 справедлив закон трения Амонтона-Кулона.
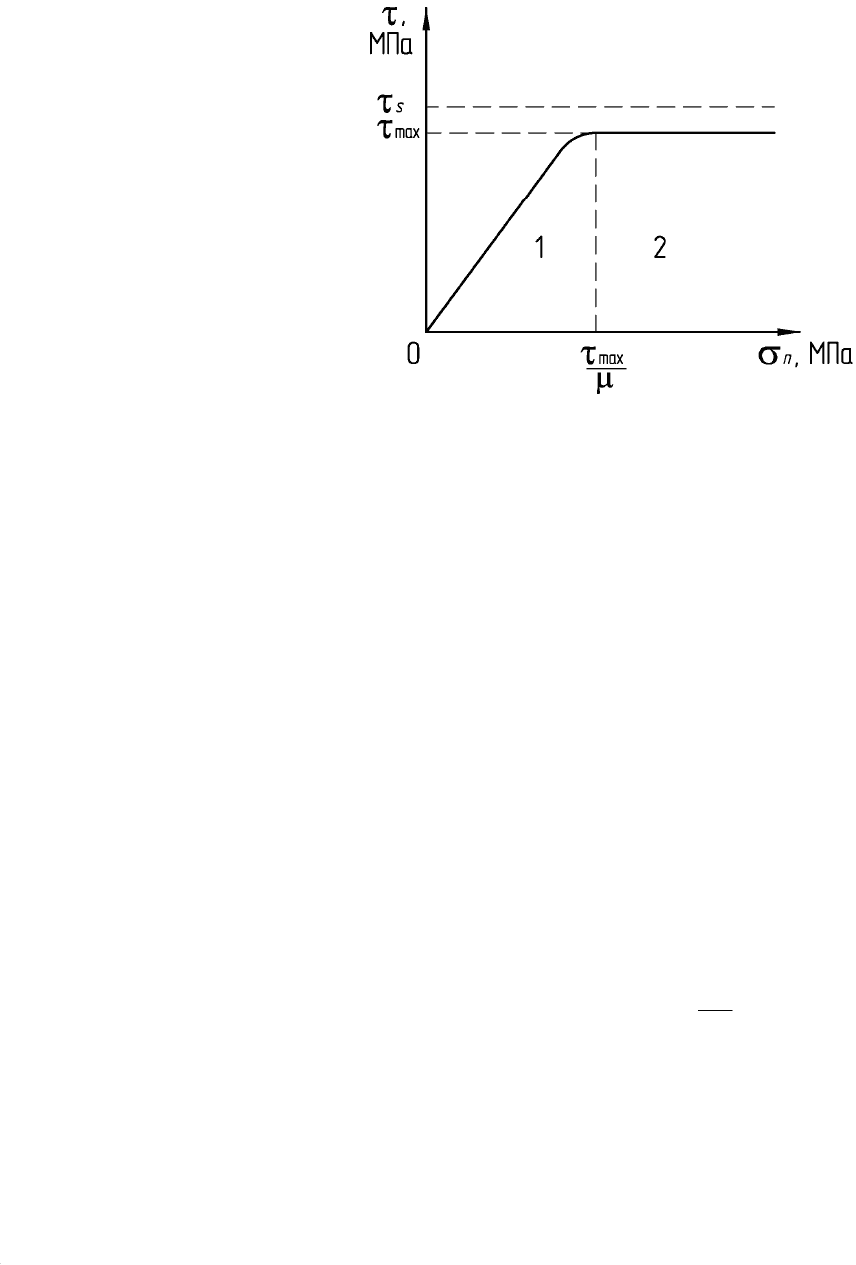
147
При некоторой величине σ
n
пластическая волна заполнит всю впадину
между соседними микроскопическими выступами. После этого дальнейшее
увеличение напряжения σ
n
не изменяет τ и оно остается постоянным (τ ≤ τ
S
).
В области 2 справедлив закон трения по Зибелю.
Рис. 29.1. Диаграмма, характеризующая области применения
того или иного закона трения
Условием (29.3) уместно пользоваться при исследовании процессов
горячей деформации с достаточно выраженным всесторонним сжатием,
например, в случае прессования, или при больших степенях деформации.
Зависимость (29.2) целесообразно использовать при расчете ряда
операций холодной листовой штамповки, а также операций со слабо
выраженной схемой всестороннего сжатия при малых степенях деформации.
Предпринимаются попытки обобщить оба закона трения и
сформулировать один универсальный, позволяющий учесть особенности
использования каждого из них. Так, группой исследователей под
руководством А.Н. Леванова предложен закон трения, выраженный
формулой:
σ
σ
−−ψτ=τ
S
n
S
,251exp1 ,
где σ
S
- сопротивление деформации пограничного слоя.

148
Однако недостатки сформулированного закона не позволяют
рекомендовать его для широкого применения.
Контрольные вопросы
1. Какие факторы оказывают влияние на напряжение трения при ОМД?
2. Сущность закона трения Амонтона-Кулона.
3. Сущность закона трения по Зибелю.
4. В каких пределах изменяется показатель трения ψ?
5. В каких пределах изменяется коэффициент трения µ?
6. В каких случаях предпочтительнее применять законы терния Амонтона-
Кулона и Зибеля. Диаграмма, характеризующая области применения того
или иного закона трения?
7. Какой формулой выражается закон трения предложенный группой
исследователей под руководством А.Н. Леванова?
ЛЕКЦИЯ 30
ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ
НА КОЭФФИЦИЕНТ (ПОКАЗАТЕЛЬ) ТРЕНИЯ.
ТЕХНОЛОГИЧЕСКИЕ СМАЗКИ ПРИ ОМД
План лекции:
1. Влияние на коэффициент трения: состояния поверхности
деформирующего инструмента, свойств обрабатываемого тела, твердости
материала инструмента, температуры деформации, скорости скольжения
металла по инструменту.
2. Технологические смазки при ОМД, их назначение и классификация.
3. Способы нанесения смазки на контактную поверхность.
На величину показателя возникающих на поверхности контакта
элементарных сил трения влияет ряд факторов: состояние поверхности
деформирующего инструмента, состояние поверхности и химический состав
обрабатываемого тела, температура деформации, скорость относительного
скольжения и наличие смазки.
Состояние поверхности рабочего инструмента определяется качеством
обработки поверхности и ее износом в процессе эксплуатации.

149
Чем выше качество обработки поверхности инструмента, тем меньше
при прочих равных условиях коэффициент трения. Влияние обработки
настолько значительно, что величина коэффициента трения различна в
зависимости от направления скольжения металла по отношению к
направлению обработки, которое задается направлением взаимного
перемещения резца или шлифовального круга и обрабатываемого
инструмента. Это явление можно назвать анизотропией трения.
Вид обработки контактной поверхности деформируемого тела имеет
значение лишь в начальный момент деформации. При ее дальнейшем
развитии контактная поверхность деформируемого металла сглаживается и
становится как бы отпечатком поверхности инструмента.
Существенное влияние на коэффициент трения оказывает физико-
химическое состояние поверхности. Однако полной ясности в этом вопросе
нет. Считается, что в случае холодной деформации при тщательной очистке
контактной поверхности от окислов и загрязнений коэффициент трения
достигает максимальных величин, вплоть до того, что может произойти
схватывание (приваривание) трущихся металлов. Это ведет к интенсивному
износу инструмента и, как следствие, к образованию на поверхности
деформируемого тела задиров, царапин и других дефектов.
Экспериментальные исследования о влиянии химического состава
деформируемого сплава на коэффициент трения пока не дают согласных
результатов. Как правило, коэффициент трения имеет меньшие значения,
если трущиеся поверхности относятся к разным металлам. Так, при прокатке
стали на стальных валках коэффициент трения выше, чем на чугунных.
Чем больше твердость инструмента, тем ниже коэффициент трения.
Так, при волочении проволоки наибольший коэффициент трения
наблюдается на стальных, меньший на твердосплавных и еще меньший на
алмазных волоках.
Влияние температуры обрабатываемого металла на коэффициент
трения сложное. При изменении температуры изменяются сопротивление
деформации и физико-химические свойства окалины, образующей
промежуточный слой между металлом и инструментом. Однако установлено,
что при нагревании коэффициент трения сначала растет, достигает
максимального значения, а затем уменьшается. Такой ход зависимости
можно объяснить тем, что сначала коэффициент трения растет в связи с
окислением поверхности и образованием в этом интервале температур

150
твердой окалины. При дальнейшем повышении температуры происходит
размягчение окалины, и она начинает играть роль смазки.
Коэффициент трения несколько снижается с увеличением
относительной скорости скольжения металла по поверхности инструмента,
т.е. с увеличением скорости деформирования. Чем больше скорость, тем
меньше длительность контакта на площадках соприкосновения инструмента
и деформируемого тела и тем меньше роль молекулярного взаимодействия. В
частности, коэффициент трения при обработке на молоте меньше, чем при
обработке на прессе.
При обработке давлением широко применяют смазки, основное
назначение которых – снижение коэффициента трения. Смазка образует
промежуточный слой между деформируемым телом и инструментом,
полностью или частично изолирующий их друг от друга. Для этого она
должна иметь достаточную активность и вязкость.
Активность смазки – способность формировать на поверхности трения
достаточно прочный защитный мономолекулярный слой. Вязкость смазки
обеспечивает ее сопротивление выдавливанию из места контакта трущейся
пары.
Кроме того, смазка должна легко наноситься на поверхность исходной
заготовки и легко удаляться с готового изделия, не должна вступать в
химические реакции с металлом и инструментом, быть безвредной для
окружающих. Для высокотемпературных процессов ОМД смазка должна
обладать хорошими теплоизолирующими свойствами и быть термостойкой.
Все применяемые смазки можно разделить на следующие группы:
1. Жидкие и консистентные смазки – эмульсии, смеси, растительные и
минеральные масла. Эмульсии, представляющие собой смесь воды и
взвешенных в ней мельчайших капелек масла, применяют, главным
образом, при холодной обработке с большими скоростями. При больших
давлениях используют масла и их смеси, обладающие большей вязкостью,
для повышения которой иногда вводят загустители (парафин, стеарин).
Для повышения активности масел к ним добавляют активные
наполнители.
2. Порошкообразные смазки – мыла в виде порошка или стружки, графит.
Последний часто применяют в виде присадки к маслам и в виде водной
суспензии с некоторыми добавками.
3. Стекло в виде порошка или ваты, используемое при горячей обработке
сталей и тугоплавких металлов. При соприкосновении с нагретым
