Загиров Н.Н. Теория обработки металлов давлением

Подождите немного. Документ загружается.

121

Методов определения сопротивления деформации металлов

существует много, но основными (стандартизованными) являются

растяжение, сжатие и кручение.

Испытание на растяжение является одним из распространенных и

простых методов определения σ

, поскольку именно этим способом проще

всего достигается одноосное напряженное состояние, которое сохраняется в

образце до образования шейки.

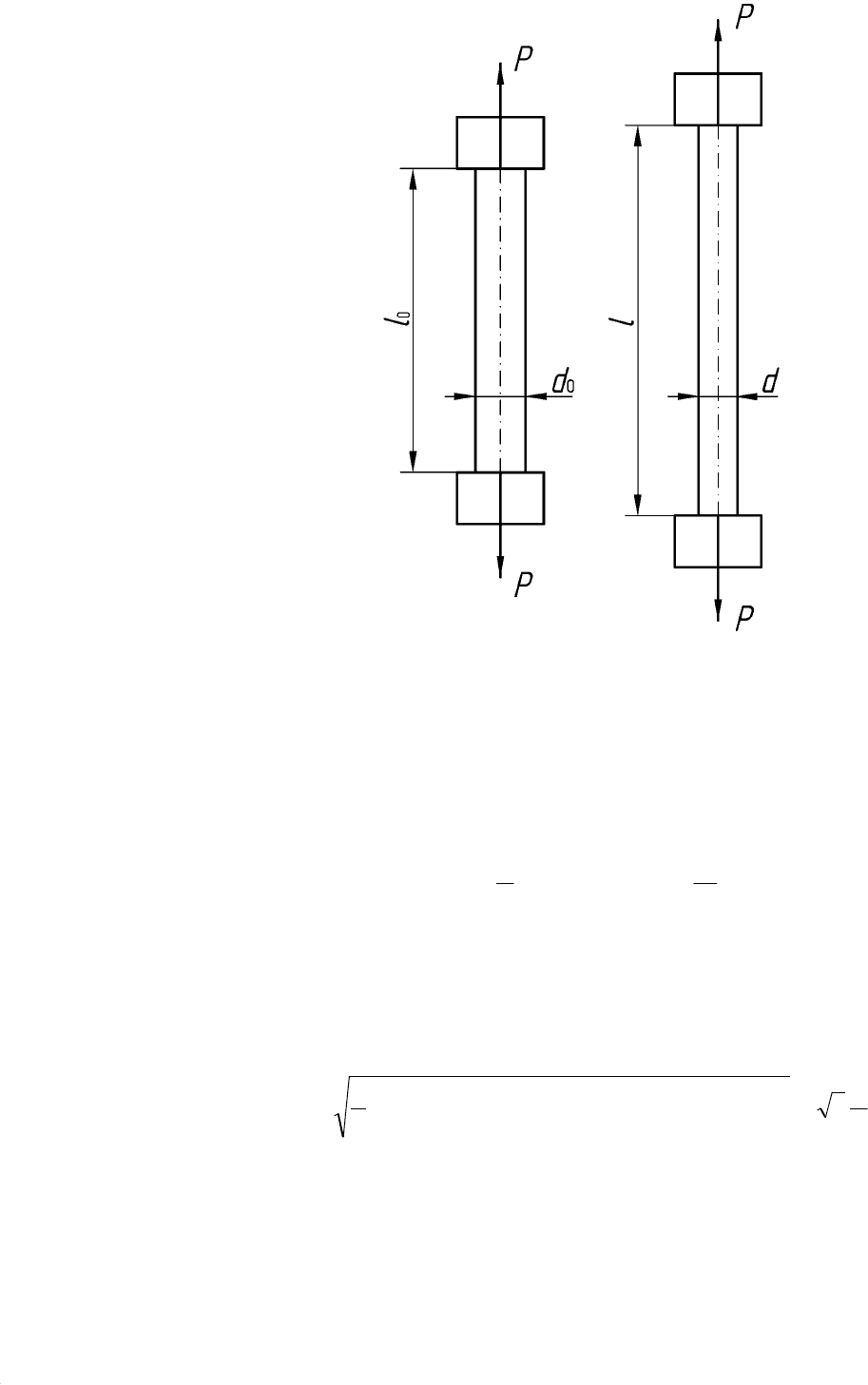
Сущность метода заключается в следующем. Образец (рис.24.1) с

соотношением размеров рабочей части l

/ d

= 5...10 (ГОСТ 1497 - 73)

растягивают силой Р, при этом относительная скорость перемещения

захватов испытательной машины составляет ϑ.

По ходу опытов в каждый момент времени регистрируют силу

растяжения Р образца и величину абсолютного его удлинения ∆l = l - l

Обработав соответствующим образом первичную диаграмму растяжения в

координатах сила - абсолютное удлинение, можно получить диаграмму

истинных напряжений. Для этого принимается допущение, что при

растяжении во всем образце имеет место однородное одноосное напряженное

состояние. Ось образца совпадает с одной из осей главных нормальных

напряжений и главных удлинений, тогда компоненты тензора напряжения

=σ=σ

; σ

= σ

= 0, (24.1)

где

∆+

(24.2)

- текущая площадь поперечного сечения образца.

122

Рис. 24.1. Образец до и после испытания

для определения сопротивления деформации методом растяжения

Компоненты тензора скорости деформации:

=ξ ;

3322

−=ξ=ξ .

Подставив величины ξ

, ξ

в формулу для нахождения

интенсивности скоростей деформаций сдвига Н, получим:

( ) ( ) ( )

[

]

1133

3322

2211

=ξ−ξ+ξ−ξ+ξ−ξH

Степень деформации сдвига при развитом пластическом растяжении:

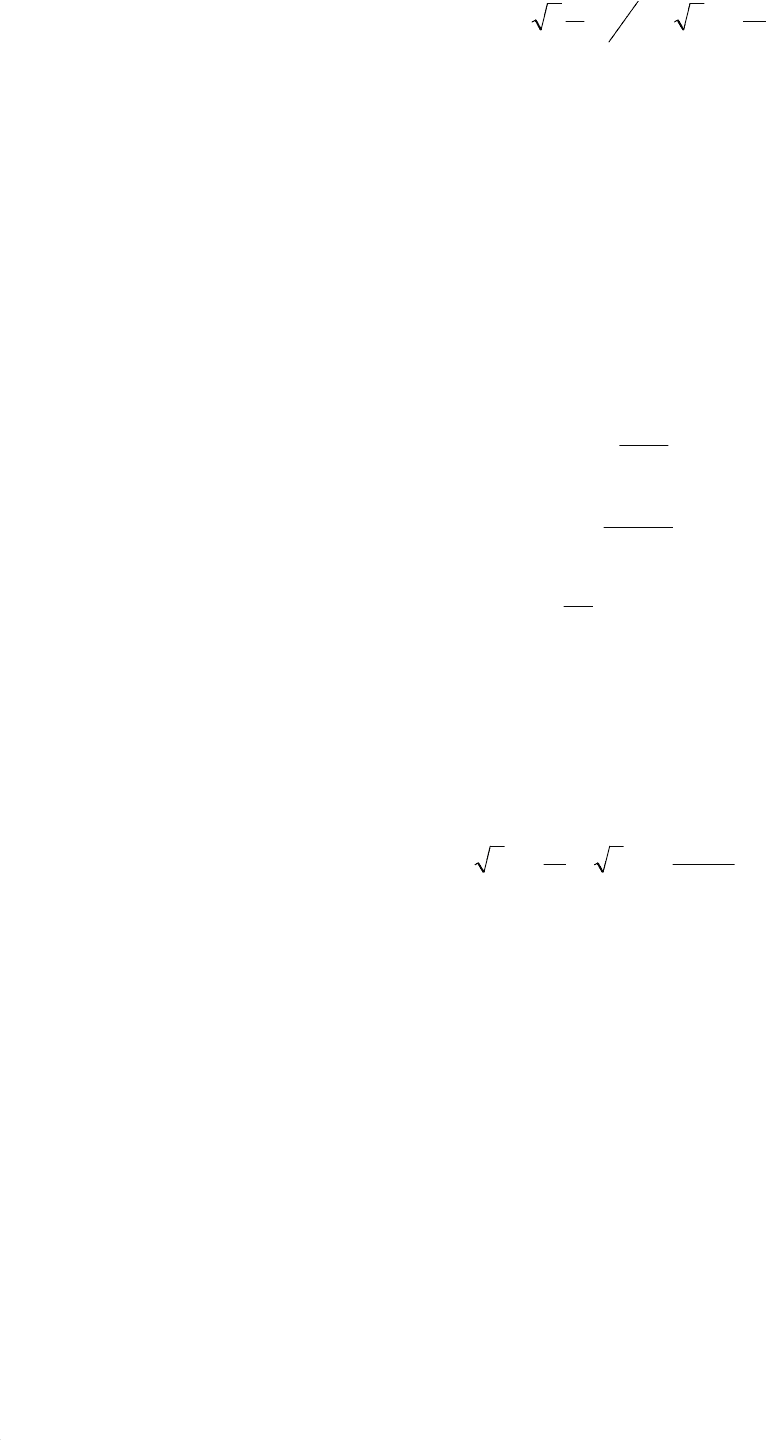
123

(

)

ln3

⋅=

∫

τ=λ , (24.3)

где l = l

+∆l - текущая длина образца.

Таким образом, диаграмма Р∼∆l путем несложного пересчета в

соответствии с формулами (24.1) и (24.3) превращается в диаграмму σ

∼ λ,

по оси ординат которой откладывают сопротивление деформации σ

, а по оси

абсцисс - степень деформации сдвига λ.

В зависимости от вида характеристики относительной деформации при

растяжении в качестве ее показателя наряду с λ могут выступать

(обозначение условное):

а) относительное удлинение - %

100

⋅=δ ;

б) относительное сужение - %

100

⋅=ψ ;

в) истинное сужение -

ln=ϕ .

В пределах равномерного удлинения образца, т.е. до момента

образования шейки, между ними легко установить определенные

соотношения, воспользовавшись условием постоянства объема (24.2). Так,

например:













⋅=⋅=λ 1

100%

ln3ln3

Несмотря на простоту и отработанность методики

экспериментирования, испытание на растяжение обладает рядом

недостатков. При сравнительно небольшой деформации нарушается

однородность ее распределения, образуется шейка, напряженное состояние

значительно отклоняется от одноосного. Для многих металлов и сплавов

образование шейки начинается уже при λ = 0,3...0,5. Другим недостатком

метода является низкая скорость деформации, так как на стандартных

разрывных машинах средняя скорость не превышает 0,1 с

-1

. На практике

обработка металлов давлением осуществляется чаще всего с деформациями и

скоростями, превышающими указанные значения.

124

Методом определения сопротивления деформации металлов и сплавов,

позволяющим осуществлять деформацию до значительно больших величин,

чем при растяжении, является осадка цилиндрических образцов плоскими

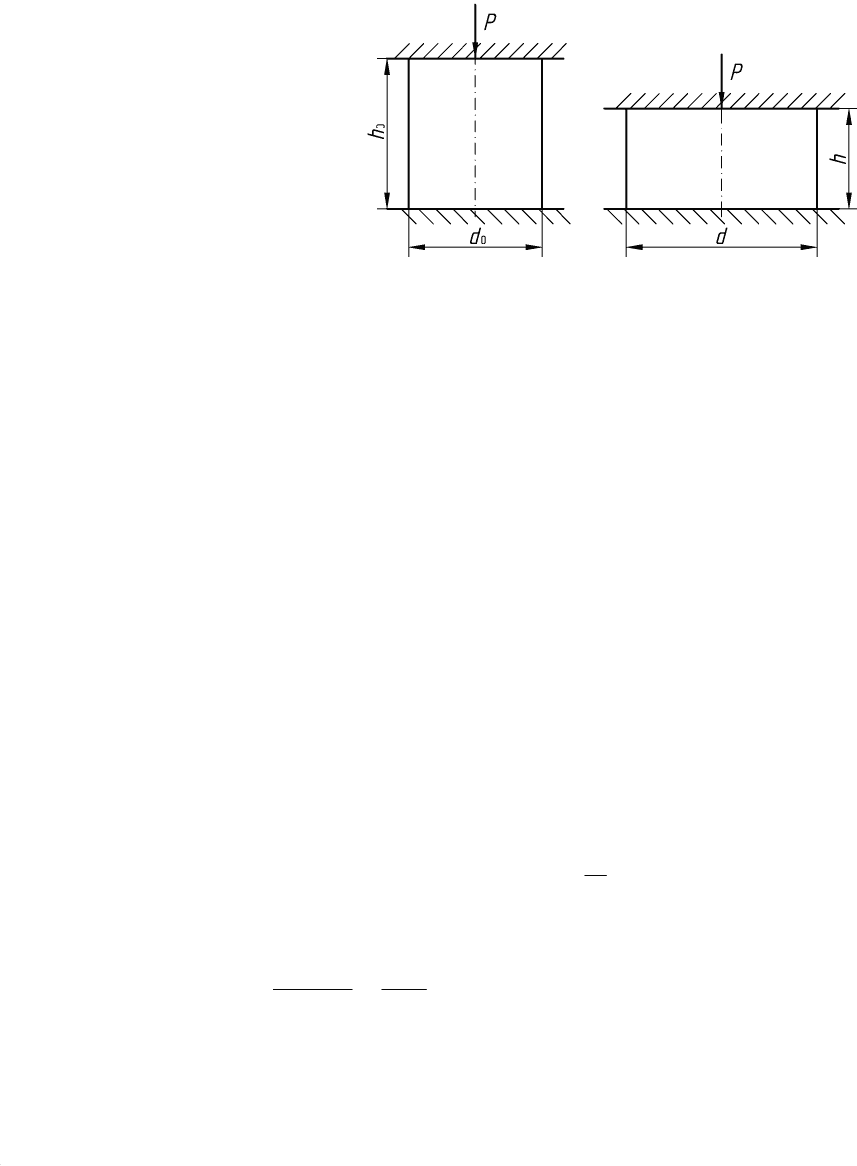
полированными бойками (рис.24.2).

Для испытания применяются образцы с отношением высоты к

диаметру 1< h

/ d

< 2. Осадка низких образцов сопровождается искажением

опытных данных из-за влияния трения, высокие образцы теряют

устойчивость, получая продольный изгиб.

Рис. 24.2. Схема испытания для определения сопротивления деформации

методом сжатия

В принципе испытания на осадку носят непрерывный характер, однако

обычно осадку образца осуществляют до тех пор, пока его высота не

уменьшится на 50...70%. Потом процесс прекращают, образец извлекают,

обтачивают до получения соотношения размеров 1 < h / d <2 и продолжают

его осадку. В результате можно получить большие степени пластической

деформации.

Диаграмма Р ∼ ∆h (сила сжатия - уменьшение высоты образца или

абсолютное обжатие), полученная в ходе испытаний, может быть легко

перестроена в переменных σ

∼ λ. Для этого необходимо воспользоваться

соотношениями:

для нахождения σ

=σ

(24.4)

где

∆−

- текущее значение площади поперечного сечения

образца;

125

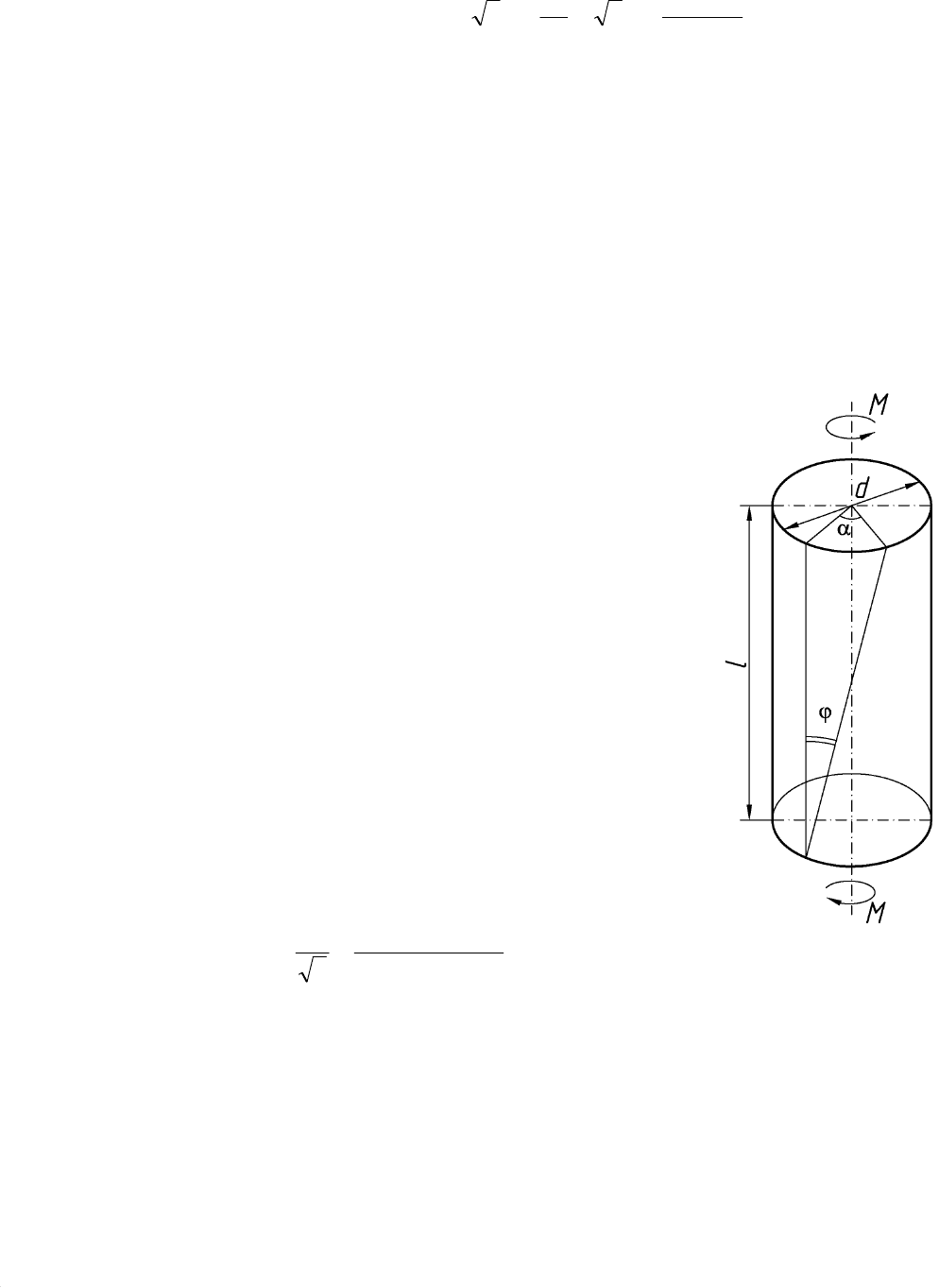
Рис. 24.3. Параметры

образца для определения

сопротивления деформации

методом кручения

для нахождения λ (вывод аналогичен приведенному выше):

∆−

⋅=⋅=λ

ln3ln3 . (24.5)

При испытании на осадку отрицательным фактором является

невозможность точной оценки величины сил трения между деформирующим

инструментом и деформируемым материалом. Несмотря на хорошую смазку

и специальную обработку рабочих поверхностей инструмента, часто не

удается избежать искажения боковой поверхности образца

(бочкообразования), что свидетельствует об отклонении напряженного

состояния от линейного.

Большие деформации удается получить и при скручивании сплошных

образцов (рис. 24.3). Преимуществами этого

метода являются отсутствие смещения металла

относительно инструмента и вследствие этого

исключение трения на контактных

поверхностях, а также возможность

варьирования степени и скорости деформации в

широких пределах. Однако сплошные образцы

не удовлетворяют требованию о неизменности

на протяжении всего испытания напряженного

и деформированного состояний.

Преодолеть это удается, подвергая

кручению два образца разных диаметров. В

этом случае определяют сопротивление

деформации сдвига условно-трубчатого

образца:

(

)

( )

−

⋅

=τ , (24.6)

где d

> d

- диаметры образцов; М

> М

моменты при скручивании образцов.

126

Степень деформации сдвига λ рассчитывается по формуле

⋅

=ϕ=λ

tg ,

где ϕ - угол наклона риски, первоначально нанесенной на боковую

поверхность образца параллельно образующей;

α - относительный угол поворота торцов образца;

l - длина образца.

Как недостаток этого метода можно отметить локализацию

деформации то в одном, то в другом сечении по длине образца, что

затрудняет определение величины истинной деформации.

Контрольные вопросы

1. Какими методами определяют сопротивление металла пластической

деформации?

2. Какова предельная деформация при растяжении, не приводящая к

образованию шейки?

3. Какие принимаются допущения при построении диаграммы истинных

напряжений при растяжении?

4. Преимущества и недостатки различных методов определения

сопротивления металла пластической деформации.

5. С каким отношением высоты к диаметру применяются образцы при

осадке?

6. До каких пор обычно осуществляют осадку образца?

7. Какими показателями характеризуется величина деформации при

различных методах испытаний?

ЛЕКЦИЯ 25

СОПРОТИВЛЕНИЕ ДЕФОРМАЦИИ ПРИ ХОЛОДНОЙ ОБРАБОТКЕ

План лекции:

1. Сопротивление деформации при холодной обработке.

2. Механизм и графическое изображение упрочнения при холодной

деформации.

3. Анизотропия свойств получаемых изделий.

127

4. Текстура деформации.

5. Гипотеза единой кривой.

Основным показателем, влияющим на сопротивление деформации при

холодной обработке, является степень деформации. Зависимость между

сопротивлением деформации и степенью деформации изображают кривыми

упрочнения, при построении которых по оси ординат обычно откладывают

сопротивление металла пластической деформации σ

, а по оси абсцисс -

относительную деформацию. В некоторых случаях по оси абсцисс

откладывают логарифмическую деформацию, удобство использования

которой заключается в том, что логарифмические деформации обладают

свойством аддитивности (результирующая деформация равна сумме

промежуточных деформаций), и, кроме того, в том, что логарифмические

деформации, выраженные через изменение линейных размеров, при

растяжении и сжатии являются эквивалентными по упрочняющему эффекту.

При холодной ОМД с увеличением степени деформации повышаются

все показатели прочности, в том числе и сопротивление деформации.

Увеличение σ

особенно интенсивно происходит на начальных стадиях

деформации (до λ≈0,5 %), при дальнейшем повышении степени деформации

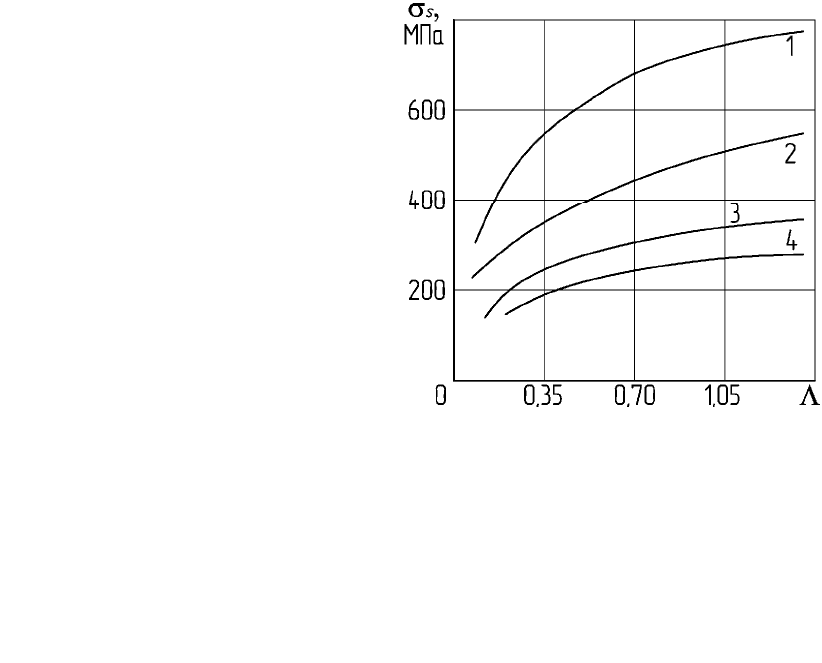
интенсивность упрочнения снижается. Характер кривых упрочнения для

некоторых металлов и сплавов показан на рис. 25.1.

Рис. 25.1. Кривые упрочнения для некоторых металлов и сплавов:

1 - никель НП2; 2 - латунь Л63; 3 - медь М1; 4 - дюралюминий Д1.

128

Опыты показывают, что для большинства металлов (для которых

температура обработки не равна и не выше температуры рекристаллизации)

зависимость σ

= f(λ) не чувствительна к скорости деформации. Металлы в

холодном состоянии не проявляют вязких свойств.

В соответствии со схемой деформации изменяется и форма зерен - в

направлении деформации растяжения они вытягиваются, а в направлении

деформации сжатия - уменьшаются. Такое строение приводит к тому, что

механические свойства наклепанного металла будут неодинаковы в разных

направлениях, т.е. металл становится анизотропным.

Кроме того, с изменением формы зерен происходит упорядочение

ориентировки их решетки в результате кристаллографической

направленности скольжения по определенным плоскостям и направлениям,

образуется текстура деформации.

Появление текстуры деформации наблюдается при некоторой степени

деформации (примерно 0,8...1,0), и с ее ростом увеличивается и степень

совершенства текстуры. Поэтому образование текстуры деформации играет

большую роль в таких процессах ОМД, как холодная прокатка тонких листов

и лент, волочение проволоки, где степень деформации достигает больших

значений.

Кривыми упрочнения можно пользоваться для анализа характера и

степени влияния упрочнения на величину необходимых при ОМД усилий

деформирования. С этой целью широкое распространение получила

свойственная холодной обработке так называемая гипотеза единой кривой,

сущность которой заключается в следующем: функции Т = Т(Н) и σ

= σ

(λ),

связывающие инвариантные характеристики напряженного и

деформированного состояний, не зависят от вида деформации (растяжение,

сжатие, кручение и т.п.), каким они получены, определяются в простейших

опытах, а результаты могут быть использованы при анализе сложных

процессов ОМД. Важно лишь правильно подсчитать степень деформации и

интенсивность напряжений.

Для облегчения аналитического решения задачи по установлению

влияния упрочнения на величину усилия деформирования и на

распределение напряжений в деформируемом теле, необходимо кривую

упрочнения представить в виде уравнения, связывающего сопротивление

деформации со степенью деформации.

129

Математическая модель, удовлетворительно описывающая кривую

упрочнения для развитых деформаций, существенно превышающих упругие,

имеет вид:

= a ⋅ λ

где a, b - эмпирические коэффициенты, которые выбирают из условия

лучшей аппроксимации опытных данных.

Как при построении кривых упрочнения, так и при анализе процессов

деформации, следует учитывать, что при холодной деформации около 90 %

работы переходит в тепло и что происходящий разогрев существенно влияет

на ход кривых упрочнения.

Контрольные вопросы

1. Какова зависимость сопротивления металла пластической деформации от

степени деформации?

2. В виде какой математической модели представляют кривую упрочнения?

3. Что такое «анизотропия»?

4. Что такое «текстура деформации»?

5. В чем выражается свойство аддитивности деформации?

6. Сущность гипотезы единой кривой.

ЛЕКЦИЯ 26

СОПРОТИВЛЕНИЕ ДЕФОРМАЦИИ

ПРИ ПОВЫШЕННЫХ ТЕМПЕРАТУРАХ

План лекции:

1. Сопротивление деформации при повышенных температурах.

2. Понятие о скорости деформации и скорости деформирования.

3. Конструкция и принцип действия кулачкового пластометра для

определения сопротивления деформации.

В общем случае сопротивление деформации σ

при горячей обработке

зависит от степени деформации ε, температуры

, скорости деформации ξ и

истории деформирования ε(t). Знать сопротивление деформации при высоких

температурах особенно важно, так как практически весь выплавленный

130

металл, если он подвергается пластической деформации, проходит стадию

высокотемпературной обработки.

При изучении процессов, происходящих в металле при повышенных

температурах, вводят понятие гомологической или сходственной

температуры Θ, под которой понимают отношение текущей изучаемой

температуры Т к температуре плавления Т

пл

данного металла (выражается в

кельвинах). Так, гомологическая температура рекристаллизации составит 0,4.

ЕслиΘ

обр

≥ 0,4, то деформация осуществляется вместе с рекристаллизацией

и является горячей.

Кроме того, в отличие от холодной обработки сопротивление

деформации при горячей обработке в значительной степени зависит от

скорости деформации.

Как известно, скоростью деформации называется изменение степени

деформации в единицу времени:

=ξ ;

=ξ

Так как относительные деформации (δ, ε) – величины безразмерные, то

размерностью скорости деформации будет 1/с.

От скорости деформации следует отличать скорость деформирования –

скорость перемещения деформирующего инструмента, имеющую

размерность м/с. При одной и той же скорости деформирования скорости

деформации могут быть различными.

Покажем это на примере равномерного растяжения двух образцов

разной длины при одинаковой скорости деформирования υ – скорости

перемещения зажим разрывной машины. В этом случае за один и тот же

промежуток времени dt образцы получат одинаковое абсолютное удлинение

∆l = υdt.

Относительные удлинения и скорости деформации образцов будут

разные:

∆

=δ ;

∆

=δ ;

t dd

∆

=ξ ;

t dd

∆

=ξ