Yung Y.L., DeMore W.B. Photochemistry of Planetary Atmospheres
Подождите немного. Документ загружается.

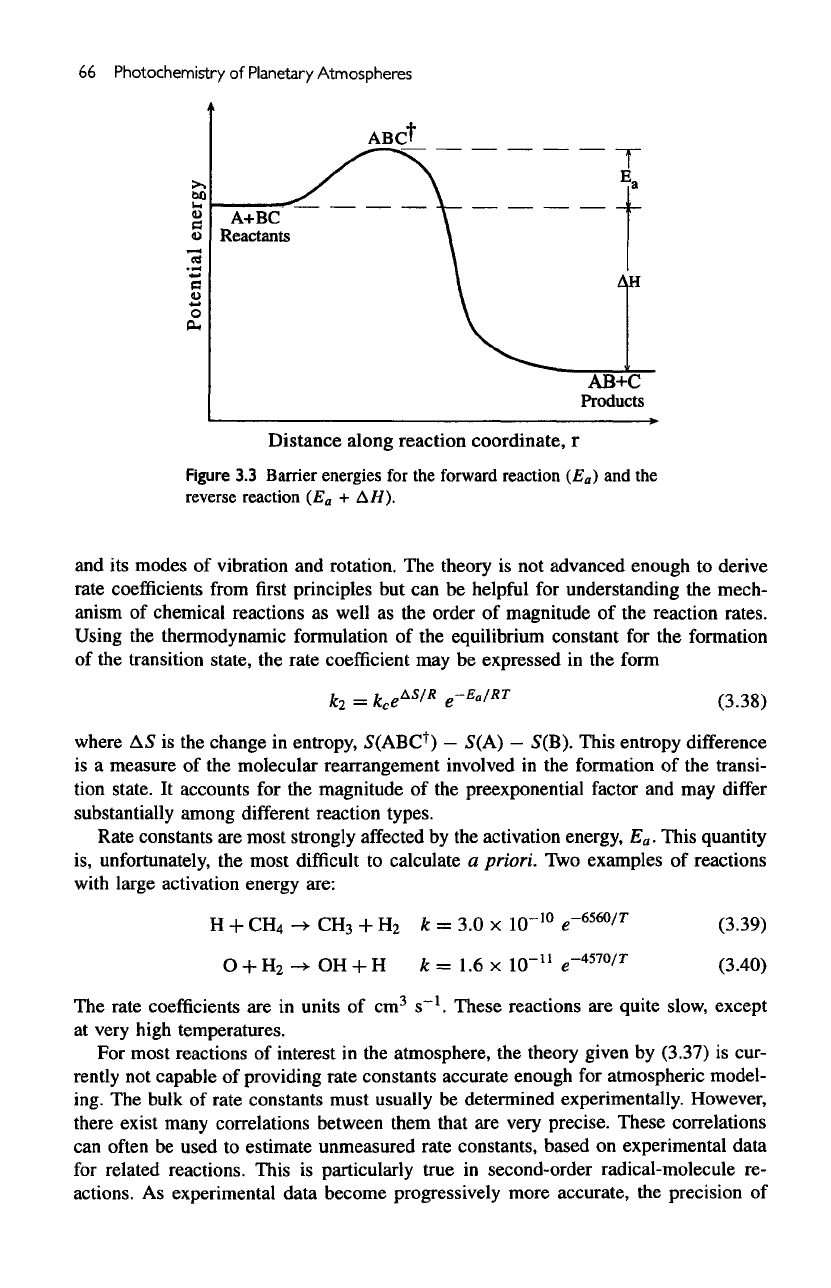
66
Photochemistry
of
Planetary
Atmospheres
Figure
3.3
Barrier
energies
for the
forward reaction
(E
a
)
and the
reverse reaction
(E
a
+
AH).
and
its
modes
of
vibration
and
rotation.
The
theory
is not
advanced enough
to
derive
rate coefficients
from
first
principles
but can be
helpful
for
understanding
the
mech-
anism
of
chemical reactions
as
well
as the
order
of
magnitude
of the
reaction rates.
Using
the
thermodynamic
formulation
of the
equilibrium constant
for the
formation
of
the
transition state,
the
rate
coefficient
may be
expressed
in the
form
where
AS is
the
change
in
entropy,
5(ABC
f
)
-
5(A)
-
5(B).
This entropy difference
is
a
measure
of the
molecular rearrangement involved
in the
formation
of the
transi-
tion
state.
It
accounts
for the
magnitude
of the
preexponential factor
and may
differ
substantially
among
different
reaction types.
Rate constants
are
most strongly affected
by the
activation energy,
E
a
.
This quantity
is,
unfortunately,
the
most
difficult
to
calculate
a
priori.
Two
examples
of
reactions
with
large activation energy
are:
The
rate
coefficients
are in
units
of
cm
3
s"
1
.
These
reactions
are
quite slow, except
at
very
high temperatures.
For
most reactions
of
interest
in the
atmosphere,
the
theory given
by
(3.37)
is
cur-
rently
not
capable
of
providing rate constants accurate enough
for
atmospheric model-
ing.
The
bulk
of
rate constants must usually
be
determined experimentally. However,
there
exist many correlations between them that
are
very precise.
These
correlations
can
often
be
used
to
estimate unmeasured rate
constants,
based
on
experimental data
for
related reactions. This
is
particularly true
in
second-order radical-molecule
re-
actions.
As
experimental data become progressively more accurate,
the
precision
of
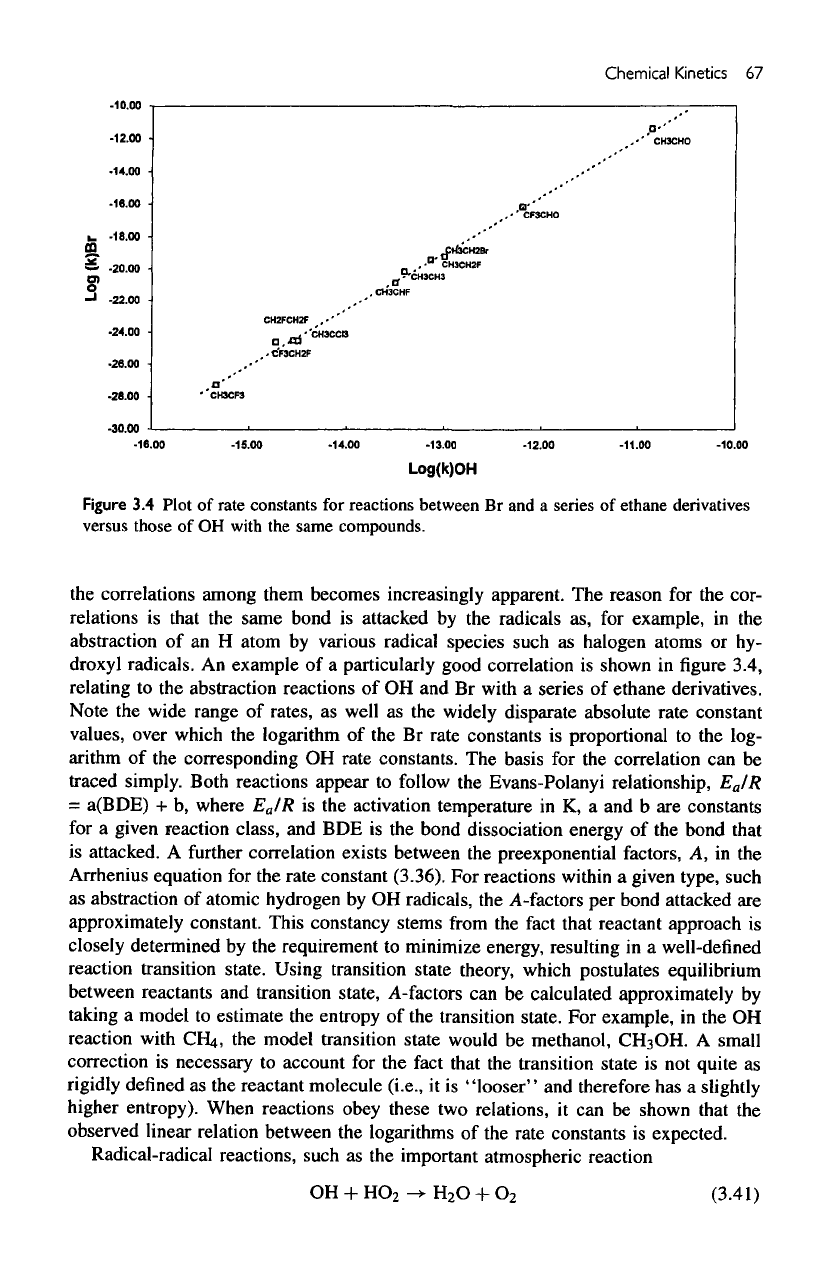
Chemical
Kinetics
67
Figure
3.4
Plot
of
rate constants
for
reactions between
Br and a
series
of
ethane derivatives
versus those
of OH
with
the
same compounds.
the
correlations among them becomes increasingly apparent.
The
reason
for the
cor-
relations
is
that
the
same bond
is
attacked
by the
radicals
as, for
example,
in the
abstraction
of an H
atom
by
various radical
species
such
as
halogen atoms
or
hy-
droxyl
radicals.
An
example
of a
particularly good correlation
is
shown
in figure
3.4,
relating
to the
abstraction reactions
of OH and Br
with
a
series
of
ethane derivatives.
Note
the
wide range
of
rates,
as
well
as the
widely
disparate
absolute rate constant
values, over which
the
logarithm
of the Br
rate constants
is
proportional
to the
log-
arithm
of the
corresponding
OH
rate constants.
The
basis
for the
correlation
can be
traced simply. Both reactions
appear
to
follow
the
Evans-Polanyi
relationship,
E
a
IR
=
a(BDE)
+ b,
where
E
a
IR
is the
activation temperature
in K, a and b are
constants
for
a
given reaction class,
and BDE is the
bond dissociation energy
of the
bond that
is
attacked.
A
further
correlation exists between
the
preexponential factors,
A, in the
Arrhenius
equation
for the
rate constant
(3.36).
For
reactions
within
a
given type, such
as
abstraction
of
atomic hydrogen
by OH
radicals,
the
A-factors
per
bond attacked
are
approximately
constant. This constancy stems
from
the
fact
that reactant approach
is
closely determined
by the
requirement
to
minimize energy, resulting
in a
well-defined
reaction transition state. Using transition state theory, which postulates equilibrium
between reactants
and
transition state, A-factors
can be
calculated approximately
by
taking
a
model
to
estimate
the
entropy
of the
transition state.
For
example,
in the OH
reaction with
CRt,
the
model transition state would
be
methanol,
CH
3
OH.
A
small
correction
is
necessary
to
account
for the
fact
that
the
transition state
is not
quite
as
rigidly
defined
as the
reactant molecule (i.e.,
it is
"looser"
and
therefore
has a
slightly
higher
entropy). When reactions obey these
two
relations,
it can be
shown
that
the
observed linear relation between
the
logarithms
of the
rate constants
is
expected.
Radical-radical reactions, such
as the
important atmospheric reaction

68
Photochemistry
of
Planetary
Atmospheres
Figure
3.5
Capture
cross
section
for
ion-molecule collisions.
After
Su,
T,
and
Bowers,
M.
T.,
1979,
"Classical
Ion-Molecule Collision
Theory,"
in
Bowers
(1979;
cited
in
section 3.1),
p. 83.
are not as
well understood
as
radical-molecule reactions.
These
reactions
often
have
zero
or
negative activation
energies,
since
the
energy
input
associated
with
bond break-
ing
is
very small. Higher energy
in the
reactants
may
actually reduce
the
reaction
probability.
Another
difference
exists
is
that, though reaction (3.41)
is
nominally
an
OH
abstraction
of an H
atom,
the
limited approach geometry related
to
energy mini-
mization
is not
required.
As a
result,
the
effective
preexponential factor
is
very
high
and
is
difficult
to
estimate based
on any
model structure
of the
transition
state.
3.4.4
Ion-Molecule
Reactions
For
ions colliding
with
neutrals,
the
effective
cross section
is
much larger than that
for
neutral-neutral collisions, because atoms
and
molecules
are
polarizable,
and the ion
with
charge
q at
distance
r can
induce
a
dipole.
The
subsequent interaction between
the
ion and the
induced dipole
can be
described
by an
attractive potential:
where
or is the
polarizability
(in
units
of
cm
3
)
of the
atom
or
molecule. This attractive
potential
has two
important
effects
on the
rate
coefficient:
(a)
increase
the
collision
cross
section,
and (b)
increase
the
energy
of the
collision such that
the
activation
energy
is
easily overcome. Note that
(a) is due to the
long-ranged Coloumb force
and
(b) is
from
the
conversion
of
potential energy
to
kinetic energy.
The
mechanics
for the
interaction between
an
incident
ion (A) and a
neutral particle
(B)
are
shown
in figure
3.5.
The
masses are, respectively,
m\
and
m^.
The
impact
parameter
is b, and the
initial velocity
is
vg.
The
effective
potential
is
where
we
have added
the
repulsive centrifugal potential
due to the
angular momentum
(L)
of the
system
and
//.
is the
reduced mass
m^m^/(m
A
+
m^).
Since angular
momentum
is
conserved,
L is
nvob,
a
constant.
V
e
ff
has two
parts.
At
large distance
the
repulsive
(centrifugal)
part dominates;
at
small distance
the
attractive (induced dipole)
part
becomes
more important.
An
example
for
N2
+
+ N2 is
given
in figure
3.6.
The
distance
at
which
the
repulsive
and the
attractive forces balance
is the
critical distance
r
c
,
given
by
solving
the
equation

Chemical
Kinetics
69
Figure
3.6
Plot
of
V
e
ff
versus
r for
N2
+
colliding
with
N2-
After
Su,
T.,
and
Bowers,
M.
T.,
1979,
"Classi
Theory,
section
cal
Ion-Molecule
Collision
"
in
Bowers
(1979;
cited
in
3.1),
p. 83.
The
result
is
The
critical distance
has a
special physical meaning.
All
collisions that pass within
result
in a
capture.
At r =
r
c
the
energy needed
to get
over
the
centrifugal barrier
r
c
is
However,
at
r
c
all the
energy
is in the
tangential motion.
E
c
is
then
the
total energy
mvi/2.
Hence,
we can
solve
for the
critical impact parameter
b
c
:
The
rate
coefficient
is
given
by
This
is
known
as the
Langevin rate constant
for
ion-molecule reactions. Ion-molecule
reactions
are
usually faster than neutral-neutral reactions,
as
shown
in the
following
examples:
where
the
units
of the
rate
coefficients
are
cm
3
s~'.

70
Photochemistry
of
Planetary Atmospheres
3.5
Termolecular
Reactions
In
section 3.4,2
we
pointed
out the
difficulty
of
forming
a new
chemical bond because
of
the
need
to
dissipate
a
large amount
of
energy (the bond energy)
in a
short time
(the collision time) over
a
small amount
of
space
(the
size
of the
molecule).
One
way
to
stabilize
the new
bond
is to
invoke collision with
a
third body. Consider
the
association
of the
reactants
A and B
forming
an
association complex
AB^:
The
complex
can
decay
via a
unimolecular
reaction:
or can be
stabilized
by
collision
with
the
background
gas M:
The net
result
may be
summarized
as
with
an
effective
three-body rate
coefficient
This
is
known
as the
Lindemann-Hinshelwood rate
coefficient.
At low
pressure
we
have
In
this
case
the
most critical parameter that determines
the
value
of
&LH
is the
lifetime
l/kb
of the
association complex
AB^
The
lifetime
of the
association complex
may
be
estimated using
the
Rice-Ramsperger-Kassel-Marcus
theory.
In
general,
a
simple
association
complex like
H2
f
or
O^
has
only
one
vibrational mode,
and all the
excess
energy
in the
excited molecule
is
available
for
breaking
the
bond.
The
lifetime
is
short,
resulting
in
small values
of
rate coefficients:
where
the k
values
refer
to
room temperature
in
units
of
cm
6
s~'.
Compare
the
above
rate
coefficients with
those
for
more complex reactions such
as
These
rate coefficients
are
many orders
of
magnitude greater than those
for
(3.58)
and
(3.59).
The
reason
is as
follows:
The
activated complexes
CH^
and
C2H6
f
have
Chemical
Kinetics
7
1
8 and 18
vibrational modes, respectively.
The
excess bond energy
is
distributed over
many
degrees
of
freedom.
It
would take thousands
of
vibrations before
the
excess
energy
could
be
concentrated into
one
particular bond that breaks.
The
lifetime
of
the
association complex
is
long,
and by
(3.57),
this implies
a
fast
rate
of
formation.
The
high
rate coefficients
for the
synthesis
of
complex organic molecules explain
the
abundance
of
these compounds
in the
atmosphere
of
Titan
and
have implications
for
the
origin
of
life.
The
high-pressure
limit
of
(3.56)
is
In
this
case
the
rate
of
reaction
(3.55)
is
In
this limit
the
three-body
reaction
reduces
to a
two-body
reaction,
with
rate
given
by
the
rate-limiting reaction
(3.52).
Physically,
at
high pressure
the
quenching
is so
efficient
that every association complex formed
by
(3.52)
is
eventually stabilized
by
collisions.
The
Lindemann-Hinshelwood
mechanism
does
not
give
a
good
approximation
to
the
experimental data
in the
"falloff'
region, that
is, in the
transition region between
two-body
and
three-body limits.
An
improvement
to the
Lindemann-Hinshelwood
theory
is
given
by
Troe;
we
state without derivation
his
formula
for
three-body rate
coefficient:
where
£
LH
is
*
0
/(1
+
(*ot
&*]/*«,)
from
(3.56)
and X = log
(fc
0
[M]//fc
TO
).
Note
that
the
correction factor
from
Tree's
equals
unity
when
M
->
0 or
oo.
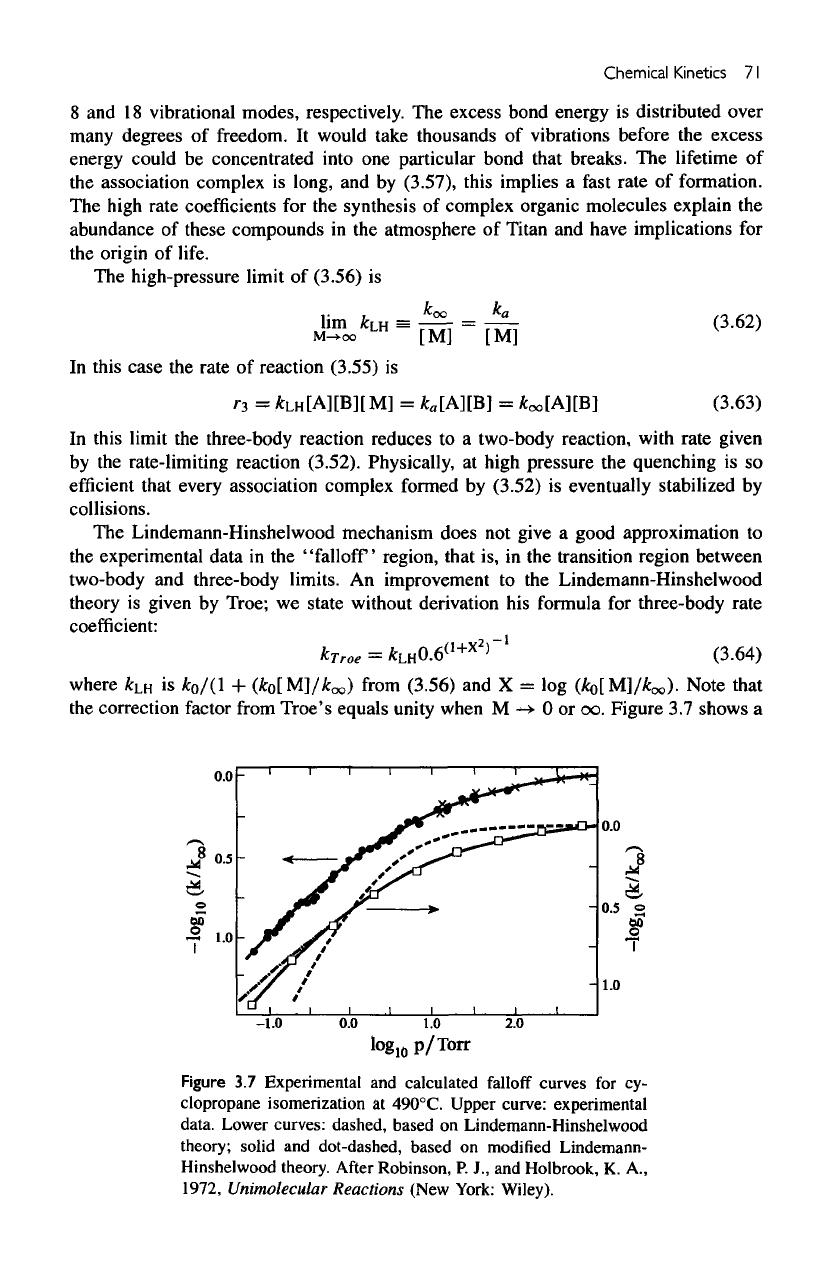
Figure
3.7
shows
a
Figure
3.7
Experimental
and
calculated
falloff
curves
for cy-
clopropane
isomerization
at
490°C.
Upper
curve:
experimental
data.
Lower
curves:
dashed,
based
on
Lindemann-Hinshelwood
theory;
solid
and
dot-dashed,
based
on
modified Lindemann-
Hinshelwood
theory. After
Robinson,
P. J., and
Holbrook,
K.
A.,
1972,
Unimolecular
Reactions
(New York: Wiley).
72
Photochemistry
of
Planetary Atmospheres
Figure
3.8
Rate
coefficient
for
CIO
+
CIO
+
N
2
-»•
(C1O)
2
+
Nj
as a
function
of
N
2
concentrations
over
the
temperature
range
from
194
to
247 K. The
dashed
line
is
extrapolated
from
earlier
work.
After
Sander,
S. P,,
Friedl,
R. R.,
and
Yung,
Y.
L.,
1989, "Rate
of
Formation
of
CIO
Dirner
in
Polar
Stratospheric
Chemistry:
Implications
for
Ozone
Loss."
Science
245, 1095.
comparison
of the
Lindemann-Hinshelwood theory
and its
modified form
for
providing
an
empirical
fit to
experimental data.
Figure
3.8
shows
a
laboratory determination
of the
rate coefficient
for the
reaction
CIO
+
CIO
+
N
2
->•
(C1O)
2
+
N
2
as a
function
of
N
2
concentrations.
The
results
suggest that
it is
difficult
to
extrapolate
from
a
limited database
for
atmospheric
ap-
plications. Accurate measurements must
be
earned
out to
determine
the
rate constants
as a
function
of
temperature, pressure,
and the
third body
(in the
case
of
termolecular
reactions) over
the
range
of
conditions expected
in the
atmosphere under study.
3.6
Heterogeneous Reactions
Consider
an
atmosphere containing species
X and
aerosol
particles.
X can
collide with
and
stick
to the
aerosols:
X(ads) denotes
the
adsorbed species.
Let
n
a
and
r
a
be the
number density
and
radius
of
the
aerosols,
respectively.
The
rate
at
which
X is
adsorbed
is
with
the
unimolecular
rate
coefficient
given
by
where
v =
(8kT/jtm)i
is the
mean thermal speed
of X and
y
is the
accommodation
(or
sticking)
coefficient.
This formula
can
obviously
be
generalized
to a
distribution
of
aerosol particles
with
different
radii.
An
alternative
way to
write (3.67)
is

Chemical
Kinetics
73
where
A is the
area
of
aerosol
per
unit
volume.
The
most
difficult
quantity
to
determine
in
the
formulas
(3.67)
and
(3.68)
is the
dimensionless parameter
y.
We
give
an
example
of an
important heterogeneous reaction
in the
terrestrial stratosphere:
where
the
"aerosol"
may be a
H2SO4 particle
or an ice
particle.
The
values
of y are
of
the
order
10~
2
and
10~',
respectively,
for the
above
two
types
of
particles. Note
that
heterogeneous reactions
(3.69)
and
(3.70) turn
two
rather stable reservoir species
HC1
and
CIONO
2
into
C1
2
,
from
which reactive chlorine
is
readily
released.
A
famous
heterogeneous reaction
in
astrophysics
is the
formation
of
H
2
from
H
atoms
on the
surface
of
grains
in the
interstellar medium:
This
is
believed
to be the
principal pathway
for the
recombination
of H
atoms.
3.7
Miscellaneous Reactions
3.7.1
Reaction
with Excited
Species
Photolysis
and
chemical reactions
often
produce species that
are
vibrationally
or
elec-
tronically
excited.
These
species have more energy than their counterparts
in the
ground
state.
The
electronically excited
species
may
have
different
spin states that
facilitate
chemical reactions.
The
excited states
of
common molecules
are
listed
in
table
3.3.
The
theory
of
excited state reactions
is the
same
as
that
for the
ground state.
We
give examples
in the
following
paragraphs.
The
reaction
is
endothermic
by 41
kcal
mole""
1
,
and
hence
is not
important
in the
ionospheres
of
the
giant planets. However,
if the
H
2
molecules
are in
vibrationally excited states
with
v'
> 4,
then
this
reaction
is
exothermic
and is
expected
to be
fast.
Photolysis
of
CHt
produces methylene radicals
in the
ground state
(
3
CH
2
)
and
in
an
excited state
(
1
CH
2
),
the two
states being
isoelectronic
to
O(
3
P)
and
O(
1
D),
respectively.
The
reactivities
of the two
species
are
very
different.
For
example,
the
reaction
has
rate
coefficient
k = 1 x
10~
12
cm
3
s"
1
,
but the
corresponding reaction between
3
CH
2
and
H
2
is
negligible.
The
reaction

74
Photochemistry
of
Planetary Atmospheres
Table
3.3
Some
metastable excited
states
of
atoms
and
molecules"
Gound
state
H(
2
S)
C(
3
P)
CH
2
(X
3
B,)
0(
3
P)
N(
4
S)
0
2
(X
3
S-)
S0
2
(X'A,)
Excited
state
H(
2
S)
C('D)
C('S)
CH
2
(a'Ai)
0('D)
0('S)
N(
2
D)
N(
2
P)
0
2
(a'A
g
)
0
2
(b'£+)
S0
2
(a
3
B,)
Energy
(eV)
10.2
1.26
2.68
0.1-1
1.97
4.19
2.38
3.58
0.98
1.63
3.19
Radiative
lifetime
(s)
b
0.12
3.2(3)
2
—
110
0.74
9.4
12
2.7(3)
12
2.7(-3)
"Data
are from
Okabe
(1978).
b
The
notation
for
radiative lifetime a(b)
reads
ax
10*.
is
endothermic
by 17
kcal
mole
'
when
the
oxygen atom
is in the
ground
(
3
P)
state.
However,
if the O
atom
is in the first
excited state
('D),
the
reaction
is
exothermic
by
28.7 Kcal
mole""
1
and is
exceedingly rapid:
The
primary source
of
O('D)
in the
terrestrial atmosphere
is
photolysis
of
63:
The
bulk
of
O('D)
produced
in
(3.77)
is
quenched
to the
ground state
by
but
enough survives
to
drive
the
reaction (3.76)
and
make
it the
principal source
of
the
hydroxyl radical
in the
terrestrial troposphere
and
stratosphere.
3.7.2
Dissociative
Recombination
Reactions
We
pointed
out in
section 3.4.4 that ion-molecule reactions
are
generally faster than
neutral-neutral
reactions. Reactions between electrons
and
molecular ions such
as
are
extremely
fast,
with
rate
coefficients
of the
order
of
10~
6
to
10~
8
cm
3
s~'.
The
reasons
are the
strong Coulomb attraction between
an ion and an
electron,
and the
greater mobility
of the
electron.
We
give
a few
examples
of
this type
of
reaction that
are
important
in
planetary atmospheres:

Chemical Kinetics
75
where
the
units
for the
rate coefficients
are
cm
3
s~'
and the
rate
coefficient
for
(3.80)
refers
to
electron temperature
T
e
,
which
can be
higher than
the
neutral temperature
T in the
ionosphere.
The
fast
rates
of
dissociative
recombination
ultimately
limit
the
concentrations
of
molecular ions
in
planetary ionospheres.
3.7.3 Radiative
Association
Reactions
The
reaction between
an
electron
and an
atomic
ion of the
type
is
much slower than
(3.79),
because
the
excess
energy produced
in
(3.79)
can all be
carried away
in the
breaking
of the
A—B
bond
and the
kinetic energy
of the
fragments.
However,
in
reaction (3.83)
all the
excess energy associated with
the
capturing
the
electron
into
a
bound state must
be
radiated away,
a
relatively
inefficient
process
for
energy
loss.
Consequently,
the
rate coefficients
for
radiative
association
are
small,
of
the
order
of
10~'
2
cm
3
s""
1
,
as
shown
in the
following examples:
The
rate coefficients
are in
units
of
cm
3
s~'.
Note that
the
difference
between
the
rates
for
(3.79)
and
(3.83)
is five
orders
of
magnitude.
The
slow
rate
of
radiative association
is
the
main reason
for the
long lifetime
of
atomic ions
in the
upper ionospheres
of
Earth
and the
giant planets.
Neutral atoms
can
also
recombine
by
radiative association:
This
is
also
an
inefficient
process
and
requires
the
existence
of a
low-lying electronic
state that
can
radiate into
the
ground state.
We may
make
a
rough estimate
as
follows.
The
radiative association rate
coefficient
may be
computed
from
where
k
c
is the gas
kinetic rate
coefficient
(3.28)
and / is an
efficiency
factor that
measures
the
probability that
the
emission takes
place
during
the
encounter
period.
The
time
for a
potential curve crossing
is of the
order
of
10~
12
s. The
Einstein
coefficient
for
a
fast
radiative rate
is
10
8
s~'.
Therefore,
the
probability
of
emission
is
10~
4
.
This
would
yield
an
upper
limit
of
10~
14
cm
3
s~'
for
k
ra
.
The
actual rate coefficients
are
much
smaller,
as
shown
in the
following examples
