Yung Y.L., DeMore W.B. Photochemistry of Planetary Atmospheres
Подождите немного. Документ загружается.


56
Photochemistry
of
Planetary Atmospheres
2.
Bimolecular
reactions
3.
Termolecular
reactions
where
M
is a
third body,
the
concentration
of
which
is
that
of the
ambient atmosphere.
The
rates
of
reaction
(in
units
of
molecules
cm~
3
s~')
for
reactions
(3.1)-(3.3)
are
given,
respectively,
by
where
the
quantities
in
brackets denote concentrations
in
units
of
molecules
per
cm
3
,
and
k\,
&2>
and
£3
are
rate
coefficients
for first-order,
second-order,
and
third-order
reactions, respectively,
in
units
of
s"
1
,
cm
3
s"
1
,
and
cm
6
s"
1
.
The
rate coefficients
have
a
simple physical meaning. Consider
the
rate
of
loss
of
species
A due to
each
of
the
reactions
(3.1H3.3):
where
ai
=
ki,
a
2
=
MB],
and
«
3
=
£
3
[B][M].
Solving (3.7) yields
Therefore, species
A
will decay
to
e~
l
of its
initial value
in a
time interval equal
to
l/jfci,
l//t
2
[B],
and
1/£
3
[B][M]
due to
reactions (3.1),
(3.2),
and
(3.3),
respectively.
In
the
following
sections
we
discuss measurements
and
theories
of
rate coefficients.
In
general, rate
coefficients
are
complex
functions
of
pressure
and
temperature
and are
measured
in the
laboratory. Only
the
simplest reaction
coefficients
have been computed
successfully.
Nevertheless,
the
theoretical ideas
are
important
for
understanding
the
order
of
magnitude
of
rate coefficients
and
certain regularities
in
their behavior.
3.2
Thermochemical
Reactions
Chemical
reactions involve exchange
of
energy
as
well
as
exchange
of
mass.
A
con-
venient
measure
of the
energy content
of a
molecule
is the
enthalpy
of
formation,
H.
The
enthalpy
of the
most stable
form
of the
elements
is
usually taken
as
zero.
For
example,
the
enthalpy
of H2 is
zero; that
for H is
52.1
kcal
mole"
1
.
The
enthalpy
change
in the
reaction

Chemical
Kinetics
57
is
104.2
kcal
mole"
1
.
This
is the
amount
of
energy required
to
break
the H-H
bond.
Since average collisional energies
are
much smaller
in
most atmospheres, reaction
(3.9) will
not
occur
at a
significant
rate.
The
reverse
of
(3.9),
releases
energy
and can
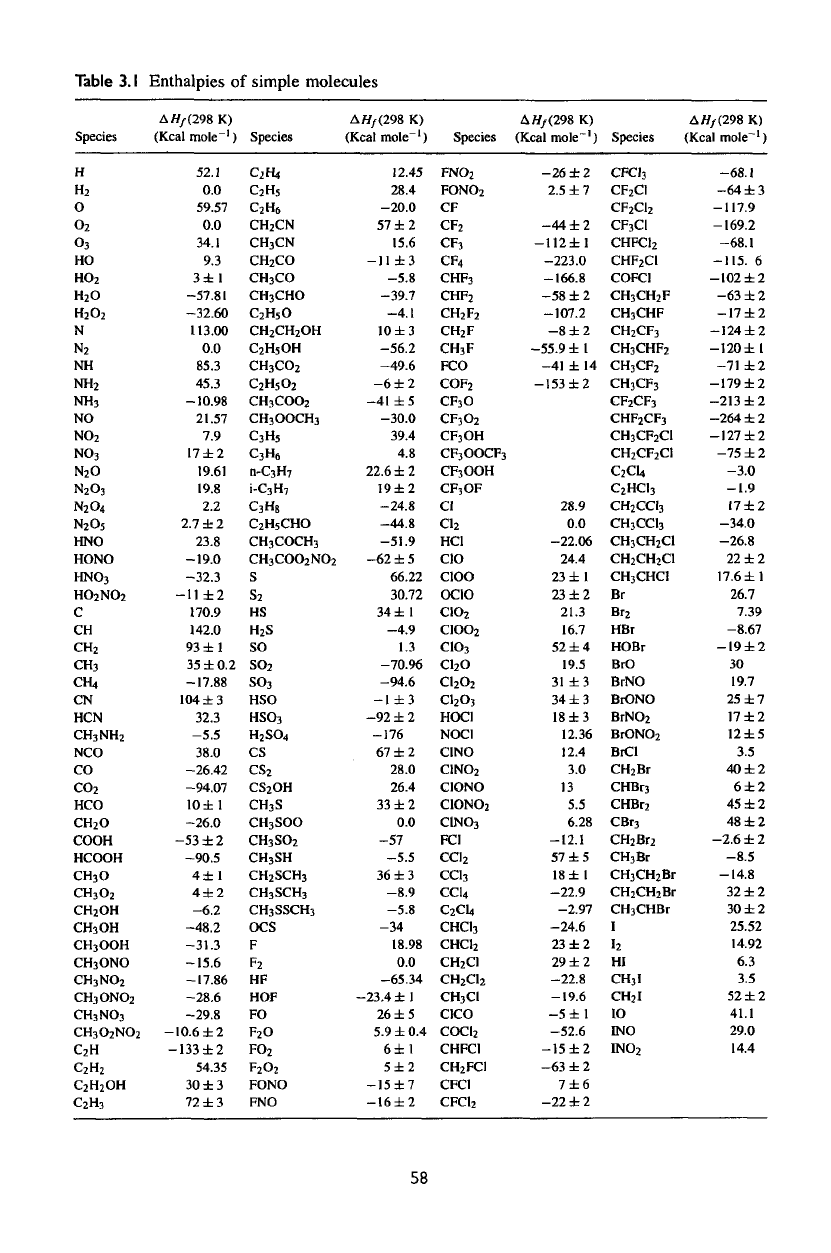
proceed spontaneously. Table
3.1
gives enthalpies
of
formation
for
molecules
of
interest
in
planetary atmospheres.
The
thermodynamic
properties
strongly
influence
the
reactivity
of
molecules. Molecules such
as N2, H2, and
CH/t
have
low
values
of
enthalpy
and are
thermally stable. Radicals such
as O, H, and
Cl
have
high values
of
enthalpy
and are
extremely reactive.
Reaction
(3.10)
proceeds spontaneously
to the
right because
of the
natural tendency
of
a
system
to
move toward
a
state
of
lower energy. Indeed,
in a
static state
the
laws
of
mechanics require that
the
physical system
be in a
state
of
minimum energy. How-
ever,
in a
dynamical system
with
many
gas
molecules, there
is
another fundamental
principle,
the
principle
of
maximum entropy,
or the
tendency
for a
system
to
reach
maximum
disorder.
Thus,
each
molecule
is
characterized
by a
thermodynamic
quantity
known
as
entropy (S), which
is a
measure
of the
number
of
states
available
to it. By
the
laws
of
probability,
the
configurations with more states
are
favored.
The
entropies
(5)
of
simple molecules
are
listed
in
table 3.2. Referring
to
reaction
(3.9),
the
entropy
on
the
left
side
is
31.2
cal
mole"
1
K"
1
and on the
right side
is 2 x
27.39
=
54.8
cal
mole"
1
K
-1
.
Thus, according
to the
maximum entropy principle, (3.9) will
proceed
so as to
increase
the
entropy
of the
system
by
23.6
cal
mole"
1
K"
1
.
Physically,
2
moles
of H
atoms represent more disorder
than
1
mole
of
Ha
and in the
absence
of
the
energy principle (3.9) would prevail.
The
combination
of
these
two
principles
is
formulated
in
terms
of
Gibbs free
energy:
where
T is
temperature.
For a
closed thermodynamic system,
the
equilibrium state
is
attained when
G is a
minimum.
This
is
analogous
to a
mechanical
system,
which
seeks minimum potential energy. Note that both
the
minimum energy principle
and the
maximum
entropy principle
are
incorporated
as
special
cases
of the
Gibbs principle.
As
an
application
of the
Gibbs principle, consider
the
change
in G in
(3.9).
At 300
K
(representative
of
planetary atmospheres)
the
change
in G
from
the
left
side
to the
right
side
is
97.1 kcal
mole"
1
.
Therefore, equilibrium favors
the
molecular form,
Ha.
However,
at
6000
K
(representative
of the
solar atmosphere),
the
change
in
Gibbs
free
energy
is
—37.4
kcal
mole"
1
(for simplicity
we use the
enthalpies
and
entropies
at 300
K).
Equilibrium
is now
shifted
to the
right. This explains
why
Ha
is the
more stable
form
of
hydrogen
in
planets, whereas
in the
solar atmosphere
H
atoms dominate over
H
2
.
Referring
to the
definition
of G in
(3.11),
the
energy term
H is
more important
than
the
entropy term
TS
at 300 K, but the
reverse
is
true
at
6000
K.
Note
that
enthalpy
is a
measure
of the
energy involved
in
making
or
breaking chemical
bonds—
an
internal energy that
depends,
to first
order,
on the
electronic
configurations
of the
molecules
and is
largely independent
of
external parameters. Conversely,
the
entropy
part
of G is
proportional
to
temperature,
which
is a
macroscopic property
of the
gas.
The
Gibbs principle provides
a
beautiful
and
simple connection between
the
micro-
Table
3.1
Enthalpies
of
simple molecules
Species
H
H
2
O
0
2
0
3
HO
HO
2
H
2
O
H
2
0
2
N
N
2
NH
NH
2
NH
3
NO
N0
2
N0
3
N
2
O
N
2
0
3
N
2
0
4
N
2
0
5
HNO
HONO
HN0
3
HO
2
NO
2
C
CH
CH
2
CH
3
CH,
CN
HCN
CH
3
NH
2
NCO
CO
C0
2
HCO
CH
2
O
COOH
HCOOH
CH
3
O
CH
3
0
2
CH
2
OH
CH
3
OH
CH
3
OOH
CH
3
ONO
CH
3
N0
2
CH
3
ON0
2
CH
3
N0
3
CH
3
0
2
N0
2
C
2
H
C
2
H
2
C
2
H
2
OH
C
2
H
3
AH/
(298
K)
(Kcal
mole"
1
)
52.1
0.0
59.57
0.0
34.1
9.3
3± 1
-57.81
-32.60
113.00
0.0
85.3
45.3
-10.98
21.57
7.9
17±2
19.61
19.8
2.2
2.7
±2
23.8
-19.0
-32.3
-11 ±2
170.9
142.0
93
±1
35
±0.2
-17.88
104
±3
32.3
-5.5
38.0
-26.42
-94.07
10
±1
-26.0
-53 ±2
-90.5
4± 1
4±2
-6.2
-48.2
-31.3
-15.6
-17.86
-28.6
-29.8
-10.6
±2
-133±2
54.35
30
±3
72
±3
AH/(298
K)
Species (Kcal
mole"
1
)
C
2
H4
C
2
H
5
C
2
H
6
CH
2
CN
CH
3
CN
CH
2
CO
CH
3
CO
CH
3
CHO
C
2
H
5
0
CH
2
CH
2
OH
C
2
H
5
OH
CH
3
C0
2
C
2
H
5
0
2
CH
3
COO
2
CH
3
OOCH
3
C
3
H
5
C
3
H
6
n-C
3
H
7
i-C
3
H
7
C
3
H
8
C
2
H
5
CHO
CH
3
COCH
3
CH
3
COO
2
NO
2
s
S
2
HS
H
2
S
SO
S0
2
S0
3
HSO
HSO
3
H
2
S0
4
CS
CS
2
CS
2
OH
CH
3
S
CH
3
SOO
CH
3
SO
2
CH
3
SH
CH
2
SCH
3
CH
3
SCH
3
CH
3
SSCH
3
OCS
F
F
2
HF
HOP
FO
F
2
0
F0
2
F
2
0
2
FONO
FNO
12.45
28.4
-20.0
57
±2
15.6
-11±3
-5.8
-39.7
-4.1
10
±3
-56.2
-49.6
-6 ±2
-41
±5
-30.0
39.4
4.8
22.6
±2
I9±2
-24.8
-44.8
-51.9
-62 ±5
66.22
30.72
34
±1
-4.9
1.3
-70.96
-94.6
-1±3
-92 ±2
-176
67
±2
28.0
26.4
33
±2
0.0
-57
-5.5
36
±3
-8.9
-5.8
-34
18.98
0.0
-65.34
-23.4
± 1
26
±5
5.9
±0.4
6±1
5±2
-15±7
-16±2
Atf/(298
K)
Species
(Kcal
mole"
1
)
FNO
2
FONO
2
CF
CF
2
CF
3
CF
4
CHF
3
CHF
2
CH
2
F
2
CH
2
F
CH
3
F
FCO
COF
2
CF
3
0
CF
3
0
2
CF
3
OH
CF
3
OOCF
3
CF
3
OOH
CF
3
OF
Cl
C1
2
HC1
CIO
C1OO
OC1O
C10
2
C1OO
2
C1O
3
C1
2
0
C1
2
0
2
C1
2
0
3
HOC1
NOC1
C1NO
C1N0
2
C1ONO
C1ONO
2
C1N0
3
FC1
CC1
2
CC1
3
CC1
4
C
2
CU
CHC1
3
CHC1
2
CH
2
C1
CH
2
C1
2
CH
3
CI
C1CO
COCI
2
CHFC1
CH
2
FC1
CFC1
CFC1
2
-26 ±2
2.5
±7
-44 ±2
-112±1
-223.0
-166.8
-58 ±2
-107.2
-8 ±2
-55.9
± 1
-41 ± 14
-153±2
28.9
0.0
-22.06
24.4
23
± 1
23
±2
21.3
16.7
52
±4
19.5
31
±3
34
±3
18±3
12.36
12.4
3.0
13
5.5
6.28
-12.1
57
±5
18± 1
-22.9
-2.97
-24.6
23
±2
29
±2
-22.8
-19.6
-5±
1
-52.6
-15±2
-63 ± 2
7±6
-22 ±2
A///
(298
K)
Species
(Kcal
mole~')
CFC1
3
CF
2
C1
CF
2
C1
2
CF
3
C1
CHFC1
2
CHF
2
C1
COFC1
CH
3
CH
2
F
CH
3
CHF
CH
2
CF
3
CH
3
CHF
2
CH
3
CF
2
CH
3
CF
3
CF
2
CF
3
CHF
2
CF
3
CH
3
CF
2
C1
CH
2
CF
2
C1
C
2
CU
C
2
HC1
3
CH
2
CC1
3
CH
3
CC1
3
CH
3
CH
2
C1
CH
2
CH
2
C1
CH
3
CHC1
Br
Br
2
HBr
HOBr
BrO
BrNO
BrONO
BrN0
2
BrON0
2
BiCl
CH
2
Br
CHBr
3
CHBr
2
CBr
3
CH
2
Br
2
CH
3
Br
CH
3
CH
2
Br
CH
2
CH
2
Br
CH
3
CHBr
I
h
HI
CH
3
I
CH
2
I
1O
INO
IN0
2
-68.1
-64 ±3
-117.9
-169.2
-68.1
-115.
6
-102
±2
-63 ±2
-17±2
-124
±2
-120±
1
-71 ±2
-179
±2
-213
±2
-264
± 2
-127±2
-75 ±2
-3.0
-1.9
I7±2
-34.0
-26.8
22
±2
17.6
±1
26.7
7.39
-8.67
-19±2
30
19.7
25
±7
17±2
12±5
3.5
40±2
6±2
45
±2
48
±2
-2.6
± 2
-8.5
-14.8
32
±2
30
±2
25.52
14.92
6.3
3.5
52
±2
41.1
29.0
14.4
58

Table
3.2
Entropies
of
simple molecules
Species
H
H
2
0
0
2
0
3
HO
H0
2
H
2
O
H
2
0
2
N
N
2
NH
NH
2
NH
3
NO
NO
2
NO
3
N
2
O
N
2
0
3
N
2
0
4
N
2
0
5
HNO
HONO
HNO
3
H0
2
NO
2
C
CH
CH
2
CH
3
CR,
CN
HCN
CH
3
NH
2
NCO
CO
C0
2
HCO
CH
2
0
COOH
HCOOH
CH
3
O
CH
3
0
2
CH
2
OH
CH
3
OH
CH
3
OOH
CH
3
ONO
CH
3
NO
2
CH
3
ON0
2
CH
3
NO
3
CH
3
0
2
N0
2
C
2
H
C
2
H
2
C
2
H
2
OH
C
2
H
3
5°(298
K)
(cal~'
mole"
1
cleg-')
27.4
31.2
38.5
49.0
57.0
43.9
54.4
45.1
55.6
36.6
45.8
43.3
46.5
46.0
50.3
57.3
60.3
52.6
73.9
72.7
82.8
52.7
59.6
63.7
37.8
43.7
46.3
46.4
44.5
48.4
48.2
58.0
55.5
47.3
51.1
53.7
52.3
61.0
59.4
55.0
65.3
58.8
57.3
67.5
68.0
65.7
72.1
76.1
49.6
48.0
56.3
Species
C
2
H4
C
2
H
5
C
2
H<i
CH
2
CN
CH
3
CN
CH
2
CO
CH
3
CO
CH
3
CHO
C
2
H
5
0
CH
2
CH
2
OH
C
2
H
S
OH
CH
3
CO
2
C
2
H
5
0
2
CH
3
COO
2
CH
3
OOCH
3
C
3
H
5
C
3
H
6
n-C
3
H
7
i-C
3
H
7
C
3
H
8
C
2
H
5
CHO
CH
3
COCH
3
CH
3
COO
2
NO
2
S
S
2
HS
H
2
S
SO
SO
2
SO
3
HSO
HS0
3
H
2
SO
4
CS
CS
2
CS
2
OH
CH
3
S
CH
3
SOO
CH
3
SO
2
CH
3
SH
CH
2
SCH
3
CH
3
SCH
3
CH
3
SSCH
3
OCS
F
F
2
HF
HOP
FO
F
2
0
F0
2
F
2
0
2
FONO
FNO
5°(298
K)
(car
1
mole-'
deg-
1
)
52.5
58.0
54.9
58.0
58.2
57.8
64.5
63.2
65.3
67.5
75.0
74.1
62.1
63.8
68.5
66.7
64.5
72.8
70.5
40.1
54.5
46.7
49.2
53.0
59.3
61.3
69.1
50.3
56.9
57.6
61.0
68.4
80.5
55.3
37.9
48.5
41.5
54.2
51.8
59.1
61.9
66.3
62.2
59.3
Species
FNO
2
FON0
2
CF
CF
2
CF
3
CF
4
CHF
3
CHF
2
CH
2
F
2
CH
2
F
CH
3
F
FCO
COF
2
CF
3
O
CF
3
0
2
CF
3
OH
CF
3
OOCF
3
CF
3
OOH
CF
3
OF
Cl
C1
2
HC1
CIO
C1OO
OCIO
C10
2
C10O
2
C1O
3
C1
2
0
C1
2
0
2
C1
2
0
3
HOC1
NOC1
C1NO
C1N0
2
C10NO
ClONOj
C1N0
3
FC1
CC1
2
CC1
3
ecu
C
2
CL,
CHC1
3
CHC1
2
CH
2
C1
CH
2
C1
2
CH
3
CI
C1CO
COC1
2
CHFC1
CH
2
FC1
CFC1
CFC1
2
S°
(298
K.)
(cal"
1
mole"
1
deg-
1
)
62.3
70.0
50.9
57.5
63.3
62.4
62.0
61.7
58.9
55.9
53.3
59.4
61.9
77.1
39.5
53.3
44.6
54.1
64.0
61.5
63.0
73.0
67.0
64.0
72.2
56.5
62.5
62.5
65.1
52.1
63.4
71.0
81.4
70.7
66.5
58.2
64.6
56.1
63.3
67.8
63.3
62.0
71.5
Species
CFC1
3
CF
2
C1
CF
2
C1
2
CF
3
C1
CHFC1
2
CHF
2
C1
COFC1
CH
3
CH
2
F
CH
3
CHF
CH
2
CF
3
CH
3
CHF
2
CH
3
CF
2
CH
3
CF
3
CF
2
CF
3
CHF
2
CF
3
CH
3
CF
2
C1
CH
2
CF
2
C1
C
2
CU
C
2
HC1
3
CH
2
CC1
3
CH
3
CC1
3
CH
3
CH
2
CI
CH
2
CH
2
C1
CH
3
CHCI
Br
Br
2
HBr
HOBr
BrO
BrNO
BrONO
BrN0
2
BrONO
2
BrCI
CH
2
Br
CHBr
3
CHBr
2
CBr
3
CH
2
Br
2
CH
3
Br
CH
3
CH
2
Br
CH
2
CH
2
Br
CH
3
CHBr
I
h
HI
CH
3
I
CH
2
I
IO
INO
IN0
2
5°
(298
K)
(car
1
mole-'
deg-
1
)
74.0
68.7
71.8
68.3
70.1
67.2
66.2
63.3
71.8
67.6
69.9
68.6
81.6
68.7
81.4
77.5
80.6
76.4
65.9
41.8
58.6
47.4
59.2
56.8
65.3
57.3
79.1
80.0
70.1
58.7
68.6
43.2
62.3
49.3
60.6
58.8
67.6
70.3
59

60
Photochemistry
of
Planetary
Atmospheres
scopic properties
of the
individual molecules
and the
macroscopic properties
of the gas
as
a
whole.
Consider
a
general chemical reaction,
with
rate
coefficient
kf.
Note that
by
appropriate
choice
of the
values
m/
and
n,
(including
zero)
we
have
all
reactions
of
types
(3.1)-(3.3).
All our
arguments
can
obviously
be
extended
to
reactions involving more than three
species.
The
reverse
of
reaction
(3.12)
is
with
rate
coefficient
k
r
.
For a
closed chemical system that
has
reached equilibrium,
the
forward
and the
backward reaction rates must
be
equal:
Rearranging
(3.14)
we
have
It
can be
shown that ratio (3.15)
can be
expressed
as a
function
of the
Gibbs free
energies:
where
R is the
molar
gas
constant
and
Although
the
Gibbs
free
energy gives
no
direct prediction
of the
values
of
individual
rate coefficients,
the
ratio
of the
forward
and the
reverse rate coefficients
can
always
be
computed using Gibbs free energies. This
is an
important result because
it is
often
hard
to
measure both
kf and
k
r
.
By
(3.16)
we
only have
to
measure
one and can
obtain
the
other using
thermodynamic
considerations.
It can be
shown that
for a
system that
has
reached equilibrium,
the
partitioning
of
the
species
is
such that
the
total Gibbs
free
energy
of the
system
is a
minimum.
Note that
the
thermodynamic properties
of the
molecules
now
completely determine
the
chemical composition
of the
system without
any
reference
to the
rate coefficients.
As an
example
of
thermoequilibrium
chemistry, consider
a
parcel
of air
containing
N
2
and
O
2
,
heated
up to
thousands
of
degrees,
as in a
lightning bolt
or the
combustion
chamber
of an
automobile.
The
reaction
repartitions
the
nitrogen
and
oxygen atoms into
the
molecules
N
2
,
O
2
,
and NO. The
composition
of the air
parcel
is
uniquely determined
by
specifying
the
initial partial
pressures
of
N
2
and
O
2
and the final
temperature
of the
parcel.

Chemical
Kinetics
61
There
is one
great deficiency
in
this
thermodynamic
scheme. Thermodynamics
offers
no
clue
to the
time constant that
is
needed
for the
equilibrium
to be
reached.
For
instance,
in
reaction (3.19)
we do not
know whether
the
equilibrium concentrations
are
attained.
We do not
know,
as the air
parcel cools down,
at
what temperature
the
parcel
is
"quenched"
so
that
its
composition will
not
undergo
further
change
with
lowering temperature.
For
this
we
need
the
kinetic information,
discussed
in the
following
sections.
3.3
Unimolecular
Reactions
Once
a
chemical bond
is
formed,
it is
generally
difficult
to
break.
The
rate
coefficient
for
the
spontaneous decomposition
of A
into products
B and C by
(3.1)
is
where
k is the
Boltzmann constant,
h is the
Planck constant,
and AG =
G(B)
+
G(C)
—
G(A).
At
room temperature
the
preexponential factor
is of the
order
10
13
s"
1
(~molecular
vibrational frequency).
For
stable molecules
we
often
have
AG
»
RT,
and
the
exponential factor tends
to
make
k\
very small.
By
far the
most important
first-order
(unimolecular)
processes
in the
atmosphere
are
ones that
are
excited
by the
absorption
of a
photon,
as
discussed
in
chapter
2:
followed
by
The
second
step
is now
fast
because
the
bond energy barrier
has
been overcome
by the
absorption
of a
photon.
The
rate-limiting step
is
(3.21).
Hence,
for
most applications,
we
have
where
J is the
photodissociation
coefficient
defined
by
(2.9)
for
species
A.
Process (3.21) usually occurs with
the
absorption
of a
single ultraviolet photon
with
sufficient
energy
to
break
the
chemical bond
of A.
There
is
another
process
using
multiphoton
absorption
in the
infrared.
The
molecule
is
pumped
to the
dissociation
continuum
via
multiphoton excitation
of the
vibrational levels. However, this
can
only
be
done using
a
laser
in the
laboratory,
and is
unimportant
in the
atmosphere.
3.4
Bimolecular
Reactions
3.4.1
Molecular
Collisions
Consider
the
bimolecular reaction (3.2). Molecules
A and B
have
to
collide
with
each
other
before they
can
react.
For
simplicity
let us
assume that molecules
A and B are

62
Photochemistry
of
Planetary
Atmospheres
spheres
with
masses
/MA
and
»JB,
respectively,
and
have radii
r\
and
TB,
respectively.
The
cross section
for a
binary collision
is
The
number
of
binary collisions
cm~
3
s"
1
is
given
by
(3.5) with
where
/
represents
the
normalized distributions
for
molecular velocities
and
w
=
|t>A
—
VB\.
For a gas in
equilibrium
at
temperature
T,
the
velocity
distribution
is
given
by
the
Maxwell-Boltzmann distribution.
In
this
case
the
double integral
in
(3.25)
may
be
evaluated
to
yield
where
the
mean speed
v
r
is
given
by
Note that
v
r
is
just
the
mean
speed
of a
particle
in
thermal equilibrium
at
temperature
T
with reduced mass
(j,
=
m^mB/(m^
+ OTB). We may
evaluate
k
c
for the
major
molecules
in the
terrestrial atmosphere.
The
cross
section
for
collision
is
about
5 x
10~
15
cm
2
;
v
r
at 300 K is
about
4 x
10
4
cm
s"
1
.
Hence,
the gas
kinetic rate coefficient
is
approximately
Since
the
rate
of
chemical reactions normally cannot
exceed
that
of
kinetic collisions,
the
value
of
k
c
given
by
(3.28)
must
be the
upper limit
for the
rate coefficient
of
binary
reactions between neutral molecules. Ions
can
react
via the
long-ranged Coulomb force
and
are not
subjected
to the
limitation
of
(3.28).
(See discussion
in
section
3.4.3.)
There
are a
number
of
reactions whose rate coefficients
do
approach that
of
(3.28):
where
the
units
for the
rate coefficients
are
cm
3
s~'.
Unfortunately, this collisional
theory
is too
simplistic
to
account
for the
detailed
molecular
interactions
involved
in
a
chemical reaction.
In
sections
3.4.2-3.4.4,
we
present more realistic theories
of
chemical kinetics.

Chemical
Kinetics
63
3.4.2
Forming
Chemical
Bonds
In
the
previous section
we
obtained
the
kinetic collision rate,
without
further
regard
for
the
internal
structure
of
each molecule.
How
effective
is
each collision
at
inducing
a
chemical reaction, that
is,
forming
a new
chemical bond?
To
answer this question
we
need detailed quantum mechanical knowledge
of the
reactants
and the
products.
(The discussion here
is
based
on
unpublished material
by G.
Blake.)
Consider
two
atoms
A and B
undergoing
a
collision
to
form
a
stable molecule
AB.
In
section
3.3 we
studied
the
unimolecular
dissociation
of a
stable molecule.
The
breaking
of a
chemical bond
is
difficult
because
a
minimum
amount
of
energy
(the
bond energy) must
be
supplied
to the
molecule
in
appropriate form.
The
reverse
process,
the
forming
of a new
bond,
is
also
difficult.
The
bond energy (Do)
is of the
order
of 5 eV,
which must
be
removed
in the
brief interval
of
time during collision.
The
size
of a
molecule
(d) is of the
order
of 5 A, and at
thermal velocity
v = 3 x
10
4
cm
s~
l
,
the
"collision
time"
is
about
2 x
10~
12
s. The
power
density
of
dissipation
is
vDo/d
3
,
or
about
10
8
W
cm~
2
.
It is
difficult
to
remove energy
at
this rate. Hence,
in
general,
the
transient
molecule
AB
would
not be
stabilized
but
would
fly
apart
as
A
and B.
The
formation
of a new
chemical bond
from
atoms
is an
inefficient
process,
as
shown
above.
There
are
three mechanisms
for
removing
the
excess energy
from the
newly
formed molecule:
(a)
termolecular
reaction,
using
collisions with
a
third body;
(b)
radiative association, radiating
the
energy away;
and (c)
heterogeneous reaction,
using
a
surface
to
absorb
the
energy.
These
processes
are
discussed
in
detail
in
sections
3.5, 3.7.3,
and
3.6, respectively.
3.4.3
Transition
State
Theory
While
it is
difficult
in the
atmosphere
to
create
or
break
a
chemical bond,
it is
relatively
easy
to
exchange chemical bonds.
For
example,
in a
metathetical reaction such
as
there
is a
preexisting chemical bond,
B—C,
and a new
bond,
A—B,
is
formed.
The
excess energy
from
the
bond formation
is
dissipated
in the
breaking
of the old
B—C
bond,
and the
overall reaction
exothermicity
can be
taken
up as
relative translational
energy
of the
products. Thus,
the
original
B—C
bond
is
exchanged
for the new
A—B
bond.
This type
of
reaction makes
up the
bulk
of
chemical reactions
in the
atmosphere.
We
now
examine (3.32)
in
more detail.
The first
step
is the
formation
of a
transient
triatomic
complex, known
as the
activated complex
or
transition
state:
There
are two
possible
fates
for the
transition state.
One
choice
is
going back
to the
reactants:
64
Photochemistry
of
Planetary Atmospheres
(a)
(b)
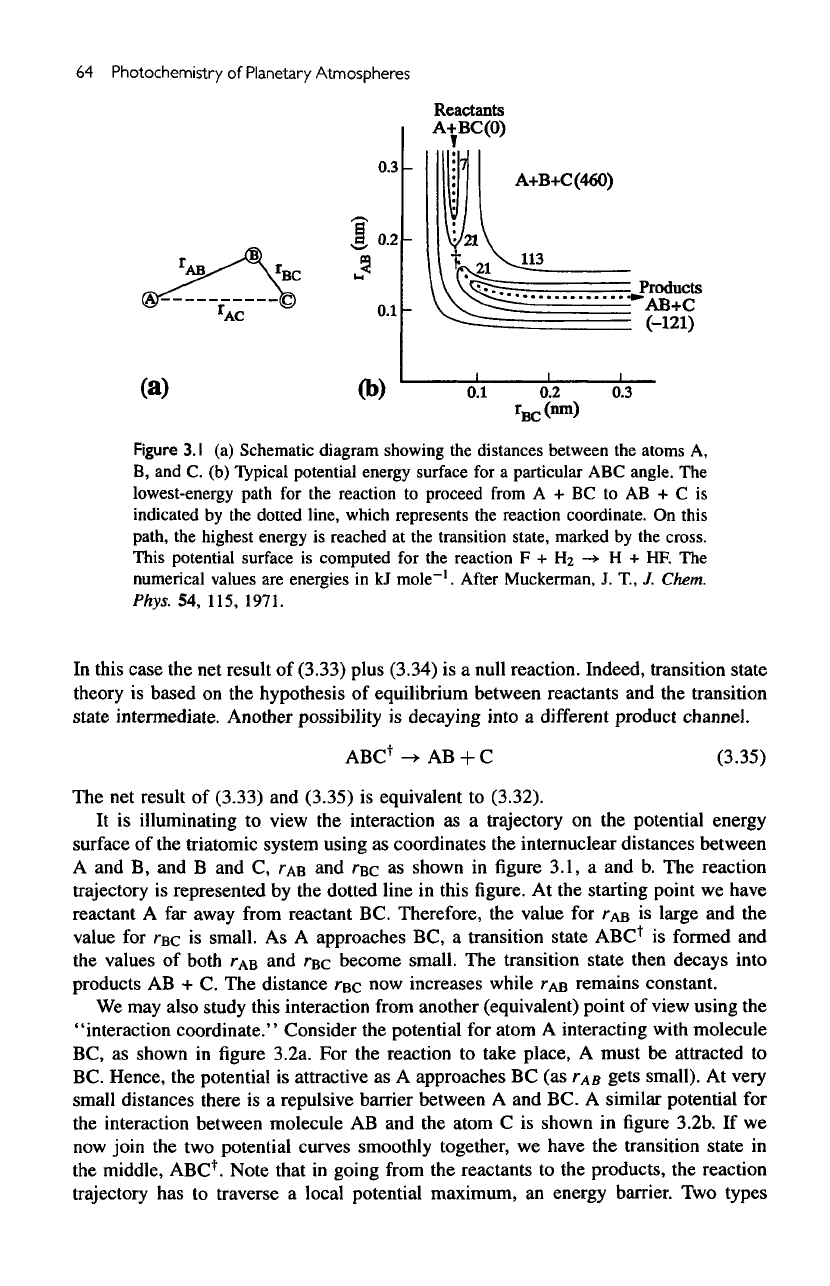
Figure
3.1
(a)
Schematic
diagram
showing
the
distances between
the
atoms
A,
B,
and C. (b)
Typical potential energy
surface
for a
particular
ABC
angle.
The
lowest-energy
path
for the
reaction
to
proceed
from
A + BC to AB + C is
indicated
by the
dotted
line,
which
represents
the
reaction coordinate.
On
this
path,
the
highest
energy
is
reached
at the
transition
state,
marked
by the
cross.
This
potential
surface
is
computed
for the
reaction
F +
Ha
->
H + HF. The
numerical
values
are
energies
in kJ
mole"
1
.
After
Muckerman,
J. T., J.
Chem.
Phys.
54,
115, 1971.
In
this
case
the net
result
of
(3.33)
plus
(3.34)
is a
null reaction. Indeed, transition state
theory
is
based
on the
hypothesis
of
equilibrium between reactants
and the
transition
state
intermediate.
Another
possibility
is
decaying into
a
different
product
channel.
The net
result
of
(3.33)
and
(3.35)
is
equivalent
to
(3.32).
It
is
illuminating
to
view
the
interaction
as a
trajectory
on the
potential energy
surface
of the
triatomic system using
as
coordinates
the
internuclear
distances between
A
and B, and B and C,
TAB
and
rsc
as
shown
in figure
3.1,
a and b. The
reaction
trajectory
is
represented
by the
dotted line
in
this
figure. At the
starting point
we
have
reactant
A far
away from reactant
BC.
Therefore,
the
value
for
TAB
is
large
and the
value
for
rac
is
small.
As A
approaches
BC, a
transition state
ABC*
is
formed
and
the
values
of
both
r
A
B
and
r^c
become small.
The
transition state then decays into
products
AB + C. The
distance
TBC
now
increases while
TAB
remains constant.
We
may
also study this interaction from another (equivalent) point
of
view using
the
"interaction
coordinate."
Consider
the
potential
for
atom
A
interacting with molecule
BC, as
shown
in figure
3.2a.
For the
reaction
to
take
place,
A
must
be
attracted
to
BC.
Hence,
the
potential
is
attractive
as A
approaches
BC (as
r^s
gets
small).
At
very
small
distances there
is a
repulsive barrier between
A and BC. A
similar potential
for
the
interaction between molecule
AB and the
atom
C is
shown
in figure
3.2b.
If we
now
join
the two
potential curves smoothly together,
we
have
the
transition state
in
the
middle,
ABC
f
.
Note that
in
going
from
the
reactants
to the
products,
the
reaction
trajectory
has to
traverse
a
local potential maximum,
an
energy barrier.
Two
types

Chemical
Kinetics
65
Figure
3.2 (a)
Schematic diagram
showing
the
attractive potentials
for
A
+ BC and AB + C. (b)
Schematic diagram
of the
potential
surface
along
the
reaction
coordinate
of figure
3.1b
(dotted
line)
for the
reaction
A + BC
->•
AB
+ C.
Based
on
unpublished
material
by G.
Blake.
of
situations
can
arise.
In the first
case,
as
shown
in figure
3.3,
the
potential energy
of
reactants
A + BC is
lower than
the
transition state
ABC*.
Even though
the net
reaction
from
A + BC to AB + C is
exothermic,
an
extra amount
of
energy, known
as
the
activation energy
(E
a
),
must
be
supplied
to
overcome
the
barrier.
The
bimolecular
rate
coefficient
&
2
may now be
expressed
by the
Arrhenius
expression:
where
A is the gas
kinetic rate coefficient
k
c
given
in
(3.28),
and the
exponential
function
takes into account
of the
activation energy.
It is
usual
to
measure
ki
em-
pirically
at
various temperatures
and
determine
E
a
empirically
from
the
data.
The
temperature
dependence
of A is
weak compared
with
the
exponential factor,
and A
may
be
regarded
as a
constant.
In the
second case,
as
shown
by the
reverse reaction
in
figure
3.3,
the
energy barrier
is
E
a
+
A//.
The
transition state theory predicts more than
the
empirical formula
(3.36).
By
assuming
quasiequilibrium between
the
reactants
and the
transition state,
the
theory
predicts
a
rate
coefficient
given
by
where
h is
Planck's constant,
Q
is the
partition
function,
and
E
a
is the
difference
in
the
enthalpies
of the
reaction. Note that
the
ratio
of the
partition
functions
in
(3.37)
is
the
equilibrium constant
for the
formation
of the
transition state.
In
applying formula
(3.37),
we
usually know
Q(A)
and
g(B).
Computation
of
f^ABC*)
requires knowl-
edge
of the
structure
of the
transition state
(e.g.,
whether
it is
linear, bent,
or
cyclic)
