Yung Y.L., DeMore W.B. Photochemistry of Planetary Atmospheres
Подождите немного. Документ загружается.


Figure
2.14
Potential energy diagram
for
Oz.
After
Gilmore (1971),
as
quoted
in
Steinfeld,
J.
I.,
1979,
Molecules
and
Radiation:
An
Intro-
duction
to
Modern Molecular
Spectroscopy
(Cambridge, Mass.:
MIT
Press).
36
Solar
Flux
and
Molecular
Absorption
37
(a)
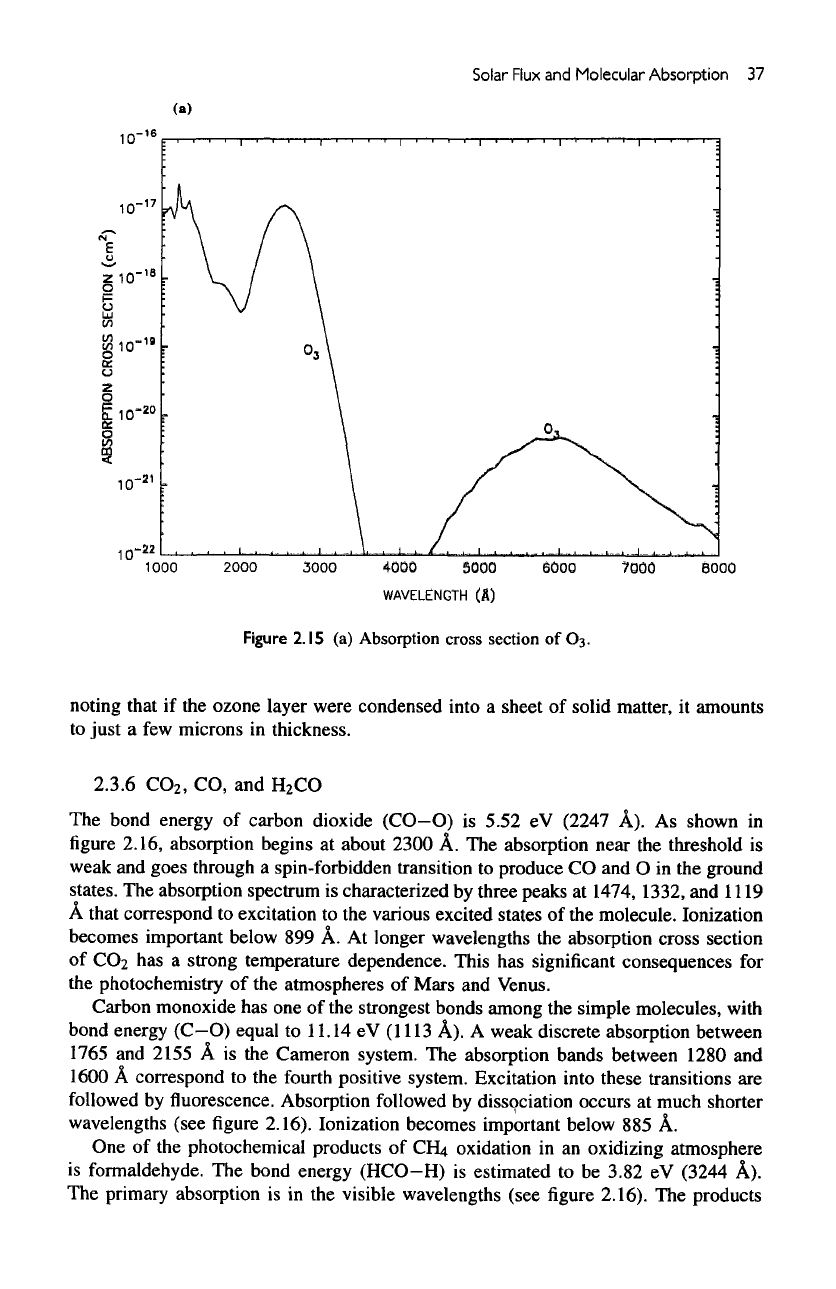
Figure
2.15
(a)
Absorption cross section
of 03.
noting
that
if the
ozone layer were condensed into
a
sheet
of
solid matter,
it
amounts
to
just
a few
microns
in
thickness.
2.3.6
CO
2
,
CO,
and
H
2
CO
The
bond energy
of
carbon dioxide
(CO-O)
is
5.52
eV
(2247
A). As
shown
in
figure
2.16, absorption begins
at
about
2300
A. The
absorption near
the
threshold
is
weak
and
goes through
a
spin-forbidden transition
to
produce
CO and O in the
ground
states.
The
absorption spectrum
is
characterized
by
three peaks
at
1474,
1332,
and
1119
A
that correspond
to
excitation
to the
various excited states
of the
molecule.
lonization
becomes important below
899 A. At
longer wavelengths
the
absorption
cross
section
of
CO
2
has a
strong temperature dependence. This
has
significant consequences
for
the
photochemistry
of the
atmospheres
of
Mars
and
Venus.
Carbon monoxide
has one of the
strongest bonds among
the
simple molecules,
with
bond
energy
(C-O)
equal
to
11.14
eV
(1113
A). A
weak discrete absorption between
1765
and
2155
A is the
Cameron system.
The
absorption bands between
1280
and
1600
A
correspond
to the
fourth
positive system. Excitation into these transitions
are
followed
by
fluorescence. Absorption followed
by
dissociation occurs
at
much shorter
wavelengths
(see
figure
2.16). lonization becomes important below
885 A.
One of the
photochemical products
of
CHj
oxidation
in an
oxidizing atmosphere
is
formaldehyde.
The
bond energy
(HCO-H)
is
estimated
to be
3.82
eV
(3244
A).
The
primary absorption
is in the
visible wavelengths
(see
figure
2.16).
The
products
38
Photochemistry
of
Planetary
Atmospheres
(b)
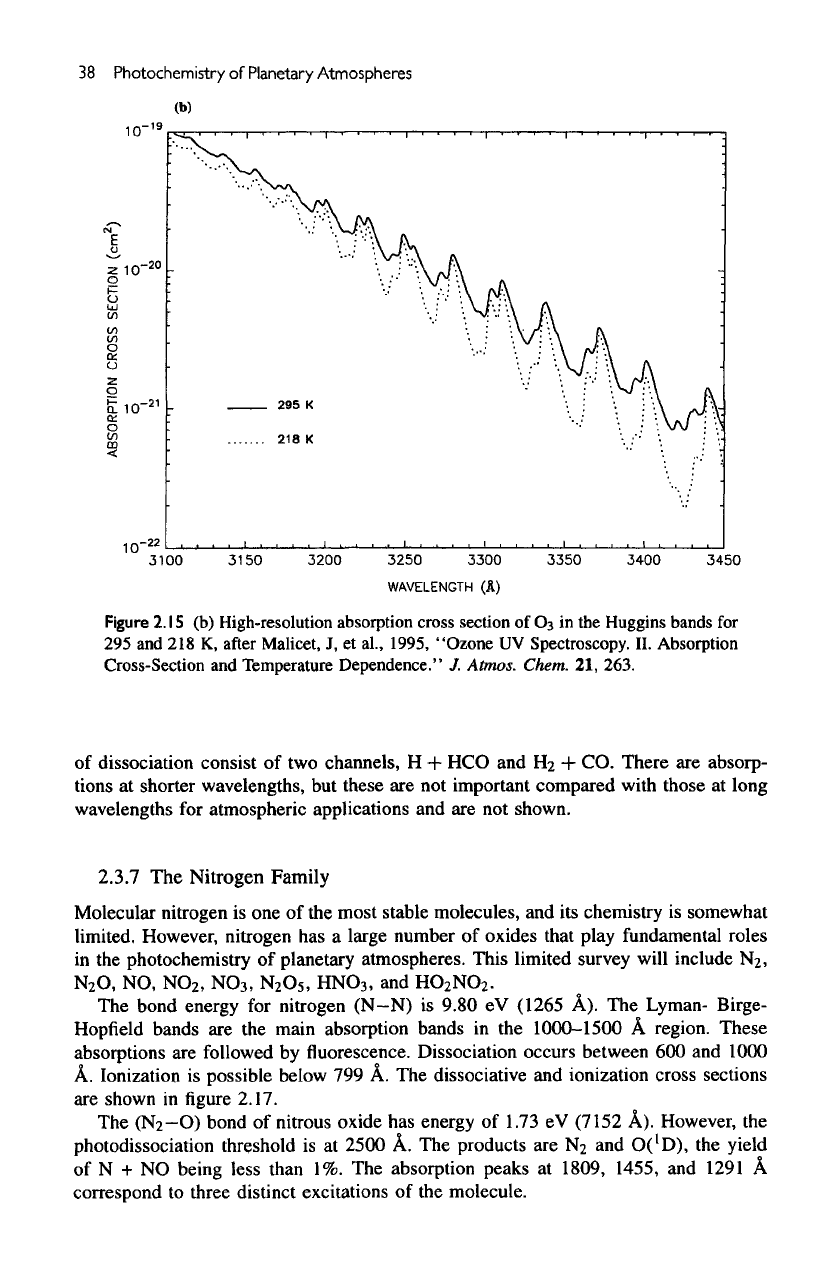
Figure
1.15
(b)
High-resolution absorption cross section
of
Os
in the
Huggins bands
for
295 and 218 K,
after
Malicet,
J, et
al.,
1995,
"Ozone
UV
Spectroscopy.
II.
Absorption
Cross-Section
and
Temperature
Dependence."
J.
Atmos.
Chem.
21,
263.
of
dissociation consist
of two
channels,
H + HCO and
H
2
+ CO.
There
are
absorp-
tions
at
shorter wavelengths,
but
these
are not
important compared with those
at
long
wavelengths
for
atmospheric applications
and are not
shown.
2.3.7
The
Nitrogen
Family
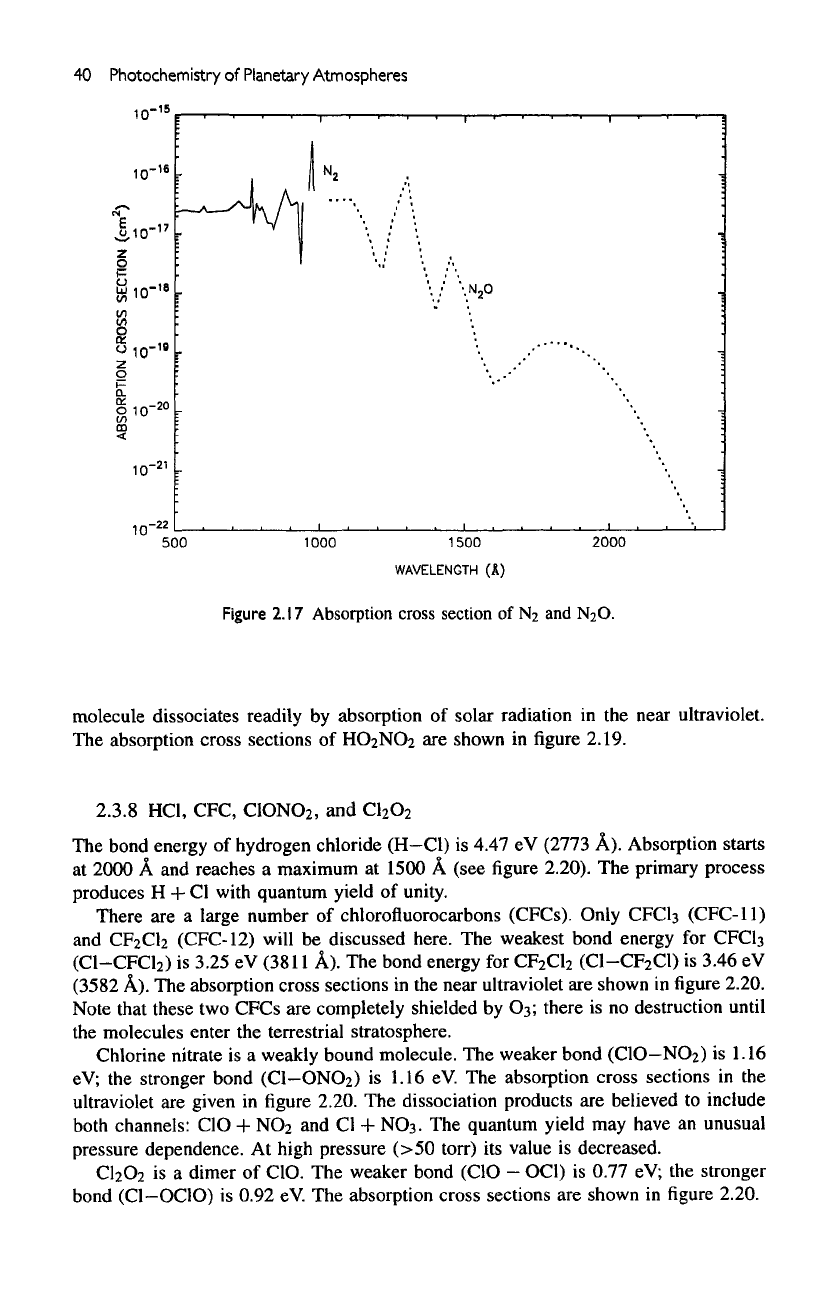
Molecular nitrogen
is one of the
most stable molecules,
and its
chemistry
is
somewhat
limited.
However, nitrogen
has a
large number
of
oxides that play fundamental roles
in
the
photochemistry
of
planetary atmospheres. This limited survey will include
N2,
N
2
O,
NO,
NO
2
,
NO
3
,
N
2
O
5
,
HNO
3
,
and
HO
2
NO
2
.
The
bond energy
for
nitrogen (N-N)
is
9.80
eV
(1265
A). The
Lyman- Birge-
Hopfield
bands
are the
main absorption bands
in the
1000-1500
A
region.
These
absorptions
are
followed
by
fluorescence. Dissociation occurs between
600 and
1000
A.
lonization
is
possible below
799 A. The
dissociative
and
ionization cross sections
are
shown
in figure
2.17.
The
(N
2
-O)
bond
of
nitrous oxide
has
energy
of
1.73
eV
(7152
A).
However,
the
photodissociation
threshold
is at
2500
A. The
products
are
N
2
and
O(
1
D),
the
yield
of
N + NO
being less than
1%. The
absorption peaks
at
1809, 1455,
and
1291
A
correspond
to
three distinct excitations
of the
molecule.

Solar Flux
and
Molecular
Absorption
39
Figure
2.16
Absorption
cross
section
of
CO2,
CO, and H2CO.
The
bond energy
of
nitric oxide (N-O)
is
6.55
eV
(1893
A).
Absorption begins
at
1910
A via the ft, y, S, and €
bands.
Predissociation
occurs with
the
absorption
of
radiation
below 1910
A.
This includes
the
states
v' > 6 for
/8
bands,
v'
> 3 for y
bands,
v'
> 3 for €
bands,
and all of S
bands. Figure
2.18
shows
the
absorption cross
sections
in the S
(0-0) bands.
The
bond energy
of
nitrogen
dioxide
(ON-O)
is
3.18
eV
(3903
A). At
long
wave-
lengths
beyond
the
dissociation limit,
NO
2
absorption
is
followed
by
fluorescence.
Figure
2.19
shows
the
absorption cross sections
of
NO
2
in the
ultraviolet.
The ab-
sorption
is
known
to be
slightly
dependent
on
temperature.
The
quantum yield
of
dissociation
is
unity
below
3130
A but
falls
off
rapidly
to
about
1%
at
4358
A.
Nitrogen
trioxide
has a
bond energy
(O-NO
2
)
equal
to
2.16
eV
(5731
A).
Fig-
ure
2.19
shows that there
is
strong absorption
in the
visible spectrum, between
4500
and
7000
A. The
principal products
are NO2 + O,
with only about
10%
contribution
of
the
product channel
NO +
O
2
.
Dinitrogen
pentoxide
has an
extremely weak bond
(O
2
N-NO
3
)
of
0.99
eV
(1.25
/zm).
The
molecule
is
barely stable against thermal decomposition
in the
terrestrial
atmosphere.
The
absorption cross sections
are
shown
in
figure
2.19.
There
is a
signif-
icant
temperature dependence.
The
weakest bond
in
nitric acid
(HO-NO
2
)
has
energy
of
2.15
eV
(5774
A).
The
primary process occurs
from
3100
to
2000
A
(see
figure
2.19),
with
quantum
yield
of
unity
for
products
OH +
NO
2
.
Below
1500
A
there
is
another well-defined
region
of
absorption.
The
bond
(HO
2
-NO
2
)
in
pernitric
acid
has
energy
1.0 eV. The
40
Photochemistry
of
Planetary
Atmospheres
Figure
2.17
Absorption
cross
section
of N2 and
N2O.
molecule
dissociates
readily
by
absorption
of
solar
radiation
in the
near ultraviolet.
The
absorption
cross
sections
of
HO
2
NO
2
are
shown
in figure
2.19.
2.3.8 HC1, CFC,
C1ONO
2
,
and
C1
2
O
2
The
bond energy
of
hydrogen chloride
(H-C1)
is
4.47
eV
(2773
A).
Absorption
starts
at
2000
A and
reaches
a
maximum
at
1500
A
(see
figure
2.20).
The
primary
process
produces
H +
Cl
with
quantum yield
of
unity.
There
are a
large number
of
chlorofluorocarbons
(CFCs).
Only
CFC1
3
(CFC-11)
and
CFaCh
(CFC-12)
will
be
discussed here.
The
weakest bond energy
for
CFCls
(C1-CFC1
2
)
is
3.25
eV
(3811
A). The
bond energy
for
CF
2
C1
2
(C1-CF
2
C1)
is
3.46
eV
(3582
A). The
absorption
cross
sections
in the
near ultraviolet
are
shown
in figure
2.20.
Note that these
two
CFCs
are
completely shielded
by 03;
there
is no
destruction
until
the
molecules enter
the
terrestrial stratosphere.
Chlorine
nitrate
is a
weakly bound molecule.
The
weaker bond
(CIO—NO
2
)
is
1.16
eV; the
stronger bond
(Cl—ONO
2
)
is
1.16
eV. The
absorption
cross
sections
in the
ultraviolet
are
given
in figure
2.20.
The
dissociation products
are
believed
to
include
both
channels:
CIO
+
NO
2
and Cl +
NOs.
The
quantum yield
may
have
an
unusual
pressure dependence.
At
high
pressure (>50
torr)
its
value
is
decreased.
C1
2
O
2
is a
dimer
of
CIO.
The
weaker bond
(CIO
-
OC1)
is
0.77
eV; the
stronger
bond
(C1-OC1O)
is
0.92
eV. The
absorption cross sections
are
shown
in figure
2.20.
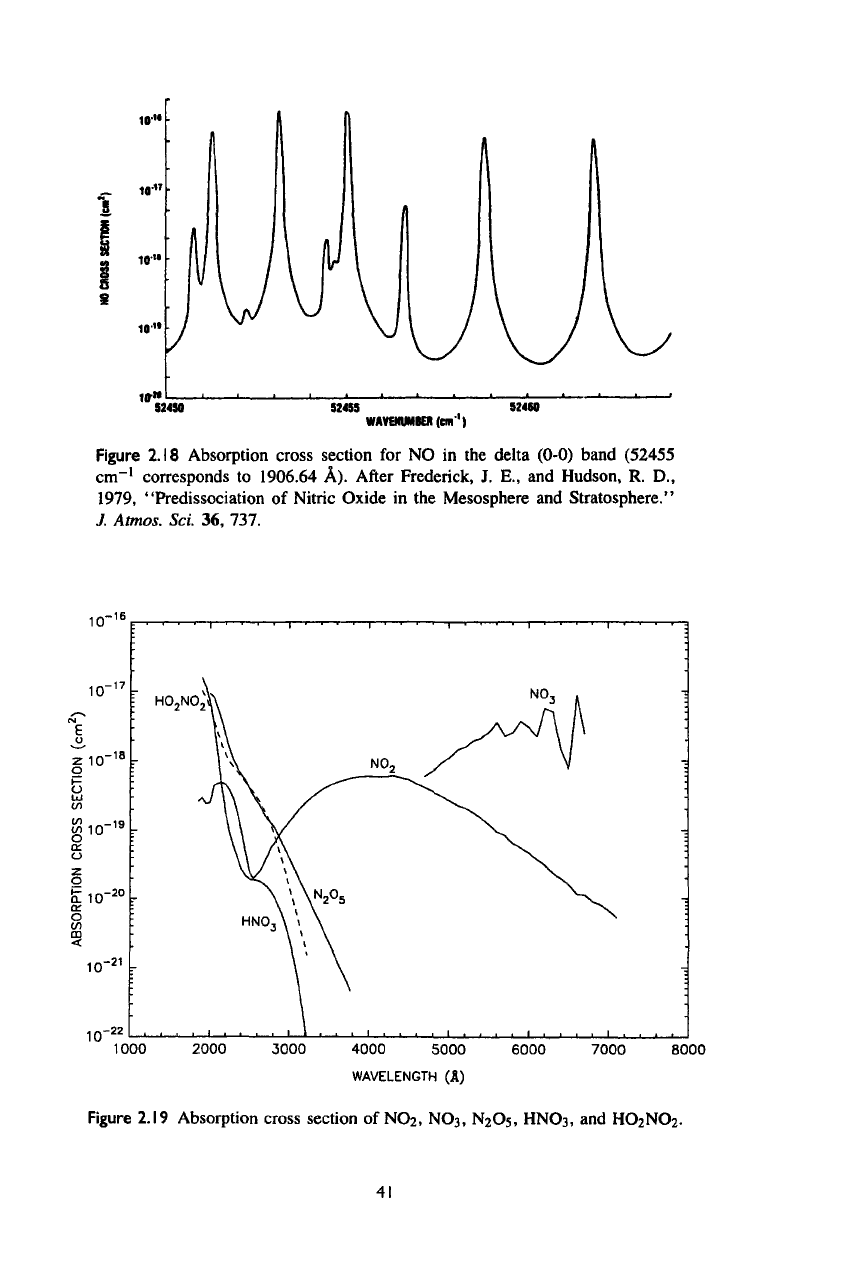
Figure
2.18
Absorption cross section
for NO in the
delta
(0-0)
band (52455
cm"
1
corresponds
to
1906.64
A).
After
Frederick,
J. E., and
Hudson,
R. D.,
1979,
"Predissociation
of
Nitric Oxide
in the
Mesosphere
and
Stratosphere."
J.
Amos.
Sci.
36,
737.
Figure
2.19
Absorption cross section
of
NO
2
,
NO
3
,
N
2
O
5
,
HNO
3
,
and
HO
2
NO
2
.
41
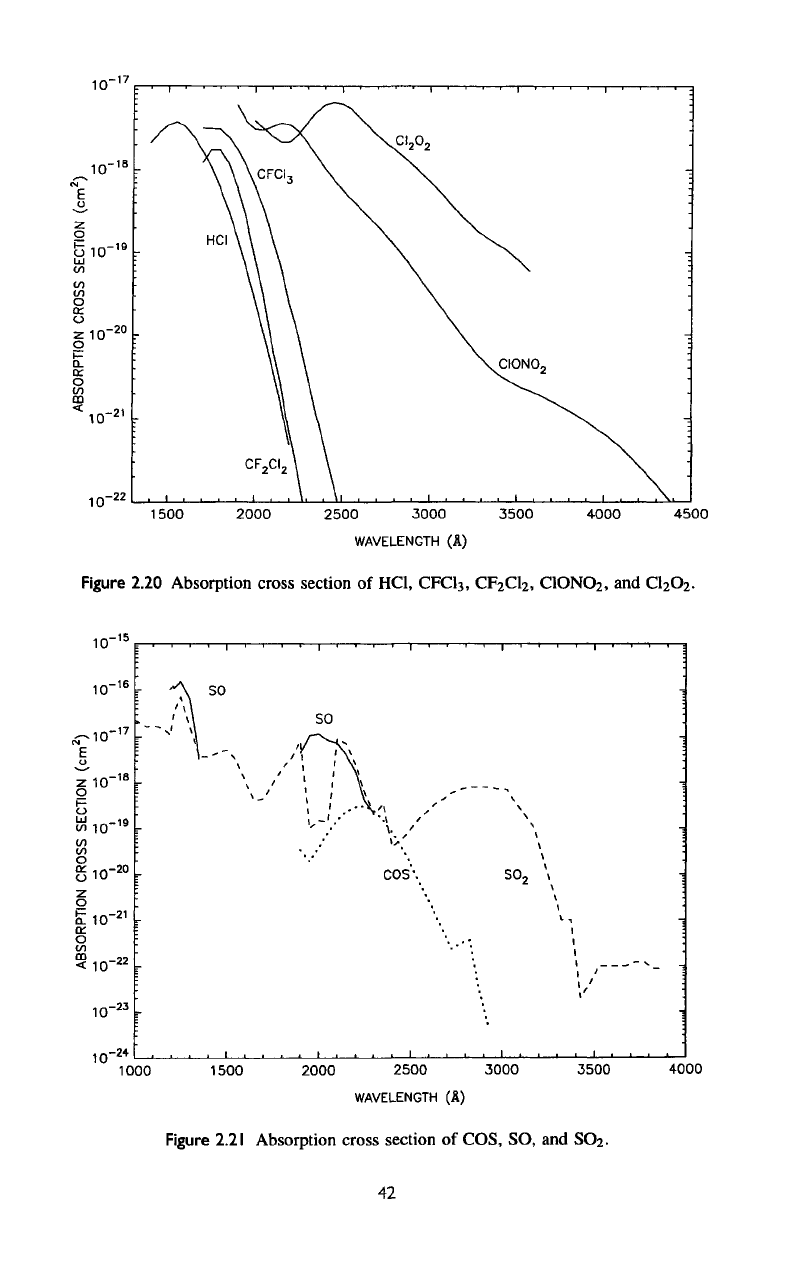
Figure
2.20
Absorption cross section
of
HCI,
CFC1
3
,
CF
2
C1
2>
C1ONO
2
,
and
C1
2
O
2
.
Figure
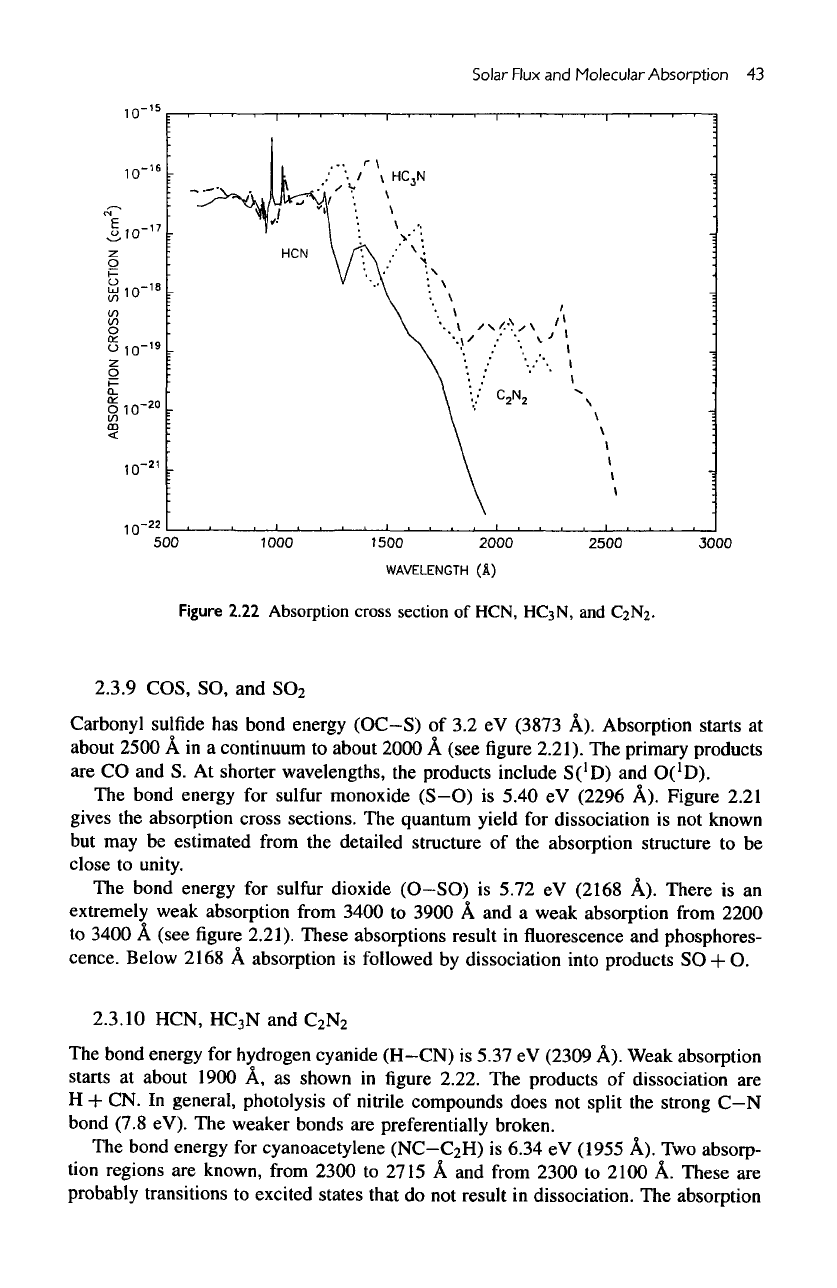
2.21
Absorption cross section
of
COS,
SO,
and
SO
2
.
42
Solar
Flux
and
Molecular
Absorption
43
Figure 2.22
Absorption
cross
section
of
HCN,
HC
3
N,
and
C
2
N
2
.
2.3.9 COS,
SO, and
SO
2
Carbonyl
sulfide
has
bond energy
(OC-S)
of 3.2 eV
(3873
A).
Absorption starts
at
about
2500
A in a
continuum
to
about
2000
A
(see
figure
2.21).
The
primary products
are CO and S. At
shorter wavelengths,
the
products include
S('D)
and
O('D).
The
bond energy
for
sulfur
monoxide
(S-O)
is
5.40
eV
(2296
A).
Figure 2.21
gives
the
absorption
cross
sections.
The
quantum yield
for
dissociation
is not
known
but
may be
estimated
from
the
detailed structure
of the
absorption structure
to be
close
to
unity.
The
bond energy
for
sulfur
dioxide
(O-SO)
is
5.72
eV
(2168
A).
There
is an
extremely
weak absorption from
3400
to
3900
A and a
weak absorption
from
2200
to
3400
A
(see
figure
2.21).
These
absorptions result
in fluorescence and
phosphores-
cence. Below 2168
A
absorption
is
followed
by
dissociation into products
SO + O.
2.3.10
HCN,
HC
3
N
and
C
2
N
2
The
bond energy
for
hydrogen cyanide
(H-CN)
is
5.37
eV
(2309
A).
Weak absorption
starts
at
about 1900
A, as
shown
in figure
2.22.
The
products
of
dissociation
are
H + CN. In
general, photolysis
of
nitrile
compounds
does
not
split
the
strong
C—N
bond (7.8 eV).
The
weaker bonds
are
preferentially broken.
The
bond energy
for
cyanoacetylene
(NC-C
2
H)
is
6.34
eV
(1955
A). Two
absorp-
tion
regions
are
known,
from
2300
to
2715
A and
from
2300
to
2100
A.
These
are
probably
transitions
to
excited states that
do not
result
in
dissociation.
The
absorption

44
Photochemistry
of
Planetary
Atmospheres
cross
sections below
2000
A are
shown
in figure
2.22.
The
photolysis products
are
most likely
CaH
+ CN. The
quantum yields
are
unknown.
The
bond energy
for
cyanogen
(NC-CN)
is
5.84
eV
(2123
A).
Weak absorption
bands
are
from
3020
to
2400
A and
from
2260
to
1820
A.
Strong absorption occurs
below
1800
A
(see
figure
2.22).
The
products
of
dissociation
are CN + CN.
2.4
Interaction
Between Solar
Radiation
and the
Atmosphere
2.4.1 Absorption
For a
plane parallel atmosphere containing
a gas
mixture
with
number densities
n,-(z),
we can
define
an
absorption optical depth
at
wavelength
A.
by
where
or/
(A.)
is the
absorption cross section
at
wavelength
A.
and z is the
altitude
(z
= 0
usually refers
to the
surface).
The
attenuation
of the
solar
flux
that enters
the
atmosphere
at
zenith angle
9 is
given
by the
expression
where
F(oo,
A.)
is the
solar
flux at the top of the
atmosphere
and
/i
=
cos0.
The
expo-
nential
factor
in
(2.7) suggests that
the
solar
flux is
rapidly attenuated
as it
penetrates
into
the
atmosphere when
the
absorption
is
strong
and the
optical depth
is
large.
The
volume absorption rate
by
species
i is
given
by
where
is
known
as the
photodissociation
coefficient.
The
units
of
F(z,
A.),
r/(z),
and
7,-
(2)
are
photons
cm~
2
s"
1
,
photons
cm"
3
s"
1
,
and
s"
1
,
respectively. Equation
(2.6)
ignores
the
curvature
of the
planet,
an
approximation that holds
in the
terrestrial atmosphere
until
9
exceeds
87°.
To
gain some
insight
into equations
(2.6)-(2.9),
we
examine
the
special
case
of
a
monochromatic beam
of
light incident
on an
isothermal atmosphere containing
a
single absorbing
species
whose concentration
is
given
by
where
H
is the
atmospheric scale height.
In
this
case
the
volume absorption rate
is
Solar Flux
and
Molecular
Absorption
45
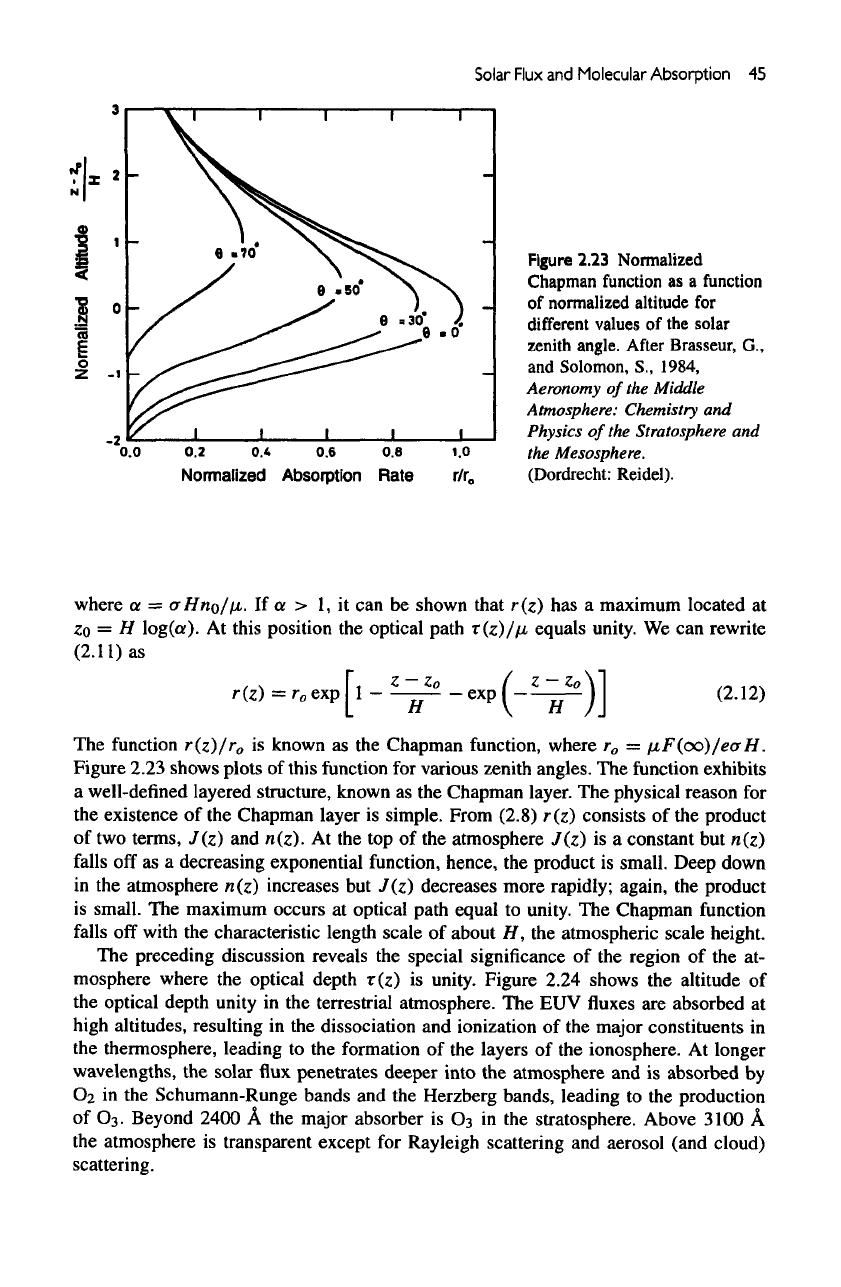
Figure
2.23
Normalized
Chapman
function
as a
function
of
normalized
altitude
for
different
values
of the
solar
zenith
angle.
After
Brasseur,
G.,
and
Solomon,
S.,
1984,
Aeronomy
of the
Middle
Atmosphere:
Chemistry
and
Physics
of the
Stratosphere
and
the
Mesosphere.
(Dordrecht:
Reidel).
where
a =
aHno/fji.
If a > 1, it can be
shown that r(z)
has a
maximum located
at
ZQ
=
H
log(a).
At
this position
the
optical path
r(z)//u
equals unity.
We can
rewrite
(2.
11)
as
The
function
r(z)/r
a
is
known
as the
Chapman
function,
where
r
0
=
fiF(oo)/eaH.
Figure
2.23 shows
plots
of
this function
for
various
zenith
angles.
The
function exhibits
a
well-defined layered structure, known
as the
Chapman layer.
The
physical reason
for
the
existence
of the
Chapman layer
is
simple. From (2.8)
r(z)
consists
of the
product
of
two
terms, J(z)
and
n(z).
At the top of the
atmosphere
J(z)
is a
constant
but
n(z)
falls
off as a
decreasing exponential function, hence,
the
product
is
small.
Deep
down
in
the
atmosphere n(z) increases
but
J(z)
decreases more rapidly; again,
the
product
is
small.
The
maximum occurs
at
optical path equal
to
unity.
The
Chapman
function
falls
off
with
the
characteristic length scale
of
about
H,
the
atmospheric scale height.
The
preceding discussion reveals
the
special significance
of the
region
of the at-
mosphere where
the
optical depth
r(z)
is
unity. Figure 2.24 shows
the
altitude
of
the
optical depth
unity
in the
terrestrial atmosphere.
The EUV
fluxes
are
absorbed
at
high
altitudes, resulting
in the
dissociation
and
ionization
of the
major constituents
in
the
thermosphere,
leading
to the
formation
of the
layers
of the
ionosphere.
At
longer
wavelengths,
the
solar
flux
penetrates
deeper
into
the
atmosphere
and is
absorbed
by
Oa
in the
Schumann-Runge
bands
and the
Herzberg bands, leading
to the
production
of
O
3
.
Beyond
2400
A the
major absorber
is 03 in the
stratosphere. Above 3100
A
the
atmosphere
is
transparent except
for
Rayleigh scattering
and
aerosol (and cloud)
scattering.
