Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

близости действительного и нормального потенциалов следует,

что разность U

—Ua будет близка к геопотенциальной величине

gdh:

Uo-U

* j* gdh. (19.3)

В формулах (19.2) и (19.3) U

и U

— значения нормального по-

тенциала в точке А и на эллипсоиде соответственно.

Заменим в формуле (19.3) приближенное равенство точным

£/

-£Ч = § gdh, (19.4)

где U

A±

— значение нормального потенциала в точке Ль располо-

женной на одной отвесной линии с точкой Л физической поверх-

ности Земли.

Из условия (19.3) следует, что точка А\ будет расположена

вблизи точки Л.

С учетом (19.4) равенство (19.2) для геодезической высоты

можно записать

-u

2Л1

+ ЛИ (19.6)

• m I т

где Ym°

2Al

, ym

AlA

— средние интегральные значения нормальной

силы тяжести на отрезках 0

А\ и А\

соответственно. Член

-U

y°J

• т

определяет высоту точки А\ над эллипсоидом, которую называют

нормальной высотой, член

Ua^UA

— С

* т

определяет отрезок Л1Л между точкой физической поверхности

Земли Л и точкой А\ и называется аномалией высоты.

Таким образом,

+ (19.6)

Итак, для определения геодезической высоты нужно найти нор-

мальную высоту

309;

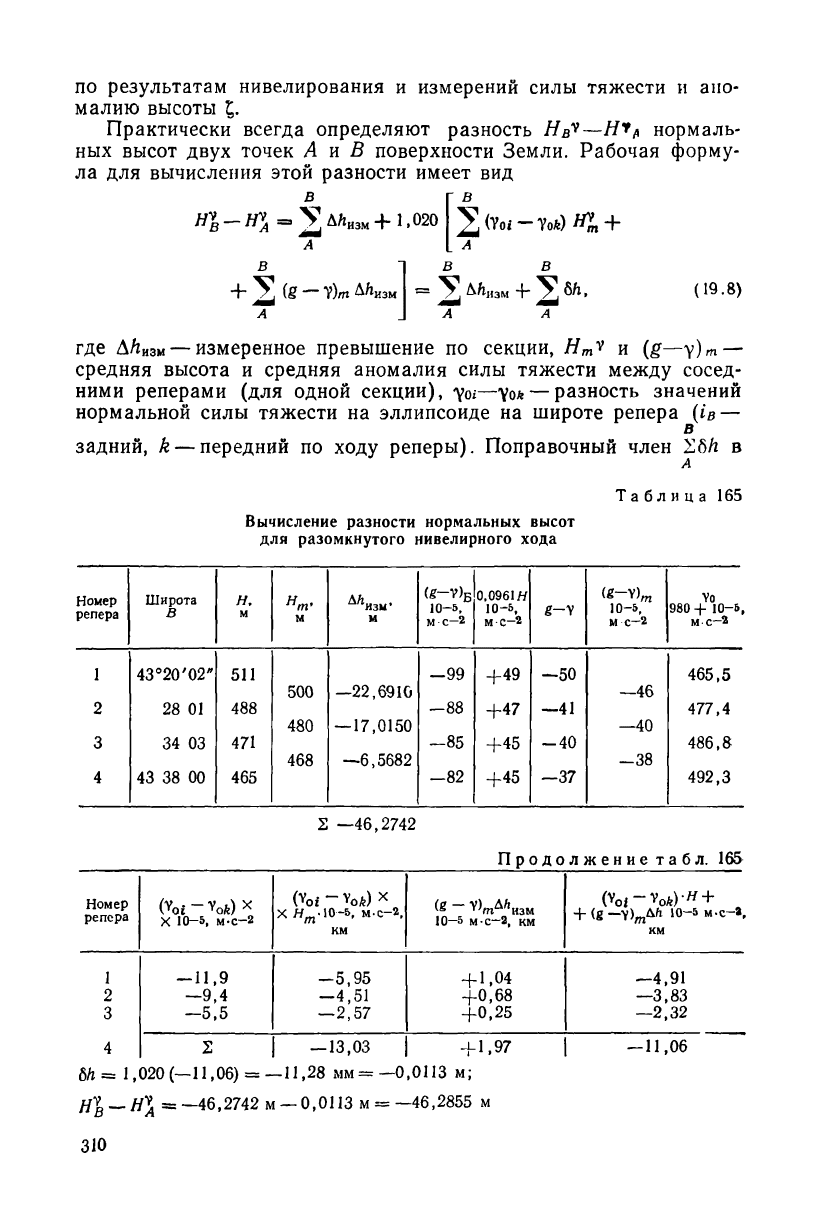
по результатам нивелирования и измерений силы тяжести и ано-

малию высоты

Практически всегда определяют разность Н

—нормаль-

ных высот двух точек А и В поверхности Земли. Рабочая форму-

ла для вычисления этой разности имеет вид

'А

А А

(19.8)

где ДЛизм —измеренное превышение по секции, H

f и (g—у)^ —

средняя высота и средняя аномалия силы тяжести между сосед-

ними реперами (для одной секции), yoi—Yo* — разность значений

нормальной силы тяжести на эллипсоиде на широте репера (ie —

задний, k — передний по ходу реперы). Поправочный член 26h в

Таблица 165

Вычисление разности нормальных высот

для разомкнутого нивелирного хода

Номер

репера

Широта

я,

(g-v)

ю-5,

С-2

0.0961Я

10-5,

С-2

g- У

(g-Y)

10-5,

С-2

980+ 10-5,

м-с-2

43°20

02"

511

-99

+49

-50

465,5

500 —22,6910

+49

—46

28 01

488

-88

+47

—41 477,4

480 — 17,0150

+47

—40

3 34 03

471

—85

+45

-40

486,8

468

—6,5682

+45

-38

4 43 38 00

465

-82

+45

—37

492,3

2 —46,2742

Продолжение табл. 165

Номер

репера

i-Y

ofe

X 10-5, м.С-2

(Vol —

OJfe

)

X H

-\0-b

м-с-2.

км

(g - Y)

H3M

10-5 м-С-2, КМ

(Yo|-Y

*)-tf +

+ (g-Y)

Aft Ю-5 м-с—

км

-11,9

—9,4

—5,5

-5,95

-4,51

—2,57

+ 1,04

+0,68

+0,25

—4,91

—3,83

—2,32

2 |

| —13,03

+ 1.97 |

| -11,06

bh = 1,020 (—11,06) = —11,28

мм —

—0,0113 м;

— = —46,2742

м —

0,0113

= —46,2855 м

измеренное превышение в формуле (19.8) выражен в миллимет-

рах при #m

и ДЛизм, выраженных в километрах, уо/—Уо*> (g—

—у)т — в Ю-

м-с~

. Коэффициент 1,020= ~~ перед квадратны-

V т

ми скобками получен для ^т=980-10-

м-с~

Как видно из формулы (19.8), для вычисления нормальных вы-

сот нужно знать аномалии силы тяжести в свободном воздухе,

для определения которых используют гравиметрические карты в

редукции Буге. Переход от аномалий Буге к аномалиям в сво-

бодном воздухе осуществляют по формуле

— 7 —

(£

—

7)б + 0,04186Я, (19.9)

где б — значение плотности промежуточного слоя, принятое при

построении гравиметрической карты; в СССР при построении гра-

виметрических карт обычно принимают

= 2,3 г/см

, тогда

—

V-

(G — ?)Б

-И.0961Я, (19.10)

где Н — высота в метрах.

Пример вычисления разности нормальных высот дан в табл.

165.

§ 95. Вычисление теоретической невязки

нивелирного полигона

Представим себе, что нивелирный ход проложен вдоль замкну-

того полигона. В этом случае разность потенциалов между конеч-

ными точками хода будет равна нулю

gdh — 0,

У"

а следовательно, будет равна нулю и разность нормальных вы-

сот. Напишем формулу (19.8) для замкнутого полигона

А А

К г

*иэм

0 » 2

ЛЛ

ИЗМ + 1.020 2 (Vol - Уок) Hm + ^(g- 7)т^и

A L А А

Отсюда можно найти м сумму измеренных превышений

в замкнутом полигоне, или теоретическую невязку нивелирного

полигона

/ = -1,020

(Vol

Уок)

+ 7)т^иэм

L А

(19.11)

311;

которая является следствием непараллельности уровенных по-

верхностей. Член (yot—Yofc) Нт учитывает непараллельность уро-

венных поверхностей нормального поля, член (g—y)hh

зм

— не-

совпадение уровенных поверхностей действительного и нормаль-

ного полей.

Таблица 166

Вычисление теоретической невязки нивелирного полигона

980ООО•

10"

м-с-»

Название пункта

Превыше-

ние, м

g>'

10-5

м-С-2

р.

10-5

м-С-2

- go,

10-5

м-С-2

f, мм

9804-

500 '

+750

287 287

—220

+750

074

—700 137

137

+98

200

+98

—80

452

+37

D 703

+830

529

—448

+830

355

—730 470

470 +350

585

+350

—70

542

+39

500

0 —144

Теоретическая невязка определяется одновременно с вычисле-

нием поправок 26h в измеренные превышения.

Приближенную оценку теоретической невязки протяженного

нивелирного полигона можно выполнить следующим образом. Для

разности потенциалов по замкнутому контуру напишем

ф gdh - ф (g - g

) dh + ф g

dh = 0,

где go — любое постоянное число.

Отсюда получаем

(19.12)

где g-

p — среднее значение силы тяжести для секции.

312

Глава 20

РЕДУЦИРОВАНИЕ НА ПОВЕРХНОСТЬ

РЕФЕРЕНЦ-ЭЛЛИПСОИДА

(НА ПОВЕРХНОСТЬ ОТНОСИМОСТИ)

ИЗМЕРЕННЫХ ГОРИЗОНТАЛЬНЫХ НАПРАВЛЕНИЙ,

БАЗИСОВ И НАКЛОННЫХ ДАЛЬНОСТЕЙ

Измеренные на поверхности Земли элементы геодезической се-

ти (длины сторон и горизонтальные направления) редуцируют к

поверхности принятого референц-эллипсоида. Теорию перехода

от измеренных на земле величин к соответствующим им величи-

нам на поверхности эллипсоида называют редукционной задачей

геодезии.

§ 96. Редукция горизонтальных направлений

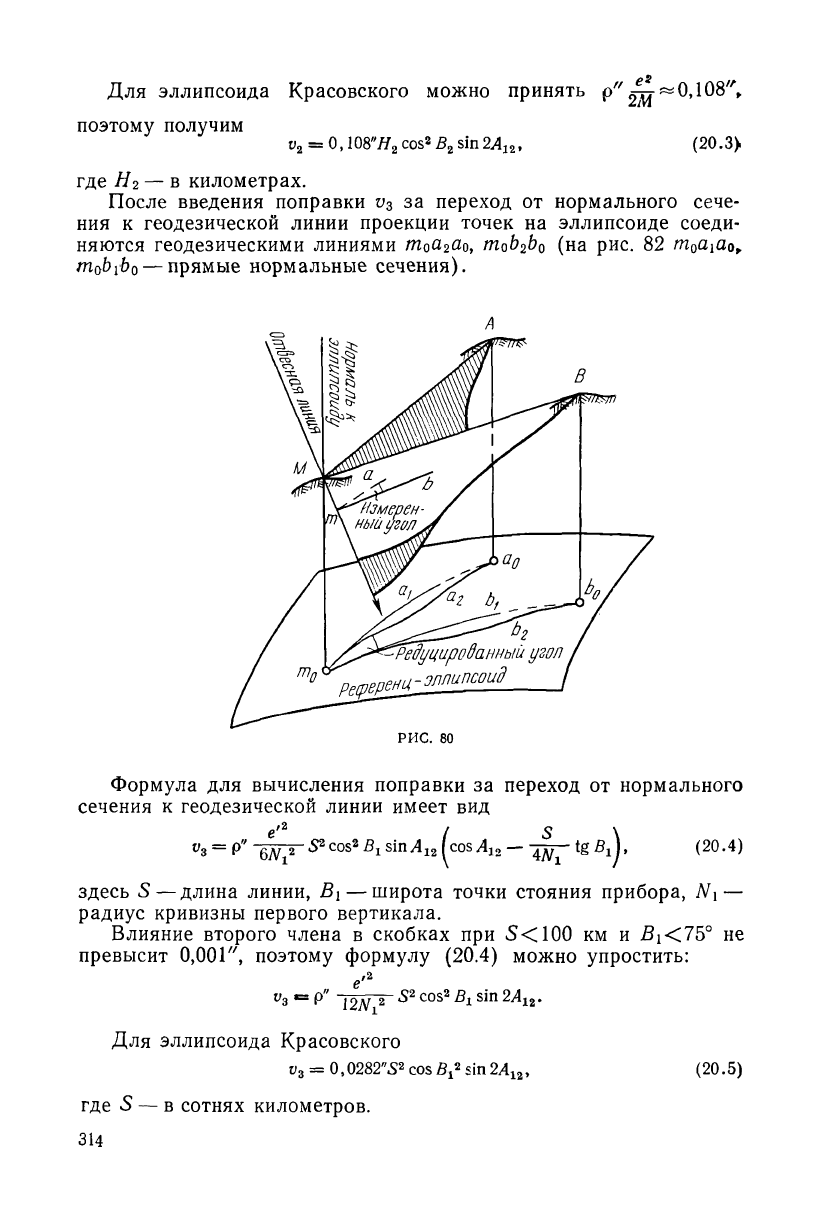
Для приведения к поверхности референц-эллипсоида в непос-

редственно измеренные горизонтальные направления вводят по-

правки за уклонение отвесной линии; за высоту наблюдаемого

предмета; за переход от нормального сечения к геодезической ли-

нии.

Введение поправки v

за уклонение отвесной линии означает

переход от непосредственно измеренного угла amb, являющегося

мерой двугранного угла, ребро которого совпадает с отвесной ли-

нией в точке М наблюдения, к двугранному углу, ребром которо-

го является нормаль Мт

к референц-эллипсоиду (рис. 80). Гра-

ни двугранных углов проходят через точки А и В физической по-

верхности Земли.

Поправку вычисляют по формуле

= (*li

cos Л

- £и

аг

Sin А

) cig г

, (20.1)

где £i

, T)i

—составляющие астрономо-геодезического уклонения

отвеса в точке стояния прибора, Л

— азимут, z

— зенитное рас-

стояние наблюдаемого направления.

Введение поправки v

за высоту наблюдаемого предмета пред-

полагает переход от граней, проходящих через точки Л и В, к гра-

ням, проходящим через их проекции на эллипсоид по нормалям

Аа

, ВЬо. Поправку находят по формуле

р"

-wrrе

cos

sin 2Л

, (20.2)

где Н

и В

— геодезическая высота и широта наблюдаемого пунк-

та соответственно, М— радиус кривизны меридиана, е — эксцент-

риситет.

313;

Для эллипсоида Красовского можно принять р" iL^O.lOe",

поэтому получим

= 0,108"Я

COS

sin 2Л

, (20.3>

где Н

— в километрах.

После введения поправки v

за переход от нормального сече-

ния к геодезической линии проекции точек на эллипсоиде соеди-

няются геодезическими линиями /П0Я2Я0, mob

(на рис. 82 /Ло^ао,

bib

— прямые нормальные сечения).

Формула для вычисления поправки за переход от нормального

сечения к геодезической линии имеет вид

= р"

52 cos2 sin А

12 (

cos А

12 - Щ- tg Si)

(20.4)

здесь S—длина линии, В\ — широта точки стояния прибора, N\ —

радиус кривизны первого вертикала.

Влияние второго члена в скобках при 5<100 км и £i<75° не

превысит 0,001", поэтому формулу (20.4) можно упростить:

е'

1>з «=

р" S

2 cos2 B

sin

2Л

Для эллипсоида Красовского

= 0,0282".S

cos

sin 2Л

, (20.5)

где 5 — в сотнях километров.

314

Выполним редуцирование треугольника (табл. 167—170)

триангуляции 1 класса на поверхность эллипсоида (рис. 81).

Сферический избыток треугольника вычисляют по формуле

(16.2).

§ 97. Редукция линейных измерений

Будем различать три вида линейных измерений:

измерение расстояний между точкой поверхности Земли и точ-

кой над Землей с помощью самолетного радиодальномера;

измерение расстояний между пунктами триангуляции свето-

или радиодальномером;

измерение базиса при помощи инварных проволок.

В первых двух случаях редуцирование измеренной линии S к

поверхности референц-эллипсоида проводят в два этапа: сначала

вычисляют хорду 5

соединяющую проекции точек 1 и 2 на по-

поверхность референц-эллипсоида (рис. 82), а затем переходят от

хорды Si к длине S

дуги на поверхности референц-эллипсоида.

Редуцирование линии, измеренной самолетным радиодально-

мером, выполняют по формулам

Г (S + AH)(S-m

I 9<V \

= + + (20.6,6)

В формулах (20.6) H

{

и Н

— геодезические высоты точки по-

верхности Земли и самолета, АН=Н

—Н

R — средний радиус

кривизны эллипсоида вдоль измеряемой линии, который можно вы-

числить по формуле

R = a(l + -у е* sin

— е

cos

\, (20.7)

315;

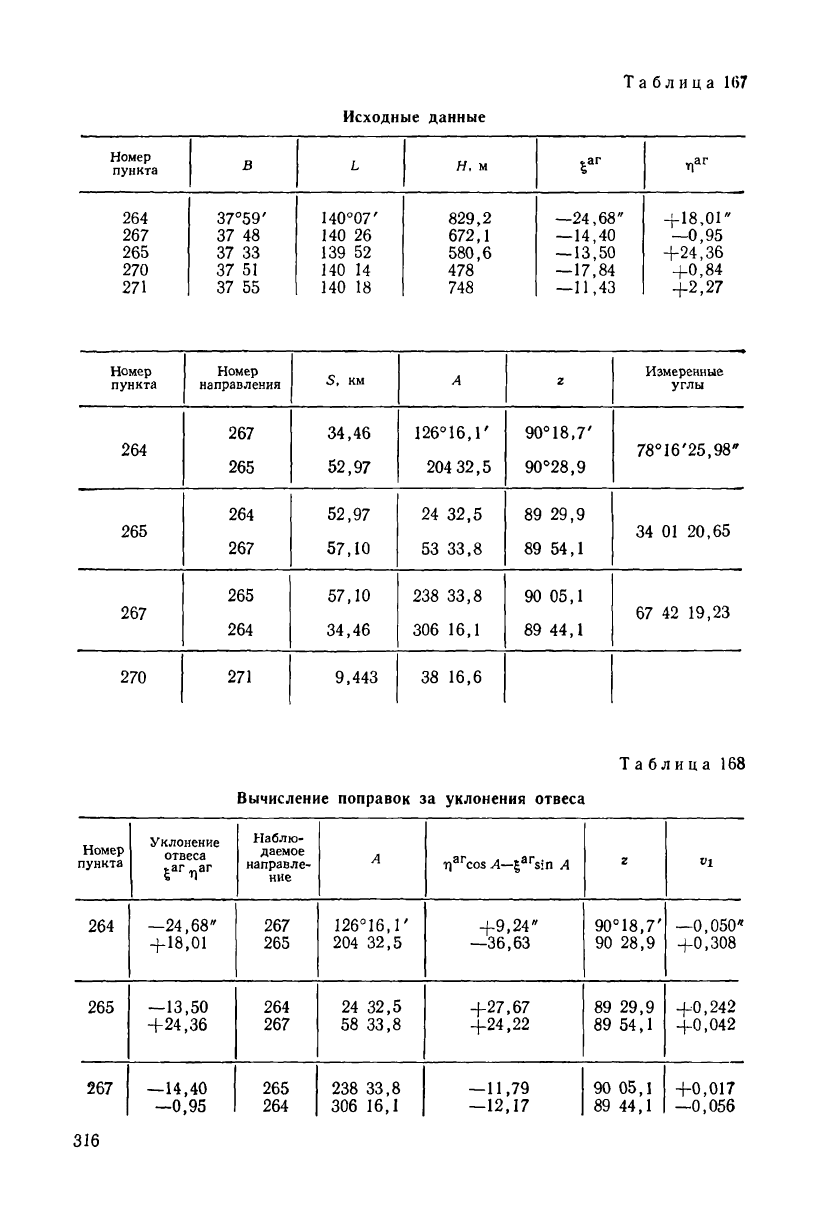
Таблица

187

Исходные данные

Номер

пункта

И, м

аг

264

37°59'

140°07'

829,2

—24,68"

18,01"

267

37 48 140 26

672,1

—14,40

—0,95

265

37 33 139 52

580,6

— 13,50

+24,36

270

37 51 140 14 478

—17,84

+0,84

271

37 55

140 18 748

—11,43 +2,27

Номер

пункта

Номер

направления

5, км А

Измеренные

углы

264

267

265

34,46

52,97

126°16,Г

204 32,5

90°18,7

90°28,9

78°16'25,98"

265

264

267

52,97

57,10

24 32,5

53 33,8

89 29,9

89 54,1

34 01

20,65

267

265

264

57,10

34,46

238 33,8

306 16,1

90 05,1

89 44,1

67 42 19,23

270 271

9,443

38 16,6

Таблица

168

Вычисление поправок

за

уклонения отвеса

Номер

пункта

Уклонение

отвеса

аг

аГ

Наблю-

даемое

направле-

ние

cos Л—£

sin

264

—24,68"

+18,01

267

265

126°16,1'

204 32,5

+9,24"

—36,63

90°18,7'

90 28,9

—0,050*

+0,308

265

—13,50

+24,36

264

267

24 32,5

58 33,8

+27,67

+24,22

89 29,9

89 54,1

+0,242

+0,042

267

—14,40

—0,95

265

264

238 33,8

306 16,1

—11,79

—12,17

90 05,1

89 44,1

+0,017

—0,056

316

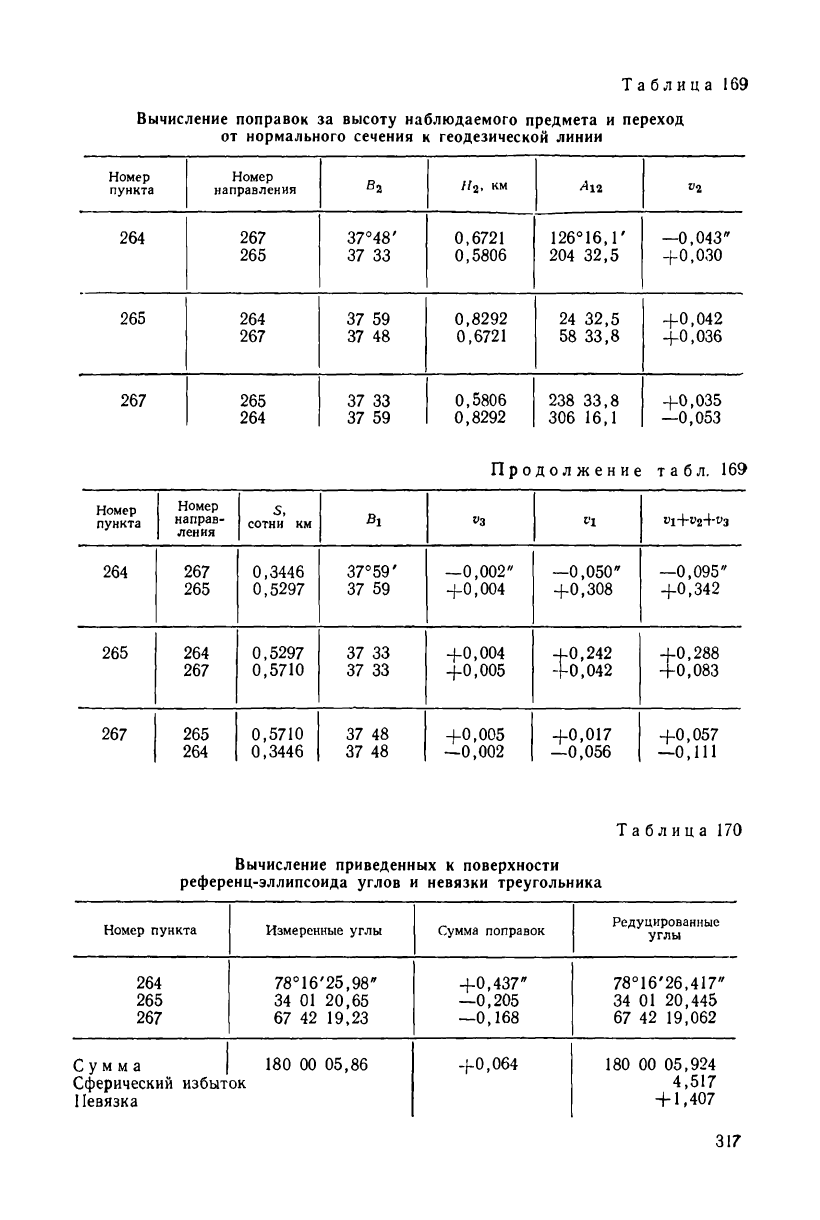
Таблица

187

Вычисление поправок за высоту наблюдаемого предмета и переход

от нормального сечения к геодезической линии

Номер

пункта

Номер

направления

Н2, км

А\2

264

267

265

37°48'

37 33

0,6721

0,5806

126°16,1'

204 32,5

—0,043"

+0,030

265

264

267

37 59

37 48

0,8292

0,6721

24 32,5

58 33,8

+0,042

+0,036

267

265

264

37 33

37 59

0,5806

0,8292

Про

238 33,8

306 16,1

должение

+0,035

—0,053

табл. 169

Номер

пункта

Номер

направ-

ления

сотни км

Vl-j-V

264

267

265

0,3446

0,5297

37°59'

37 59

—0,002"

+0,004

—0,050"

+0,308

—0,095"

+0,342

265

264

267

0,5297

0,5710

37 33

+0,004

+0,005

+0,242

+0,042

+0,288

+0,083

267

265

264

0,5710

0,3446

37 48

+0,005

—0,002

+0,017

—0,056

+0,057

—0,111

Таблица 170

Вычисление приведенных к поверхности

референц-эллипсоида углов и невязки треугольника

Номер пункта Измеренные углы Сумма поправок

Редуцированные

углы

264

265

267

78°16'25,98"

34 01 20,65

67 42 19,23

+0,437"

—0,205

—0,168

78°16'26,417"

34 01 20,445

67 42 19,062

Сумма |

Сферический избыток

Невязка

180 00 05,86

+0,064

180 00 05,924

4,517

+ 1,407

317

где е — эксцентриситет, В

— средняя широта линии, А\

— ее ази-

мут.

Формулы (20.6), (20.7) можно применять для редуцирования

расстояний порядка сотен километров.

При редуцировании непосредственно измеренных сторон триан-

гуляции, когда длина линии составляет десятки километров, фор-

мулы (20.6), (20.7) можно упростить и представить в виде

2 г

3Hf + ЗЯ

+ 2Н

(

24 R

- / Н.+Н» ЗЯ

+ ЗЯ

+ 2Н

НЛ

= V S

АЯ

^ 2R + 8R

")•

/? = а ^

1 —

-^-е* cos 2B

(20.8)

Для эллипсоида Красовского а = 6 378,245 км, е

= 0,006 693 422.

Если высоты Hi и Н

концов измеряемой линии не превышают

2 км, последний член в скобках можно не учитывать и вычислять

линию S

по формуле

= (i-

* ) + <

)

Пример 15. Редуцирование линейных измерений (табл.

171 —

172).

а) Редуцирование линии, измеренной самолетным радиодаль-

номером.

Исходные данные:

Измеренное расстояние 438 152 м

Геодезические координаты Si = 48°37

, Li = 74

31',

точки поверхности Земли #i = 143 м

Геодезические координаты В

= 45°03', L

= 71°57

самолета Н

= 3 764 м

Азимут измеренной линии Л

= 205°18

Порядок вычислений:

1. По формуле (20.7) вычисляют средний радиус референц-эл-

липсоида в азимуте линии R = 6373,3 км.

2. По формуле (20.6, а) вычисляют хорду 5! = 438 002,8 м.

3. Вычисляют поправку за переход от хорды S

{

к дуге S

/ 9 V \

—S

= 24У?

+ "80" "я

=я86

2 м<

4. Вычисляют редуцированное к поверхности референц-эллип-

соида расстояние

= S^

-J- («So —-

===

438

002,8

+ 86,2 м=:

438

089,0 м.

б) Редукция измеренного расстояния между пунктами триан-

гуляции.

Измерена линия между пунктами 264 и 267 (см. рис. 81).

318;