Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

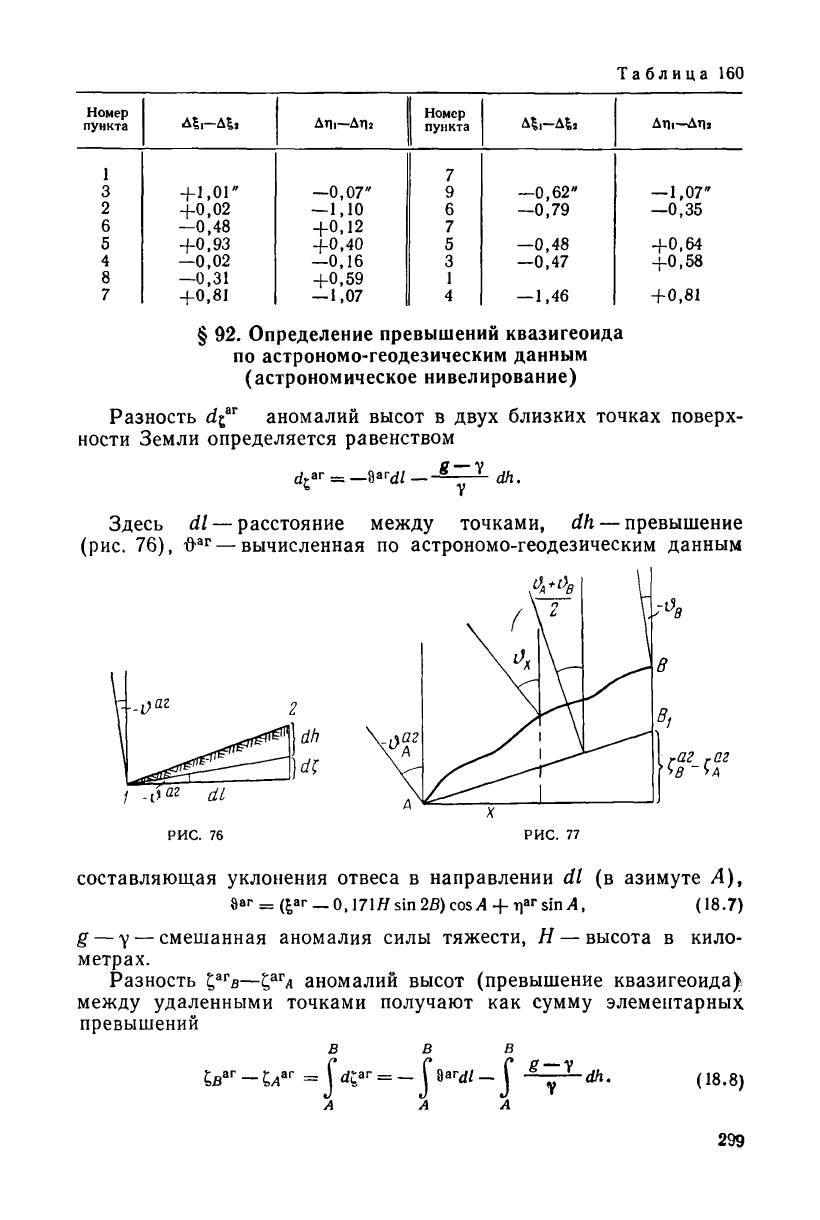
Таблица

187

Номер

пункта

AIi-Ala

АЛ i—АЛ 2

Номер

пункта

Атц—A*la

+1,01"

—0,07"

9 —0,62"

— 1,07"

+0,02

— 1,10

—0,79

-0,35

—0,48

+0,12

—0,79

-0,35

+0,93 +0,40

—0,48

+0,64

—0,02

—0,16

—0,47

+0,58

—0,31

+0,59

+0,58

+0,81

— 1,07

— 1,46

+0,81

§ 92. Определение превышений квазигеоида

по астрономо-геодезическим данным

(астрономическое нивелирование)

Разность d£

аномалий высот в двух близких точках поверх-

ности Земли определяется равенством

^аг

_ dh.

Здесь d/— расстояние между точками, dh— превышение

(рис. 76), вычисленная по астрономо-геодезическим данным

составляющая уклонения отвеса в направлении dl (в азимуте Л),

№

(£аг

— 0,171

tf sin

2В) cos А

+ т]

аг

sin А, (18.7)

g — у — смешанная аномалия силы тяжести, Н — высота в кило-

метрах.

Разность £

аг

в—£

аг

д аномалий высот (превышение квазигеоида)

между удаленными точками получают как сумму элементарных

превышений

в в в

£в

аг

-£л

аг

= J^

ar =

- J

1=1-

лл

(18 8)

A A A

299

Вычисление интегралов в правой части (18.8) возможно в том

случае, если вдоль линии АВ известны уклонения отвеса Ф

аг

и. ано-

малии силы тяжести g—В методе астрономического нивелирова-

ния предполагают, что уклонения отвеса между астропунктами А

1и В изменяются по линейному закону, т. е. в промежуточной точ-

ке на расстоянии х от начала линии оно равно

= V

+ I X. (18.9)

После подстановки (18.9) в формулу (18.8) и интегрирования

получают формулу астрономического нивелирования

£в

аГ

-£д

аГ

= - Т I, (18.10)

где I — расстояние между астропунктами.

Второй член правой части (18.8) в равенстве (18.10) не учи-

тывают. Применение формулы (18.10) предполагает, что поверх-

ность квазигеоида между астропунктами Л и В заменена плос-

костью, наклон которой равен среднему уклонению отвеса между

астропунктами (рис. 77). Точность астрономического нивелирова-

ния зависит главным образом от того, насколько действительные

уклонения отвеса Ф

аг

отличаются от интерполированных по форму-

ле (18.9). Средняя квадратическая погрешность астрономического

нивелирования по линии длиной L равна

/и

= ^ 10» VI, км L, км; Щ = °>

17"

уГГЯ*. (18.11)

Точность астрономического нивелирования существенно зави-

сит от расстояния между астропунктами.

Рабочую формулу астрономического нивелирования получают

после подстановки равенства (18.7) в (18.10) и использования за-

висимостей

lcosA = RAB; IsinA — R cos В

М, (18.12)

R— средний радиус Земли, В

— средняя широта линии, АВ и

AL — разности широт и долгот астропунктов соответственно.

Рабочая формула имеет вид

£в

аг

-£л

аг

= -[&А*

+ £в

аг

-0,171 (Я

+ Н

) Sin 2 В) А В + (Т1

аг

^ar)

S В

Щ , (18.13)

где 2р"р' =0>00449; АВ и AL — в минутах; ц — в секундах дуги.

Выполним астрономическое нивелирование по линии 1—4—8—

—7—9—6—2—3—1 (см. рис. 74). Так как точность астрономо-

геодезических уклонений отвеса составляет около 0,05", член

0Д71Х

(НА

+ НВ) sin 2В в равнинном районе можно не учитывать.

Пример вычисления дан в табл. 161.

300;

Таблица

161

Определение превышений квазигеоида методом астрономического нивелирования

Номер

пункта

В L

аг

АВ

Л L

+ b

ти

аг

Ч2

аг

/, км

60°59' 22°36'

— 1,23"

—3,39"

+44'

+20'

61°2Г

-0,51"

—4,08"

+0,276

83,5

61 43

22 56

+0,72

—0,69

+59

—3

62 12

+2,29

—0,91

—0,612

109,4

62 42

22 53

+ 1,57

—0,22

—09

+ 113

62 38

+0,98

-2,11

+0,532

97,7

62 33

24 46

—0,59

-1,89

+ 10 +62 62 38

+0,98

—0,87

+0,067

56,0

62 43

25 48

+ 1,57

+ 1,02

—52 -42

62 17

-0,52

—0,46 —0,162

102,9

61 51

25 06

—2,09

— 1,48

—50

-38 61 26

-3,86

+0,61

—0,817

98,6

61 01

24 28

— 1,77

+2,09

+07

-40

61 04

-1,82

+2,02

+0,233

38,2

3 61 08 23 48

—0,05

-0,07

—09

-72 61 04

—1,28

—3,46

—0,593

66,7

60 59

22 36

—

1,23

—3,39

I °

-1,076

653,0

ср

—тг—

= 81,6 км

Оценку точности выполним по формулам (18.11)

] 54"

о,

17"

у/81,6

= 1,54"; m

= -Ь— Ю

/81,6-653,0 = 1,72 м. (18.14)

§ 93. Определение превышений квазигеоида

методом астрономо-гравиметрического нивелирования

В методе астрономо-гравиметрического нивелирования астроно-

мо-геодезические уклонения отвеса Ф

аг

вдоль линии нивелирова-

ния вычисляют по формулам (18.4) § 91. В этом случае формула

(18.8) принимает вид

£в

гр

-£л

гр

+ Т М- (

£в

аг

£л

аг

—

1 +

dh.

Член в квадратных скобках называют гравиметрической по-

правкой в астрономическое нивелирование. Этот член учитывает

нелинейность изменения уклонений отвеса между астропунктами

и зависимость аномалий высоты £ от высоты над эллипсоидом.

Равенство (18.15) получено при условии, что гравиметрические

аномалии £

гр

высоты и уклонения отвеса связаны таким же со-

отношением, что и астрономо-геодезические (равенство (18.8):

в в

Ев

гр

- U

= - j *

dl - j

A A

Это соотношение выполняется только в том случае, если £

гр

Р вычислены с учетом аномалии силы тяжести по всей Земле

или в одной и той же области для обоих астропунктов А и В.

Практически удобнее вычислять £

гр

и v

с учетом аномалий силы

тяжести в скользящей круговой области с центром в каждом аст-

ропункте, при этом аномалии высот вычисляют по видоизмененной

формуле Стокса

2Я

ГРв

4^TJ J (ff-Y) [$(!>)-m)] Sin ypthpda, (18.16)

о о

где — значение функции Стокса на границе круговой обла-

сти радиуса

Рабочая формула астрономо-гравиметрического нивелирования

имеет вид

£в

аг

- L*

- £в

гр

- Ел

гр

- 0,00449 т

+ Л^)ЛВ +

+ (Дтм + Дт

]в

) cos В

М\, (18.17)'

где = |

аг

— £

Р — 0,171Н sin 2В, Лг] = т)«

— Г)

Р.

Поправку за кривизну нормальной силовой линии, равную

0,171 Я sin 2В, в равнинных районах можно не учитывать.

Вычисление гравиметрических уклонений отвеса и аномалий

высот по формулам (18.2) и (18.16) выполняют методом числен-

302;

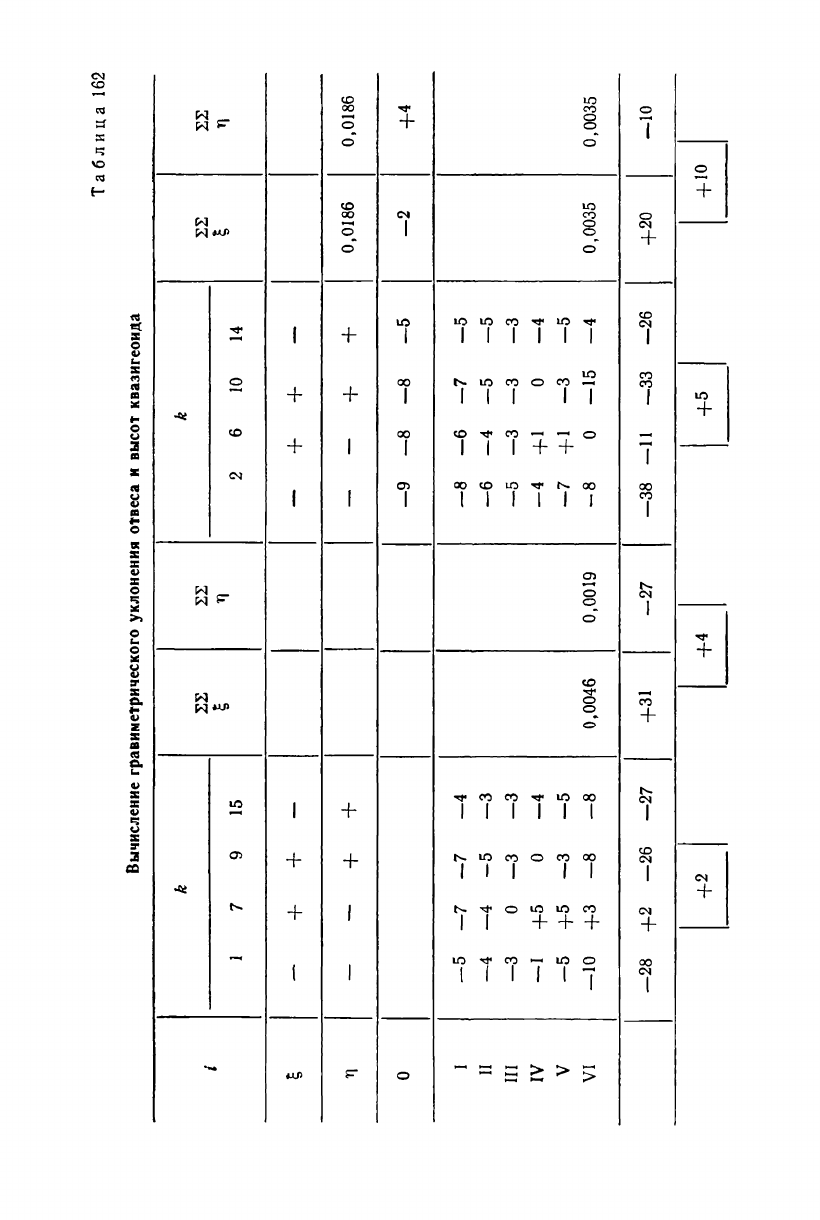
Таблица 162

Вычисление гравиметрического уклонения отвеса и высот квазигеоида

17 9 15

2 6 10 14

+ + -

- + + -

- - + +

0,0186 0,0186

—9 —8 —8 —5

—2

III

—5 -7 -7 -4

—4 —4 -5 —3

—3 0 —3 —3

— I +5 0 —4

—5 +5 —3 —5

—10 +3 -8 —8

0,0046

0,0019

—8 —6 —7 —5

—6 -4 —5 —5

—5 —3 —3 —3

—4 +1 0 —4

—7 +1 -3 —5

—

8 0 -15 -4

0,0035

—28 +2 —26 —27

+31

-27

—38 —11 —33 -26

+20

—10

+2 +4 +5 +10

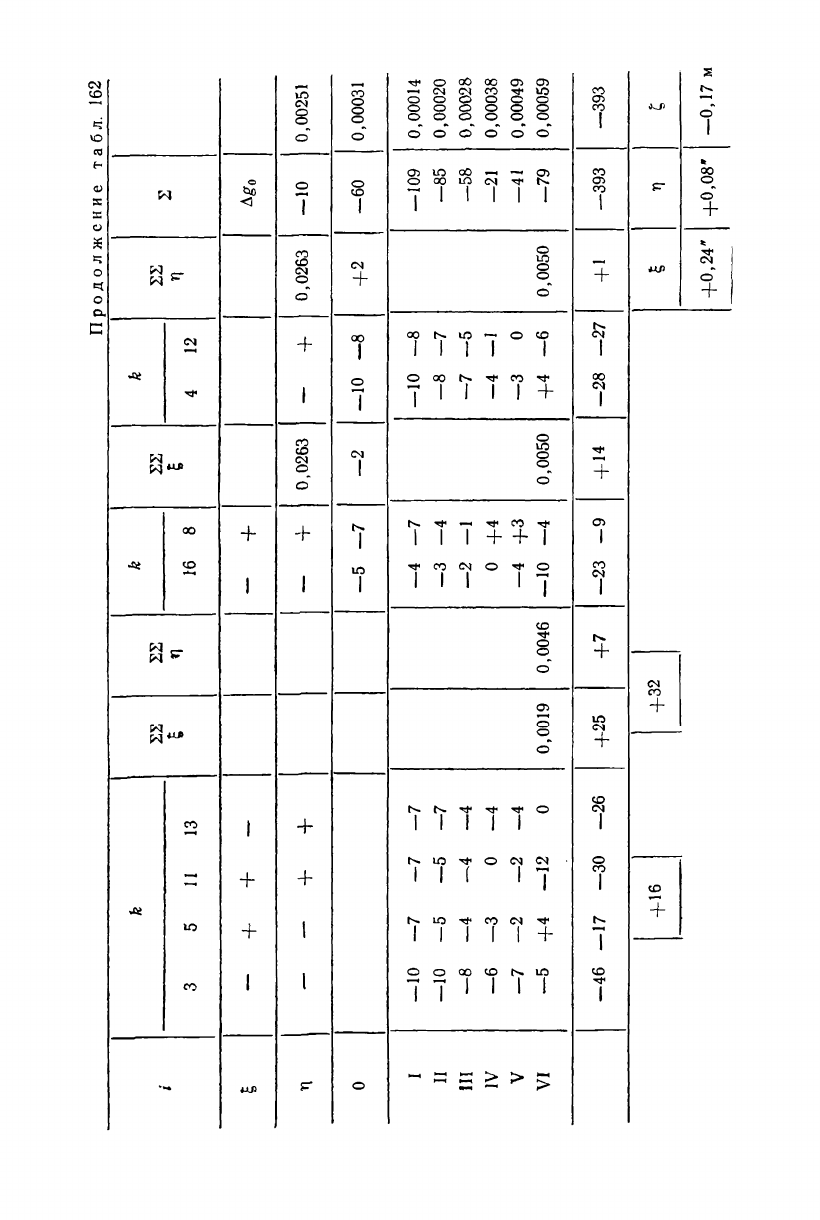
Продолжение табл. 151

2 i

3 5 11 13

16 8

4 12

- + + -

- +

- - + +

— +

0,0263

- +

0,0263

—10

0,00251

—5 —7

—2

-10 -8

-60

0,00031

III

—10 —7 —7 —7

—10 -5 —5 —7

—8 —4 —4 —4

—6 —3 0 —4

—7 —2 —2 —4

—5 +4 —12 0

0,0019

0,0046

—4 —7

-3 —4

—2 —1

0 +4

—4 +3

— 10 —4

0,0050

— 10 —8

—8 —7

—7 -5

-4 -I

—3 0

+4 —6

0,0050

— 109

-85

-58

—21

—41

-79

0,00014

0,00020

0,00028

0,00038

0,00049

0,00059

—46 —17 —30 —26

+25

—23 -9

+ 14

-28 —27

—393

+16 +32

"П

+0,24"

+0,08"

—0,17 м

ного интегрирования. Область в радиусе 48,5 км от астропункта

учитывают по гравиметрической карте, применяя палетку Еремее-

ва. Влияние аномалий силы тяжести в области радиусом 48,5км

^Rty^Rtyo вычисляют на ЭВМ с использованием средних анома-

лий силы тяжести в трапециях 10'Х15'.

Рассмотрим технику вычисления с применением палетки Ере-

меева. Так как в этом случае учитывается область до 48,5 км,

можно использовать формулы

для плоской отсчетной поверхно-

сти. Тогда вместо формул (18.2)

и (18.16) можно написать

2л Го

Р" Г Г ё — у

C0Si

£ГР

rfP

Р" С С G-

2яу J J г

О о

sin

2Л г Q

drdA,

(18.18)

(18.19)

где г

= 48,5 км — радиус облас-

ти интегрирования, г — расстоя-

ние до текущей точки от астро-

пункта, А — азимут.

Область интегрирования в

пределах от 5 до 48,5 км разби-

вают на шесть кольцевых зон равного влияния; каждая зона раз-

деляется на 16 секторов (рис. 78). Аномалия силы тяжести в пре-

делах каждой ячейки заменяется ее средним значением (g—y)i

(i — номер зоны, k — номер сектора). Тогда формулы (18.18) и

(18.19) примут вид

tro t

VI 16

гр

Со

+ 0,0000637 2 (

~ "77 )

Лг

2 ~

y)ik

i= I

k=\

где Ло, Co— влияние центральной зоны радиуса 5 км, А

= g- х

ХЛ —средний азимут сектора, г

р — средний радиус зоны, Дг —

ширина зоны в километрах.

Центральную зону в равнинных районах при спокойном поле

аномалий можно учитывать по формулам

;

= -0,0263" 2 (ё-У)п

cos А

sin

Со

= 0,00251 (g-y)

0,00031

2 (g

20—2296

305

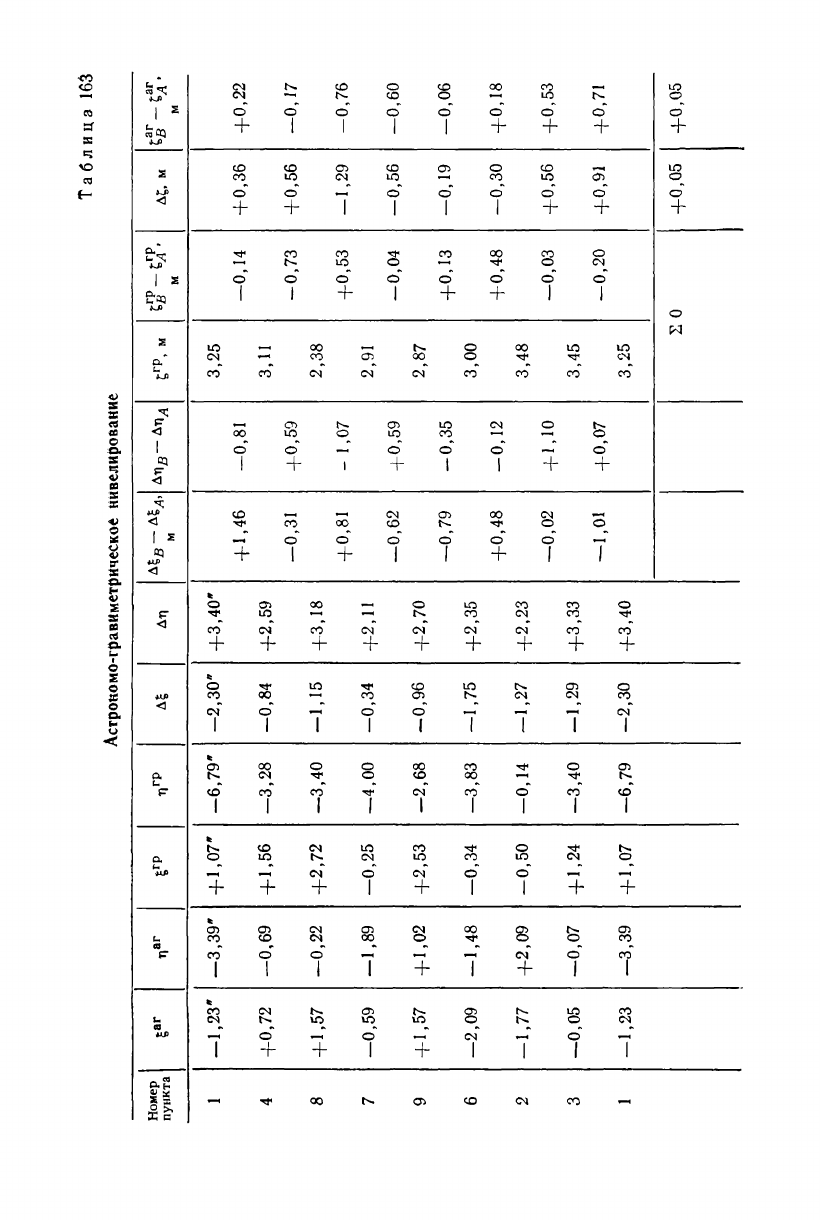
Таблица

163

Астрокомо-гравиметрическое нивелирование

Номер

пункта

аг

гр

А£

Д-р

ГР

> М

гр

В М '

Д£, м

«.аг

аг

*»в —

—1,23"

+0,72

+1,57

—0,59

+1,57

—2,09

— 1,77

—0,05

—1,23

—3,39"

—0,69

—0,22

— 1,89

+ 1,02

-1,48

+2,09

—0,07

—3,39

+ 1,07"

+1,56

+2,72

—0,25

+2,53

—0,34

-0,50

+ 1,24

+ 1,07

-6,79"

—3,28

—3,40

—4,00

—2,68

—3,83

—0,14

—3,40

—6,79

—2,30"

—0,84

— 1,15

—0,34

—0,96

-1,75

— 1,27

— 1,29

—2,30

+3,40"

+2,59

+3,18

+2,11

+2,70

+2,35

+2,23

+3,33

+3,40

+ 1,46

-0,31

+0,81

-0,62

—0,79

+0,48

—0,02

— 1,01

-0,81

+0,59

- 1,07

+0,59

-0,35

-0,12

+ 1,10

+0,07

3,25

3,11

2,38

2,91

2,87

3,00

3,48

3,45

3,25

—0,14

-0,73

+0,53

-0,04

+0,13

+ 0,48

—0,03

-0,20

+0,36

+0,56

— 1,29

—0,56

—0,19

—0,30

+0,56

+0,91

+0,22

-0,17

-0,76

—0,60

—0,06

+0,18

+0,53

+0,71

2 0

+0,05 +0,05

(g—Y) —значение аномалии силы тяжести в астропункте (в цент-

ре области интегрирования), (g—— значения аномалий силы

тяжести на окружности радиуса 5 км, A

=^ п

/г=1, 2, 8.

Пример вычисления гравиметрических уклонений отвеса и ано-

малий высот дан в табл. 162. Результат вычисления превышений

квазигеоида по формуле (18.17) приведен в табл. 163, 164.

Оценка точности астрономо-гравиметрического нивелирования

выполняется по формулам

1/ ШВ-ЧА)

]

У 2п

_у .1(АТ)В-Аты)«1

Ша Т1

2п

= 0,57";

= 0,49";

-У-

•т

АП

= 0,53".

да

—

у 2

Ошибка на 1 км хода

\i = т^ УТ7

« 4,79" УU км;

= г- "КГГкм^ 10

= 0,593 м.

(18.20)

Сравнение формул (18.20) и (18.14) подтверждает более вы-

сокую точность астрономо-гравиметрического нивелирования по

сравнению с астрономическим.

Таблица 164

Астрономо-гравиметрическое нивелирование

Номер

пункта

А В

A L

тп

Алл

+ Дт1

At. м

км

60°59'

22°36'

+44'

+20'

61°21'

—3,14"

+5,99"

+0,362

83,5

4 61 43

22 56

+44'

+20'

+59

—3 62 12

— 1,99 +5,77

+0,563 109,4

8 62 42

22 53

+59

—9

+ 113

62 38

— 1,49

+5,29

-1,294

97,7

7 62 33

24 46

+ 113

+ 10

+62

62 38

— 1,30

+4,81

—0,557

56,0

62 43

25 48

+ 10

+62

—52

-42

62 17

—2,71

+5,05

—0,190 102,9

61 51

25 06

+5,05

—50

-38

61 26

—3,02 +4,58

—0,304

98,6

61 01

24 28

+4,58

—40

61 04

-2,56

+ 5,56

+0,564

38,2

61 08

23 48

+0,564

—9

—72

61 04

-3,59

+6,73

+0,908 66,7

20*

j+0,052

653,0

307

Глава 19

ВЫЧИСЛЕНИЕ НОРМАЛЬНЫХ ВЫСОТ

§ 94. Вычисление разности нормальных высот

В соответствии с общим принципом определения высот в гра-

витационном поле высота равна отношению разности потенциа-

лов к среднему интегральному значению силы тяжести между со-

ответствующими уровенными поверхностями. Для геодезической

высоты Н можно написать

Я =

Wo, - wА

ёт

(19.1)

где Wo

—Wa — разность потенциалов между точкой Л физической

поверхности Земли и точкой 0

отсчетного эллипсоида, g

— сред-

нее интегральное значение силы

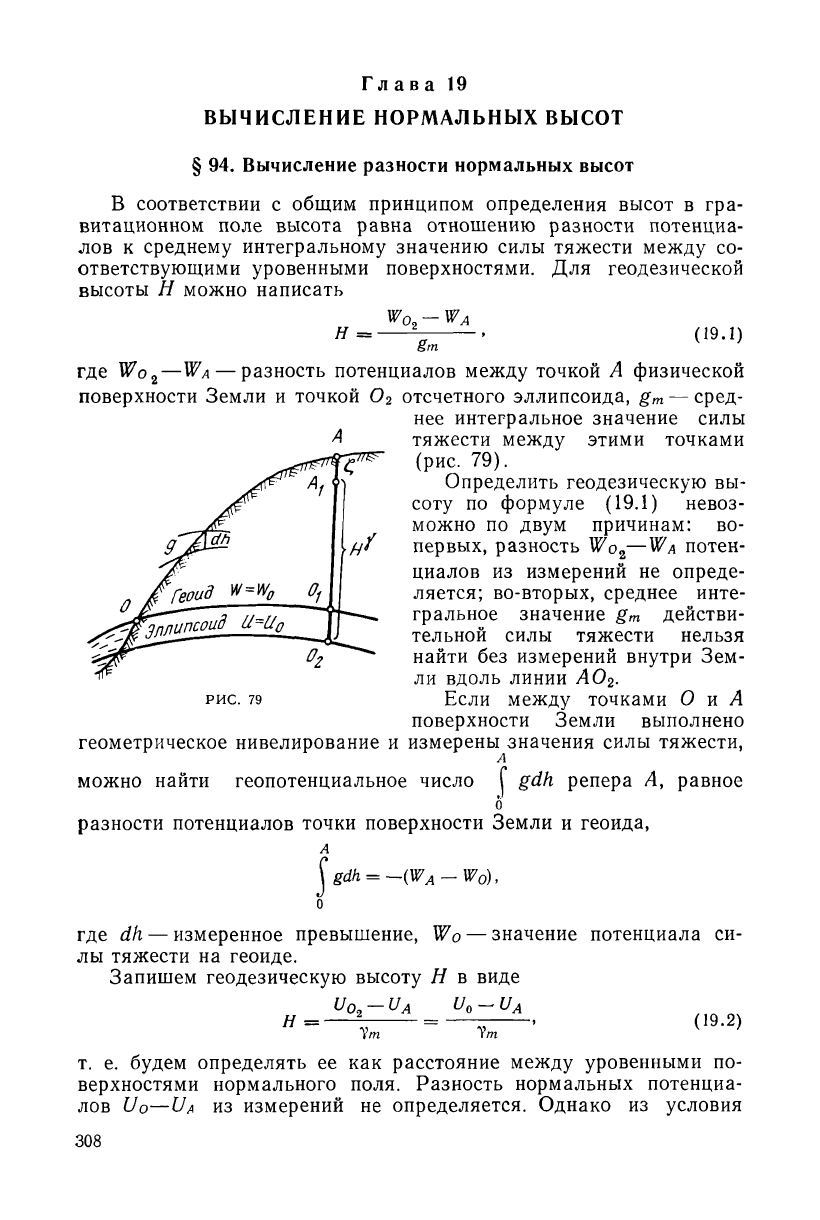
А тяжести между этими точками

(рис. 79).

Определить геодезическую вы-

соту по формуле (19.1) невоз-

можно по двум причинам: во-

первых, разность Wo

—Wa потен-

циалов из измерений не опреде-

ляется; во-вторых, среднее инте-

гральное значение g

действи-

тельной силы тяжести нельзя

найти без измерений внутри Зем-

ли вдоль линии Л0

Если между точками О и Л

поверхности Земли выполнено

геометрическое нивелирование и измерены значения силы тяжести,

можно найти геопотенциальное число j* gdh репера Л, равное

разности потенциалов точки поверхности Земли и геоида,

gdh = -(W

-W

РИС. 79

где dh — измеренное превышение, Wo — значение потенциала си-

лы тяжести на геоиде.

Запишем геодезическую высоту Н в виде

я =-

-UA Vo-U

Ут

(19.2)

т. е. будем определять ее как расстояние между уровенными по-

верхностями нормального поля. Разность нормальных потенциа-

лов Uo—Ua ИЗ измерений не определяется. Однако из условия

308;