Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

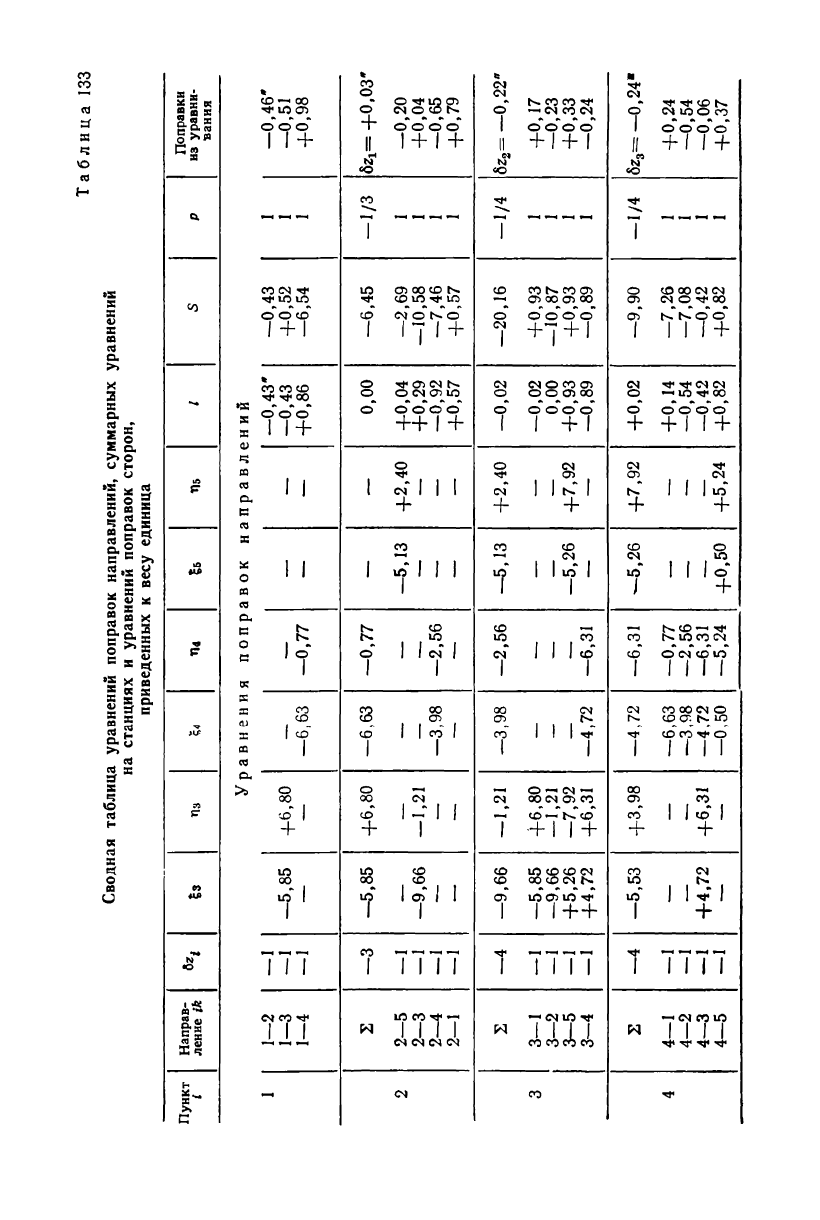
Таблица 109

Сводная таблица уравнений поправок направлений, суммарных уравнений

на

станциях

уравнений поправок сторон,

приведенных

весу единица

Пункт

Направ-

ление

Лэ 54

Л5

Поправки

из

уравни-

вания

Уравнения поправок направлений

1—2

1—3

1—4

— 1

—1

—5,85

+6,80

—6,63

—0,77

—

—0,43"

—0,43

+0,86

—0,43

+0,52

—6,54

—0,46"

—0,51

+0,98

—3

—5,85

+6,80

—6,63

—0,77

—

0,00

—6,45

-1/3

= +0,03"

2-5

2-3

2—4

2—1

—I

— 1

—1

—9,66

-1,21

—3,98 —2,56

—5,13

+2,40

+0,04

+0,29

—0,92

+0,57

—2,69

—10,58

—7,46

+0,57

—0,20

+0,04

—0,65

+0,79

—4

—9,66

-1.21

—3,98

—2,56

—5,13

+2,40

—0,02

—20,16

-1/4

= —0,22"

3—1

3—2

3—5

3—4

—1

— 1

—5,85

—9,66

+5,26

+4,72

+6,80

— 1,21

—7,92

+6,31

—4,72

—6,31

-5,26

+7,92

—0,02

0,00

+0,93

—0,89

+0,93

— 10,87

+0,93

—0,89

+0,17

—0,23

+0,33

—0,24

—4

—5,53

+3,98 —4,72

—6,31

—5,26

+7,92

+0,02 —9,90

-1/4

=: —0,24*

4—1

4—2

4—3

4-5

—1

+4J2

+6,31

—-6,63

—4,72

—0,50

—0,77

—2,56

—6,31

—5,24

+0>

+5>4

+0,14

—0,54

—0,42

+0,82

—7,26

—7,08

—0,42

+0,82

+0,24

—0,54

—0,06

+0,37

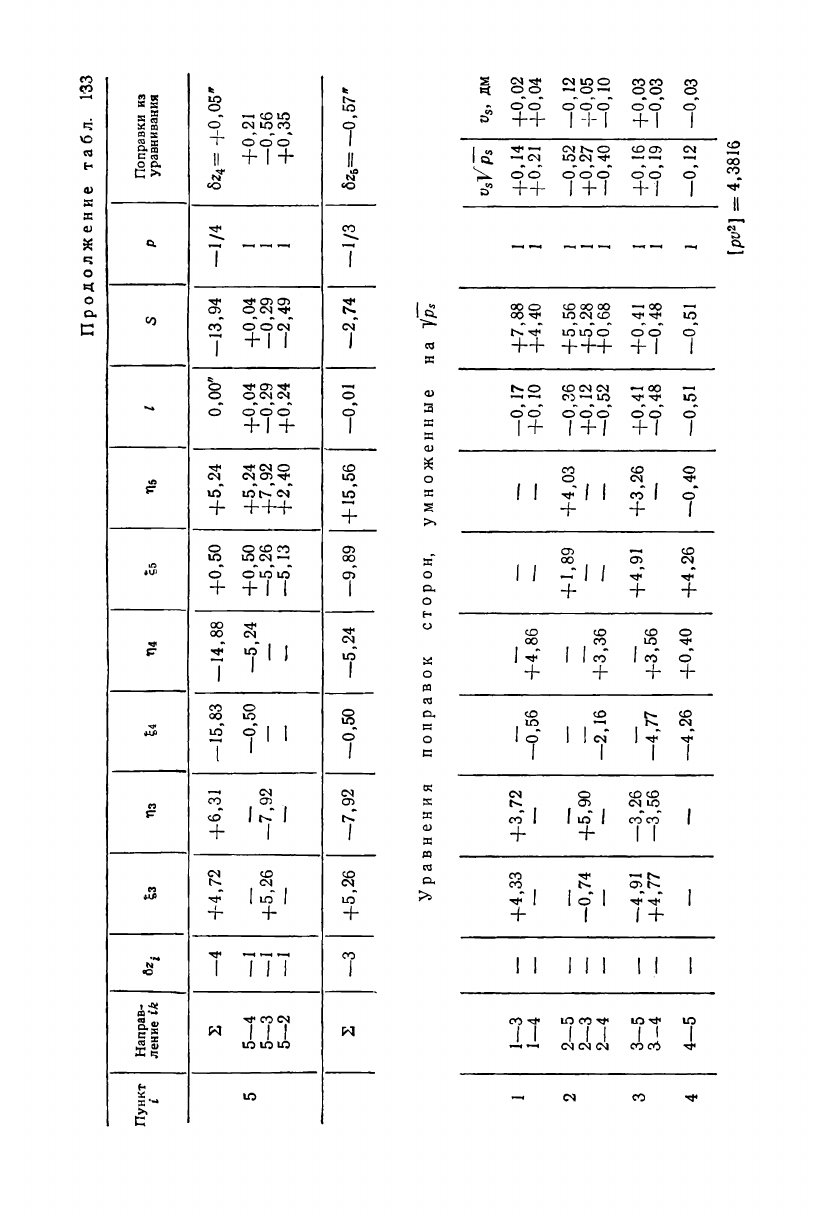
Продолжение табл.

ГЗЗ

Пункт

Направ-

ление

6z.

Т13

Т]4

С5

Л5

5 Р

Поправки

из

уравнивания

—4

+4,72

+6,31

— 15,83

— 14,88

+0,50 +5,24

0,00"

—13,94

-1/4

6г

= +0,05"

5-4

5-3

5—2

— 1

— I

— 1

+5,26

—7,92

—0,50

—5,24

+0,50

—5,26

—5,13

+5,24

+7,92

+2,40

+0,04

—0,29

+0,24

+0,04

-0,29

—2,49

+0,21

—0,56

+0,35

—3

+5,26

—7,92

—0,50

-5,24

—9,89

+ 15,56

—0,01

—2,74

-1/3

-0,57"

Уравнения поправок сторон,

умноженные

н a Ips

VsWs

, дм

1—3

1-4

—

+4,33

+3,72

—0,56

+4,86

—

—0,17

+0,10

+7,88

+4,40

+0,14

+0,21

+0,02

+0,04

2—5

2—3

2—4

—0,74 +5,90

-2,16

+3,36

+ 1,89

+4,03

-0,36

+0,12

—0,52

+5,56

+5,28

+0,68

—0,52

+0,27

—0,40

—0,12

+0,05

—0,10

3-5

а-4

—

—4,91

+4,77

—3,26

—3,56

-4>

+3,56

+4,91

+3,26

+0,41

—0,48

+0,41

—0,48

+0,16

-0,19

+0,03

—0,03

4-5

—

—4,26 +0,40

+4,26

—0,40

—0,51

\pv*} =

—0,12

4,3816

-0,03

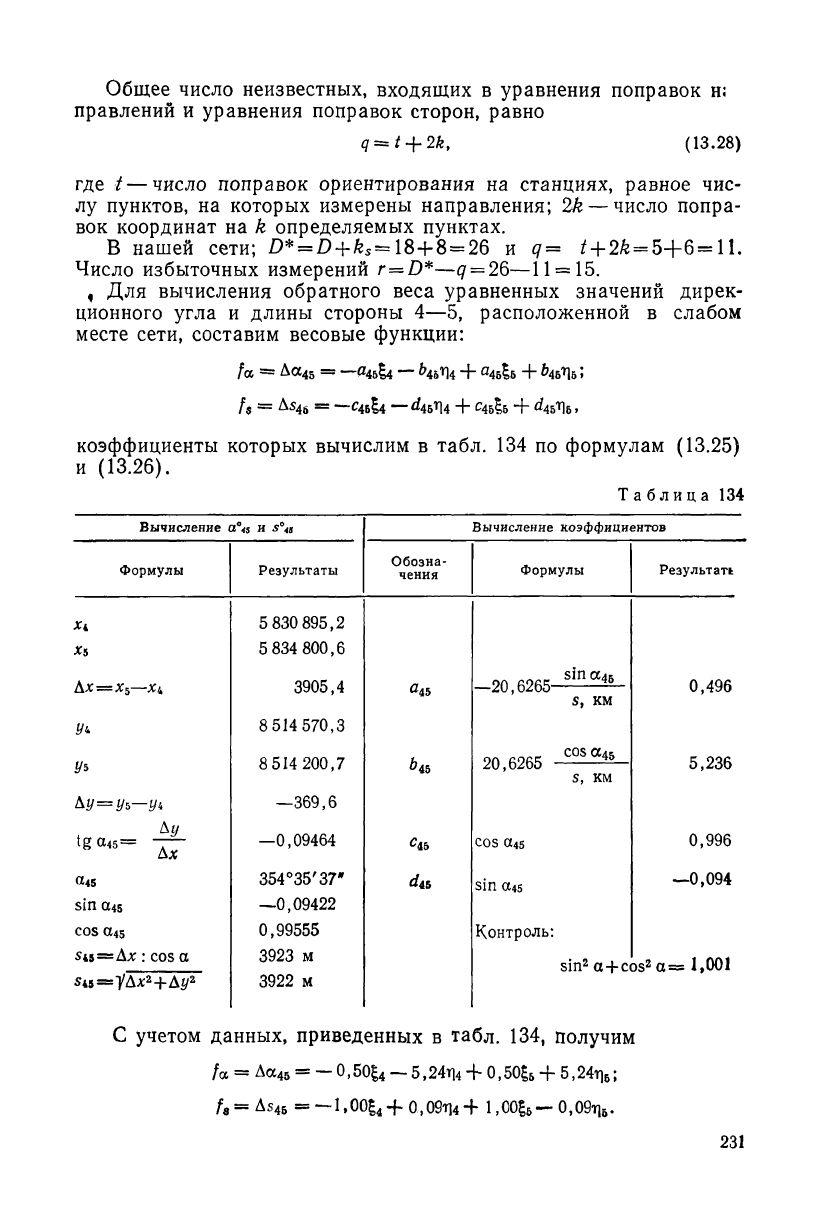
Общее число неизвестных, входящих в уравнения поправок н;

правлений и уравнения поправок сторон, равно

q = t + 2k, (13.28)

где t — число поправок ориентирования на станциях, равное чис-

лу пунктов, на которых измерены направления; 2k — число попра-

вок координат на k определяемых пунктах.

В нашей сети; D* = D + k

+ 8 = 26 и q= / +

2/г

= 5+6= 11.

Число избыточных измерений r=Z)*—q = 26—11 = 15.

, Для вычисления обратного веса уравненных значений дирек-

ционного угла и длины стороны 4—5, расположенной в слабом

месте сети, составим весовые функции:

fa = Да

=» -~045&4 — &4о*14

4б£б

Т]

;

®=

Л5

46 =

^46^4 — ^4бЛ4

С4ъ1ь

<*4ьПв»

коэффициенты которых вычислим в табл. 134 по формулам (13.25)

и (13.26).

Таблица 134

Вычисление а%s и

Формулы

Результаты

Вычисление коэффициентов

Обозна-

чения

Формулы

Результат!

5 830 895,2

Хь

5 834 800,6

3905,4

Уь

8 514 570,3

Уь

8 514 200,7

—369,6

Ъу

tga<

= —

—0,09464

«45

354°35'37*

sin a45

—0,09422

COS (X45 0,99555

545=Ax : cos a

3923 м

545=УДЛ:

+ДГ/

3922 м

Чь

Чъ

—20,6265-

20,6265

cos а

sin а45

Контроль:

sin а

4б

S, км

cos

s, км

0,496

5,236

0,996

—0,094

sin

а+cos

а= 1,001

С учетом данных, приведенных в табл. 134, получим

/ос = Л(Х45 - — 0,50|

- 5,24TU + 0,50£

+ 5,24г)

;

/в = As

= —l,00g

+0.,09T14+

,C0g

— 0,09t]

231

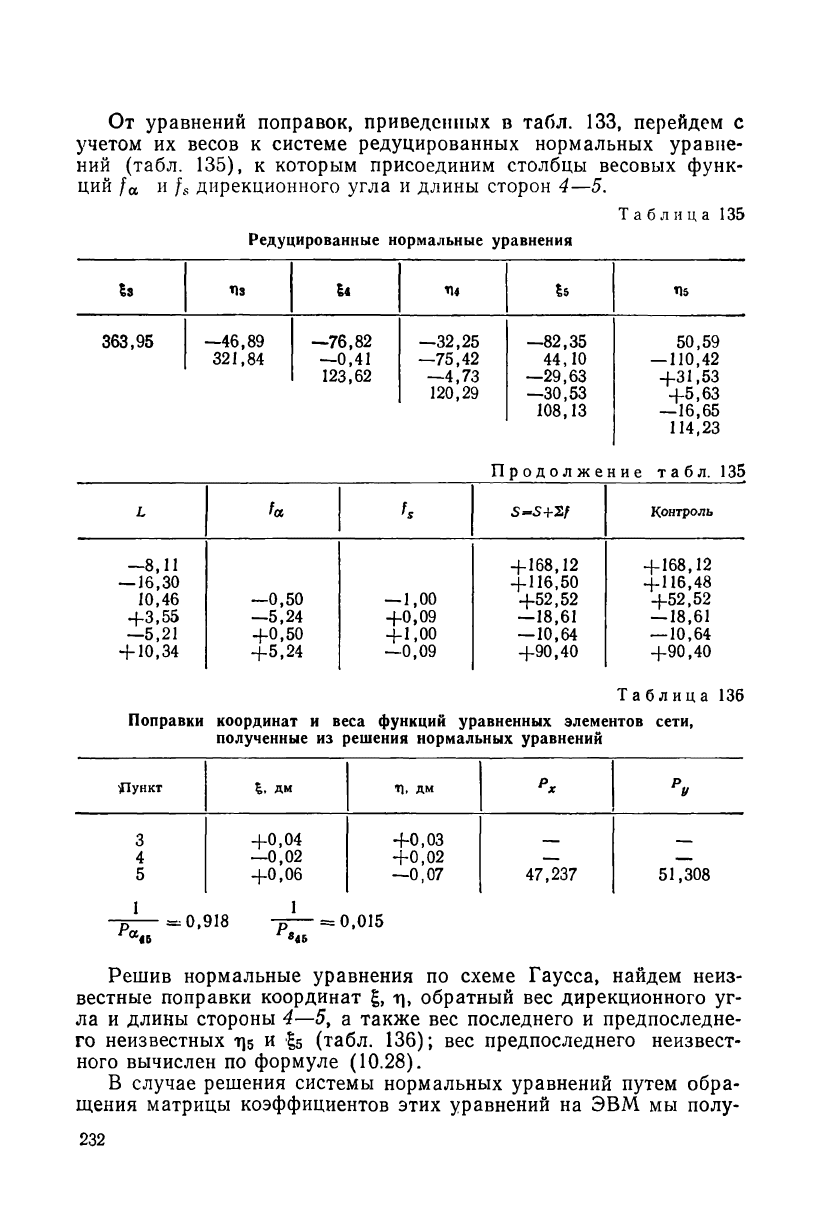
От уравнений поправок, приведенных в табл. 133, перейдем с

учетом их весов к системе редуцированных нормальных уравне-

ний (табл. 135), к которым присоединим столбцы весовых функ-

ций f

и f

дирекционного угла и длины сторон 4—5.

Таблица 135

Редуцированные нормальные уравнения

!з

Лз

Л5

363,95

—46,89

321,84

—76,82

•—0,41

123,62

—32,25

—75,42

—4,73

120,29

—82,35

44,10

—29,63

—30,53

108,13

50,59

—

110,42

+31,53

+5,63

—16,65

114,23

Продолжение табл. 135

Контроль

—8,11

—16,30

10,46

+3,55

—5,21

+ 10,34

—0,50

—5,24

+0,50

+5,24

— 1,00

+0,09

+1,00

—0,09

+ 168,12

+ 116,50

+52,52

—18,61

—10,64

+90,40

+168,12

+ 116,48

+52,52

— 18,61

— 10,64

+90,40

Таблица 136

Поправки координат и веса функций уравненных элементов сети,

полученные из решения нормальных уравнений

flyHKT дм

*Ъ Дм

+0,04

+0,03

—0,02

+0,02

—

5 +0,06 —0,07

47,237

51,308

Решив нормальные уравнения по схеме Гаусса, найдем неиз-

вестные поправки координат г\

обратный вес дирекционного уг-

ла и длины стороны 4—5, а также вес последнего и предпоследне-

го неизвестных т]5 и £5 (табл. 136); вес предпоследнего неизвест-

ного вычислен по формуле (10.28).

В случае решения системы нормальных уравнений путем обра-

щения матрицы коэффициентов этих уравнений на ЭВМ мы полу-

232

Элементы нсгоной матрицы Q

Лз

Л5

0,00747 —0,00101

0,00619

+0,00828

—0,00277

0,01895

+0,00416

+0,00261

+0,00486

0,01307

+0,00869

—0,00228

+0,01246

+0,00708

0,02117

—0,00550

+0,00673

—0,01000

—0,00027

—0,00675

0,01949

мим те же значения поправок координат, которые приведены в

табл. 136, и, кроме того, обратную матрицу Q весовых коэффи-

циентов (табл. 137), что позволит сделать оценку точности любых

элементов сети.

§ 76. Окончательные вычисления в линейно-угловой сети

Полученные из решения системы нормальных уравнений по-

правки дх= JQ Е и б у

— JQ rj,

переведенные в метры, прибавляют

к приближенным координатам определяемых пунктов у

) и

вычисляют окончательные значения координат (см. табл. 129)

х = +

= У°+&У-

В целях контроля уравнительных вычислений координаты оп-

ределяемых пунктов находят вторично, через их приращения Ах

и А у. С этой целью (см. табл. 133) вычисляют по формуле (10.24)

поправки bz ориентирования на станциях, а затем по формуле

(13.23) находят поправки Vik измеренных направлений. В этой же

таблице вычисляют по формуле (13.24) поправки сторон, умно-

женные на yp

, т. е. v*

=zv

yps, а затем и сами поправки

Урщ. (13.29)

выраженные в дециметрах. Значения величины Ур

берут из

табл. 132.

После исправления измеренных направлений и длин сторон

вычисленными поправками находят их уравненные значения

(табл. 138 и 139). Затем по уравненным углам, начиная от исход-

ной стороны сети, решают треугольники и вторично получают зна-

чения уравненных сторон (табл. 140). Расхождения в длинах од

них и тех же сторон, полученных из решения треугольников и пу-

тем введения поправок в измеренные расстояния, не должны пре-

вышать 1—3 единиц последнего знака после запятой, т. е. в на

шем случае 1—3 мм, что и соблюдается в табл. 140, в которую

записаны те и другие значения длин сторон.

233

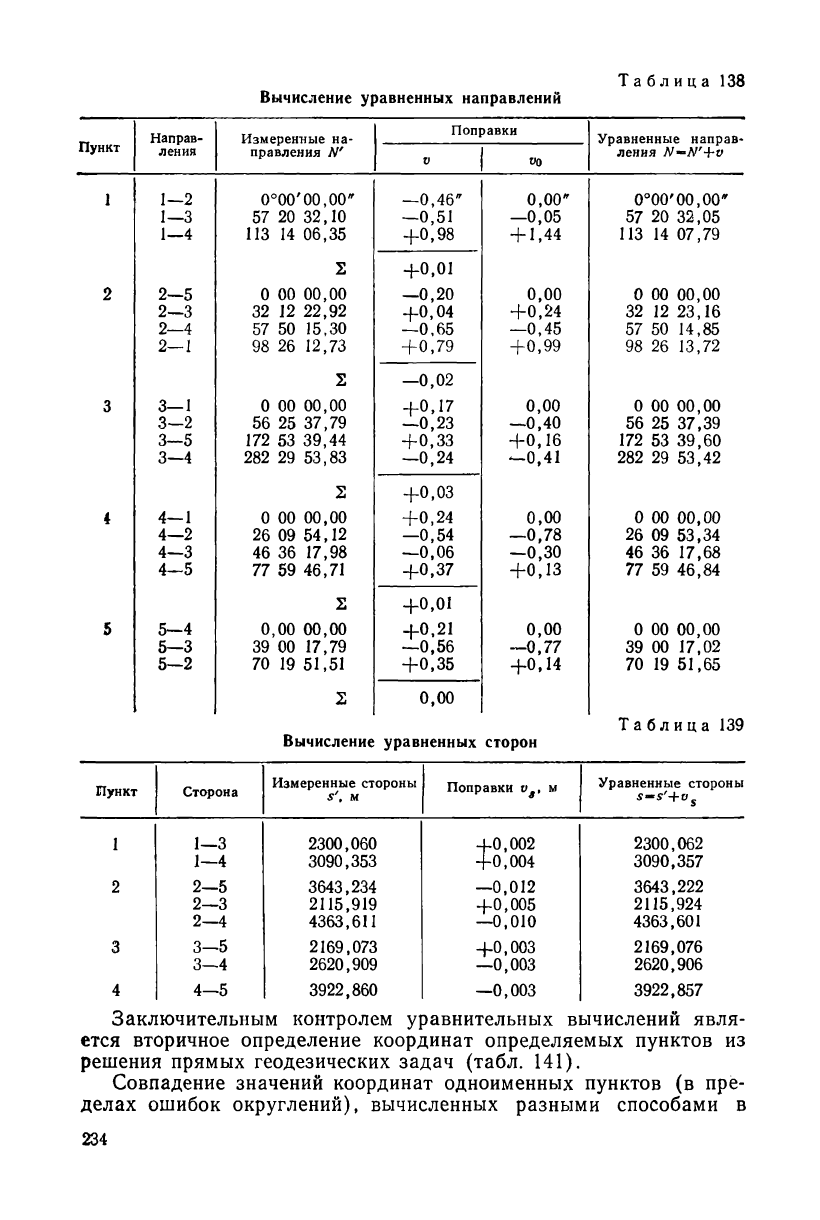
Вычисление уравненных направлений

Таблица

126

Таблица 127

Пункт

Направ-

ления

Измеренные на-

правления N'

Поправки

v vo

Уравненные направ-

ления JV—N'+v

1 1—2 0°00'00,00*

—0,46"

0,00"

OWOO.OO"

1—3 57 20 32,10

—0,51

—0,05

57 20 32,05

1—4

113 14 06,35 +0,98

+ 1,44

113 14 07,79

+0,01

2-5

0 00 00,00

—0,20

0,00

0 00 00,00

2-3

32 12 22,92

+0,04

+0,24

32 12 23,16

2—4 57 50 15,30

—0,65

—0,45

57 50 14,85

2—1

98 26 12,73

+0,79 +0,99

98 26 13,72

—0,02

3 3—1

0 00 00,00 +0,17 0,00

0 00 00,00

3—2

56 25 37,79 —0,23

—0,40

56 25 37,39

3-5

172 53 39,44

+0,33

+0,16

172 53 39,60

3—4

282 29 53,83

—0,24

—0,41

282 29 53,42

+0,03

4—1 0 00 00,00

+0,24

0,00

0 00 00,00

4—2

26 09 54,12

—0,54

—0,78

26 09 53,34

4—3

46 36 17,98

—0,06

—0,30

46 36 17,68

4-5

77 59 46,71

+0,37 +0,13

77 59 46,84

+0,01

5-4

0,00 00,00

+0,21

0,00 0 00 00,00

5—3 39 00 17,79

—0,56

—0,77 39 00 17,02

5-2

70 19 51,51

+0,35

+0,14

70 19 51,65

0,00

Таблица 139

Вычисление

уравненных сторон

Пункт

Сторона

Измеренные стороны

sм

Поправки v

, м

Уравненные стороны

s=s'+v

1—3

1—4

2300,060

3090,353

+0,002

+0,004

2300,062

3090,357

2 2—5

2—3

2—4

3643,234

2115,919

4363,611

—0,012

+0,005

—0,010

3643,222

2115,924

4363,601

3-5

3—4

2169,073

2620,909

+0,003

—0,003

2169,076

2620,906

4-5

3922,860

—0,003

3922,857

Заключительным контролем уравнительных вычислений явля-

ется вторичное определение координат определяемых пунктов из

решения прямых геодезических задач (табл. 141).

Совпадение значений координат одноименных пунктов (в пре-

делах ошибок округлений), вычисленных разными способами в

•234

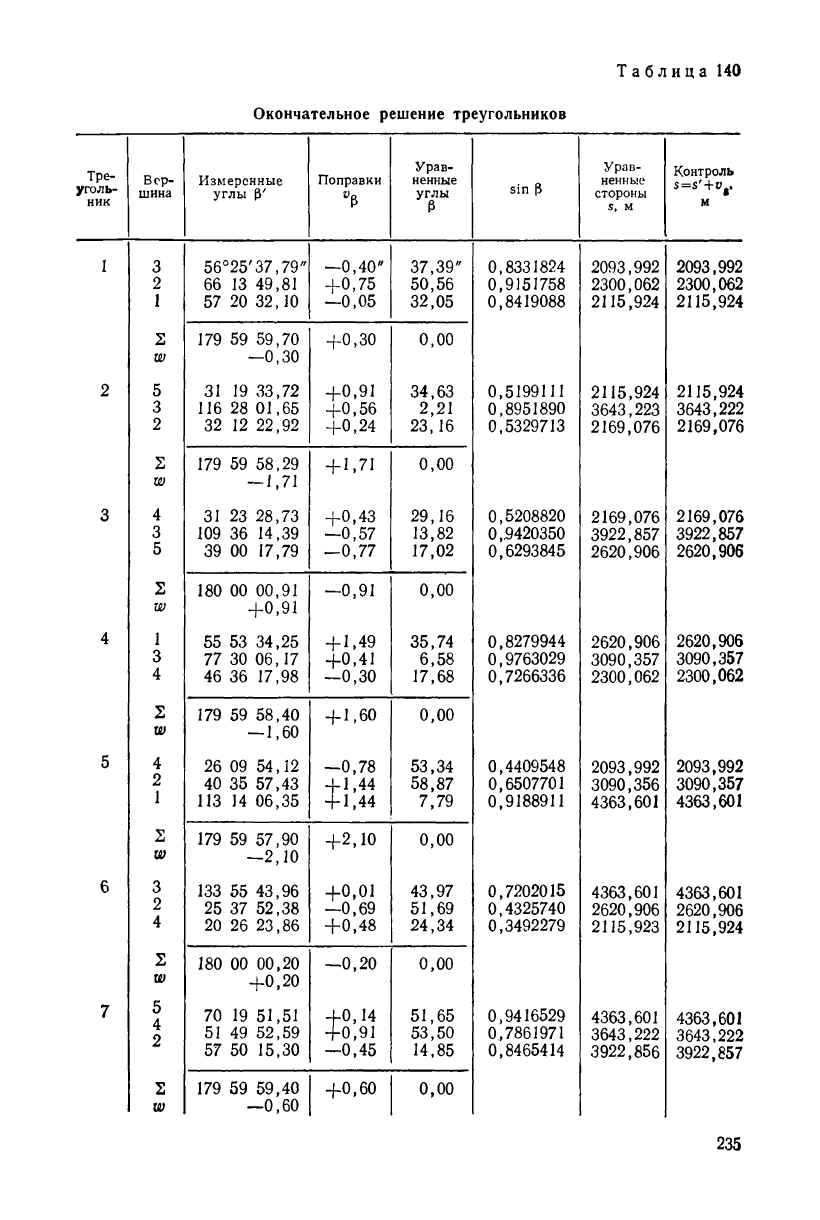
Таблица 126 Таблица

127

Окончательное решение треугольников

Тре-

уголь-

ник

Вер-

шина

Измеренные

углы

Поправки

Урав-

ненные

углы

sin р

Урав-

ненные

стороны

S, м

Контроль

s=s'+v

56°25'37,79"

66 13 49,81

57 20 32,10

—0,40"

+0,75

—0,05

37,39"

50,56

32,05

0,8331824

0,9151758

0,8419088

2093,992

2300,062

2115,924

2093,992

2300,062

2115,924

179 59

59,70

—0,30

+0,30

0,00

2 5

31 19

33,72

116 28 01,65

32 12

22,92

+0,91

+0,56

+0,24

34,63

2,21

23,16

0,5199111

0,8951890

0,5329713

2115,924

3643,223

2169,076

2115,924

3643,222

2169,076

ау

179 59

58,29

-1,71

+ 1,71

0,00

31 23

28,73

109 36 14,39

39 00 17,79

+0,43

—0,57

—0,77

29,16

13,82

17,02

0,5208820

,,9420350

0,6293845

2169,076

3922,857

2620,906

2169,076

3922,857

2620,906

180 00 00,91

+0,91

—0,91

0,00

55 53

34,25

77 30 06,17

46 36 17,98

+ 1,49

+0,41

—0,30

35,74

6,58

17,68

0,8279944

0,9763029

0,7266336

2620,906

3090,357

2300,062

2620,906

3090,357

2300,062

179 59

58,40

— 1,60

+ 1,60

0,00

26 09 54,12

40 35

57,43

113 14

06,35

—0,78

+ 1,44

53,34

58,87

7,79

0,4409548

0,6507701

0,9188911

2093,992

3090,356

4363,601

2093,992

3090,357

4363,601

179 59

57,90

—2,10

+2,10

0,00

6 3

133 55

43,96

25 37

52,38

20 26

23,86

+0,01

—0,69

+0,48

43,97

51,69

24,34

0,7202015

0,4325740

0,3492279

4363,601

2620,906

2115,923

4363,601

2620,906

2115,924

180 00

00,20

+0,20

—0,20

0,00

70 19 51,51

51 49

52,59

57 50 15,30

+0,14

+0,91

—0,45

51,65

53,50

14,85

0,9416529

0,7861971

0,8465414

4363,601

3643,222

3922,856

4363,601

3643,222

3922,857

179 59

59,40

—0,60

+0,60

0,00

•235

Таблица

126

Таблица

127

Контрольные вычисления окончательных координат

Формулы

k 3

Ci»

343°2Г4 2,18" 163°21'42,18"

40°42'14,23"

=fcpi

+57 20 32,05

—66 13 50,56

+55 53 35,74

aik

40 42 14,23

97 07 51,62

96 35 49,97

5 832 993,903

5 832 993,902

5 830 895,202

831

250,250

5 833 256,570

5 831250,250

kXik

+ 1743,653 —262,668

—355,048

cos a ik

0,7580894

—0,1241385

—0,1148888

Sik

2300,062

2115,924

3090,357

sin ш*

0,6521507

0,9922649

0,9933784

A yik

+ 1499,987

+2099,557

+3069,894

У1

8 511500,410 8 510 900,840

8511 500,410

Ук

8 513 000,397

8 514 570,304

Продолжение табл. 140

Формулы

Оисх

a ih

A x

cos а а

sin a ik

A yik

У%

220°42'14,23"

—77 30 06,58

143 12 07,65

5 830 895,202

5 832 993,902

—2098,700

—0,8007536

2620,906

0,5989939

+1569,907

8 513 000,397

8 514 570,304

97°07'51,62"

—32 12 23,16

64 55 28,46

5 834 800,608

5 833 256,570

+1544,038

0,4238110

3643,222

0,9057506

+32 299,851

8 510 900,840

8 514 200,691

277°07'5I,62"

116 28 02,21

33 35 53,83

5 834 800,607

5832 993,902

+1806,705

0,8329378

2169,076

0,5533666

+ 1200,294

513

000,397

8 514 200,691

табл. 129 и 141, указывает на правильность уравнительных вычис-

лений. За окончательные координаты принимают их значения, при-

веденные в табл. 129, которые и записывают в каталог координат.

§ 77. Оценка точности уравненных элементов сети

Средняя квадратическая ошибка единицы веса (уравненного

направления) вычисляется по формуле

l/^pu

" if 4,3816

К —7— = К [5 ^ 0,54 ,

где число избыточных измерений равно —q~D+k

—/—2k =

= 18+8—5—6=15.

Взяв из табл. 136 значения обратных весов 1 JP

и l/P

най-

•236

дем средние квадратические ошибки дирекционного угла и длины

стороны 4—5:

т<х

= ц = 0,54 /0,918 = 0,52";

= 0,54 /МТ5 =- 0,07 дм = 0,007 м.

= Р у -JT

Средние квадратические ошибки определения координат пунк-

та 5 найдем с учетом весов в табл. 136 по формулам

ji 0,54

VP*

/47\237

0,54

517308

= 0,08 дм «0,008 м;

= 0,08 дм = 0,008 м;

Мь

Таблица 142

= /0,000128 = 0,011 м.

В том случае, когда система нормальных уравнений поправок

координат решается путем ее обращения с вычислением обратной

матрицы Q весовых коэффициентов, представляется возможность

вычислить средние квадратические ошибки любого уравненного

элемента сети, а не только тех, для

которых в случае решения уравне-

ний по схеме Гаусса составляются

весовые функции. В самом деле, ис-

пользуя диагональные элементы ве-

совой матрицы Q, приведенной для

нашей сети в табл. 137, можно вы-

числить по формуле

™х

)У

= \i У Он

средние квадратические ошибки абсцисс и ординат всех опреде-

ляемых пунктов (табл. 142).

Средние квадратические ошибки дирекционного угла и длины

любой стороны (диагонали) sik

соединяющей смежные или разде-

ленные рядом треугольников пункты i и k, при использовании эле-

ментов весовой матрицы Q вычисляют по формуле

Пункт

M-Vm*

+mi

0,005

0,004

0,006

0,007

0,006

0,009

0,008

0,011

, = 11 Y-J7 /f'a

sOfa

(13.30)

ПО

Обратный вес оцениваемого элемента шл или sik найдем

формуле

= (13.31)

где транспонированные по отношению к f^fa и f=f

векторы-стро-

ки коэффициентов весовых функций дирекционного угла aik и дли-

ны стороны Sik равны соответственно

Г a f*a

= (—a

— b

k aik bik); ]

/% = f*t

(—^k — dik c

k dik). J

(13.32)

237

Здесь коэффициенты aik, bi

вычисляют по формулам (13.25)»

a cik и dik — по формулам (13.26), используя в обоих случаях при-

ближенные координаты пунктов на концах оцениваемой стороны

(диагонали) Si

Матрица Qi-

формируется из тех элементов общей для сети

матрицы Q весовых коэффициентов, которые соответствуют коор-

динатам Xi, ijiy Xky уь начала и конца оцениваемой стороны (диаго-

нали) Siky и записывается в виде

В качестве примера вычислим по формулам (13.31) — (13.33)

обратный вес уравненных значений дирекционного угла и длины

стороны 4—5, а также диагонали 1—5, соединяющей несмежные

пункты, один из которых является исходным, что надо иметь в ви-

ду при составлении весовых функций, опуская в выражениях

(13.32) коэффициенты при координатах исходного пункта, так как

поправки координат исходного пункта равны нулю.

Для обратного веса дирекционного угла и длины стороны 4—5

в соответствии с формулой (13.31) напишем в общем виде

Подставив в (13.34) и (13.35) числовые значения соответствуют

щих коэффициентов из табл. 134 и 137, получим:

для дирекционного угла стороны 4—5

(13.33)

1/Лх

(—СГ

—

&45

45 Ь

4ь

) х

\ /—«45

(13.34)

(13.35)

1/Лх

« (-0,50 —5,24 0,50 5,24) X

' 0,01895 0,00486 "

0,00486 0,01307

0,01246 0,00708

—0,01000 —0,00027 —

238