Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

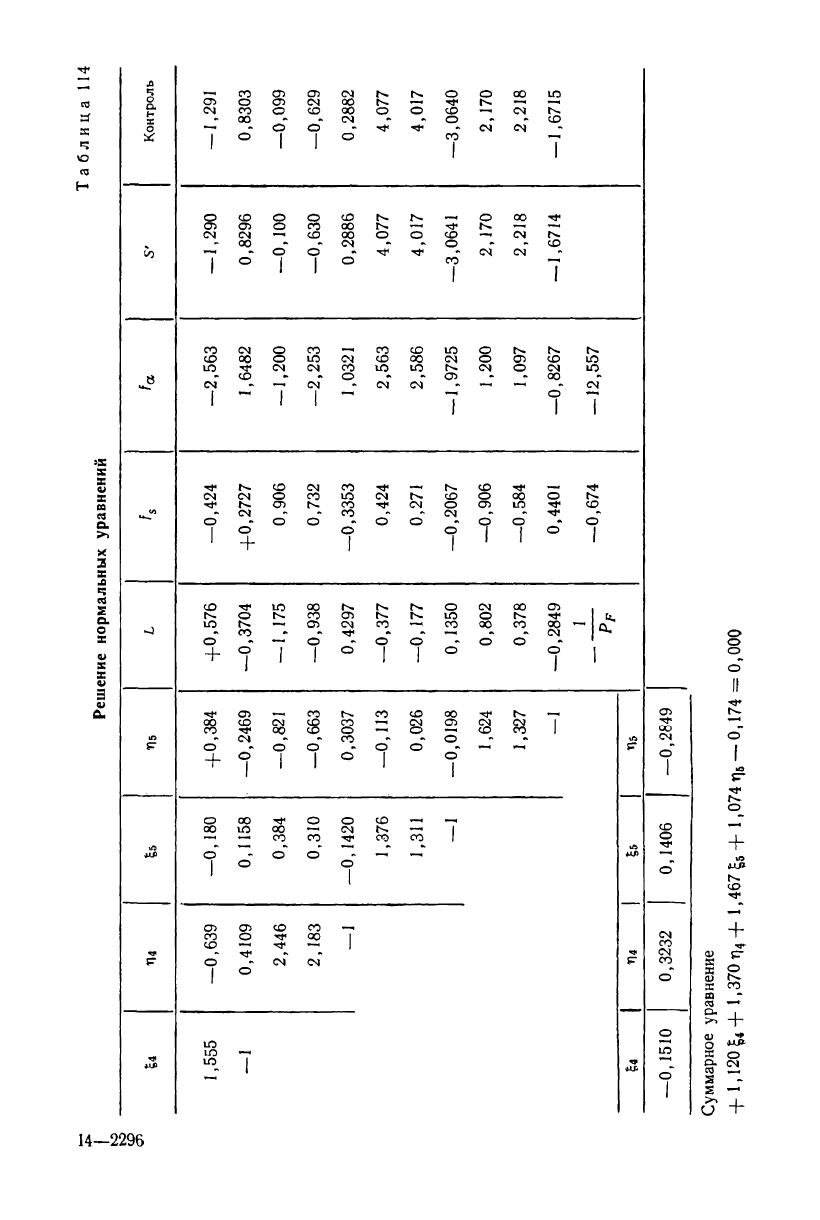
Таблица 109

Решение нормальных уравнений

"П4

Ь Л5

Контроль

1,555

—0,639

—0,180

+0,384 +0,576 —0,424

—2,563

— 1,290

—

1,291

—1

0,4109

0,1158 —0,2469

—0,3704 +0,2727

1,6482

0,8296

0,8303

2,446

0,384

—0,821

—1,175 0,906

-1,200 —0,100

—0,099

2,183

0,310

—0,663 —0,938 0,732

—2,253 —0,630 —0,629

— 1

—0,1420 0,3037

0,4297

—0,3353

1,0321

0,2886

0,2882

1,376

—0,113

—0,377 0,424

2,563 4,077

4,077

1,311

0,026

—0,177

0,271

2,586

4,017

— 1

—0,0198 0,1350

—0,2067

— 1,9725 —3,0641

—3,0640

1,624

0,802

—0,906

1,200

2,170

1,327

0,378

—0,584

1,097

2,218

— 1

—0,2849

~ PF

0,4401

—0,674

—0,8267

— 12,557

—1,6714

—1,6715

£4

Л4

1 15

—0,1510

0,3232

0,1406 —0,2849

Суммарное уравнение

+ 1,120 k + 1,370

т}

1,467|

+ 1,074 ^ — 0,174 =

0,000

114 составлено суммарное уравнение. Подставив в него найденные

поправки г), получим

—0,169 + 0,443+ 0,206 —0,306 — 0,174 = 0,000,

что свидетельствует о правильности решения данной системы

уравнений.

Поправки координат £ и т] надо выразить в метрах

БЛ;=5Г

~"ПГ&' ^ = ^

и затем вычислить окончательные координаты определяемых пунк-

тов (см. табл. 108) по формулам

Xi = + yi = y°i + by

§ 69 Вычисление уравненных сторон и углов треугольников.

Контрольные вычисления окончательных координат

Полученные из решения нормальных уравнений поправки коор-

динат

и т] подставляют в формулу (12.4) и вычисляют поправки

Vik (в дециметрах) к длинам s'ik измеренных сторон (см. табл.

111). Затем эти поправки выражают в метрах, исправляют ими

Таблица 115

Вычисление уравненных сторон трилатерации

Сторона (i-k)

Измеренные стороны

на плоскости

'ik•

Поправки v из уравнивания

Уравненные стороны

'ik+

ik•

Сторона (i-k)

Измеренные стороны

на плоскости

'ik•

дм

Уравненные стороны

'ik+

ik•

4.1

4.2

4.3

4.5

5.1

5.2

6275,170

6112,590

6723,850

7287,570

5485,040

6326,160

0,25

0,24

0,14

—0,16

0,14

0,15

0,025

0,024

0,014

—0,016

0,014

0,015

6275,195

6112,614

6723,864

7287,554

5485,054

6326,175

измеренные стороны и получают их уравненные значения (табл.

115) по формуле

Sik = s'ik +

Vik-

Используя уравненные стороны, вычисляют уравненные углы

всех треугольников по теореме косинуса угла

+ с

— 2bccosA.

Применительно к нашей сети в табл. 116 вычислены уравнен-

ные углы только в тех треугольниках, углы и длины сторон кото-

рых использованы для вычисления приращений координат опре-

деляемых пунктов.

Заключительным контролем уравнительных вычислений являет-

ся повторное вычисление окончательных координат определяемых

пунктов по другому способу, например путем решения прямых гео-

дезических задач по формулам (7.7).

210

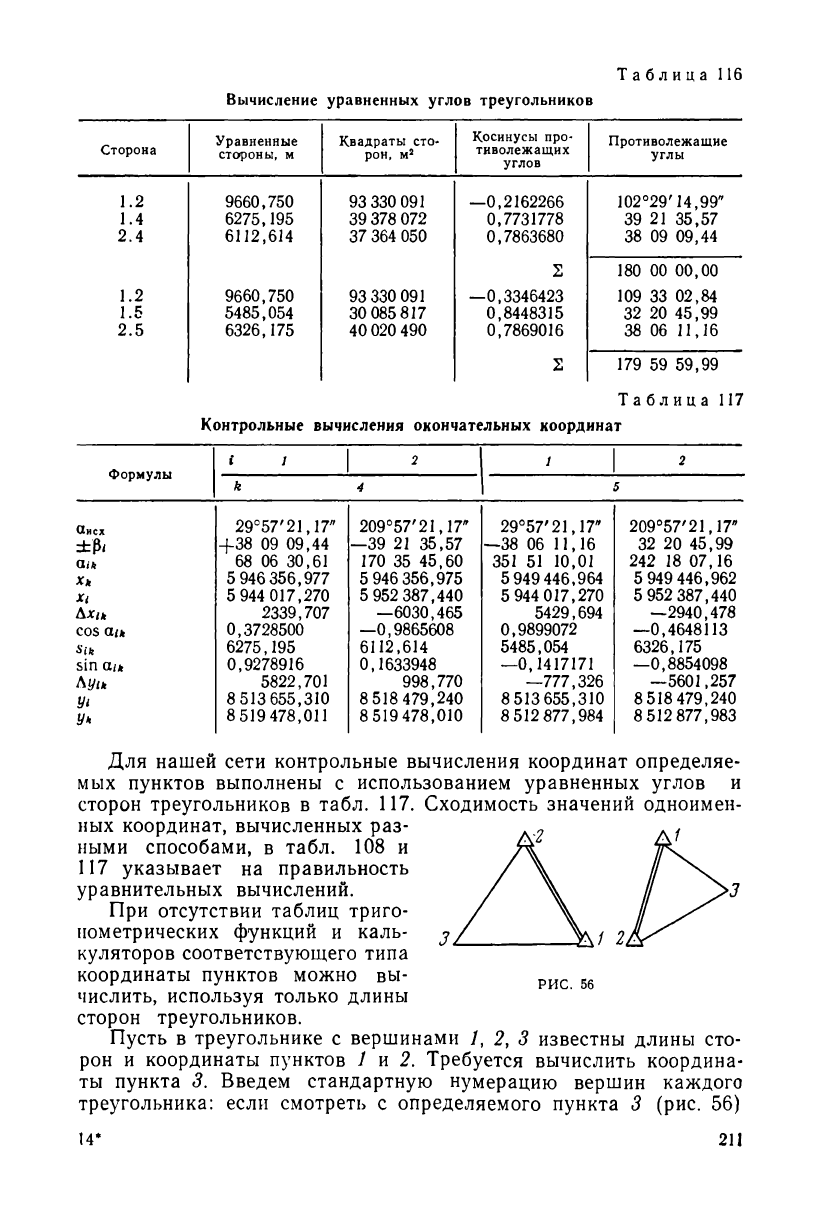
Таблица

109

Вычисление уравненных углов треугольников

Сторона

Уравненные

стороны, м

Квадраты сто-

рон, м

Косинусы про-

тиволежащих

углов

Противолежащие

углы

1.2

1.4

2.4

9660,750

6275,195

6112,614

330 091

39 378

072

37 364 050

—0,2162266

0,7731778

0,7863680

102°29'14,99"

39 21 35,57

38 09 09,44

180 00 00,00

1.2

1.5

2.5

9660,750

5485,054

6326,175

93 330

091

085

817

40 020

490

—0,3346423

0,8448315

0,7869016

109 33 02,84

32 20 45,99

38 06 11,16

179 59 59,99

Таблица 117

Контрольные вычисления окончательных координат

Формулы

i 1

Формулы

(Хисх

Шк

A x

cos aik

sin a ik

Л yik

У1

Ун

29°57'21,17"

+38 09 09,44

68 06 30,61

5 946 356,977

5 944 017,270

2339,707

0,3728500

6275,195

0,9278916

5822,701

8513655,310

8519478,011

209°57'21,17"

—39 21 35,57

170 35 45,60

5 946 356,975

5 952 387,440

—6030,465

—0,9865608

6112,614

0,1633948

998,770

8 518 479,240

8519478,010

29°57'21,17"

—38 06 11,16

351 51 10,01

5949 446» 964

5 944 017,270

5429,694

0,9899072

5485,054

—0,1417171

—777,326

8513655,310

8 512 877,984

209°57'21

17*

32 20 45,99

242 18 07,16

5 949 446,962

5 952 387,440

—2940,478

—0,4648113

6326,175

—0,8854098

—5601,257

8 518 479,240

8 512 877,983

Для нашей сети контрольные вычисления координат определяе-

мых пунктов выполнены с использованием уравненных углов и

сторон треугольников в табл. 117. Сходимость значений одноимен-

ных координат, вычисленных раз-

ными способами, в табл. 108 и

117 указывает на правильность

уравнительных вычислений.

При отсутствии таблиц триго-

нометрических функций и каль-

куляторов соответствующего типа

координаты пунктов можно вы-

числить, используя только длины

сторон треугольников.

Пусть в треугольнике с вершинами /, 2, 5 известны длины сто-

рон и координаты пунктов 1 и 2. Требуется вычислить координа-

ты пункта 3. Введем стандартную нумерацию вершин каждого

треугольника: если смотреть с определяемого пункта 3 (рис. 56)

РИС. 56

14*

211

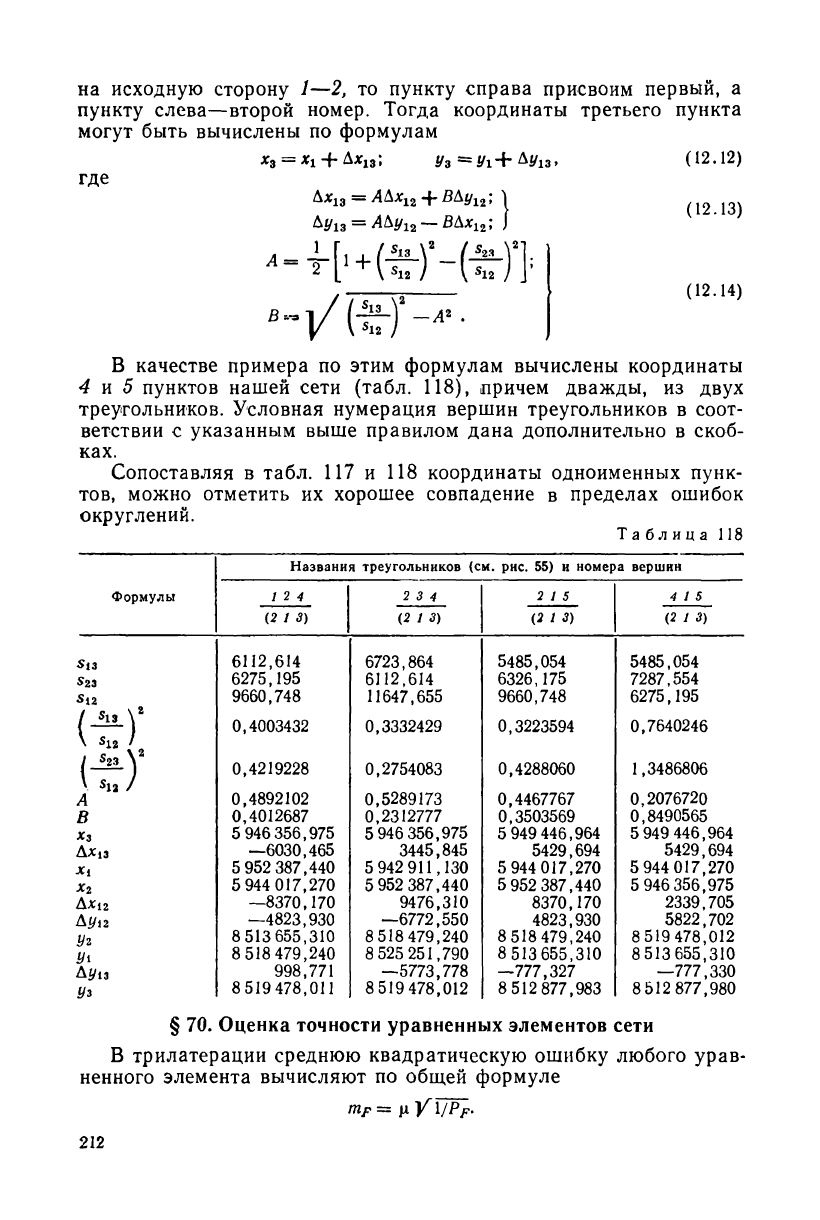
на исходную сторону 1—2, то пункту справа присвоим первый, а

пункту слева—второй номер. Тогда координаты третьего пункта

могут быть вычислены по формулам

*з =

Д*1з;

Уз = Уг+

^У13 >

где

Дх

= ААх

+ ВАу

; |

, = — БДдсг

; J

(12.12)

(12.13)

'-rHt-H-S-r]'

(12.14)

В качестве примера по этим формулам вычислены координаты

4 и 5 пунктов нашей сети (табл. 118), причем дважды, из двух

треугольников. Условная нумерация вершин треугольников в соот-

ветствии с указанным выше правилом дана дополнительно в скоб-

ках.

Сопоставляя в табл. 117 и 118 координаты одноименных пунк-

тов, можно отметить их хорошее совпадение в пределах ошибок

округлений.

Таблица 118

Формулы

Названия треугольников (см. рис. 55) и номера вершин

1 2 4 2 3 4

2 1 5

4 1 5

(2 1 3)

. (2 1 3)

(2 t 3)

(2 1 3)

6112,614

6275,195

9660,748

6723,864

6112,614

11647,655

5485,054

6326,175

9660,748

5485,054

7287,554

6275,195

0,4003432 0,3332429

0,3223594

0,7640246

0,4219228

0,2754083

0,4288060 1,3486806

0,4892102

0,4012687

5 946 356,975

—6030,465

5 952 387,440

5 944 017,270

—8370,170

—4823,930

8513655,310

8 518 479,240

998,771

8519478,011

0,5289173

0,2312777

5 946 356,975

3445,845

5 942 911,130

5 952 387,440

9476,310

—6772,550

8 518 479,240

8 525 251,790

—5773,778

8519478,012

0,4467767

0,3503569

5 949 446,964

5429,694

5 944 017,270

5 952 387,440

8370,170

4823,930

8 518 479,240

8 513655,310

—777,327

8 512 877,983

0,2076720

0,8490565

5 949 446,964

5429,694

5 944 017,270

5 946 356,975

2339,705

5822,702

8519478,012

8513655,310

—777,330

8 512 877,980

$23

(—)*

, s

(t)

Хз

Д*13

Ay 12

Уг

У1

А£/1з

Уз

§ 70. Оценка точности уравненных элементов сети

В трилатерации среднюю квадратическую ошибку любого урав-

ненного элемента вычисляют по общей формуле

vVWf-

212

Обратный вес оцениваемой функции F находят либо в процессе

решения нормальных уравнений по схеме Гаусса, либо путем об-

ращения матрицы коэффициентов этих уравнений.

Среднюю квадратическую ошибку единицы веса вычисляют по

формуле

где v — поправки к измеренным с весами р величинам, г — число

избыточных измерений, определяемое по формуле

r = N* —2k,

в которой N* = k

+ k

—общее число всех измеренных в сети ве-

личин: сторон (k

) и азимутов (k

). В это число не входят сторо-

ны и дирекционные углы (азимуты) между исходными пунктами;

2k— число неизвестных поправок координат, равное удвоенному

числу определяемых пунктов.

В нашей сети £ = 2, = k

=0, [pv

] =0,213.

По этим данным получим

ц = /0,213/(6—2x2) = 0,33 дм.

Взяв из табл. 114 обратный вес стороны 4—5 (\/P

= 0,674) и

обратный вес ее дирекционного угла (!/Р<х =12,557), найдем сред-

ние квадратические ошибки

S45

= 0,33 /07674 = 0,27 дм = 0,027 м;

та

« 0,33/12,557= 1,17\

Для вычисления средней квадратической ошибки определения

координат какого-либо пункта, например пункта 5, необходимо

неизвестные поправки координат этого пункта § и rj поставить со-

ответственно на предпоследнее и последнее место в системе нор-

мальных уравнений.

Вес последнего неизвестного равен коэффициенту при ц в по-

следнем преобразованном нормальном уравнении. В нашем случае

из табл. 114 решения системы нормальных уравнений для пункта

5 находим Ру

= Рг\

=1,327.

Вес предпоследнего неизвестного Рх

~Ръ

найдем по формуле

(10.28)

= Р

Уъ W ~

1,327

0 0262" = 1,310.

C+-J- 1.327Н ГУзГр

С вычисленными значениями весов = 1,310 и Ру

= 1,327

найдем средние квадратические ошибки определения координат

пункта 5 в уравненной сети трилатерации

Хъ

= ц VVK

= 0,33/1/1,310 = 0,29 дм

0,029 м;

Уъ Р УЩ* ~ °'

327

= °>

ДМ

= 0,029 м;

= Vm

* +/0,29

+0,29* = 0,41 дм = 0,041 м.

213

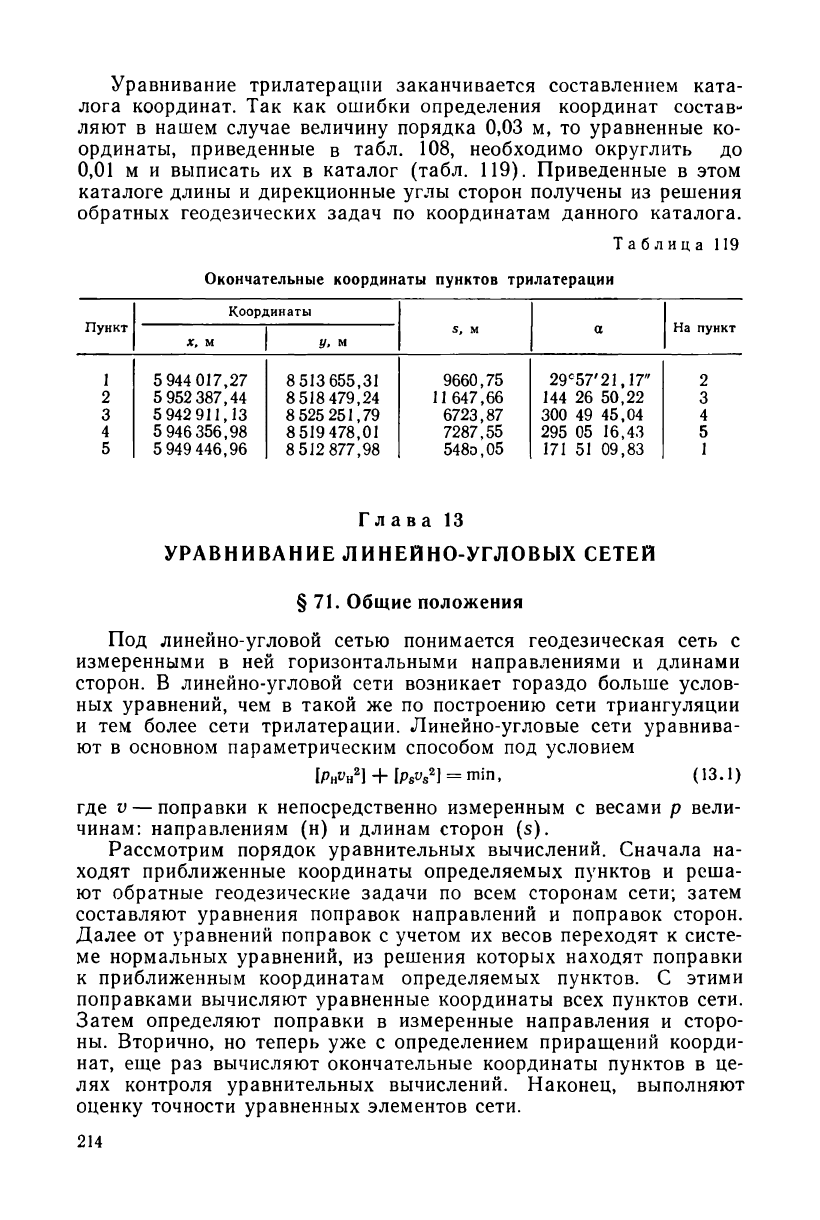
Уравнивание трилатерации заканчивается составлением ката-

лога координат. Так как ошибки определения координат состав-

ляют в нашем случае величину порядка 0,03 м, то уравненные ко-

ординаты, приведенные в табл. 108, необходимо округлить до

0,01 м и выписать их в каталог (табл. 119). Приведенные в этом

каталоге длины и дирекционные углы сторон получены из решения

обратных геодезических задач по координатам данного каталога.

Таблица 119

Окончательные координаты пунктов трилатерации

Пункт

Координаты

х, м у, м

S, м

Ha пункт

1 5 944 017,27

8513655,31

9660,75

57'21,17"

5 952 387,44

8 518 479,24

11 647,66

144 26 50,22 3

5 942 911,13 8 525 251,79

6723,87

300 49 45,04

5 946 356,98

8519478,01

7287,55

295 05 16,43

5 949 446,96

8 512 877,98

548э,05

171 51 09,83

Глава 13

УРАВНИВАНИЕ ЛИНЕЙНО-УГЛОВЫХ СЕТЕЙ

§ 71. Общие положения

Под линейно-угловой сетью понимается геодезическая сеть с

измеренными в ней горизонтальными направлениями и длинами

сторон. В линейно-угловой сети возникает гораздо больше услов-

ных уравнений, чем в такой же по построению сети триангуляции

и тем более сети трилатерации. Линейно-угловые сети уравнива-

ют в основном параметрическим способом под условием

[/W] + [p^ = niin, (13.1)

где v — поправки к непосредственно измеренным с весами р вели-

чинам: направлениям (н) и длинам сторон (s).

Рассмотрим порядок уравнительных вычислений. Сначала на-

ходят приближенные координаты определяемых пунктов и реша-

ют обратные геодезические задачи по всем сторонам сети; затем

составляют уравнения поправок направлений и поправок сторон.

Далее от уравнений поправок с учетом их весов переходят к систе-

ме нормальных уравнений, из решения которых находят поправки

к приближенным координатам определяемых пунктов. С этими

поправками вычисляют уравненные координаты всех пунктов сети.

Затем определяют поправки в измеренные направления и сторо-

ны. Вторично, но теперь уже с определением приращений коорди-

нат, еще раз вычисляют окончательные координаты пунктов в це-

лях контроля уравнительных вычислений. Наконец, выполняют

оценку точности уравненных элементов сети.

214

При уравнивании линейно-угловых сетей очень важно правиль-

но установить соотношение весов измеренных направлений и длин

сторон. В общем случае вес измеренного элемента вычисляется по

формуле

где jli — средняя квадратическая ошибка единицы веса, т/ — сред-

няя квадратическая ошибка измерения /-го элемента.

Выбор постоянной с=ц

до некоторой степени произволен и на-

правлен на удобства вычислений. Приняв

jj.

= tn^ const, (13.3)

где т

— средняя квадратическая ошибка измерения направле-

ний в сети, получим формулы для вычисления весов измеренных

направлений и сторон

Рн=1; Ps =

/Щ

, (13.4)

где m

— средняя квадратическая ошибка измерения сторон.

От того, насколько надежно будет установлено в (13.4) отно-

шение квадратов ошибок угловых и линейных измерений, зависит

достоверность результатов уравнивания сети. Поэтому вопросам

надежного определения величины средних квадратических ошибок

и m

в линейно-угловой сети должно быть уделено самое серь-

езное внимание, причем как на стадии проектирования сети, так и

на стадии постановки и исполнения угловых и линейных измере-

ний в ней.

Точность определения величины средней квадратической ошиб-

ки измеренных углов и направлений по невязкам треугольников

тем выше, чем больше в сети треугольников с измеренными угла-

ми. Для определения этих ошибок с погрешностями порядка

= 0,l m, 0,15 m" и 0,2 m" требуется, чтобы число невязок тре-

угольников в сети было соответственно не менее 50, 25 и 15. Это

вытекает из расчетов по формуле (8.5).

Величина средней квадратической ошибки измерения сторон

светодальномерами зависит при прочих равных условиях от длин

сторон s и в первом приближении вычисляется по эмпирическим

формулам вида

= (13.5)

или т

= а

+ a

s -f a

, (13.6)

где коэффициенты а,- находятся из обработки результатов измере-

ний светодальномером эталонных базисов разной длины s или

по свободным членам условных уравнений трилатерации, в кото-

рой стороны разной длины измерены одним и тем же светодально-

мером. Для каждого экземпляра светодальномера даже одного и

того же типа коэффициент at в формулах (13.5) или (13.6) долж-

ны определяться отдельно.

215

Вес измеренных сторон в линейно-угловой сети нередко вычис-

ляют по формуле

(13.7)

в основе которой лежит предположение, что в процессе угловых и

линейных измерений для каждой конкретной стороны реализуется

равенство

т" m

= (13.8)

В процессе полевых измерений условие (13.8) не выполняется,

поэтому формула (13.7) дает неправильное представление о реаль-

ных весах измеренных сторон.

В целях установления более или менее достоверного соотноше-

ния весов измеренных направлений и сторон в линейно-угловой

сети, особенно когда она невелика по размерам, сеть уравнивают

в три этапа. Сначала как угловую с равноточно измеренными на-

правлениями; затем как линейную и, наконец, как линейно-угло-

вую. На первом этапе сеть рассматривают как свободную и из

уравнивания находят среднюю квадратическую ошибку единицы

веса ijuiH, т. е. ошибку направления. На втором этапе, при уравни-

вании только линейных измерений, веса измеренных сторон при-

нимают обратно пропорциональными квадратам их длин, выра-

женных в километрах, и затем из уравнивания сети получают

среднюю квадратическую ошибку единицы веса [x

на 1 км рас-

стояния. Вес каждой измеренной стороны находят по формуле

(13.9)

Приняв веса измеренных направлений равными единице (р

= 1) и вычислив веса сторон по формуле (13.9), окончательно

уравнивают линейно-угловую сеть за все возникающие в ней гео-

метрические условия. Данный путь установления весов измерен-

ных сторон дает удовлетворительные результаты и нередко исполь-

зуется при уравнивании сетей, создаваемых, например, на геоди-

намических полигонах.

§ 72. Апробирование результатов угловых и линейных измерений

Методику уравнивания линейно-угловой триангуляции рассмот-

рим на примере небольшой сети (рис. 57), в которой в качестве

исходных элементов заданы на плоскости координаты пунктов /

л 2 или, что все равно, координаты пункта /, длина и дирекцион-

ный угол исходной стороны 1—2 (табл. 120).

Прежде чем приступить к собственно уравниванию сети, вы-

полняют предварительные вычисления. Обработка угловых изме-

рений в линейно-угловой сети на этой стадии вычислений ведется

подобно тому, как это делается в триангуляции, а обработка ли-

нейных измерений так же, как в трилатерации. Поскольку методи-

216

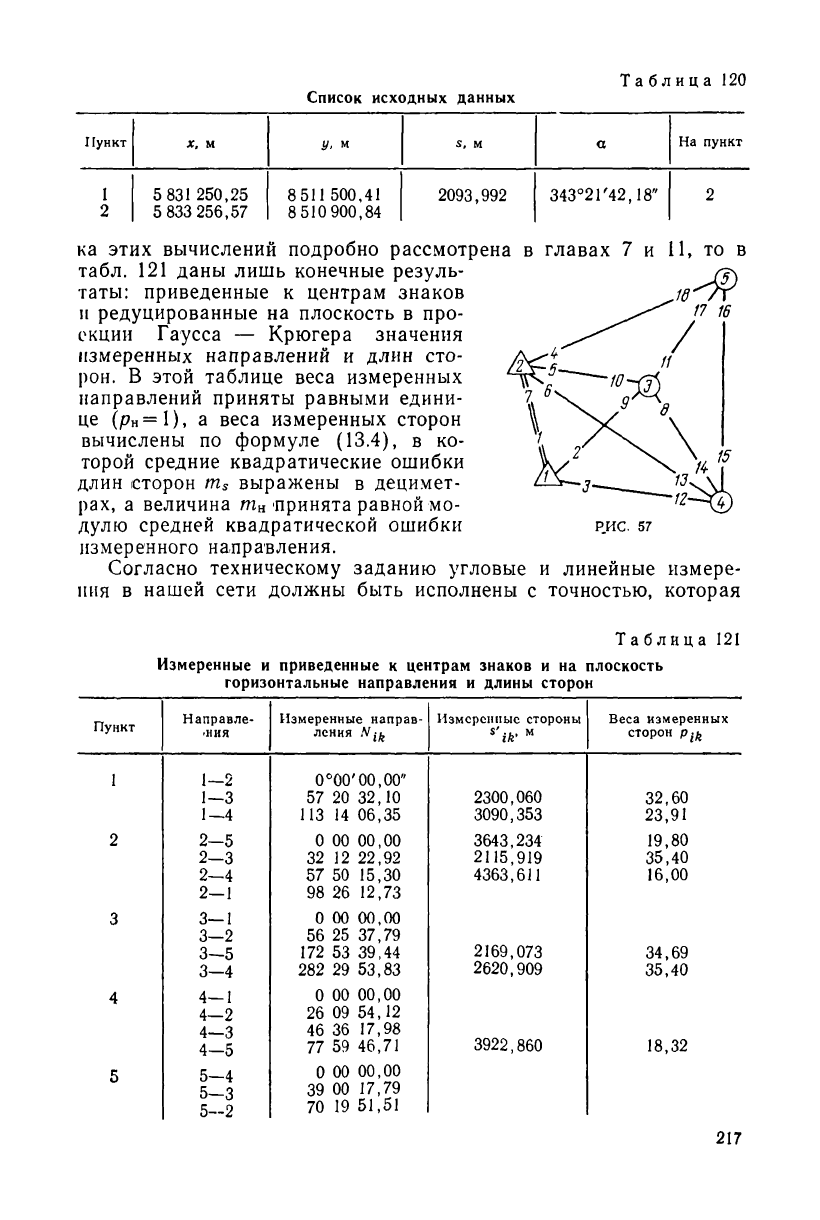
Таблица

126

Таблица 127

Список исходных данных

Пункт

X, м

у, м

S, м

Ha пункт

831

250,25

8511 500,41 2093,992

343°2Г42,18"

5 833 256,57

8 510 900,84

2093,992

343°2Г42,18"

ка этих вычислений подробно рассмотрена в главах 7

табл. 121 даны лишь конечные резуль-

таты: приведенные к центрам знаков

и редуцированные на плоскость в про-

екции Гаусса — Крюгера значения

измеренных направлений и длин сто-

рон. В этой таблице веса измеренных

направлений приняты равными едини-

це (р

=1), а веса измеренных сторон

вычислены по формуле (13.4), в ко-

торой средние квадратические ошибки

длин сторон m

выражены в децимет-

рах, а величина т

принята равной мо-

дулю средней квадратической ошибки

измеренного направления.

Согласно техническому заданию угловые и линейные

пия в нашей сети должны быть исполнены с точностью,

11, то в

РИС. 57

измере-

которая

Таблица 121

Измеренные и приведенные к центрам знаков и на плоскость

горизонтальные направления и длины сторон

Пункт

Направле-

ния

Измеренные направ-

ления N

ifc

Измеренные стороны

, м

Веса измеренных

СТОРОН pfo

1-2 0°00'00,00"

1-3

57 20 32,10

2300,060

32,60

1-4 113 14 06,35

3090,353

23,91

2-5

0 00 00,00

3643,234

19,80

2-3

32 12 22,92

2115,919

35,40

2-4

57 50 15,30 4363,611

16,00

2-1

98 26 12,73

3—1

0 00 00,00

3-2

56 25 37,79

3—5

172 53 39,44

2169,073 34,69

3-4

282 29 53,83

2620,909

35,40

4—1

0 00 00,00

4-2

26 09 54,12

4—3

46 36 17,98

4-5

77 59 46,71

3922,860 18,32

5 5—4

0 00 00,00

5—3

39 00 17,79

5—2

70 19 51,51

•217

Таблица 126 Таблица 127

Предварительное решение треугольников

Треуголь-

Вершина

Углы

на пло-

Предваритель-

Длины сторон

ник

Вершина

скости

но

уравненные

из

решения

тре-

скости

углы

угольников,

56°25'37,79"

+0,10"

37,89"

2093,992

66 13 49,81

+0,10

49,91

2300,055

57 20 32,10

+0,10

32,20

2115,921

179 59

59,70

0,30

—0,30

31 19

33,72

+0,57

34,29 2115,919

3 116 28 01,65

+0,57

2,22

3643,224

2 32 12

22,92

+0,57

23,49

2169,082

179 59

58,29

1,71

— 1,71

1,71

31 23

28,73

—0,31

28,42 2169,073

109 36 14,39

—0,30

14,09

3922,873

39 00 17,79

—0,30

17,49

2620,926

180 00 00,91

—0,91

+0,91

—0,91

55 53

34,25

+0,53

34,78 2620,909

77 30 06,17

+0,53

6,70

3090,370

46 36 17,98

+0,54

18,52

2300,081

2 179 59

58,40

1,60

— 1,60

1,60

26 9 54,12

+0,70

54,82

2093,992

40 35

57,43 +0,70

58,13

3090,298

113 14

06,35

+0,70

7,05

4363,549

179 59

57,90

2,10

—2,10

2,10

133°55'43,96"

—0,07

43,89

4363,611

25 37

52,38

—0,07

52,31

2620,927

4 20 26

23,86

—0,06

23,80 2115,912

180 00

00,20 —0,20

о/

+0,20

—0,20

70 19 51,51

+0,20

51,71

4363,611

51 49

52,59 +0,20

52,79 3643,220

57 50 15,30

+0,20

15,50

3922,872

179 59

59,40

0,60

—0,60

0,60

11,21

п = 7

1/ 11,21 гп"

= у — ^у

0,73- = ' "

•218