Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

От функции F перейдем к ее приращению

/а-Да

б4

= (С

)-(С

) + (С

Заменив поправки в углы поправками в стороны по формулам

(11.22) и учитывая, что поправка (1.2) к исходной стороне 1.2

равна нулю, получим

/ р" р" \

fa = Да^ = созЯ

--щ^со8^(1.5)-

+ cosB

2—ТШ^созЛз) (5.6)

или Да

в4

- /х (1.5) + f

(1.6) + /

(2.5) + /

(4.5) +/

(4.6) (5.6).

Сообразуясь с обозначениями углов на рис. 54 и выбирая необ-

ходимые данные из табл. 96, вычислим значения коэффициентов

весовой функции f

а и напишем

fa = Да

в4

= 4,110 (1.5) — 5,632 (1.6) + 3,844 (2.5) +

+ 5,839 (4.5) — 4,341 (4.6)

—

0,292 (5.6).

Составление и решение нормальных уравнений коррелат

Вычисление поправок в стороны и углы треу-

гольников. Закончив составление условных уравнений и весо-

вой функции, выписывают в табл. 99 коэффициенты этих уравне-

ний, от которых переходят по известным правилам к системе нор-

мальных уравнений коррелат (табл. 100), и решают их (табл. 101).

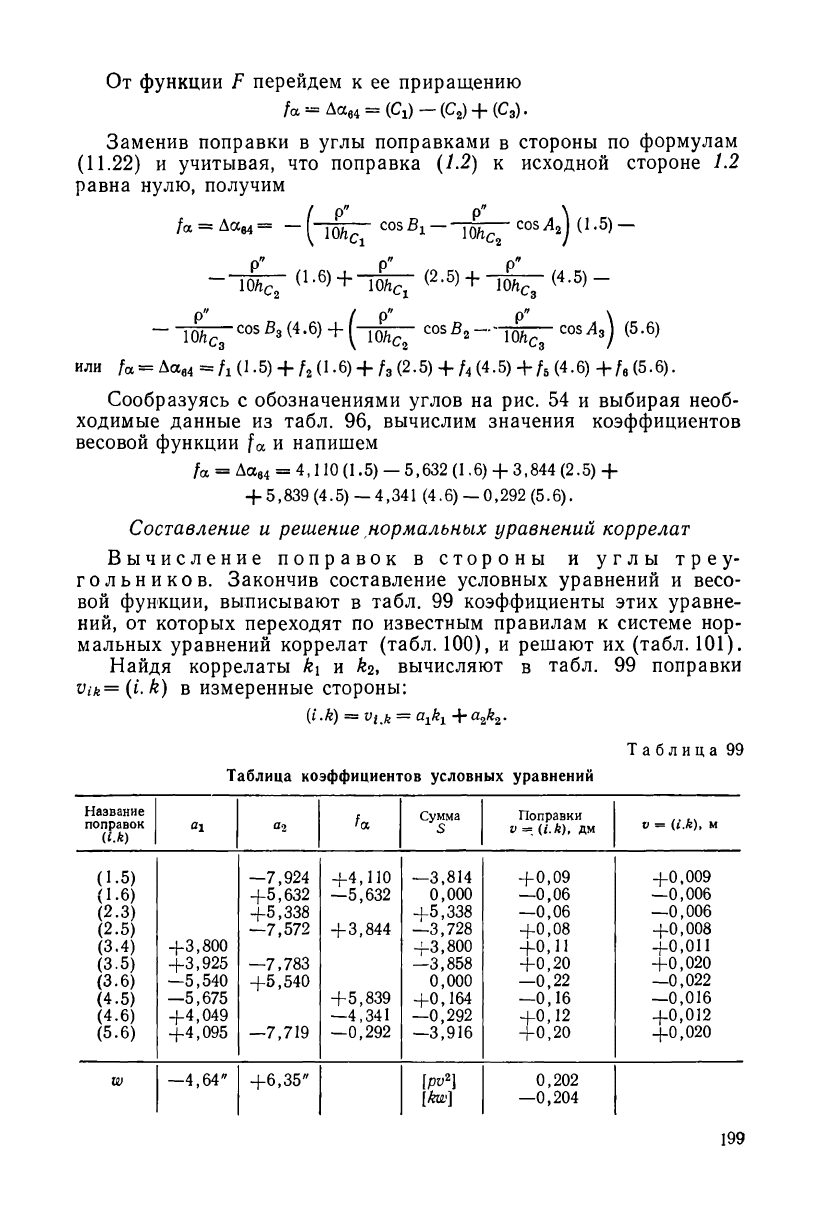
Найдя коррелаты k\ и вычисляют в табл. 99 поправки

Vik=(i.k) в измеренные стороны:

М) = = ЯА +

«2*2-

Таблица 99

Таблица коэффициентов условных уравнений

Название

поправок

(i.k)

а о

Сумма

Поправки

v = (i.k), дм

V = (i.k), м

(1.5) —7,924

+4,110

—3,814

+0,09

+0,009

(1.6)

+5,632

—5,632

0,000

—0,06

—0,006

(2.3) +5,338

—5,632

+5,338

—0,06 —0,006

(2.5)

-7,572

+ 3,844

—3,728

+0,08

+0,008

(3.4)

+3,800

+ 3,844

+3,800

+0,11

+0,011

(3.5) +3,925

—7,783 —3,858

+0,20

+0,020

(3.6)

—5,540

+5,540

0,000

—0,22

—0,022

(4.5)

-5,675

+5,540

+5,839

+0,164

-0,16

—0,016

(4.6)

+4,049

—4,341

—0,292

+0,12

+0,012

(5.6) +4,095 —7,719

—0,292

—3,916 +0,20

+0,020

—4,64" +6,35" [pv*]

Ikw]

0,202

—0,204

199

Таблица

126

Таблица 127

Таблица коэффициентов нормальных уравнений коррелат

Контроль

125,906 —92,849

—51,909 —18,852

—

18,852

125,906

331,188 —91,140

147,199

116,411

—26,638

—26,637

Таблица 101

Решение нормальных уравнений коррелат

S+ w

Контроль

125,906

— 1

—92,849

0,7374

331,188

262,721

—1

1 IP в

—51,909

0,4123

—91,140

—129,418

0,4926

116,411

- = 31,258

—4,64

0,0369

+6,35

2,928

—0,0111

—0,471

—23,492

0,1866

153,549

136,226

—0,5185

—26,638

30,781

0,1866

136,231

—0,5185

30,787

0,0287 —0,0111

Таблица 102

Вычисление уравненных сторон

Сторона

Измерен-

ные сторо-

ны, м

Поправки

из уравни-

вания, м

Уравнен-

ные сто-

роны, м

Сторона

Измерен-

ные сторо-

ны, м

Поправки

из уравни-

вания, м

Уравнен-

ные сто-

роны, м

1.2

1.5

1.6

2.3

2.5

3.4

5365,57

7481,49

7598,57

5407,90

5496,75

+0,009

—0,006

+0,008

+0,011

7611,740

5365,579

7481,484

7598,564

5407,908

5496,761

3.5

3.6

4.5

4.6

5.6

5430,66

7450,68

7615,90

5281,41

5107,83

+0,020

—0,022

—0,016

+0,012

+0,020

5430,680

7450,658

7615,884

5281,422

5107,850

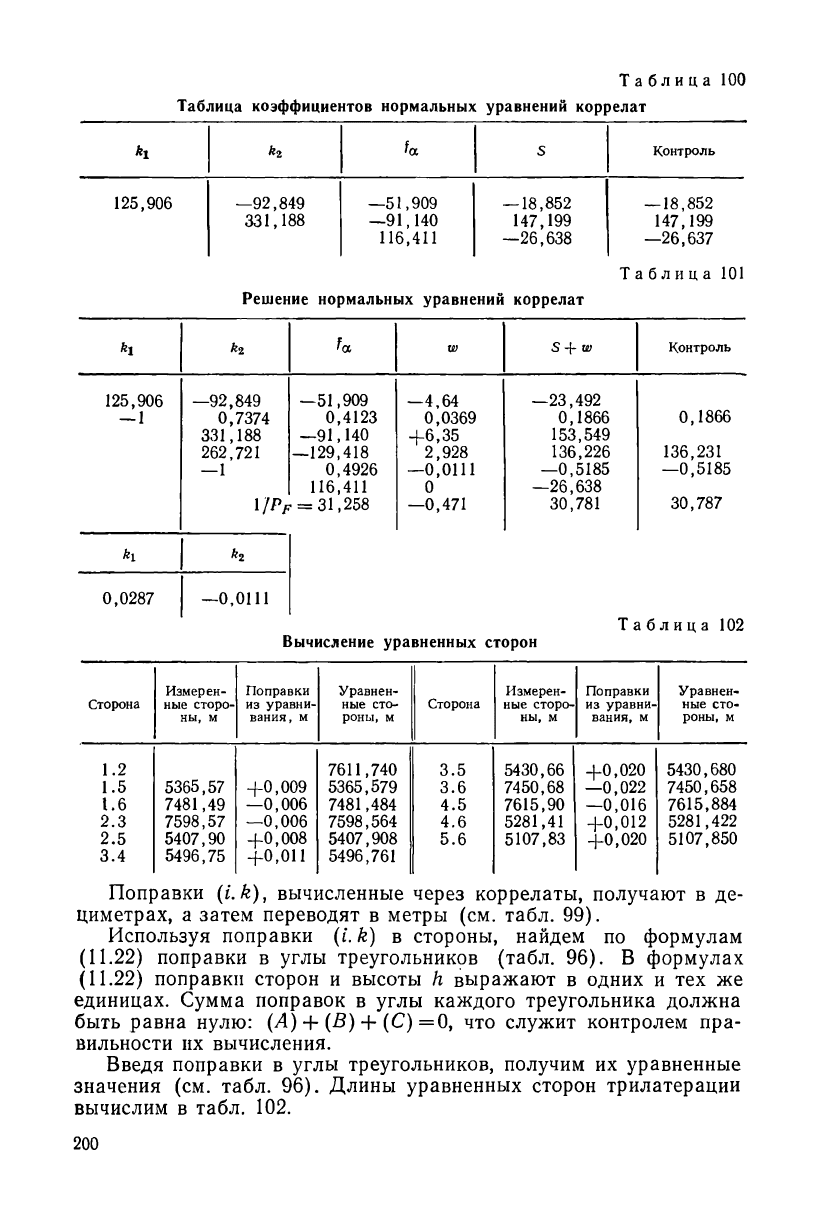
Поправки (L k), вычисленные через коррелаты, получают в де-

циметрах, а затем переводят в метры (см. табл. 99).

Используя поправки (i.k) в стороны, найдем по формулам

(11.22) поправки в углы треугольников (табл. 96). В формулах

(11.22) поправки сторон и высоты h выражают в одних и тех же

единицах. Сумма поправок в углы каждого треугольника должна

быть равна нулю: (А) + (В) + (С) =0, что служит контролем пра-

вильности их вычисления.

Введя поправки в углы треугольников, получим их уравненные

значения (см. табл. 96). Длины уравненных сторон трилатерации

вычислим в табл. 102.

•200

Оценка точности уравненных элементов трилатерации

Вычислив в табл. 99 сумму квадратов поправок в измеренные

стороны, найдем среднюю квадратическую ошибку единицы веса

\i = V(Zpv

)/r = /0,202/2 = 0,32 дм = 0,032 м.

Здесь г — число избыточных измерений, равное числу условных

уравнений (г = 2).

Среднюю квадратическую ошибку дирекционного угла наибо-

лее удаленной стороны 4—6 найдем по формуле

™«

VV^l, = 0,32 /ЗП258 = 1,8".

Обратный вес 1/Ра

вычислен в табл. 101.

Вычисление окончательных координат

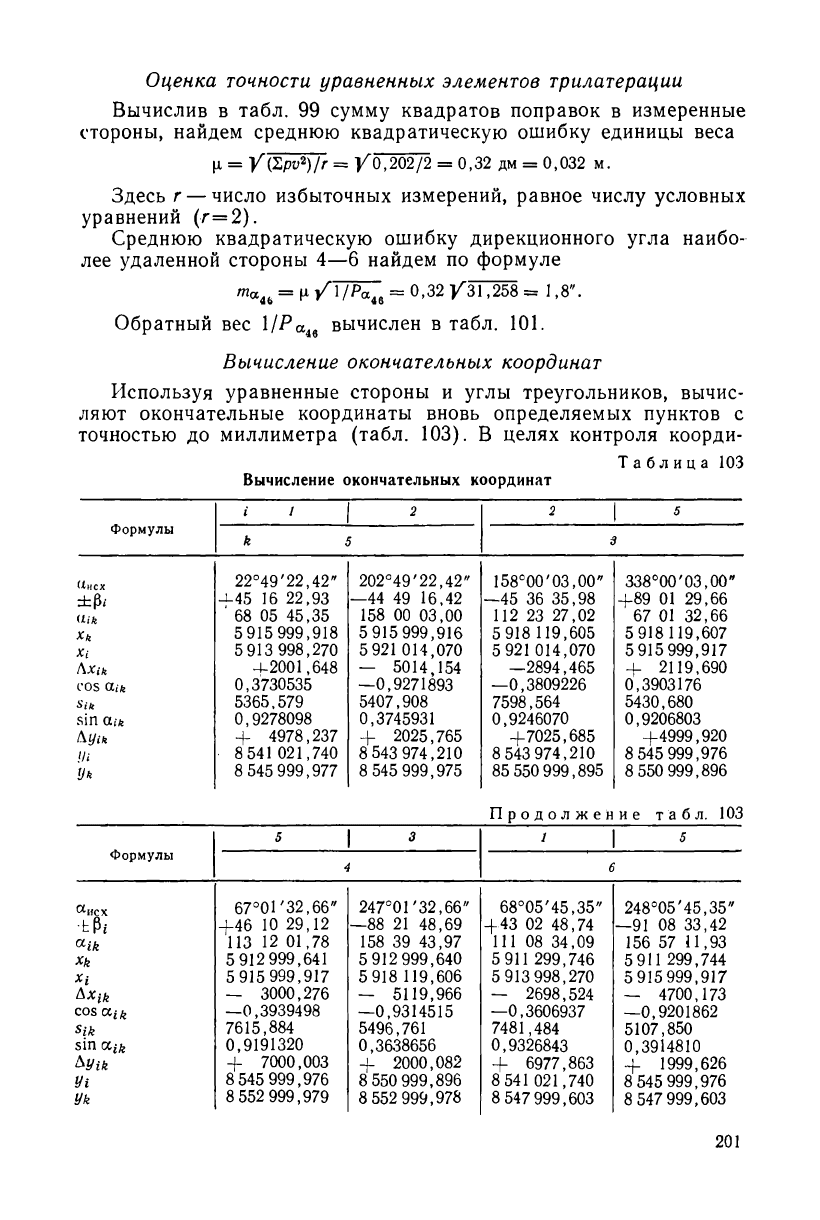
Используя уравненные стороны и углы треугольников, вычис-

ляют окончательные координаты вновь определяемых пунктов с

точностью до миллиметра (табл. 103). В целях контроля коорди-

Таблица 103

Вычисление окончательных координат

Формулы

k 5

Uncx

22°49'22,42"

202°49'22,42"

158°00'03,00"

338°00'03,00"

-L45 16 22,93

—44 49 16,42

—45 36 35,98

+89 01 29,66

(Lift

' 68 05 45,35

158 00 03,00

112 23 27,02

67 01 32,66

5915999,918

5915999,916

5918 119,605 5 918 119,607

5 913 998,270

5 921 014,070

5915999,917

A Xik

-4-2001,648

— 5014,154

—2894,465

+ 2119,690

cos a ik

0,3730535

—0,9271893

—0,3809226 0,3903176

sni

5365,579

5407,908

7598,564

5430,680

sin a ik

0,9278098

0,3745931

0,9246070

0,9206803

Ayik

+ 4978,237 + 2025,765

+7025,685

+4999,920

Ayik

8 541 021,740

8 543 974,210

8 543 974,210 8 545 999,976

8 545 999,977

8 545 999,975 85 550 999,895

8 550 999,896

Продолжение табл. 103

Формулы

1 '

' 1

1 '

Формулы

исх

67°0l'32,66"

247°01'32,66" 68°05'45,35"

248°05'45,35"

+46 10 29,12

—88 21 48,69

+43 02 48,74

—91 08 33,42

113 12 01,78

158 39 43,97

111 08 34,09

156 57 11,93

5912999,641

5 912 999,640

911

299,746

911

299,744

A x

5 915 999,917

5918 119,606

5 913 998,270

5915999,917

A x

— 3000,276

— 5119,966 — 2698,524

— 4700,173

cos

a ik

—0,3939498

—0,9314515

—0,3606937

—0,9201862

Sik

7615,884

5496,761

7481,484

5107,850

sin a ik

0,9191320

0,3638656

0,9326843 0,3914810

Ayik

+ 7000,003

+ 2000,082

+ 6977,863

+ 1999,626

У1

8 545 999,976

8 550 999,896

541

021,740

8 545 999,976

8 552 999,979

8 552 999,978

8 547 999,603

201

наты вычисляют по двум сторонам треугольника. Расхождения в

координатах одного и того же пункта допускают не более трех

единиц последнего знака.

Полученные координаты затем округляют до 0,01 м и выписы-

вают в каталог. Кроме координат в каталоге приводят длины сто-

рон (до 0,01 м) и их дирекционные углы (до сотой доли секунды

дуги), вычисленные из решения обратных геодезических задач.

Глава 12

УРАВНИВАНИЕ ТРИЛАТЕРАЦИИ

ПАРАМЕТРИЧЕСКИМ СПОСОБОМ

§ 63. Общие положения. Список исходных данных

Несвободные сети трилатерации уравнивают обычно парамет-

рическим способом. Последовательность уравнительных вычисле-

ний проследим на примере уравнивания небольшой сети 3 класса,

Таблица 104

Список исходных данных

Номер

На

пункта

X, м

у, м

S, м

пункт

5 944 017,27

8 513 655,31

9 660,75 29° 57'21,17"

5 952 387,44

8 518 479,24 11 647,66

144 26 50,22 3

5 942 911,13

8 525 251,79

11 649,12

275 26 55,40

изображенной на рис. 55. При этом будем полагать, что стороны

в данной сети измерены равноточно, приведены к центрам знаков

и редуцированы на плоскость в проекции Гаусса — Крюгера. Ко-

ординаты исходных пунктов даны в табл. 104, а значения измерен-

ных сторон — в табл. 105.

202

При уравнивании трилатерации параметрическим способом вы-

числяют сначала углы треугольников, приближенные координаты

определяемых пунктов и длины всех сторон сети, соответствующие

этим координатам. Затем составляют уравнения поправок сторон

и соответствующие им нормальные уравнения, из решения которых

находят поправки к приближенным координатам. Используя эти

поправки, вычисляют окончательные координаты пунктов и по-

правки к значениям измеренных сторон. Далее вычисляют урав-

ненные стороны и углы треугольников. Вторично, в целях контро-

ля, вычисляют окончательные координаты через их приращения.

Выполняют оценку точности и составляют каталог координат.

§ 64. Вычисление углов треугольников

и приближенных координат пунктов

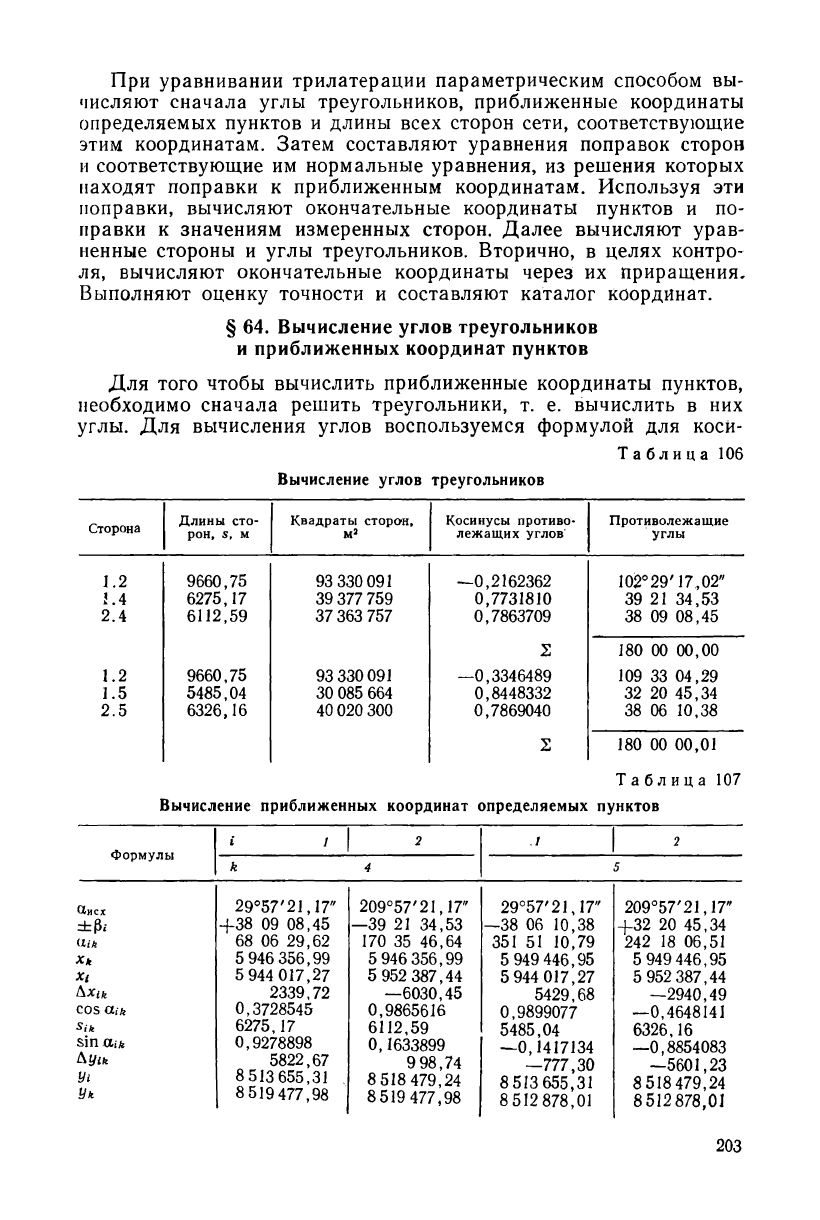
Для того чтобы вычислить приближенные координаты пунктов,

необходимо сначала решить треугольники, т. е. вычислить в них

углы. Для вычисления углов воспользуемся формулой для косй-

Таблица 106

Вычисление углов треугольников

Сторона

Длины сто-

рон, S, м

Квадраты сторо>н,

Косинусы противо-

лежащих углов

Противолежащие

углы

1.2

1.4

2.4

9660,75

6275,17

6112,59

330 091

39 377

759

37 363

757

—0,2162362

0,7731810

0,7863709

102°29'17,02"

39 21 34,53

38 09 08,45

180 00 00,00

Г Г

сл сл to

9660,75

5485,04

6326,16

330

091

085

664

40 020

300

—0,3346489

0,8448332

0,7869040

109 33 04,29

32 20 45,34

38 06 10,38

180 00 00,01

Таблица 107

Вычисление приближенных координат определяемых пунктов

Формулы

i 1

Формулы

(Хисх

llik

kXik

cos a ik

sin

aik

tbyik

Ук

29°57'21,17"

+38 09 08,45

68 06 29,62

5 946 356,99

5 944 017,27

2339,72

0,3728545

6275,17

0,9278898

5822,67

8 513 655,31 .

8 519 477,98

209°57'21,17"

—39 21 34,53

170 35 46,64

5 946 356,99

5 952 387,44

—6030,45

0,9865616

6112,59

0,1633899

9 98,74

8 518 479,24

8 519 477,98

29°57'21,17"

—38 06 10,38

351 51 10,79

5 949 446,95

5 944 017,27

5429,68

0,9899077

5485,04

—0,1417134

—777,30

8513655,31

8 512 878,01

209°57'21,17"

+32 20 45,34

242 18 06,51

5 949 446,95

5 952 387,44

—2940,49

—0,4648141

6326,16

—0,8854083

—5601,23

8 518 479,24

8512 878,01

203

Таблица

126

Таблица 127

Координаты определяемых пунктов

Пункт

Приближенные

Поправки

Окончательные

Пункт

у*. м

6x,

6y,

У, м

5 946 356,99

5 949 446,95

8 519 477,98

8 512 878,01

—0,01

+0,01

+0,03

-0,03

5 946 356,98

5 949 446,96

8519478,01

8 512 877,98

нуса угла треугольника (11.1). В нашей сети для определения ко-

ординат пунктов 4 и 5 достаточно решить два треугольника 124

и 125. Углы вычисляют до 0,01" (табл. 106).

Вычисление приближенных координат определяемых пунктов

дано в табл. 107, причем с контролем по двум сторонам треуголь-

ника. Среднее из двух значений и абсцисс, и ординат каждого

пункта записывают в табл. 108. Последние 4 графы табл. 108

заполняют после решения системы нормальных уравнений.

§ 65. Вычисление длин сторон

по приближенным координатам

Для того чтобы получить свободные члены уравнений поправок

сторон, строго соответствующие приближенным координатам, при-

веденным в табл. 108, необходимо вычислить по этим координатам

длины всех сторон сети. Эти вычисления выполняют с контролем

по формулам:

ik в

уь

Ьу2 _ Дя/cos a

ik = Ay/sin а

**, (12.1)

где

tga°i* = Ar//Ax, (12.2)

А х=х°

-х<>г, Ay = y°k-y°i- (12.3)

Решение обратных геодезических задач по координатам, при-

веденным в табл. 104 и 108, дано в табл. 109. Вычисления длин и

дирекционных углов сторон ведут с семью значащими цифрами.

§ 66. Составление уравнений поправок сторон

Для любой стороны, измеренной от определяемого пункта i до

определяемого пункта k

уравнение поправок записывается в виде

Vik

= — Cikli —dikt\i + Ci

lk + d

Щ +

hk>

(12.4)

где I, r\ — поправки к приближенным координатам пунктов, вы-

раженные в дециметрах, с, d — коэффициенты, I — свободный член

уравнения поправок.

Коэффициенты с

d вычисляют по формулам

— cos

аV = =

= sina

^ =

y°k —y°i

(12.5)

•204

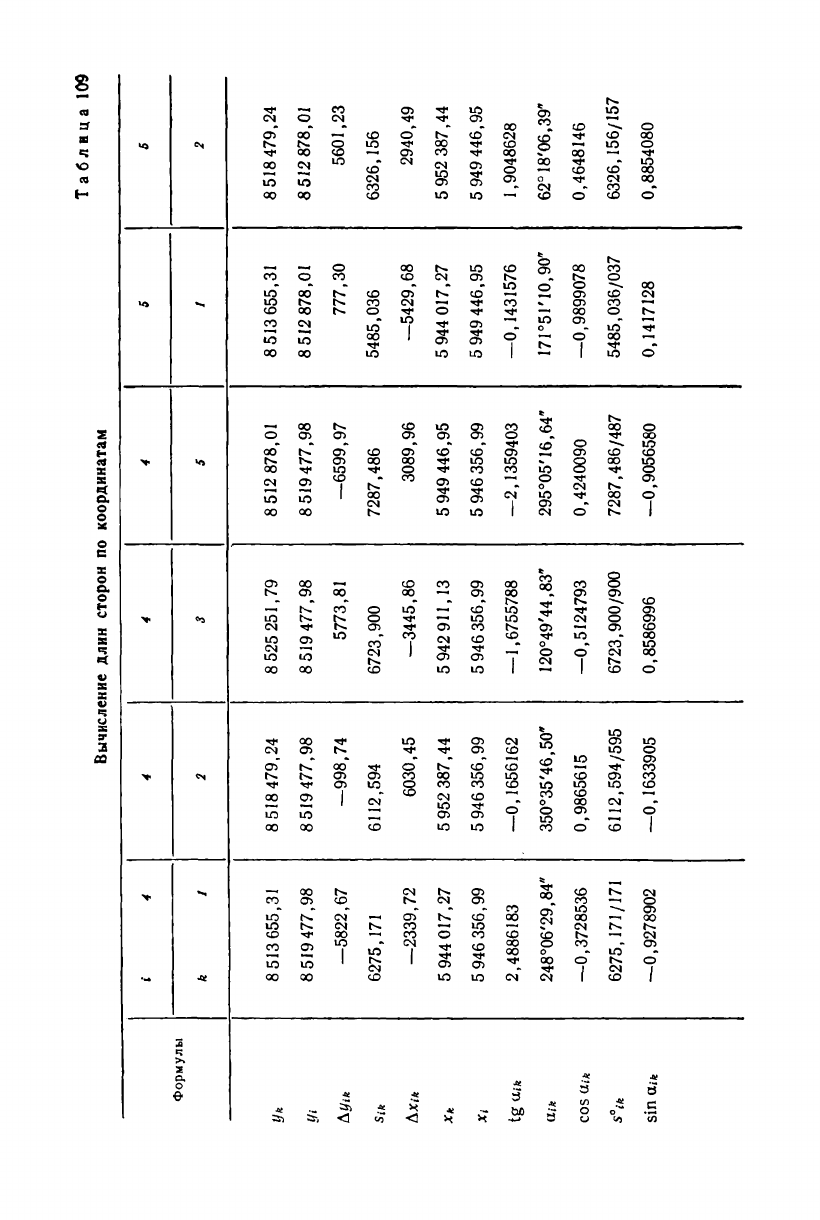
Таблица 109

Вычисление длин сторон по координатам

i 4

Формулы

k /

Ук

8513655,31

8 518 479,24

8 525 251,79

8512 878,01

8 513 655,31

8 518 479,24

У'1

8 519 477,98

8 519477,98

8512 878,01

8 512 878,01

Д yik

—5822,67

—998,74

5773,81

—6599,97

777,30

5601,23

Sik

6275,171

6112,594 6723,900

7287,486

5485,036

6326,156

Д Xik

—2339,72

6030,45

—3445,86

3089,96

—5429,68

2940,49

5 944 017,27

5 952 387,44

5942911,13

5 949 446,95

5 944 017,27

5 952 387,44

5 946 356,99

5 949 446,95 5 949 446,95

tg Шк

2,4886183

—0,1656162

—1,6755788 —2,1359403

—0,1431576

1,9048628

Ilik

248°06'29,84"

350° 35'46,50"

120°49

44,83"

295°05'16,64"

17Г5Г10,90"

бгЧв'Об^"

cos aik

—0,3728536

0,9865615

—0,5124793

0,4240090

—0,9899078

0,4648146

s ik

6275,171/171

6112,594/595

6723,900/900

7287,486/487

5485,036/037

6326,156/157

sin a ik

—0,9278902

—0,1633905

0,8586996

—0,9056580

0,1417128

0,8854080

Свободный член находят как разность двух значений длины

стороны: вычисленной по приближенным координатам и по-

лученной из измерений s'ik (на плоскости); выражают его в деци-

метрах:

^10A

, (12.6)

где разность А^ вычисляется в метрах:

= - s'ik = VWk-xOtf-tWk-yOtf -s'

. (12.7)

Если сторона измерена от исходного пункта i

(Ei

ri*

= 0) Д°

определяемого пункта k, то уравнение поправок запишется в виде

Vik = c

U+dik

+ hk- (12.8)

Если пункт £ является определяемым, а пункт ft-исходным

(5*

т)*

= °)» тогда

Щк = —CikU

—

dikm + lik- (12.9)

Если расстояние измерено между исходными пунктами (|==ri =

= 0), то уравнение поправок запишется в виде

vtk = hk- (12.10)

Применительно к вычислениям на ЭВМ уравнениям поправок

сторон (12.4) целесообразно придать вид

» y°k-y°i ,

Е|

~ +

^V/

Чк

+ hk, (12.11)

где s°ik вычисляют по формуле (12.1), a Uk — по формуле (12.6);

— приближенные координаты концов стороны.

Для всех измеренных сторон нашей сети вычислим коэффици-

енты и свободные члены уравнений поправок (табл. 110).

Таблица 110

Вычисление коэффициентов и свободных членов уравнений

поправок сторон

Сторона

ik~

cos a

°ik

-slna^

>°ik'

*'ik>

4.1

—0,373 —0,928 6275,171 6275,170

0,001

0,01

4.2

0,987

—0,163 6112,594 6112,590 0,004

0,04

4.3

—0,512 0,859 6723,900

6723,850

0,050

0,50

4.5

0,424 —0,906

7287,486

7287,570

—0,084

—0,84

5.1

—0,990

0,142

5485,036

5485,040

—0,004

—0,04

5.2

0,465 0,885 6326,156

6326,160

—0,004

—0,04

При составлении табл. 110 значения cos a

/*, sin а

/* и s

,* вы-

писывают из табл. 109 с тремя десятичными знаками после запя-

той; измеренные расстояния s'i

берут из табл. 105. Свободные

члены Uk вычисляют до 0,01 дм.

206

Таблица

126

Таблица

127

Таблица коэффициентов уравнений поправок

Поправки

к стороне

<»".

к)

Коэффициенты при поправках

'i*

дм

Сумма

Вес

Pik

Поправки

«. *).

дм

Поправки

к стороне

<»".

к)

Т15

'i*

дм

Сумма

Вес

Pik

Поправки

«. *).

дм

(4.1)

(4.2)

(4.3)

(4.5)

(5.1)

(5-2)

0,373

—0,987

0,512

—0,424

0,928

0,163

—0,859

0,906 0,424

0,990

—0,465

—0,906

—0,142

—0,885

0,01

0,04

0,50

—0,84

—0,04

1,311

—0,784

0,153

—0,840

0,808

— 1,390

0,25

0,24

0,14

-0,16

0,14

0,15

[ри

] = 0,213

В соответствии с выражениями (12.4) и (12.8), (12.9) ис уче-

том данных, приведенных в табл. 110, составим табл. 111 коэффи-

циентов и свободных членов уравнений 'поправок. Число уравнений

равно числу измеренных сторон в сети трилатерации, к которым

определяются поправки из уравнивания. Для базисных сторон, ко-

торые принимаются за исходные стороны, поправки не определя-

ются (они равны нулю).

Последняя графа табл. 111 заполняется после определения по-

правок координат (£, г]) из решения системы нормальных уравне-

ний.

§ 67. Составление весовых функций

Для вычисления средних квадратических ошибок определения

уравненных значений длины и дирекционного угла любой сторо-

ны, например стороны 4—5, расположенной в слабом месте сети,

необходимо составить соответствующие им весовые функции, ко-

торые, как и ранее, запишутся в виде уравнений поправок сторон

и поправок направлений, но без свободных членов и поправок

ориентирования на станциях, т. е. в виде

= As

= — с

— d

+ C

l б + d

;

fa = Да

= —«45^4 —

4Ь*\4 + Я45?5 + ^45^6

где коэффициенты а, b, с, d вычисляют по формулам (10.6) и

(12.5), используя приближенные координаты пунктов. Вычисления

этих коэффициентов даны в табл. 112.

Линейный вид весовых функций:

= —0,424£

+ 0,906т]

+ 0,424£

- 0,106т|

;

fa = —2,563|

- 1,

200т]4

+ 2,563£

+ 1,200т]

Коэффициенты весовых функций записывают в табл. 113 (гра-

фы f

н f

) в строках тех нормальных уравнений, при квадратич-

ных коэффициентах которых стоят соответствующие им поправ-

ки £ и Г).

•207

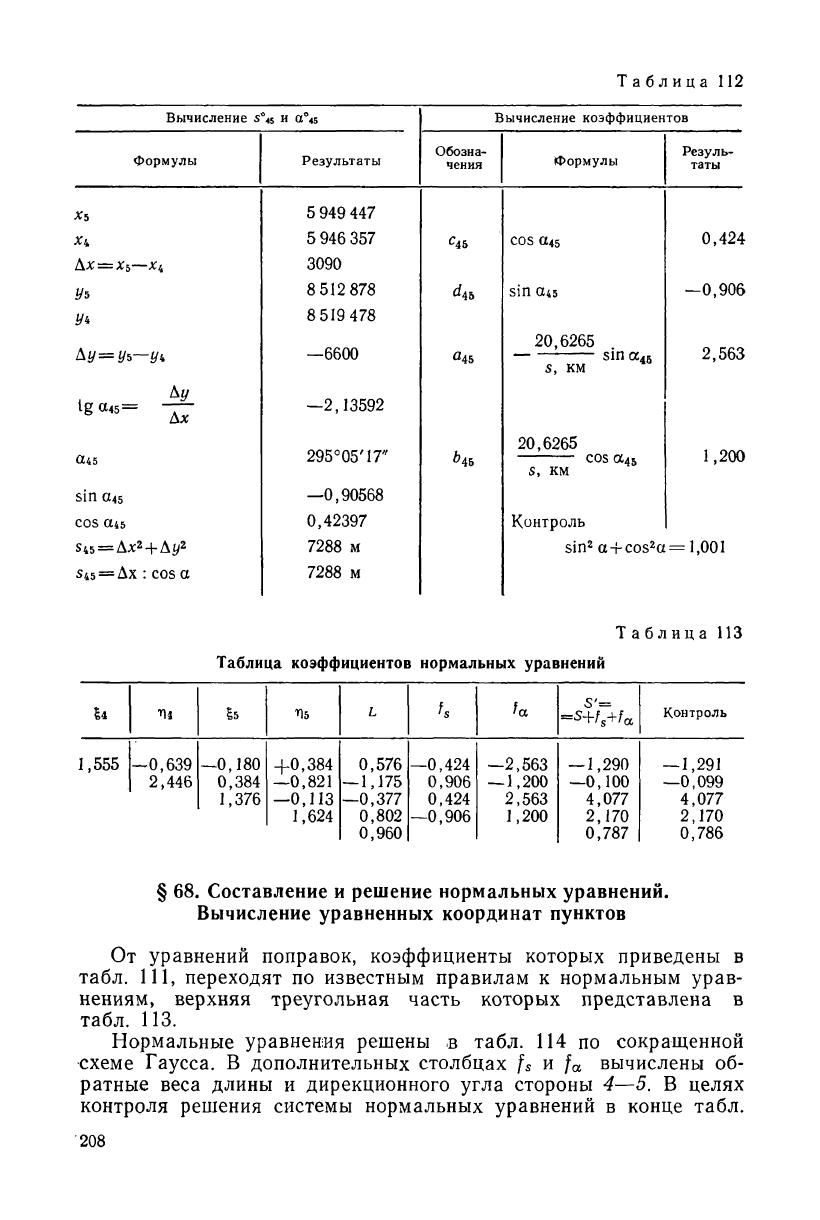
Таблица

126

Таблица

127

Вычисление 5

°4S И

a°45

Вычисление коэффициентов

Формулы Результаты

Обозна-

чения

Формулы

Резуль-

таты

5 949 447

5 946 357

^45

cos a

0,424

3090

Уь

8 512 878

^45

Sin (*45

—0,906

Уь

8 519 478

ку = уь—уь

—6600 a

20,6265

— sin a

S, KM

2,563

lg(X45=

—2,13592

Й45

295°05'17"

20,6265

cos a

S, KM

1,200

sin a

—0,90568

COS Ct

0,42397 Контроль

5 = Ax

+ A^

7288 м

sin

a + cos

= 1,001

= AX

cos a

7288 м

Таблица 113

Таблица коэффициентов нормальных уравнений

"Па

LB Л5

Контроль

1,555

—0,639

2,446

—0,180

0,384

1,376

+0,384

—0,821

—0,113

1,624

0,576

— 1,175

—0,377

0,802

0,960

—0,424

0,906

0,424

—0,906

—2,563

— 1,200

2,563

1,200

— 1,290

—0,100

4,077

2,170

0,787

— 1,291

—0,099

4,077

2,170

0,786

§ 68. Составление и решение нормальных уравнений.

Вычисление уравненных координат пунктов

От уравнений поправок, коэффициенты которых приведены в

табл. 111, переходят по известным правилам к нормальным урав-

нениям, верхняя треугольная часть которых представлена в

табл. 113.

Нормальные уравнения решены в табл. 114 по сокращенной

схеме Гаусса. В дополнительных столбцах f

и f

вычислены об-

ратные веса длины и дирекционного угла стороны 4—5. В целях

контроля решения системы нормальных уравнений в конце табл.

•208