Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

установлена для этих измерений в геодезических сетях 2 класса,

то есть со средними квадратическими ошибками, не превышающи-

ми т= 1" и m

/s= 1/300 000 соответственно.

Прежде чем приступить к уравниванию сети, надо проверить,

удовлетворяют ли результаты угловых и линейных измерений ус-

тановленным для них техническим допускам. С этой целью вычис-

лим фактические величины средних квадратических ошибок изме-

ренных углов и сторон, а также свободные члены условий фигур и

полюсных. Полученные результаты сравним с установленными для

них допусками.

Сначала рассмотрим линейно-угловую сеть как сеть триангуля-

ции. Начнем с вычисления невязок всех треугольников, которые

имеются в сети. Вычисленные в табл. 122 невязки не превышают

установленного для триангуляции 2 класса допуска

а/'доп — 2,Ьт" /3-2,5.1" /3*= 4\ (13.10)

Средняя квадратическая ошибка угла, вычисленная в табл. 122

по невязкам треугольников, также получилась меньше установлен-

ной величины (т = 0,73

при допуске т=

Теперь вычислим свободные члены полюсных условных уравне-

ний и сравним их величины с установленными для них допусками.

Число полюсных условий в нашей сети определим по формуле

с = р —2п + з, (13.11)

где р — число всех сторон, п — число всех пунктов в сети.

При р = 9 и п =

получим

Возникают эти условия в гео-

дезическом четырехугольнике и центральной системе.

Допустимые значения свободных членов полюсных условий вы-

числяют по формуле

tt>

AOn

= 2,5m''/Sctg2 р, (13.12)

где т" — заданная величина средней квадратической ошибки из-

мерения углов, р — связующие углы треугольников.

Вычисление свободного члена полюсного условия

геодезического четырехугольника

а) Чертеж фигуры (рис. 58).

б) Название полюса: пункт 3

в) Запись условия

= 1.

ИЛИ

sin

(14

—

12)sin

(6—5) sin (2 — 1)

sin

(<3 — 2)

sin

(14 —

IS) sin

—

= 1.

РИС. 53

219

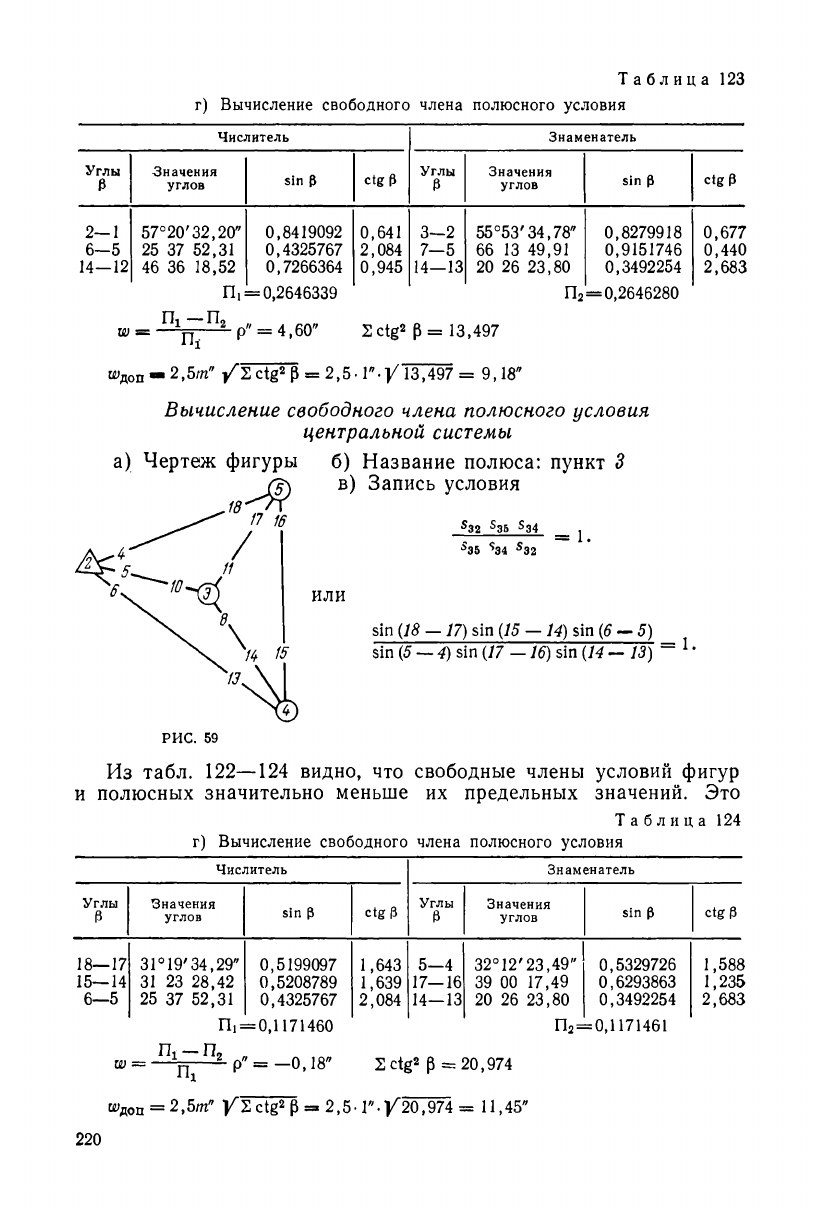
Таблица 123

г) Вычисление свободного члена полюсного условия

Числитель

Знаменатель

Углы

Значения

углов

sin 3

Ctg 0

Углы

Значения

углов

sin 3

ctg 0

2—1

6-5

14-12

57°20'32,20"

25 37 52,31

46 36 18,52

0,8419092

0,4325767

0,7266364

0,641

2,084

0,945

3-2

7-5

14—13

55°53'34,78"

66 13 49,91

20 26 23,80

0,8279918

0,9151746

0,3492254

0,677

0,440

2,683

W :

П!

= 0,2646339

—0,2646280

2ctg

р = 13,497

ОП-2,5/л" /2 ctg

р = 2,5-Г У13,497= 9,18"

Вычисление свободного члена полюсного условия

центральной системы

а) Чертеж фигуры б) Название полюса: пункт 3

в) Запись условия

ИЛИ

sin

(18

—17) sin

(15

—

14)

sin

— 5)

sin

—

sin

(17

—16) sin

(14

— 13)

= 1.

РИС. 59

Из табл. 122—124 видно, что свободные члены условий фигур

и полюсных значительно меньше их предельных значений. Это

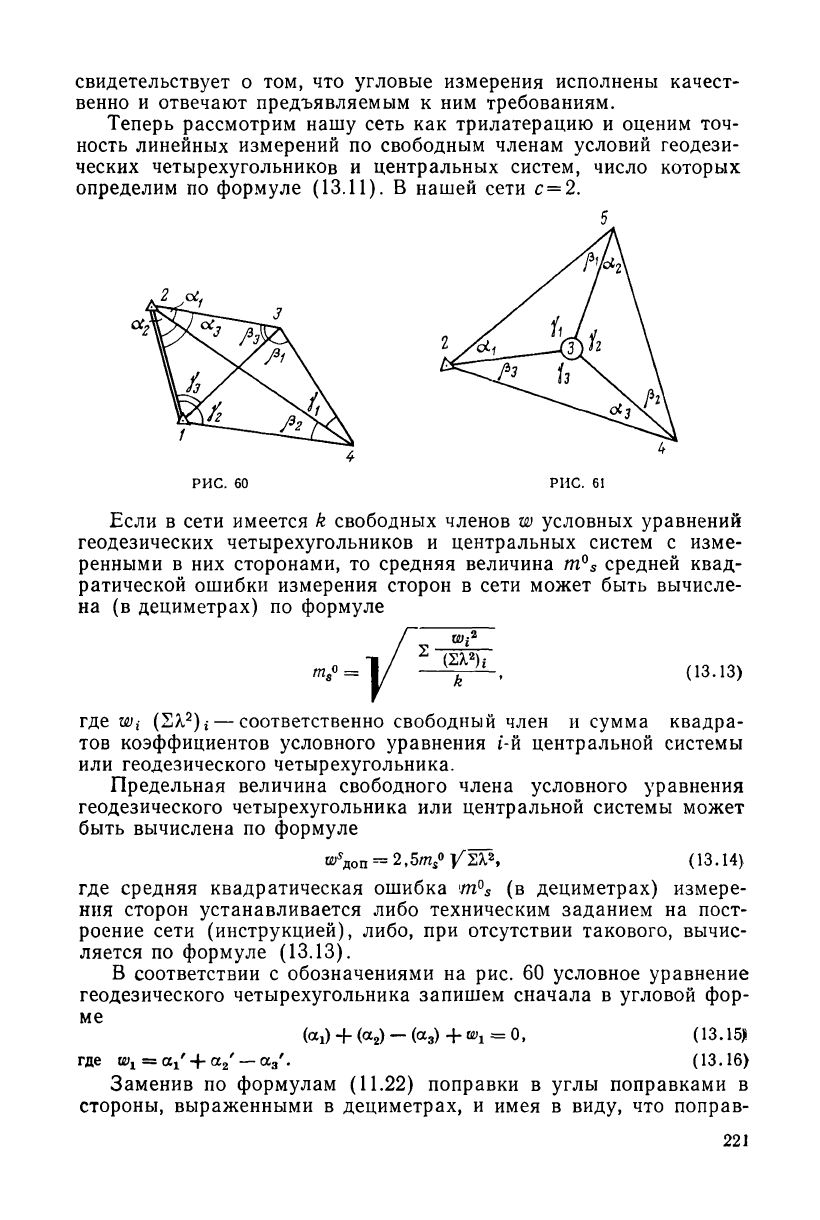
Таблица 124

г) Вычисление свободного члена полюсного условия

Числитель Знаменатель

Углы

Значения

углов

sin 0

ctgfl

Углы

Значения

углов

sin 0 Ctg 0

18—17

15—14

6—5

31°19'34,29"

31 23 28,42

25 37 52,31

0,5199097

0,5208789

0,4325767

1,643

1,639

2,084

5-4

17—16

14-13

32°12'23,49"

39 00 17,49

20 26 23,80

0,5329726

0,6293863

0,3492254

1,588

1,235

2,683

П1

= 0,1171460

= 0,1171461

w =

П1

р" = —0,18" 2 ctg

р 20,974

о>доп = 2,5т" /2 ctg

Р = 2,5»

1".

/2М74 = 11,45"

220

свидетельствует о том, что угловые измерения исполнены качест-

венно и отвечают предъявляемым к ним требованиям.

Теперь рассмотрим нашу сеть как трилатерацию и оценим точ-

ность линейных измерений по свободным членам условий геодези-

ческих четырехугольников и центральных систем, число которых

определим по формуле (13.11). В нашей сети

= 2.

РИС. 60 РИС. 61

Если в сети имеется k свободных членов w условных уравнений

геодезических четырехугольников и центральных систем с изме-

ренными в них сторонами, то средняя величина m°

средней квад-

ратической ошибки измерения сторон в сети может быть вычисле-

на (в дециметрах) по формуле

-,/

(П»),

V "

(13.13)

где Wi (EX

)* — соответственно свободный член и сумма квадра-

тов коэффициентов условного уравнения i-й центральной системы

или геодезического четырехугольника.

Предельная величина свободного члена условного уравнения

геодезического четырехугольника или центральной системы может

быть вычислена по формуле

^доп = 2,5/n

° УШ, (13.14)

где средняя квадратическая ошибка m°

(в дециметрах) измере-

ния сторон устанавливается либо техническим заданием на пост-

роение сети (инструкцией), либо, при отсутствии такового, вычис-

ляется по формуле (13.13).

В соответствии с обозначениями на рис. 60 условное уравнение

геодезического четырехугольника запишем сначала в угловой фор-

ме

(<*i) + (<*

) - (<*з) = (13.15)

где w

= a

' + a

'— а

'. (13.16)

Заменив по формулам (11.22) поправки в углы поправками в

стороны, выраженными в дециметрах, и имея в виду, что поправ-

221

ка к исходной стороне s 12 должна быть равна нулю ,[(1.2) =0], за-

пишем условное уравнение (13.15) в окончательном виде

Vi (3.4) + v

(1.4) + v, (1.3) + v

(2.3) + v

(2.4) + w

= 0, (13.17)

где при высотах h

, заданных в метрах, принято:

ЮЛп

1 О/га

Ю/Za,

Ю/lQ

cos Y/+-

10 h

(13.18)

Условное уравнение центральной системы (рис. 61) напишем

сначала в угловой форме

(Yi) + (Yi) + M + w. = °, (13.19)

где

= 7i' + Y2'+Y3'~ 360°. (13.20)

После замены поправок в углы поправками в стороны, выра-

женными в дециметрах, условное уравнение (13.19) запишем в

окончательном виде:

V (2.5) + V (4.5) +

Я,®

(2-

) + (2-

) + <

) +

з (3.4) + = 0, (13.21)

где при высотах h

заданных в метрах, принято:

Р" _ Р" .

ЧЛ

= -(

10h

•

р'

т-

io*

cos

^' + l0h^

cos

Р»

ЮЛ-

cos

' +'

ЮЛ

*з

cos a

' +

10/z

10hy

cos Px^;

cos p

').

10/i-

(13.22)

Углы a

, p' и у' вычисляют по измеренным сторонам треуголь-

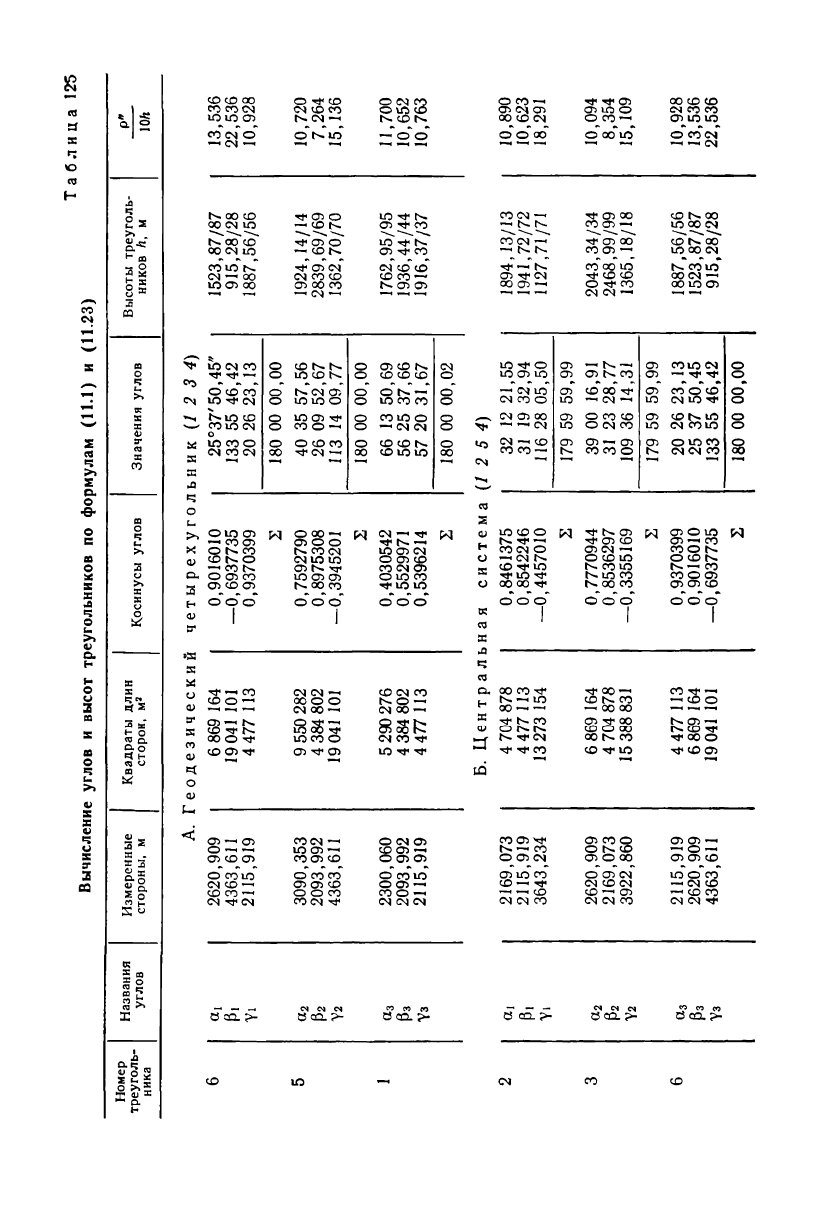
ников (табл. 125). Коэффициенты (13.18), (13.22) и свободные

члены условных уравнений геодезического четырехугольника и

центральной системы вычислены в табл. 126 и 127.

Средняя величина средней квадратической ошибки m°

измере-

ния сторон, вычисленная в дециметрах по формуле (13.13), оказа-

лась равной

Т2~

2,68

6,23

1184,434 + 4258,359

i 0,09 дм = 0,009 м*

222

Таблица

109

Вычисление углов и высот треугольников по формулам (11.1) и (11.23)

Номер

треуголь-

ника

Названия

углов

Измеренные

стороны, м

Квадраты длин

сторон, м

Косинусы углов Значения углов

Высоты треуголь-

ников h, м

Р"

10 h

А. Геодезический

четырехугольник (1 2 3 4)

<*1

Р.

2620,909

4363,611

2115,919

6 869 164

19041 101

477 113

0,9016010

—0,6937735

0,9370399

25°37'50,45"

133 55 46,42

20 26 23,13

1523,87/87

915,28/28

1887,56/56

13,536

22,536

10,928

180 00 00,00

«2

Р2

3090,353

2093,992

4363,611

550

282

4 384 802

19 041

101

0,7592790

0,8975308

—0,3945201

40 35 57,56

26 09 52,67

ИЗ 14 09,77

1924,14/14

2839,69/69

1362,70/70

10,720

7,264

15,136

180 00 00,00

Рз

2300,060

2093,992

2115,919

5 290276

4 384

802

4 477 113

0,4030542

0,5529971

0,5396214

66 13 50,69

56 25 37,66

57 20 31,67

1762,95/95

1936,44/44

1916,37/37

11,700

10,652

10,763

180 00 00,02

Б. Центральная система

(1 2 5 4)

Р.

2169,073

2115,919

3643,234

4 704 878

4 477 113

13 273

154

0,8461375

0,8542246

—0,4457010

32 12 21,55

31 19 32,94

116 28 05,50

1894,13/13

1941,72/72

1127,71/71

10,890

10,623

18,291

179 59 59,99

Р2

2620,909

2169,073

3922,860

869

164

4 704 878

15 388

831

0,7770944

0,8536297

—0,3355169

39 00 16,91

31 23 28,77

109 36 14,31

2043,34/34

2468,99/99

1365,18/18

10,094

8,354

15,109

179 59 59,99

Рз

2115,919

2620,909

4363,611

4 477 113

869

164

19 041

101

0,9370399

0,9016010

—0,6937735

20 26 23,13

25 37 50,45

133 55 46,42

1887,56/56

1523,87/87

915,28/28

10,928

13,536

22,536

180 00 00,00

Таблица 126

Вычисление коэффициентов

и свободного члена

условного уравнения

геодезического четырехугольника

Поп-

равка

сто-

роны

Коэффи-

циенты

Углы

Значения

углов

(3.4)

{1.4)

13,536

10,720

25°37'50,45"

40 35 57,56

(1.3)

(2.3)

—11,700

15,864

66 13 48,01

66 13 50,69

(2.4)

—22,310

| —2,68"

2= 1184,434

пу

оп = 2,5т/ =

= 2,5-0,09 У 1184,434 а 7,74*

Таблица 127

Вычисление коэффициентов

и свободного члена

условного уравнения

центральной системы

Поп-

равка

сто-

роны

Коэффици-

енты к

Углы

Значения

углов

(2.5)

(4.5)

(2.4)

18,291

15,109

22,536

Уз

116°28'05,50"

109 36 14,31

133 55 46,42

(2.3)

(3.5)

—35,802

—27,360

""360°

360 00 06,23

(3.4)

—34,019

щ 1

+6,23

2^ = 4258,359

= 2,5 0,091^4258,359= 14,68?

При средней величине длин сторон сети s

=3028 м это приве-

дет к относительной ошибке порядка m

: s

: 336

ООО,

что

практически совпадает с установленной для данной сети величи-

ной относительной ошибки измерения сторон 1 :300 ООО.

Вычисленные значения w

и m°

оказались меньше их допу-

стимых величин, что свидетельствует о соответствии точности ли-

нейных измерений заданным требованиям. Теперь, когда установ-

лено, что угловые и линейные измерения исполнены качественно,

можно приступить к следующему этапу уравнительных вычисле-

ний.

§ 73. Вычисление приближенных координат

определяемых пунктов.

Решение обратных геодезических задач

Для составления уравнения поправок направлений и уравнений

поправок сторон необходимо получить приближенные координаты

определяемых пунктов и соответствующие им значения дирекцион-

ных углов и длин всех сторон сети. Приближенные координаты

пунктов вычисляют до 0,001 м (см. табл. 128), взяв из табл. 122

необходимые углы и длины сторон треугольников. Среднее из двух

значений координат, получаемых по двум сторонам треугольника,

записывают в табл. 129. Последние 4 графы этой таблицы запол-

няют после решения системы нормальных уравнений, из которой

находят поправки координат.

Для вычисления свободных членов уравнений поправок направ-

лений и уравнений поправок сторон необходимо найти дирекцион-

•224

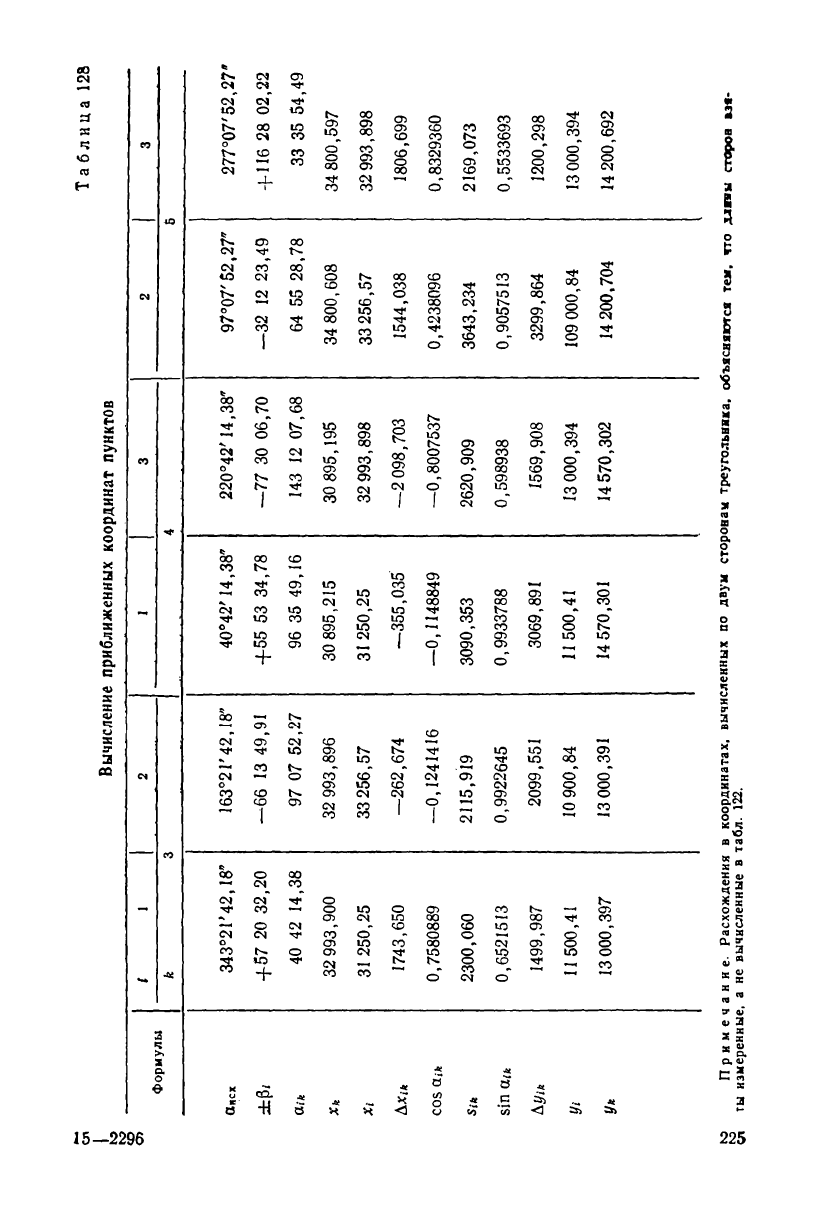
сл Таблица 128

^ Вычисление приближенных координат пунктов

Формулы

k 3

(Хисх

343°2Г42,18" 163°2Г42,18"

40°42' 14,38"

220°42'14,38"

97°07' 52,27"

277°07'52,27

+57 20 32,20

—66 13 49,91

+55 53 34,78

—77 30 06,70 —32 12 23,49

116

28 02,22

CLik

40 42 14,38

97 07 52,27

96 35 49,16

143 12 07,68

64 55 28,78

33 35 54,49

32 993,900

32 993,896 30 895,215

30 895,195

34 800,608

34 800,597

31 250,25

33 256,57

31 250,25 32 993,898

33 256,57

32 993,898

Axik

1743,650

—262,674

—355,035

-2 098,703

1544,038

1806,699

cos a ik

0,7580889

—0,1241416

—0,1148849

—0,8007537

0,4238096

0,8329360

sik

2300,060

2115,919

3090,353

2620,909

3643,234

2169,073

sin a ik

0,6521513

0,9922645

0,9933788

0,598938

0,9057513

0,5533693

A yik

1499,987

2099,551

3069,891

1569,908

3299,864

1200,298

11500,41

10 900,84

11 500,41

000,394

109 000,84

13000,394

Уk

000,397

000,391

570,301

14570,302

200,704

14 200,692

Примечание, расхождения в координатах, вычисленных по двум сторонам треугольника, объясняются те*, тго ддпы сторов

Сл ты измеренные, а не вычисленные в табл. 122.

Таблица

126

Таблица

127

Пункт

Приближенные координаты

Поправки

иэ

уравнивания

Окончательные координаты

Пункт

у°.

м м х,

у,

832

993,898

830

895,205

834

800,602

513

000,394

514

570,302

514

200,698

0,004

—0,002

0,006

0,003

0,002

—0,007

831

250,250

833

256,570

832

993,902

830

895,203

834

800,608

511

500,410

510

900,840

513

000,397

514

570,304

514

200,691

Таблица

130

Пункт

Направления

Дирекционные углы Длины сторон

S°-

1—2

343°2Г42,18"

2093,992

1—3 40

42 14,28

2300,057

1—4 96

49,82 3090,355

2-5 64

28,92 3643,226

2—3 97

52,09 2115,921

2—4 122

43,26 4363,598

2—1

163

21 42,18

2093,992

3-1

220

42 14,28

2300,057

3—2 277

52,09 2115,92]

3—5

54,67

2169,080

3—4

143

07,24

2620,901

4-1

276

49,82

3090,355

4-2

302

43,26

4363,598

4—3

323

07,24

2620,901

4-5

354

35 37,21

3922,848

5 5—4

174

35 37,21

3922,848

5—3

213

54,67

2169,080

5—2

244

28,92 3643,226

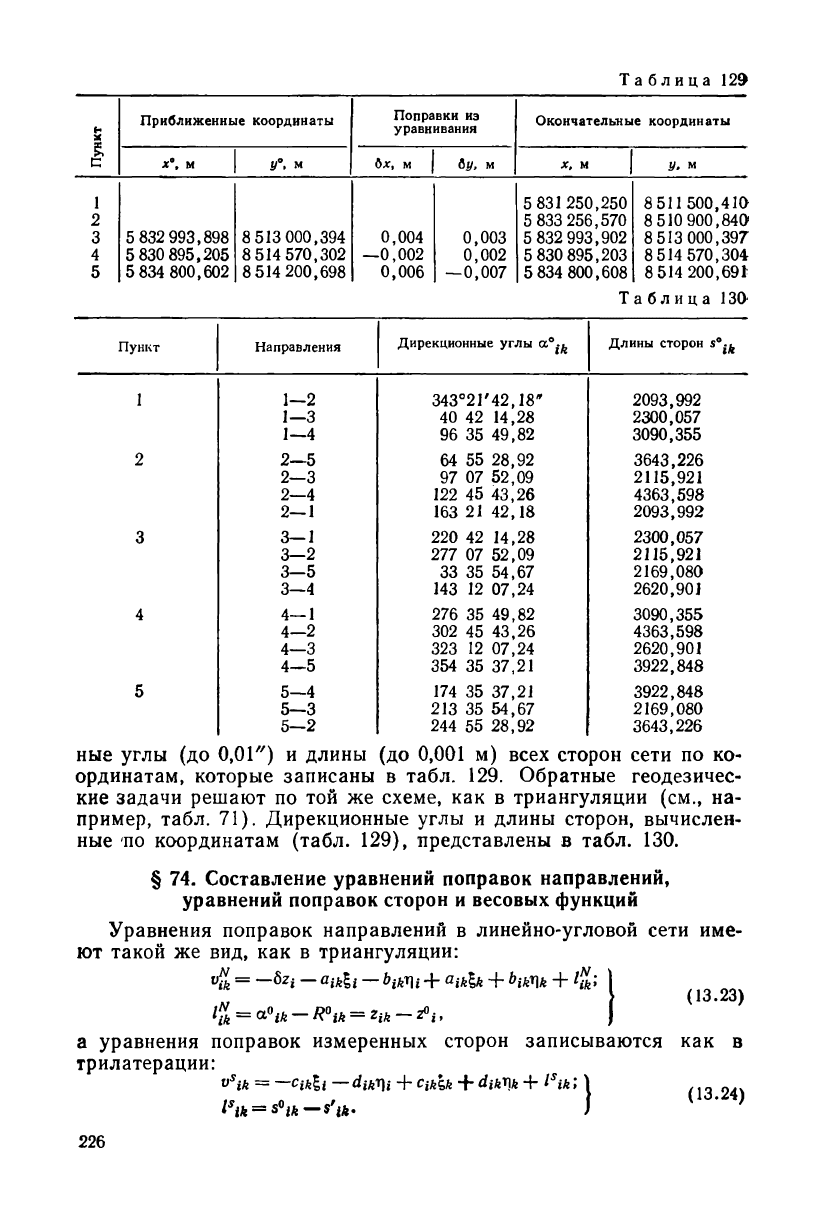
ные углы

(до

0,01")

длины

(до 0,001 м)

всех сторон сети

по ко-

ординатам, которые записаны

табл.

129.

Обратные геодезичес-

кие задачи решают

по той же

схеме,

как в

триангуляции

(см., на-

пример, табл.

71).

Дирекционные углы

длины сторон, вычислен-

ные

'по

координатам (табл.

129),

представлены

табл.

130.

74.

Составление уравнений поправок направлений,

уравнений поправок сторон

весовых функций

Уравнения поправок направлений

линейно-угловой сети

име-

ют такой

же вид, как в

триангуляции:

—

lklt —

bik4i

aiklk

a уравнения поправок измеренных сторон записываются

как в

трилатерации:

—Cikli—

dikr)i

Cikc

dikr\k

ik'»

\ ,

(13.23)

•226

Таблица

109

Вычисление коэффициентов и свободных членов уравнений поправок направлений

Пункт

Нап-

равле-

ние

Измеренные

'направления

Дирекционные

углы

Ориентирую-

щие углы

Приближенно

ориентирован-

ные направления

Свобод-

ные

члены

*°ik> ™

>ik

Вес

Pik

1-2

1-3

1-4

OWOt^OO"

57 20 32,10

113 14 06,35

343

21'42,18"

40 42 14,28

96 35 49,82

343°21'42,18"

343 21 42,18

343 21 43,47

343°2Г42,6Г

40 42 14,71

96 35 48,96

—0,43"

—0,43

+0,86

2,09

2,30

3,09

+2,83

—5,85

—6,63

+9,46

+6,80

—0,77

343 21 42,61

0,00

2—5

2-3

2-4

2-1

0 00 00,00

32 12 22,92

57 50 15,30

98 26 12,73

64 55 28,92

97 07 52,09

122 45 43,26

163 21 42,18

64 55 28,92

64 55 29,17

64 55 27,96

64 55 29,45

64 55 28,88

97 07 51,80

122 45 44,18

163 21 41,61

+0,04

+0,29

—0,92

+0,57

3,64

2,12

4,36

2,09

—5,13

—9,66

—3,98

—2,83

+2,40

— 1,21

—2,56

—9,46

64 55 28,88

—0,02

3-1

3-2

3-5

3-4

0 00 00,00

56 25 37,79

172 53 39,44

282 29 53,83

220 42 14,28

277 07 52,09

33 35 54,67

143 12 07,24

220 42 14,28

220 42 14,30

220 42 15,23

220 42 13,41

220 42 14,30

277 07 52,09

33 35 53,74

143 12 08,13

—0,02

+0,93

—0,89

2,30

2,12

2,17

2,62

+5,85

+9,66

-5,26

—4,72

—6,80

+ 1,21

+7,92

—6,31

220 42 14,30

+0,02

4-1

4—2

4-3

4-5

0 00 00,00

26 09 54,12

46 36 17,98

77 59 46,71

276 35 49,82

302 45 43,26

323 12 07,24

354 35 37,21

276 35 49,82

276 35 49,14

276 35 49,26

276 35 50,50

276 35 49,68

302 45 43,80

323 12 07,66

354 35 36,39

+0,14

—0,54

—0,42

+0,82

3,09

4,36

2,62

3,92

+6,63

+3,98

+4,72

+0,50

+0,77

+2,56

+6,31

+5,24

9°

276 35 49,68

0,00

5-4

5-3

5-2

0 00 00,00

39 00 17,79

70 19 51,51

174 35 37,21

213 35 54,67

244 55 28,92

174 35 37,21

174 35 36,88

174 35 37,41

174 35 37,17

213 35 54,96

244 55 28,68

+0,04

—0,29

+0,24

3,92

2,17

3,64

—0,50

+5,26

+5,13

—5,24

—7,92

—2,40

*°5

174 35 37,17

—0,01

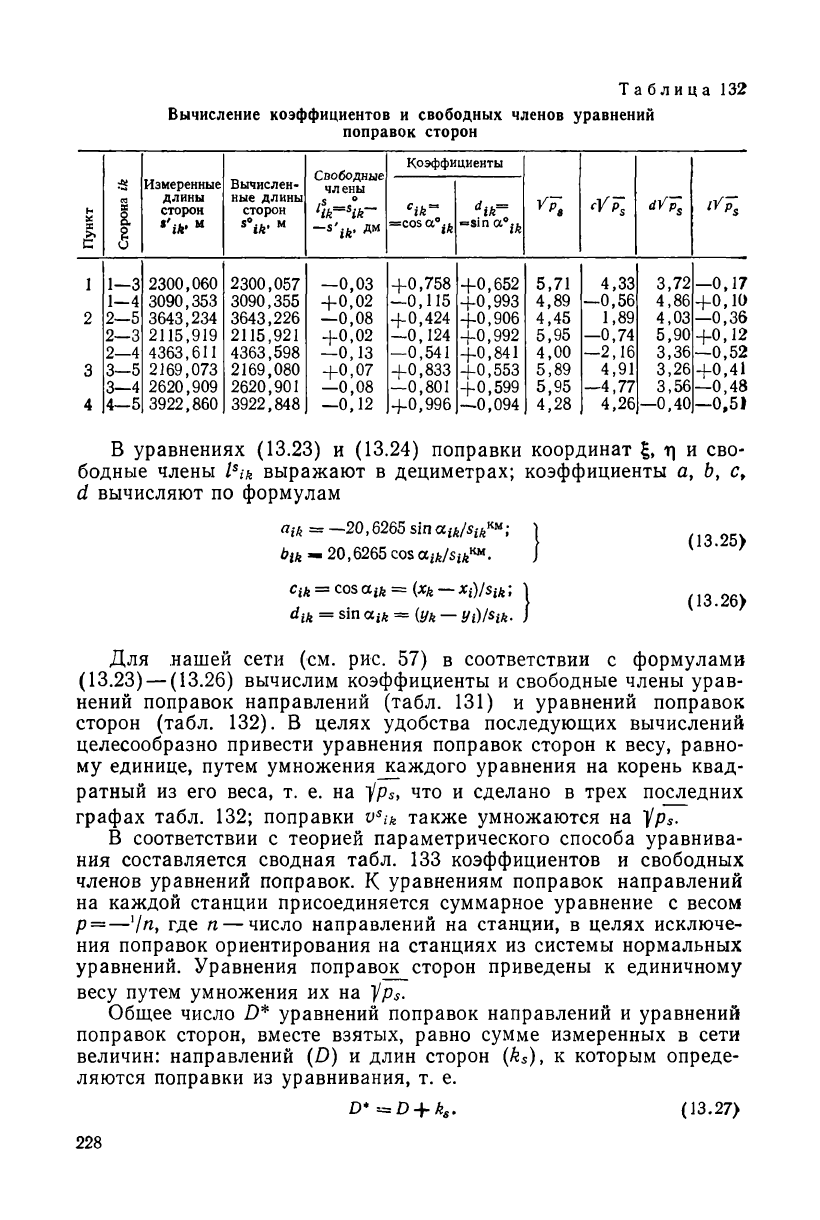
Таблица 126 Таблица 127

Вычисление коэффициентов и свободных членов уравнений

поправок сторон

Измеренные

длины

сторон

''ik-

Вычислен'

ные длины

сторон

ik'

. м

Свободные

чл ены

S °

ik=4k-

—s'

ik•

Коэффициенты

=cos

dVp

1—3

1-4

2-5

2-3

2—4

3-5

3—

4-5

2300,060

3090,353

3643,234

2115,919

4363,611

2169,073

2620,909

3922,860

2300,057

3090,355

3643,226

2115,921

4363,598

2169,080

2620,901

3922,848

—0,03

+ 0,02

—0,08

+0,02

—0,13

+0,07

—0,08

—0,12

+0,758

—0,115

+0,424

—0,124

—0,541

+0,833

—0,801

+0,996

+0,652

+0,993

+0,906

+0,992

+0,841

+0,553

+0,599

—0,094

5,71

4,89

4,45

5,95

4,00

5,89

5,95

4,28

4,33

-0,56

1,89

—0,74

—2,16

4,91

4,77

4,26

3,72

4,86

4,03

5,90

3,36

3,26

3,56

-0,40

—0,17

+0,10

—0,36

+0,12

—0,52

+0,41

—0,48

0,51

В уравнениях (13.23) и (13.24) поправки координат г\ и сво-

бодные члены l

ik выражают в дециметрах; коэффициенты a, b, c

d вычисляют по формулам

= —20,6265 sin a

;

- 20,6265 cos OLik/Sik**

)

k = cosa

k =

(xk

— x

)/s

k; j

= sin a

= (yk

— Уд/Sik.

(13.25)

(13.26)

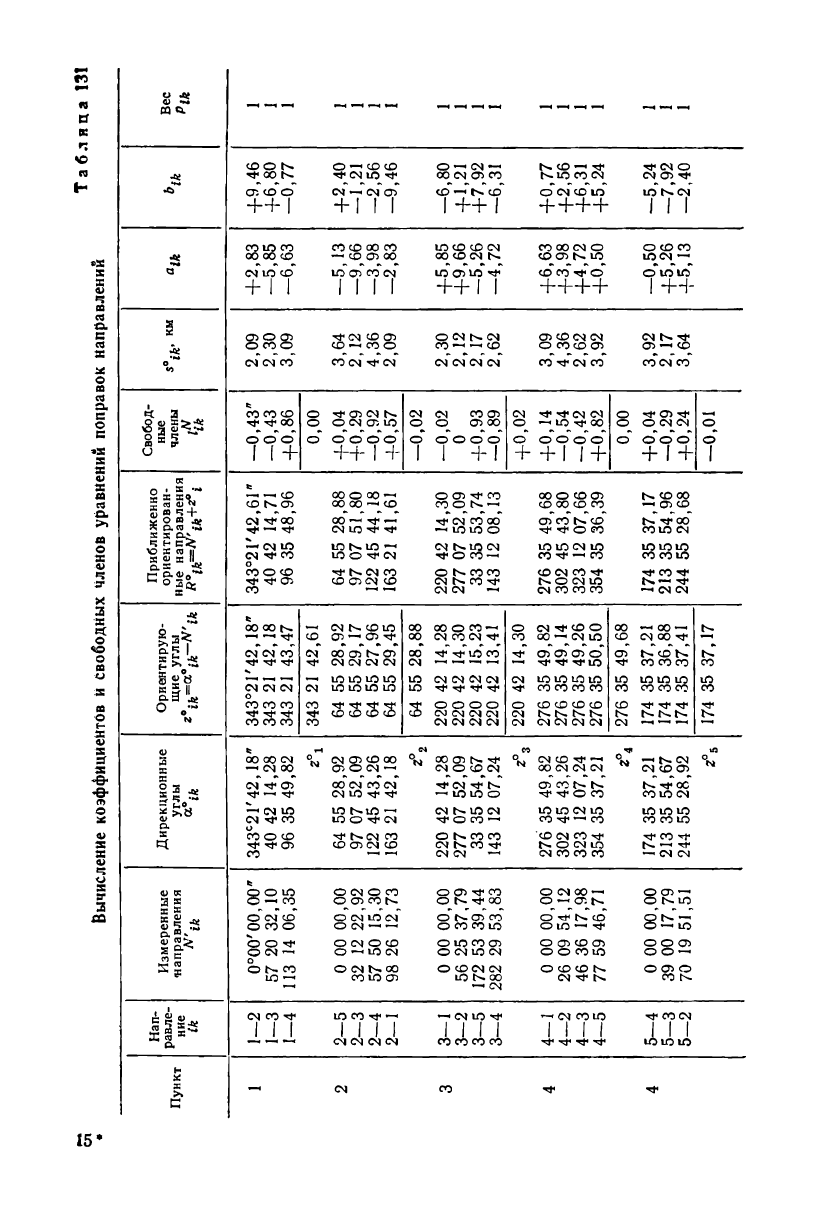
Для нашей сети (см. рис. 57) в соответствии с формулами

(13.23) — (13.26) вычислим коэффициенты и свободные члены урав-

нений поправок направлений (табл. 131) и уравнений поправок

сторон (табл. 132). В целях удобства последующих вычислений

целесообразно привести уравнения поправок сторон к весу, равно-

му единице, путем умножения каждого уравнения на корень квад-

ратный из его веса, т. е. на Уp

, что и сделано в трех последних

графах табл. 132; поправки v

ik также умножаются на Ур*.

В соответствии с теорией параметрического способа уравнива-

ния составляется сводная табл. 133 коэффициентов и свободных

членов уравнений поправок. К уравнениям поправок направлений

на каждой станции присоединяется суммарное уравнение с весом

р =—7п, где п — число направлений на станции, в целях исключе-

ния поправок ориентирования на станциях из системы нормальных

уравнений. Уравнения поправок сторон приведены к единичному

весу путем умножения их на Уд?.

Общее число D* уравнений поправок направлений и уравнений

поправок сторон, вместе взятых, равно сумме измеренных в сети

величин: направлений (D) и длин сторон (k

)

к которым опреде-

ляются поправки из уравнивания, т. е.

+ (13.27)

•228