Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

Схема решения

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

еа

6 378 245,0 м

0 006 69342

г*

6 378 245,0 м

0 006 69342

а(1—*

)

1/6р"

В!

0,25*2

1,25*2

sin В j

sinB

sin Вер

sin

Вг

sin

Вер

0,25*2 sin

0,25*2

sin2

0,25*2 sin

633 5552,717 м

8080228-10-13

49°29'58

938"

45 30 17,221

47 30 08,080

0,00167336

0,00836678

0,71330897

0,76040263

0,73730380

0,50880969

0,57821216

0,54361689

0,00085142

0,00096756

0,00090966

1,25*

sin

Вх

1,25*

sin Вг

1,25*

sin В

ср

1+0,25е

sin

1+0,25*2 sin

Вг

1+0,25*

sin

—1,25е2 sin

1—1,25*

sin

1—1,25*

sin

Вер

Мг

Мер

(В

—Bi)"

(Я

-в,)"/б

0,00425710

0,00483777

0,00454832

1,00085142

1,00096756

J,00090966

0,99574290

0,99516223

0,99545168

6 368 056,324

6 372 511,409

6 370 290,021

14381,717"

0,011620755

444 165,343 м

Контрольные вычисления

{Формулы

(1-е*)

а(

1—б?*)

1/6р"

Вг

В ср

В'ср

Ср

0,25*

1,25*

sin В

sin В'ср

sin В"

sin

Вер

sin

В'ср

sin

В"

ср

(В

СР

~В,)"

(Вср-ВО"^"

Л7,

(Ма+4М'

р+Мср)

17*

Результат вычислений

6 378 245,0 м

0,99330658

6 335 552,717

8080228- Ю-

49°29'58,938"

45 30 17,221

47 30 08,079

48 30 03,508

46 30 12,650

0,00669342

0,00167336

0,00836677

0,73730380

0,74896699

0,72541658

0,54361689

0,56095155

0,52622921

7190,858

0,005810377

6 368 056,324

6 372 511,409

3 822 8413,158

Формулы

0,25е

sin

СР

1,25 г

sin

Вс

1+0.25*

sin

Вер

1—1,25*2 sin

Вер

0,25*2 sin

В'ср

1,25*2 sin

В'ср

1+0,25*2 sin

В'ср

1—1,25*2 sin

В'ср

0,25*2 sin

В" с

1,25*2 sin

В"ср

0,25*2

sin

В"

1—1,25*2 sia

Мер

М' ср

Af'cp

(В

-В

ср

(Вг-В

ср

)"/6р"

(MC

+4M"CP+M

)

Результат

вычислений

0,00090966

0,00454832

1,00090966

0,99545168

0,00093867

0,00469336

1,00093867

0,99530664

0,00088057

0,00440284

1,00088057

0,99559716

6 370 290,021

6 371 402,932

6 369 174,032

7 190,859"

0,005810378

38 215 042,473

222 121,530

222 043,811

444 165,341 м

259

Для контроля вычислений длину дуги параллели следует опре-

делить как разность длин дуг У

и У

отсчитываемых от меридиа-

на с долготой Li—30' (рис. 66). Значения величин Y

и Y\ полу-

чим, пользуясь формулой (15.5):

(/+ 1800)"

~zrr—- Ncos В;

1800"

= —^г—Ncos В.

Искомую дугу параллели получим по формуле

= У

Yi.

Примечания. 1. Точность формулы (15.5) зависит от разно-

сти долгот I. Если /<1°, то, пользуясь восьмизначными таблицами

тригонометрических функций, длину дуги параллели (в средних

широтах) можно получить с ошибкой ±0,001 м. При />1 для

обеспечения указанной точности при вычислении S

нужны табли-

цы с большим числом знаков. Однако в геодезической практике

необходимость в такой точности появляется очень редко. 2. Фор-

мулы (15.3) и (15.6) получены с применением цепных дробей.

Пример 6. Вычисление длины дуги параллели между точка-

ми, лежащими на этой параллели, если даны разность долгот этих

точек

= L

—L

= 0°45

46,882

и широта параллели В = 54°32'19,354".

Решение проверить по контрольной формуле.

Схема решения

Формулы

Результат

вычислений

Формулы

Результат

вычислений

0,25е

0,75е

sin В

sin

0,25е

sin

0,7 5e

sin

0°45'46,882"

54 32 19,354

6 378 245 м

0,00167336

0,00502006

0,81450766

0,66342273

0,00111014

0,00333042

1—0,25е

sin

1—0,75е

sin

cos В

1/р"

N cos В

1"1р"

0,99888986

0,99666958

6 392 453,854 м

0,58015280

2 746,882"

4 848 137-Ю-

3 708 600,002

0,01331726

49388,390 м

Контрольные вычисления

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

Ncos В

1/р"

(/"+1800")/р"

1800"/р"

3 708 600,002

4 848 137- Ю

-12

0,0220439060

0,0087266466

У1

Sn^Vz-Vi

32 363,641

81 752,029

49 388,388 м

§ 84. Вычисление длин сторон

и площади съемочной трапеции

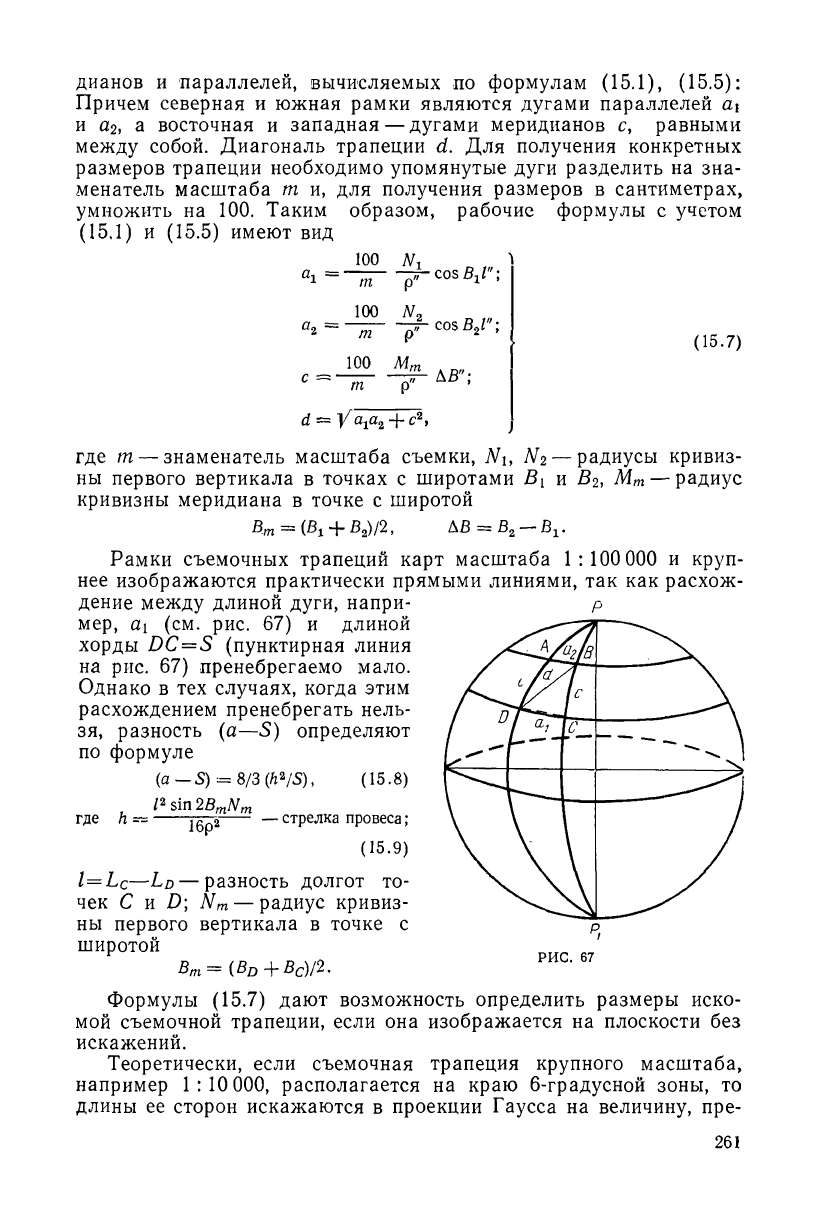
Съемочная трапеция, строго говоря, представляет собой часть

поверхности эллипсоида, ограниченная меридианами и параллеля-

ми (рис. 67). Поэтому стороны трапеции равны длинам дуг мери-

260;

дианов и параллелей, вычисляемых по формулам (15.1), (15.5):

Причем северная и южная рамки являются дугами параллелей а\

и а

а восточная и западная—дугами меридианов с, равными

между собой. Диагональ трапеции d. Для получения конкретных

размеров трапеции необходимо упомянутые дуги разделить на зна-

менатель масштаба т и, для получения размеров в сантиметрах,

умножить на 100. Таким образом, рабочие формулы с учетом

(15,1) и (15.5) имеют вид

с =

100

Р"

100

Р"

ДВ"

(15.7)

где т — знаменатель масштаба съемки, N и N

— радиусы кривиз-

ны первого вертикала в точках с широтами В

{

и В

, Mm — радиус

кривизны меридиана в точке с широтой

Вт = (Bi + В

)/2, ДВ = В

- В

Рамки съемочных трапеций карт масштаба 1:100 000 и круп-

нее изображаются практически прямыми линиями, так как расхож-

дение между длиной дуги, напри- р

мер, а\ (см. рис. 67) и длиной

хорды DC=S (пунктирная линия

на рис. 67) пренебрегаемо мало.

Однако в тех случаях, когда этим

расхождением пренебрегать нель-

зя, разность (а—S) определяют

по формуле

(а — S) = 8/3 (h

/S) , (15.8)

где h

•

sin 2B

16р

— стрелка провеса;

(15.9)

l=L

—L

— разность долгот то-

чек С и О; N

— радиус кривиз-

ны первого вертикала в точке с

широтой

=(B

)/2.

Формулы (15.7) дают возможность определить размеры иско-

мой съемочной трапеции, если она изображается на плоскости без

искажений.

Теоретически, если съемочная трапеция крупного масштаба,

например 1:10 000, располагается на краю 6-градусной зоны, то

длины ее сторон искажаются в проекции Гаусса на величину, пре-

261;

вышающую графическую точность. Линейное искажение определя-

ется формулой

m-l==-2^rcos

(15.1С)

где т — масштаб изображения эллипсоида на плоскости, I — раз*

ность долгот концов рамки съемочной трапеции.

Практически съемка масштабов 1:1 000 000—1:25 000 выпол-

няется с использованием 6-градусной зоны, съемка более крупного

масштаба — с использованием 3-градусной зоны. В указанных слу-

чаях искажения длин рамок съемочных трапеций в проекции Гаус-

са ничтожно малы и ими пренебрегают.

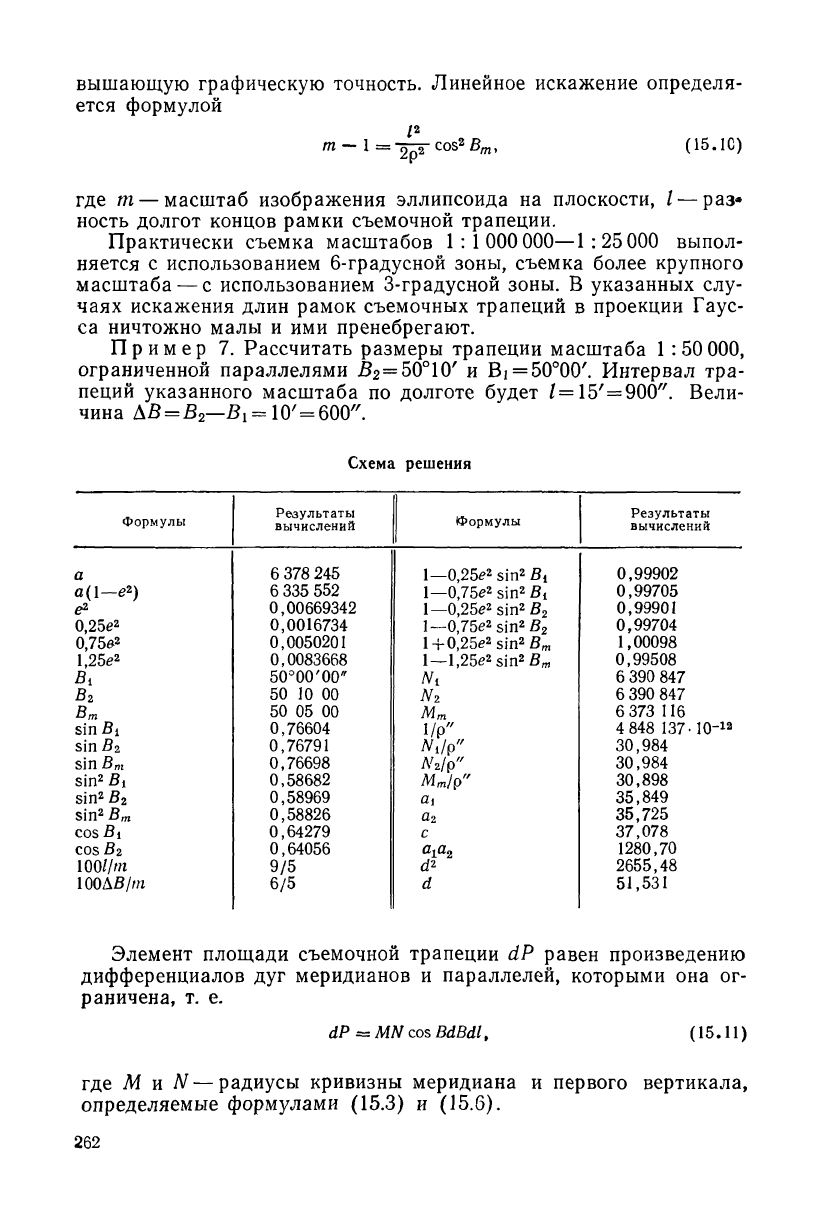
Пример 7. Рассчитать размеры трапеции масштаба 1 :50000,

ограниченной параллелями

= 50

10' И Bi = 50°00'. Интервал тра-

пеций указанного масштаба по долготе будет /=15

=900

. Вели-

чина ДВ = В

—Bi = 10'=600".

Схема решения

Формулы

Результаты

вычислений

(Формулы

Результаты

вычислений

6 378 245

1—0,25*

sin

0,99902

а(1—е

)

6 335 552

1—0,75е

sin

0,99705

0,00669342

1—0,25е

sin

0,99901

0,25е

0,0016734

1—0,75^2 sin

0,99704

0,75в

0,0050201

-г0,25е

sin

1,00098

1,25е

0,0083668

1—1,25<?

sin

0,99508

В t

50°00'00"

6 390 847

Вг

50 10 00

6 390 847

50 05 00

6 373 116

sin В1

0,76604

1/P"

4 848

137 •

Ю-

sin Вг 0,76791

30,984

sin В

0,76698

Л'2/Р"

30,984

sin

0,58682

AWp"

30,898

sin

0,58969

а,

35,849

sin

0,58826

35,725

cos В i

0,64279

37,078

cos B

0,64056

1280,70

1001/tn

9/5

2655,48

100 AB/tn

6/5

51,531

Элемент площади съемочной трапеции dP равен произведению

дифференциалов дуг меридианов и параллелей, которыми она ог-

раничена, т. е.

dP ^MN cos BdBdl. (15.11)

где M и N — радиусы кривизны меридиана и первого вертикала,

определяемые формулами (15.3) и (15.6).

262;

Вводя средний радиус кривизны эллипсоида Я = уЛШ и учиты-

вая, что

2fl)2

получим

с OS В

= (1 —е

sin

В)

2 dBdl

где b — малая полуось референц-эллипсоида Красовского.

Площадь конечной трапеции, ограниченной широтами В

и Вi

и долготами L

и L

выражается двойным интегралом

(1 —е

sin

В)-

cos BdldB.

Интегрируя по L в пределах от L

{

до L

получим

P = b

— LJ j(l - е

sin

В)-

cos

BdB. (15.12)

Раскладывая подынтегральное выражение (15.12) в ряд по би-

ному Ньютона и выполняя затем почленное интегрирование полу-

ченного ряда, будем иметь

Р = Ь

— L

)^sinB

— sin В

+ -у е

(sin

— sin

) +

3 4 1

+ -g- е

(sin

— sin

BJ + — e* (sin

- sin

H . (15.13)

Пользуясь формулой (15.13), можно вычислить площадь ре-

ференц-эллипсоида. В этом случае L

—L\ = 2n

Bi = 0, В

= л/2. На-

пример, площадь эллипсоида Красовского равна Р = 510 083 035 км

Радиус шара, эквивалентного по площади эллипсоиду Красовско-

го, равен £ = 6371 116 м. Поэтому часто для приближенных расче-

тов Землю принимают за сферу радиуса R = 6371 км.

Схема решения

Формулы

Результаты

Формулы

Результаты

Формулы

вычислений

Формулы

вычислений

6356,863

sin

0,15480242

е'г

0,00669342

(2/3) е

0,00446228

1/Р"

4848 137-Ю-

(3/5)е

0,00002688

и-и

1800"

(4/7)^

0,00000017

sin В

0,76977104

0,00002942

sin

Вг

0,45612587

0,00000017

sin

Вг

0,27027622

III 0,0

sin

0,16015148

-L i)"/p"

352 641,9 км

sin В1 0,76604444

40 409 707,2 км

sin

0,44953332

sin sinBx+I +

+ III

0,00375619

sin

Вi

0,26379698

1324,590 км

"-"И

263;

Для вычисления площади съемочной трапеции по формуле

(15.13) необходимо знать широты и долготы параллелей и мери-

дианов, которые ограничивают искомую трапецию заданного мас-

штаба.

Пример 8. Вычисление на эллипсоиде Красовского площади

трапеции масштаба 1:100 000, ограниченной параллелями В

•=50°20' и £i = 50°00' с точностью до 0,001 км

Для удобства вычислений представим формулу (15.13) в виде

—

L,)

Р= — [sin В

— sin

Z?!

+ III],

где

\ = (sin

— sin

);

11 = -g- е

(sin

— sin

);

III = —e

(sin

— sin

(Схема решения приведена на стр. 263).

Глава 16

РЕШЕНИЕ СФЕРОИДИЧЕСКИХ ТРЕУГОЛЬНИКОВ

§ 85. Решение сфероидического треугольника

по теореме Лежандра и способу аддитаментов

Треугольник, образованный геодезическими линиями на поверх-

ности эллипсоида (сфероида), называется сфероидическим тре-

угольником.

Решить треугольник — это значит определить все его элементы

(стороны и углы), в то время как некоторые из них должны быть

известны.

Сфероидический треугольник нельзя решить, используя эле-

ментарные функции. Сторона сфероидического треугольника, на-

пример в триангуляции 1 класса,

имеет длину от 20 до 60 км. В

навигации, космической геодезии,

при связи геодезических сетей

разных стран стороны треуголь-

ников могут достигать сотен ки-

лометров. Несложные теоретиче-

ские расчеты показывают, что, ес-

ли необходимо решить треуголь-

РИС. 68 ник с относительной ошибкой

-8

, то сфероидический треуголь-

ник можно рассматривать как сферический, если его стороны не

превышают 240 км.

264;

В связи с этим в геодезической практике применяют специаль-

ные методы решения таких треугольников: по теореме Лежандра

и способу аддитаментов.

А. Решение сферического треугольника по теореме Лежандра

Способ сферических избытков, предложенный А. Лежандром в

1787 г. (теорема Лежандра), состоит в следующем: каждый из уг-

лов сферического треугольника Л, В и С уменьшают на одну треть

сферического избытка г. В результате этого получают углы плос-

кого треугольника Л

Вi, С\ и, оставляя стороны а, й, с сфериче-

ского треугольника без изменений, решают его как плоский по

теореме синусов (рис. 68). Другими словами, от исходного сфери-

ческого треугольника переходят к соответствующему плоскому

треугольнику с теми же сторонами, но с исправленными углами.

Рабочие формулы

у; = В— -у; = у; (16.1)

t -

е =

а D\\ sin А

{

;

средний радиус кривизны эллипсоида для средней широты В

а Ь с

11 =

sin А

sinBj ~ sinC

fbc

sin Л

= /

'•fDi; D\ =

sin Л sin С

sin В

sin

sin В

6 =/Эц sin B

; c = Diisir\C

;

(16.2)

(16.3)

Пример 9. Решение сферического треугольника ABC звена

триангуляции 1 класса, если даны измеренные, приведенные к

центрам зна сов и спроецированные на поверхность эллипсоида

его углы А =50°20

19,41

, £ = 62° 1244,54",

= 67°26'58,43" и сто-

рона &=44 797,282 м. Средняя широта треугольника В

= 48°12

(см. рис. 68).

Вычисление сферического избытка

/ 0,002533 b

sin A sin С 1426,95

2007,04 sin В 0,884681

sin

0,769831 £>i 1612,95

sin С 0,923542 е 4,086"

sin

sin С 0,710971

Примечания. 1. Величину / можно взять из прил. 1 по ши-

роте В

. 2. При вычислении сферического избытка е длины сто-

рон треугольника выражаются в километрах.

265;

Решение треугольника

Вершина

Измеренные

углы сфе-

рического

треуголь-

ника

Поп-

равка

из

урав-

нива-

ния

—w/3

Уравненные

углы сфери-

ческого тре-

угольника

~~ 3

Углы плоского

треугольника

Синусы уг-

лов плоско-

го треуголь-

ника

62°12'44,54"

50 20 19,41

67 26 58,43

0,57

62°12'45,1Г

50 20 19,98

67 26 59,00

—1,36"

— 1,36

—1,37

62°12'43,75"

50 20 18,62

67 26 57,63

0,88467988

0,76982866

0,92354082

w=— (е +

+ 180)+2

180 00 02,38

04,09

—01,71

180 00 04,09

180 00 00,00

Стороны сферического треугольника

Dn 50 636,714 м а 38 981,594 м

b 44 797,282 м с 46 765,073 м

Б. Способ аддитаментов

В основе способа аддитаментов, предложенного И. Зольднером

в 1820 г., лежит теорема синусов (см. рис. 68)

sina//? sin b/R slnc/R

sin4

sin В

sin С *

(I6

Ввиду малости величин a/R

b/R> c/R> выражающих стороны

сферического треугольника в радианной мере, по сравнению с ра-

диусом Земли /?, синусы этих величин можно разложить в ряд.

Ограничиваясь двумя членами разложения, получим

а —а

/6/?

6 — Ауб/?

— c?/6R

sin

— sin В — sinC '

Идея способа аддитаментов заключается в том, что стороны

сферического треугольника а, Ь, с исправляют поправками, в ре-

зультате чего получают стороны плоского треугольника а\ Ъ', с'

и неизвестные стороны сферического треугольника.

При этом, в логарифмическом варианте, аддитаментами назы-

вают поправки в логарифм стороны Л

, Аь

. В случае нелога-

рифмического решения, как видно из (16.5), аддитаментами яв-

ляются величины

= ka

; A

= W\ A

k<*\

где й=1/6R

/? =

УМЛ

— средний радиус кривизны эллипсоида для

района расположения треугольника.

Рассмотрим последовательность решения сферического тре-

угольника по способу аддитаментов.

1. Из исходной стороны b вычитают ее аддитамент Аъ и полу-

чают сторону плоского треугольника Ь\

266;

2. По известным углам сферического треугольника и стороне Ъ'

решают треугольник как плоский, используя теорему синусов, и

находят остальные стороны плоского треугольника а' и с\

3. Полученные значения сторон исправляют их аддитаментами

и А

и находят искомые стороны сферического треугольника

ABC.

Способ аддитаментов применяется как контрольный при реше-

нии треугольников по теореме Лежандра.

а' =

Рабочие формулы

b' ~ ь — Аь ~

— kb

= kb*

sin Л a'sin С

sin В ' sin

a = a' + ka'

= a' + Л

; с = с' + kc'

= с + Л

;

= ka'

\ А

— kc'

;

k= 1/6RK

(16.6)

(16.7)

(16.8)

(16.9)

(16.10)

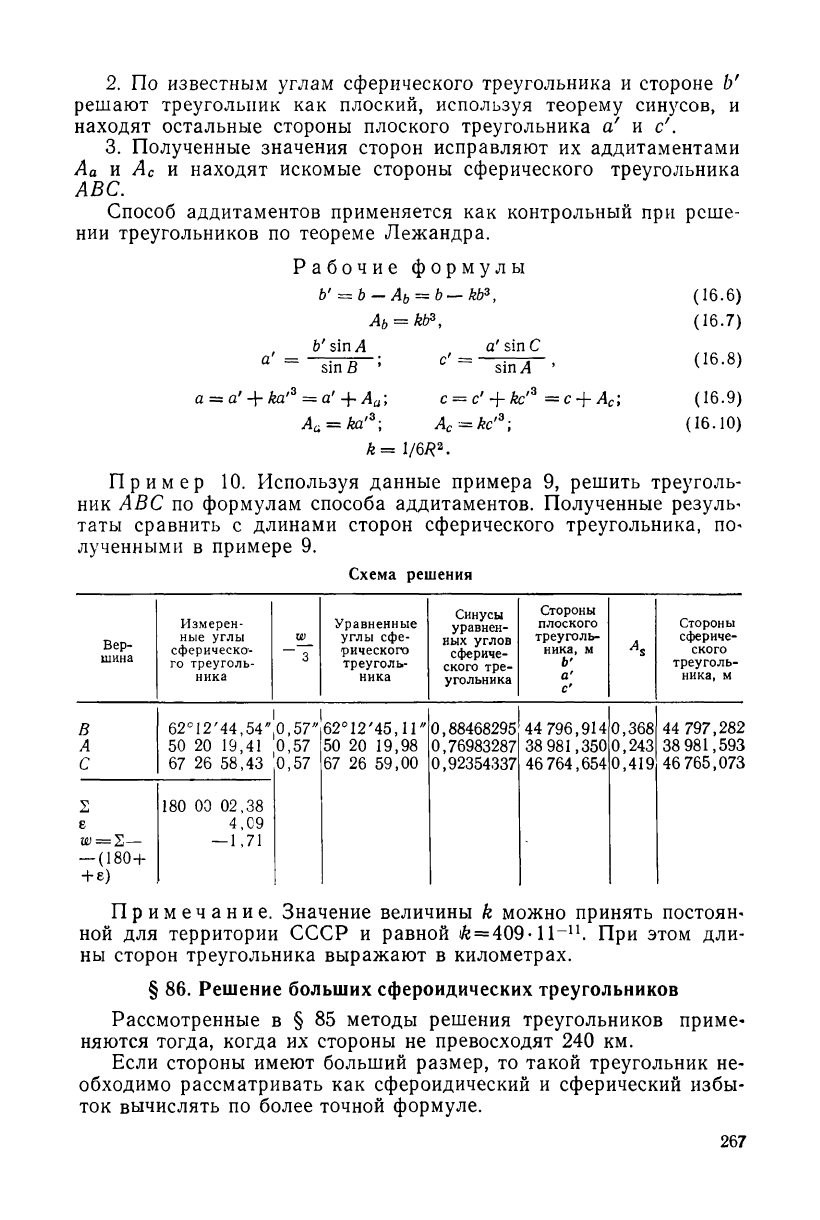
Пример 10. Используя данные примера 9, решить треуголь-

ник ABC по формулам способа аддитаментов. Полученные резулы

таты сравнить с длинами сторон сферического треугольника, по-

лученными в примере 9.

Схема решения

Вер-

шина

Измерен-

ные углы

сферическо-

го треуголь-

ника

~ 3

Уравненные

углы сфе-

рического

треуголь-

ника

Синусы

уравнен-

ных углов

сфериче-

ского тре-

угольника

Стороны

плоского

треуголь-

ника, м

Ь'

а'

с'

Стороны

сфериче-

ского

треуголь-

ника, м

62°12'44,54"

50 20 19,41

67 26 58,43

1 1

,0,57"

,0,57

0,57

62°12'45,11"

50 20 19,98

67 26 59,00

0,88468295

0,76983287

0,92354337

44 796,914

38 981,350

46 764,654

0,368

0,243

0,419

44 797,282

38 981,593

46 765,073

— (180 +

180 00 02,38

,С9

—

,71

1 1

,0,57"

,0,57

0,57

62°12'45,11"

50 20 19,98

67 26 59,00

0,88468295

0,76983287

0,92354337

44 796,914

38 981,350

46 764,654

0,368

0,243

0,419

44 797,282

38 981,593

46 765,073

Примечание. Значение величины k можно принять постоян-

ной для территории СССР и равной й = 409-11

-11

. При этом дли-

ны сторон треугольника выражают в километрах.

§ 86. Решение больших сфероидических треугольников

Рассмотренные в § 85 методы решения треугольников приме-

няются тогда, когда их стороны не превосходят 240 км.

Если стороны имеют больший размер, то такой треугольник не-

обходимо рассматривать как сфероидический и сферический избы-

ток вычислять по более точной формуле.

267;

Общий подход к решению сфероидических треугольников мож-

но представить следующим образом.

Пусть даны углы сфероидического треугольника Л, В, С, ис-

ходная сторона Ъ (см. рис. 68), широты вершин треугольника В А,

, Вс и средняя широта расположения треугольника В

. Требует-

ся определить другие стороны треугольника.

Углы сфероидического треугольника можно представить в виде

Л = Л

сф

+ 6Л; В = В

сф

+ 6В; С С

ф + 6С, (16.11)

где Л

ф, В

ф, С

ф — сферические углы треугольника; б Л, бВ, 6С —

поправки за сфероидичность треугольника.

Поправки за сфероидичность вычисляются по формулам

6Л

(16.12)

1 1

где К~ (МЩ гауссова кривизна эллипсоида на средней

широте расположения треугольника,

КА> КВ> КС

— гауссовы кри-

визны эллипсоида в вершинах рассматриваемого треугольника,

М, N — радиусы кривизны эллипсоида, вычисляемые по форму-

лам (15.3) и (15.6).

Определив поправки за сфероидичность по формулам (16Л2),

перейдем к сферическим углам треугольника на основании (16Л1)

ф = А — бА; £

сф

= £ — 6В; С

сф

= С —6С. (16.13)

На основании исходных данных и сферических углов опреде-

лим приближенное значение сферического избытка

sin Л

сф

sin С

сф

пр = / >

где /=р"/2/?

т>

Rm — средний радиус кривизны эллипсоида на ши-

роте Вт.

После этого приближенно определим углы плоского треуголь-

ника по известным формулам теоремы Лежандра:

= Лф

—

е/3; В

= В

сф

— е/3; С

« С

сф

—

г/3.

На основании теоремы синусов определим приближенные зна-

чения искомых сторон

а = Dusw Ai;

= Dj

sinB

; с— DnsinC^

Таким образом, сначала решаем треугольник по теореме Ле-

жандра и полученный результат используем как приближенный

для последующего уточнения. А именно: из сферической тригоно-

метрии известна точная формула для определения сферического

и з б ы т к а

е/4 = tg (р/2) tg [(р -

а)/21

[(р —b)/2]

tg [(р - с)/2] , (16.14)

где а, Ь, с — стороны треугольника в градусной мере,

(а

+ с)/2.

268;