Xin Q. Diesel Engine System Design

Подождите немного. Документ загружается.

256 Diesel engine system design

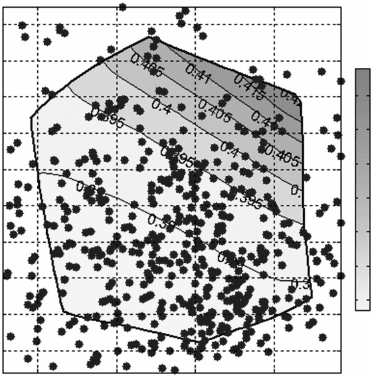
domain, which is represented by ‘air–fuel ratio vs. EGR rate’ (Fig. 3.18).

Figure 3.19 shows the DoE raw data of coolant heat rejection and BSFC

plotted in the response domain without using the emulators or optimization.

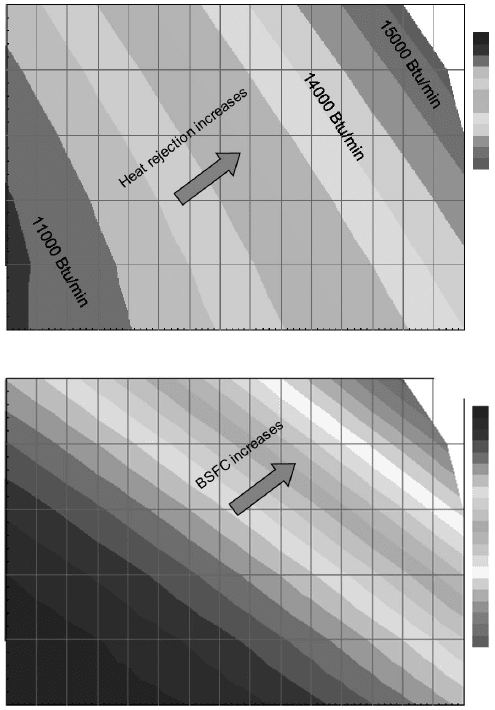
Figure 3.20 shows the optimized coolant heat rejection (in the sense of

minimum BSFC) and BSFC by using the emulators. It is observed that Figs

3.19 and 3.20 give totally different data trends in heat rejection and BSFC. It

shows that without optimization the raw DoE data can be misleading in the

data trend because the factor settings used in a DoE matrix do not guarantee

any trend in the raw data. The DoE factors used in this example include

fuel injection timing, EGR valve opening, VGT vane opening, turbocharger

efciency, EGR cooler size, and charge air cooler size. This example shows

the importance of using DoE emulator to process the DoE raw data and

conduct optimization.

The information on parametric sensitivity of system response, generated

either analytically or graphically, is often even more valuable than a single

set of estimated optimum solutions. The theoretical advantages of ridge

analysis, canonical eigenvalues, and the technique of optimum contour map

can be combined in the future to generate a more powerful analysis tool for

the RSM DoE design, optimization, and data display. This is an important

research direction for optimization in diesel engine system design.

BSFC (lb/(hp.hr))

20 25 30 35

EGR rate (%)

A/F ratio (–)

0.42

0.415

0.41

0.405

0.4

0.395

0.39

3.18 Illustration of raw DoE data and minimum BSFC optimization

contours.

Diesel-Xin-03.indd 256 5/5/11 11:46:06 AM



257Optimization techniques in diesel engine system design

3.3 Advanced design of experiments (DoE)

optimization in engine system design

3.3.1 Engine optimization with the Taguchi method

There are numerous studies using the Taguchi method in engine design and

testing applications. The engine performance related design and calibration

work is reviewed here. Baranescu et al. (1989) from Navistar used the

Taguchi method and engine cycle simulation to analyze the effects of control

factors and noise factors on diesel engine power. The analysis started with

the cause-and-effect ‘shbone’ diagram to brainstorm design factors. Five

Engine coolant heat rejection

BSFC (lb/(hp.hr))

10000 Btu/min

15.0 16.0 17.0 18.0 19.0 20.0 21.0 22.0 23.0 24.0 25.0 26.0 27.0 28.0 29.0

EGR rate (%)

15.0 16.0 17.0 18.0 19.0 20.0 21.0 22.0 23.0 24.0 25.0 26.0 27.0 28.0 29.0

EGR rate (%)

A/F ratio

27.0

26.0

25.0

24.0

23.0

22.0

21.0

20.0

19.0

18.0

17.0

16.0

27.0

26.0

25.0

24.0

23.0

22.0

21.0

20.0

19.0

18.0

17.0

16.0

MAX: 14203

MIN: 10318

MAX: 0.423

MIN: 0.380

Coolant heat

rejection (Btu/min)

10000

10200

10400

10600

10800

11000

11200

11400

11600

11800

12000

12200

12400

12600

12800

13000

13200

13400

13600

13800

14000

14200

14400

14600

BSFC

(lb/(hp.hr))

0.375

0.380

0.385

0.390

0.395

0.400

0.405

0.410

0.415

0.420

0.425

3.19 Raw DoE output data in response domain without optimization.

14000 Btu/min

Diesel-Xin-03.indd 257 5/5/11 11:46:07 AM



258 Diesel engine system design

control factors (turbocharger build, intake ow area, exhaust ow area, intake

cam, and exhaust cam) and four noise factors (ambient temperature, engine

compression ratio, injection timing, and fueling rate) were selected. Most

factors were set at three levels. They used an inner array for the control

factors and an outer array for the noise factors. The signal-to-noise ratio of

engine power was evaluated along with the mean value of engine power. They

used the main effect plot to identify strong factors and weak factors. The

interaction effect of two control factors, turbocharger build and intake ow

Optimized engine coolant heat rejection in the A/F ratio vs. EGR rate domain

at 3300 rpm rated power, optimization to minimize BSFC with the constraints

of ﬁxed compressor efﬁciency 72%, turbine efﬁciency 65%, EGR cooler

effectiveness 80%, and CAC effectiveness 90%

15.0 16.0 17.0 18.0 19.0 20.0 21.0 22.0 23.0 24.0 25.0 26.0 27.0 28.0 29.0 30.0

EGR rate (%)

15.0 16.0 17.0 18.0 19.0 20.0 21.0 22.0 23.0 24.0 25.0 26.0 27.0 28.0 29.0 30.0

EGR rate (%)

A/F ratio

25.0

24.0

23.0

22.0

21.0

20.0

25.0

24.0

23.0

22.0

21.0

20.0

MAX: 15697

MIN: 10873

MAX: 0.232

MIN: 0.034

Coolant heat

rejection (BTU/min)

10000

10500

11000

11500

12000

12500

13000

13500

14000

14500

15000

15500

16000

0.030

0.040

0.050

0.060

0.070

0.080

0.090

0.100

0.110

0.120

0.130

0.140

0.150

0.160

0.170

0.180

0.190

0.200

0.210

0.220

0.230

0.240

BSFC penalty over

a baseline engine

3.20 Optimized DoE output data in response domain by using RSM

emulators.

Diesel-Xin-03.indd 258 5/5/11 11:46:07 AM



259Optimization techniques in diesel engine system design

area, was considered when a proper inner array L

was selected. Possible

trade-offs between the mean value and the signal-to-noise ratio of the engine

power were pointed out and demonstrated by using their main effect plots

side-by-side as a multi-objective optimization. Optimum control factor levels

were selected for the best power (i.e., large mean) and robustness (i.e., large

signal-to-noise ratio). The ANOVA study of the signal-to-noise ratio was

provided including the interaction effect between the control factors. An

estimate of cost savings due to the optimized design was also provided. This

work is an important pioneering analysis of using the Taguchi DoE method

on engine performance. It applied many important concepts of robust design

and optimization in engine simulation applications.

Another important optimization work on diesel combustion and transient

emissions using the Taguchi DoE method combined with the Monte Carlo

simulation was reported by Navistar’s Yan et al. (1993). Four important

concepts were introduced to the area of optimization of diesel engine emissions

and performance. They are: (1) measured signal-to-noise ratio for each DoE

run; (2) transient optimization; (3) multi-objective optimization for multiple

combustion parameters (PM, NO

, HC, INSOL, SOF, and CBSFC); and (4)

probability distribution sampling for analyzing the variability of production

emissions with the Monte Carlo simulation. Understanding the statistical

distribution of production emissions and reducing both the mean and the

standard deviation of the transient emissions were the objectives of their

analysis. Six control factors with three levels on each factor were selected in

a single L

array: piston-to-head clearance, nozzle ow, nozzle protrusion,

spray cone angle, injection timing, and injection control pressure. Because it

was an experimental work, they selected sufciently wide intervals between

the factor levels in order to cover three times the standard deviation of each

design factor. The signal-to-noise ratio was used as an optimization response

parameter to minimize the emissions variance by using the main effect plot.

Unlike the signal-to-noise ratio calculation conducted by Baranescu et al.

(1989) who used an inner L

control factor array and an outer L

noise

factor array, Yan et al. (1993) used engine transient measurements to obtain

the mean, the variance, and the signal-to-noise ratio for each L

DoE run.

Each emission data in a DoE run is a summary point from the transient

measurement. In contrast, Baranescu et al. (1989) used the outer array design

points at a given inner array factor setting to compute the signal-to-noise

ratio for each L

run (as illustrated in Fig. 3.4) with steady-state engine

cycle simulations. Yan et al. (1993) used the main effect plot to check the

sensitivity of signal-to-noise ratio as a response with respect to all six control

factors for six performance/emissions parameters. The data exhibited fairly

nonlinear behavior of the signal-to-noise ratios with respect to the factor

levels. The optimum factor setting was selected with the highest signal-

to-noise ratio for each factor meanwhile minimizing the mean of PM and

Diesel-Xin-03.indd 259 5/5/11 11:46:07 AM



260 Diesel engine system design

maintaining the mean of NO

at a constant level. They also illustrated the

method of calculating the optimum signal-to-noise ratio at 95% condence

interval and the estimated optimum response (emissions) values. The 95%

condence interval level is usually a good compromise between model

accuracy and complexity. A high signal-to-noise ratio does not necessarily

mean the statistical distribution of the emissions variability is acceptable. The

authors continued their investigation by using the Monte Carlo simulation

along with the emissions regression models obtained from an earlier step

and other relevant models to calculate the statistical distributions of the

emissions parameters for ten factors. The ten factors were: nozzle cone angle,

nozzle protrusion, piston-to-head clearance, head gasket thickness, stem seal

leak rate, oil contribution from other sources, timing, injection command

pressure, nozzle ow, and intake port swirl ratio. The statistical distributions

of the input factors were determined by actual engine testing data. A large

amount of samples were taken as the input for the Monte Carlo simulation.

The Monte Carlo simulation was run 500 times to obtain the result of

emissions variability/scattering. They quantied the contribution from each

factor on the standard deviation of the emissions distributions. This work

leaped from the Taguchi DoE method of signal-to-noise ratio optimization

to probability distribution analysis for performance variability, and it is one

of the pioneering works in the Monte Carlo simulation for diesel engines.

Hunter et al. (1990) applied the Taguchi method to simultaneously optimize

several diesel engine design and operating parameters for low emissions in

a single cylinder engine. The control factors included engine compression

ratio, nozzle area, nozzle protrusion, boost pressure, start-of-combustion

timing, indicated mean effective pressure, and engine speed. The interactions

included: compression ratio vs. nozzle area, compression ratio vs. nozzle

protrusion, and nozzle area vs. nozzle protrusion. The responses included

the mean and the signal-to-noise ratio of particulate matter, NO

, HC, and

smoke. They provided a detailed description of each step in the Taguchi

method, especially the calculation procedure and formula for predicting

the optimum responses (with 90% condence interval) when each factor is

independent and no signicant interactions exist. Gardner (1992) used the

Taguchi method to investigate the effects of changes in fuel spray cone angle,

number of spray holes, nozzle hole area, nozzle tip protrusion, compression

ratio, swirl level, and fuel injection timing on diesel engine combustion and

emissions. He pointed out that, although the Taguchi method is a powerful

tool for factor screening and optimization, it should be used with caution

to understand the confounding and interaction effects in order to choose

an appropriate orthogonal array and to avoid erroneous conclusions drawn

from the main effect study. Win et al. (2002) used the Taguchi method to

conduct an experimental study on diesel engine noise, emissions, and fuel

economy. They used the signal-to-noise ratio and ANOVA to quantify the

Diesel-Xin-03.indd 260 5/5/11 11:46:07 AM



261Optimization techniques in diesel engine system design

inuence of engine speed, load, and fuel injection timing on performance

response parameters.

Interesting experimental work was carried out by Yamamoto et al. (2002)

by combining the Taguchi method (orthogonal array design and linear

graph) with RSM (polynomial surface-t empirical model) to optimize the

parameters in fuel injection, turbine and EGR systems for low NO

, PM

emissions, and BSFC for a heavy-duty diesel engine. Their work is important

for the following four contributions: (1) expanding the DoE optimization

from a single speed–load mode to balancing all 13 modes in a steady-state

emissions cycle; (2) checking optimization results against design constraints;

(3) combining Taguchi’s orthogonal array design with a special polynomial

model; and (4) using a Chebychev’s orthogonal polynomial as an empirical

model in the Taguchi method. In their study, six calibration or design factors

with three levels were used in a Taguchi L

orthogonal array: VGT vane

opening, EGR valve lift, injection timing, common rail injection pressure,

injection nozzle diameter, and injection nozzle cone angle. The DoE method

was applied at each engine mode point of the Japanese 13-mode emissions

test cycle. After the optimum trade-off between the emissions and the BSFC

at each mode point was obtained, the optimization for the entire 13-mode

composite was made by a balancing between the modes. They used ANOVA

to quantify the interaction effects among VGT vane opening, EGR valve lift,

and fuel injection timing. It should be noted that they used a Chebychev’s

orthogonal polynomial, rather than a regular second-order polynomial, to

t a second-order empirical model including the interaction terms. In most

other researchers’ work using the Taguchi method, the main effect plot, the

signal-to-noise ratio and condence interval were usually used to identify

the optimum factor levels and estimate the optimum responses. Yamamoto

et al. (2002) did not take that approach. They used Chebychev’s empirical

equation to conduct a numerical parametric study at each mode. They took

this different approach probably in an attempt to overcome the weakness of

the Taguchi method in regression models. Checking the predicted optimization

solution against design constraints was particularly mentioned in their work.

The limiting constraints included smoke, turbocharger over-speed, engine

over-speed, exhaust gas temperature, and maximum cylinder pressure. The

authors probably did not realize that their work actually took a hybrid approach

between the Taguchi method and RSM. Although it is worthwhile to further

investigate the validity of using a low-resolution Taguchi orthogonal array

with polynomial surface-t, their attempt of using a Chebychev’s orthogonal

polynomial, which is a special polynomial, did indicate an opportunity worth

further exploration in engine optimization theory.

The above examples show that the Taguchi DoE method has been

successfully used in diesel engine performance development. The

previous efforts have laid out a good foundation for this area to move

Diesel-Xin-03.indd 261 5/5/11 11:46:07 AM



262 Diesel engine system design

forward to adopt the more advanced DoE optimization theories and

techniques.

3.3.2 Engine calibration with RSM

Engine performance and emissions calibration is probably the area where

the RSM DoE technique has been most widely used compared with other

engine application areas. Engine calibration refers to tuning mechanically

or electronically the adjustable parameters on the engine to reach desirable

performance. In contrast to hardware design where a xed sizing has to be

chosen from a few candidates (e.g., engine compression ratio, turbine area,

cooler size), a tunable parameter offers the exibility of varying within a

range, depending on different engine speed and load operating conditions or

ambient conditions. Examples of mechanical tuning device include mechanical

governor, mechanical fuel injection system, and pneumatically controlled

turbine wastegate. Since electronic controls were applied to diesel engines

starting in the 1990s, the exibility and performance of the engine have

been greatly improved. However, the complexity of engine calibration and

the associated complexity in electronic control strategies and software have

increased dramatically. There are many electronically controlled calibration

parameters available in the engine, for example fuel injection timing, injection

pressure, turbine wastegate opening, VGT vane opening, EGR valve opening,

and intake throttle opening. Other possible calibration parameters include

cooling control valve setting, variable valve timing or cam phasing angle,

variable swirl control, and cylinder deactivation. Without using a DoE, nding

the optimum setting for these calibration factors is almost impossible.

Roepke and Fischer (2001) introduced an efcient calibration method

on variable valvetrain by using RSM for a gasoline engine. They pointed

out that the D-Optimal is very suitable and efcient for engine calibration

due to its capability of handling the constraints in factor combinations. The

concept of model-based calibration was explained by Lumsden et al. (2004)

in their RSM DoE work for stratied charge direct injection gasoline engines.

They indicated that using a third-order model with the space-lling DoE

design may yield better predictability than using the second-order model for

hydrocarbons and BSFC. Mallamo et al. (2004) used RSM to optimize an

off-road common-rail diesel engine performance with four calibration factors

(main injection timing, pilot injection duration, pre-injection timing, and

pre-injection duration) at three levels for each factor. The optimization was

conducted for NO

, PM, noise, and BSFC. It was proved that the model built

based on the CCF design gave very similar results to the model built based

on the full factorial design. Diesel engine calibration with DoE optimization

techniques was also reported by Brooks et al. (2005).

Engine calibration has been moving in the direction of using RSM DoE

Diesel-Xin-03.indd 262 5/5/11 11:46:07 AM



263Optimization techniques in diesel engine system design

with online automated testing, dynamic mapping, and ofine optimization, as

summarized by the MathWorks hosted SAE Panel Discussion (The MathWorks,

2007). Moreover, the powerful approach proposed earlier by using the two-

dimensional minimum BSFC contour maps can greatly enhance the quality

and efciency of optimization work in both engine calibration and engine

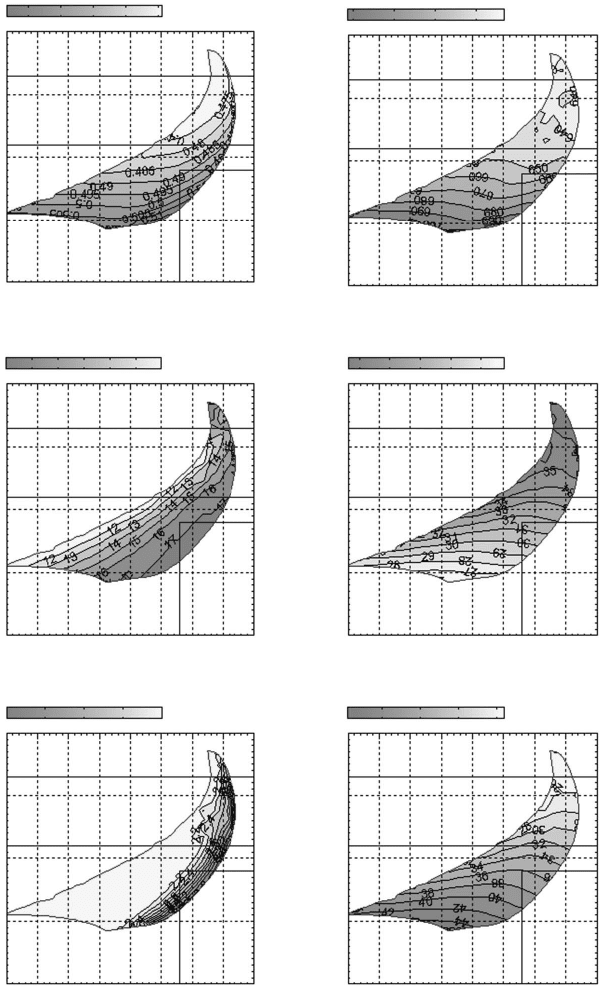
system design. Figure 3.21 shows an example of applying the approach of

minimum BSFC contour maps to the DoE optimization of engine emissions

calibration. Note that the factors and responses in the gure are all optimized

in the entire map domain with the minimum BSFC. The boundary of the

‘soot vs. NO

’ response domain is formed by the factor range of the DoE

and the calibration constraints.

3.3.3 Engine system optimization with RSM

Diesel engine system design is conducted by using DoE optimization

based on numerical simulation data since simulation can greatly reduce the

cost and time of hardware testing during engine development. The control

factors and noise factors can be brainstormed by using the cause-and-

effect ‘shbone’ diagram, as shown in Fig. 3.22 for engine performance

simulation. Figure 3.22 shows all the important categories of factors in an

engine performance model. The control factors may include hardware sizing

or engine calibration parameters. The noise factors can be from piece-to-

piece variation, environmental conditions, customer usage, or deterioration

over time. A large number of DoE optimization examples in diesel engine

system design are provided in Chapter 15 where the effects of subsystem

interaction are thoroughly addressed.

It is worth noting that RSM was used by Dvorak and Hoekstra (1996) more

than a decade ago for optimizing internal combustion engine performance.

Recognizing the weakness of the Taguchi method in quantifying the

interaction effects between engine performance factors, they used the central

composite design in RSM and engine performance simulation to analyze

the effects of eight design factors (intake valve diameter, exhaust valve

diameter, intake runner length, intake beginning runner area, bore, stroke,

intake cam duration, and exhaust cam duration) on engine power for a

gasoline engine. A second-order regression model including the interaction

effects were used. The optimization of engine power was conducted using

the method of steepest ascent. It should be noted that a canonical analysis

was performed to identify the canonical axis along which the greatest rate

of change occurred for the engine power. A stationary point was derived

as the optimum solution for the maximum engine power within the design

space. It was pointed out by the authors that the principal axis information

obtained from the canonical analysis was utilized to identify and construct

the new factor range of an expanded DoE in order to further increase the

Diesel-Xin-03.indd 263 5/5/11 11:46:07 AM



BSSoot (g/(hp.hr))

BSSoot (g/(hp.hr))BSSoot (g/(hp.hr))

BSSoot (g/(hp.hr))

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

0.4

0.35

0.3

0.25

0.2

0.15

0.1

0.05

3.5

2.5

0.51

0.5

0.49

0.48

0.47

700

680

660

640

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

0 0.5 1 1.5 2

BSNO

(g/(hp.hr))

Main injection timing (degree ATDC) Fuel injection pressure (MPa) BSFC (lb/hp.hr)

EGR rate (%) Air–fuel ratio

Exhaust manifold temperature

(°F)

3.21 HD diesel engine steady-state emissions calibration optimization with DoE and RSM (mode B25).

Diesel-Xin-03.indd 264 5/5/11 11:46:08 AM



Engine responses:

• Power

• BSFC

• Cylinder pressure

• Cylinder gas

temperature

• Intake and exhaust

manifold pressures

• Compressor outlet

air temperature

• Manifold gas T

• Exhaust gas

temperature

• Air ow rate

• EGR ow rate

• Fuel ow rate

• Emissions

• Heat rejections

• Reciprocating

forces

The brainstorming of

factors-causes covers

a system level and

the needs from all

subsystems.

Vehicle drivetrain

Hybrid powertrain

Cylinder head

Valvetrain

Connecting rod

Crankshaft

Exhaust manifold

Turbocharger

EGR system

Fuel system

Cooling system

Waste heat recovery

Engine brake

Accessories

Aftertreatment

Engine controls

Engine calibration

Intake manifold

Power cylinder &

piston assembly

Combustion and heat release

Cylinder breathing (volumetric efﬁciency)

Engine friction

Base engine heat rejection characteristics

Exhaust pipe heat transfer

Airpath control strategy

Air system controls and calibration

Engine basic geometry

Altitude and ambient pressure

Engine inlet air temperature

Engine operating condition

Engine ﬂow restrictions

Turbocharger

Charge air cooler (CAC)

EGR cooler

Compressor inter-stage cooler (ISC)

Bore

ROA

Ambient

temperature

Engine

speed

Engine

load

(fueling)

Exhaust

restriction

Compressor

efﬁciency

Turbine

efﬁciency

Intake

restriction

Stroke

Masses

Turbine

area

CAC

ﬂow

restriction

EGR

cooler

ﬂow

restriction

EGR

cooler

size

EGR

cooler

sink T

ISC

sink T

ISC

size

CAC

size

CAC

sink T

ISC

ﬂow

restriction

Injection

timing

Heat

transfer

areas

Map

set

point

Turbine

wastegate

opening

Piston

skirt

Piston

rings

Valve

size

Intake

port

heating

Insulation

Injection

pressure

Port ﬂow

coefﬁcient

Compression

ratio

Swirl

Bearings

Friction

Vehicle

speed

(cooling

air ﬂow)

Accessories

Swirl

Cylinder

sink T

Piston

cooling

Model

based

EGR

valve

opening

Intake

throttle

opening

3.22 Cause-and-effect diagram for engine system performance analysis.

Intake and

exhaust

cam

proﬁles

Diesel-Xin-03.indd 265 5/5/11 11:46:08 AM

