Xin Q. Diesel Engine System Design

Подождите немного. Документ загружается.

276 Diesel engine system design

the probability distribution of a real-valued random variable. The kurtosis is

equal to the fourth moment-generating function about the mean. Kurtosis is a

measure of the sharpness of the peak and the size of the tail of the probability

distribution. Higher kurtosis means the mean and extreme deviations occur

with higher probability, and the distribution has a sharper peak and longer

or fatter tails. Excess kurtosis is dened as kurtosis minus three, a correction

to make the kurtosis value of the normal distribution equal to zero.

In general, the probability density function and the shape of a statistical

distribution can be described by one or more of the following parameters:

location parameter, scale parameter, shape parameter, or degrees of freedom

parameter. The effect of the location parameter is to translate or shift the

distribution curve horizontally. The effect of the scale parameter is usually

to stretch or shrink the curve horizontally and vertically. The shrinking

approaches a spike as the scale parameter goes to zero. Usually, non-

positive scale parameters are not allowed. Any particular type of probability

distribution is not a single distribution, but in fact a family of distributions.

This is because the distribution has one or more shape parameters. Shape

parameters allow a distribution to form a variety of shapes, depending on

the value of the shape parameter. The combined use of the above statistical

distribution parameters makes the probability distributions particularly useful

in modeling applications since they are exible enough to model a variety

of data sets. The ‘standard’ form of any distribution is the form that has the

location parameter equal to zero and the scale parameter equal to one. The

statistical distribution parameters are extensively used in the nondeterministic

optimization of diesel engine system design (Fig. 3.9).

Analytical relationships between probability distributions

The probability density function of the sum of two independent random

variables is the convolution of each of their probability density functions.

The probability density function of the difference of two independent random

variables is the cross-correlation of each of their probability density functions.

In diesel engine system design, the PDF of the engine response needs to be

analyzed based on the PDF of different input factors. The relationships between

the factors and responses in engine system design are usually not simple

sum or difference but very nonlinear and complex. Therefore, a numerical

simulation method such as the Monte Carlo simulation with random sampling

is necessary in order to nd out the PDF of the engine response.

Probability distribution selection

There are many complex relationships between different probability

distributions, and they are well developed in the theory of probability and

Diesel-Xin-03.indd 276 5/5/11 11:46:13 AM



277Optimization techniques in diesel engine system design

statistics. There are numerous textbooks and handbooks in this area. Table

A.2 (in the Appendix) is compiled to summarize the probability distribution

functions that are commonly used in diesel engine system design. In the

statistical distributions in Table A.2, a consistent set of symbols are used to

facilitate the reader: x or y denotes the random variable value (real number), a

denotes the location parameter, b denotes the scale parameter, and g denotes

the shape parameter. Note that most distributions and their shapes can be

characterized by two or three parameters. For the basics of probability and

statistics, the reader is referred to Law (2006). The details of probability

distribution functions and their statistical properties are provided by Evans et

al. (2000) and Dodson and Schwab (2006). Examples of various probability

distribution curves can be found at the website of the US National Institute of

Standards and Technology at www.itl.nist.gov/div898/handbook/secton3.

Design for variability and design for reliability make extensive use of

probability distributions. In reliability engineering the distribution is usually

tted with respect to time (i.e., mean time to failure used as the random

variable). The most commonly used distributions in reliability engineering

are Weibull, normal, log-normal, and exponential distributions. On the other

hand, in design for variability the statistical distribution is usually tted with

respect to the scattered values of the system factors or responses (i.e., the

factors or responses used as the random variable).

The guidelines of selecting a probability distribution to t univariate

statistical data are summarized as follows:

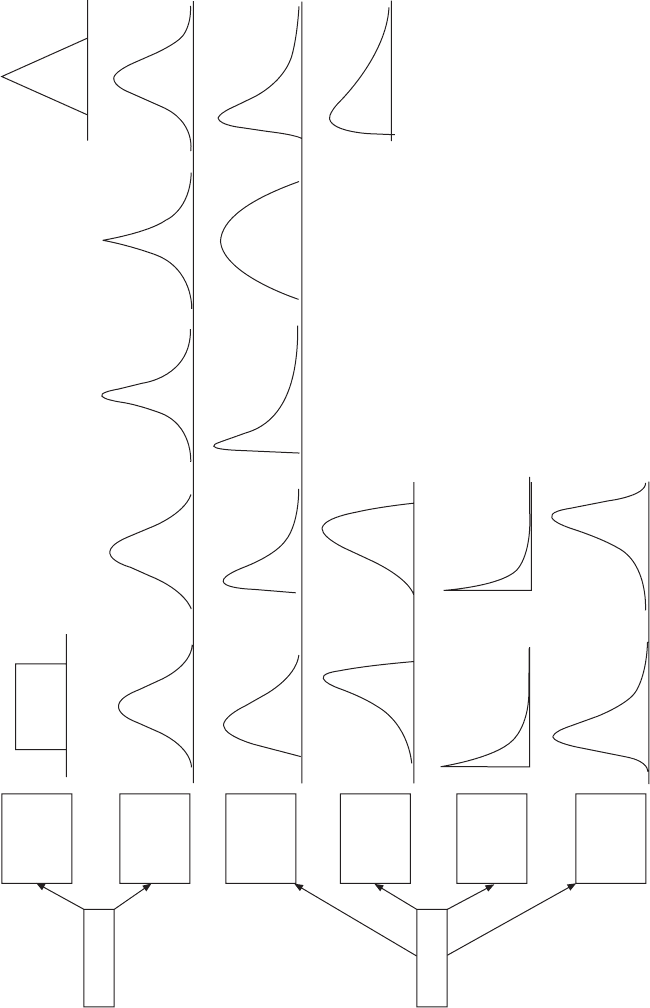
1. It is important to plot and watch the histogram of the actual data to

distinguish the data pattern according to the following aspects and then

select an appropriate type of statistical distribution (Fig. 3.23):

 ∑ continuous distribution vs. discrete distribution

 ∑ symmetric distribution vs. asymmetric distribution

 ∑ clustered around center vs. evenly distributed (i.e., classied by

kurtosis)

 ∑ asymmetric ‘tail’ – outliers skewed positively vs. skewed negatively

or one-side skewed (i.e., classied by skewness)

 ∑ no limits vs. having upper or lower limits (extremes).

2. It is necessary to calculate the statistics of the actual data distribution

(such as mean, standard deviation, skewness and excess kurtosis (see

Table A.1 in the Appendix). Check which distribution function matches

them closely (see Table A.2 in the Appendix).

3. An easy-to-use statistical distribution is an important consideration in

model selection. The selected distribution does not need to be the best-t

distribution for the data, but needs to be a sufciently adequate model

so that the statistical model may yield valid conclusions.

4. When tting the probability data of an engine system response with a

Diesel-Xin-03.indd 277 5/5/11 11:46:13 AM



Symmetric

Asymmetric

Evenly

distributed

Uniform

distribution

Clustered

around

center

Tail or

outliers

positively

skewed

Tail or

outliers

negatively

skewed

One-side-

skewed

(sharp

decaying)

Data have

upper or

lower

limits

Triangular

distribution,

with limits

Normal

distribution

Weibull

distribution

Generalized

log-logistic

distribution

Logistic

distribution

Gamma

distribution

Beta

distribution

Exponential

distribution

Pareto

distribution

Cauchy

distribution

Log-normal

distribution

Laplace

distribution

Beta

distribution

Student’s

t-distribution

Chi-square

distribution

F-distribution

Extreme value

distribution (1),

positively skewed

Extreme value

distribution (2),

negatively skewed

3.23 Selecting continuous probability distribution functions.

Diesel-Xin-03.indd 278 5/5/11 11:46:13 AM



279Optimization techniques in diesel engine system design

selected distribution function, the nature of the relationship between the

response and the factors in the engine processes needs to be considered

in order to judge whether the selected distribution function is reasonable

compared with the probability distribution functions used for the input

factors.

5. The parameters of the selected distribution function for the factors or

responses need to be estimated graphically with probability plotting or

numerically with the methods of maximum likelihood estimation (Dodson

and Schwab, 2006) or least-squares. An analysis of goodness of t can

be conducted to compare the distribution function of the actual data

with that of the tted distribution in order to accept or reject the t. For

details of selection, tting and testing statistical distribution models, the

reader is referred to Shapiro (1990).

Normal distribution and other commonly used distributions

When the true distribution of a variable is not known, a normal distribution

(also known as the Gaussian distribution or the bell curve) is often assumed.

Normal distribution is the most widely used distribution. It is ubiquitous

in nature and statistics because of the well-known central limit theorem:

every variable that can be modeled as a sum of many small independent

variables is approximately normal. In other words, the sum or average of a

large number of random independent variables is approximately normally

distributed, regardless of the distribution of the variables being summed or

averaged. The data in normal distribution have a strong tendency to cluster

on a central value with symmetric deviations to both sides of the central

mean value. The symmetry of deviation results in zero skewness. The low

probability of large deviations from the mean value (i.e., small ‘tail’ size)

gives zero excess kurtosis. The characteristics of the normal distribution are

elaborated by Dodson and Schwab (2006).

In the family of symmetric distributions the shapes and kurtosis are

different (Fig. 3.23). Some of them have a sharper peak and longer or fatter

tails than the normal distribution (i.e., higher kurtosis). For example, the

logistics distribution has a longer tail and higher kurtosis value than the

normal distribution. Some others may have a lower, wider peak and shorter or

thinner tails than the normal distribution (i.e., lower kurtosis). As an extreme

case when the distribution attens out it becomes the uniform distribution.

Some non-symmetric distributions have a peak in the distribution at

low values and a gradual tapering tail toward higher values. These random

variables can be modeled by a log-normal or Gamma distribution. Some

distributions with the ‘cliff’ shape may be best modeled by an exponential

distribution. In the family of positively skewed distributions (e.g., Weibull,

Gamma, log-normal), increasing the shape parameter shifts the peak of the

Diesel-Xin-03.indd 279 5/5/11 11:46:13 AM



280 Diesel engine system design

distribution to the left and the skewness increases. With a very high shape

parameter, the distribution becomes one-side skewed and has a sharp decaying

shape like in the exponential distribution.

When the statistical data are constrained by an upper or lower limit

(e.g., cooler effectiveness limited to less than 100%, engine ow rate or

pressure limited to greater than zero), using some of the above-mentioned

distributions may create problems that unrealistic numbers exceeding the

limits could be generated. Depending on the type of limit (upper only,

lower only, or both), one of the following distributions that are limited

by an upper or lower limit can be used to t the data: uniform, triangular,

positively skewed, negatively skewed, one-side skewed, or extreme value

distributions. An alternative and approximate way is to use the symmetric

clustered-around-center distributions (e.g., normal) to t the data and then

impose the limits to discard any data exceeding the limits. The penalty of

using this method can be small if the tail in the distribution (i.e., the portion

truncated off) is relatively small.

It should be noted that in statistics theory a few distributions are usually

used in statistical inference analysis rather than modeling physical random

variables, such as the chi-square, F- and student’s t-distributions, because

they are derived distributions from other basic distributions.

3.4.3 Introduction to Monte Carlo simulation

Probabilistic models are sometimes titled with the term ‘Monte Carlo’. Monte

Carlo simulation is a modeling tool for uncertainty and it has been used since

the 1940s. Uncertainty cannot be simply replaced by a single average value.

Otherwise, the estimate and design decisions based on that average will be

way off in general. It is the engines at the extremes of the entire population

that determine the success or failure of the design, rather than the nominal

mean of the entire population. Probability distribution is a much more realistic

way of describing uncertainty in variables subject to risk.

In general terms, the Monte Carlo method refers to any technique that

approximates solutions to quantitative problems by statistical sampling.

It is a general class of stochastic approach for analyzing uncertainty

propagation from model input to model output. It uses random sampling

of the probability distribution functions of the model inputs, often with an

independent and random combination of several inputs at the same time,

to produce outputs and estimate the probability distribution of the outputs.

Independent sampling refers to the fact that there is no correlation between

two or more input distributions. The calculation is usually conducted with

several thousand random samples instead of a few discrete scenarios in order

to satisfy the accuracy requirement of the probability evaluation. The term

Monte Carlo was coined in the 1940s in reference to games of chance by

Diesel-Xin-03.indd 280 5/5/11 11:46:13 AM



281Optimization techniques in diesel engine system design

the physicists working on the nuclear weapon projects in the Los Alamos

National Laboratory. Its core idea is to use random samples as inputs to

predict the behavior of a complex system or process.

A Monte Carlo simulation method consists of the following steps:

1. Create a deterministic parametric model linking the input with the output,

Y = f(X

, X

, . . ., X

2. Dene a domain of input factors (number of factors, their sampling

range of variation, and probability distribution).

3. Generate a set of inputs randomly and independently from the domain,

denoted as the ith set of samples, X

, X

, . . ., X

4. Perform a deterministic computation with the model for the ith iteration

to obtain the outputs, Y

, Y

, . . ., Y

, by using the ith set of inputs.

5. Repeat steps 3 and 4 for i = 1 to n (Note: n is the number of

samples).

6. Aggregate the outputs of all individual computations to produce the

probability distributions of the outputs (e.g., histograms or summary

statistics such as frequency of occurrence, minimum, maximum, mean,

median, standard deviation, variance, mean standard error, percentiles,

error bars, tolerance zones, condence intervals, probability or reliability

predictions, skewness and excess kurtosis of the distribution).

Figure 3.10 illustrates the basic principle of the Monte Carlo simulation.

Different types of probability distributions can be used for the inputs, for

example, normal or Gaussian distribution, log-normal distribution, uniform

distribution, exponential distribution, or triangular distribution. The output is

not a single xed value, but a range of possible outcomes with a probability

distribution. The Monte Carlo method is powerful in handling multiple

dimensions of uncertainties (i.e., many input factors). It can also handle

any statistical distribution of random input factors with straightforward

implementation. Good Monte Carlo simulation relies on the quality of random

numbers. As more data points are sampled in the statistical probability

distribution, the results of the Monte Carlo simulation converge to a better

approximation. The large amount of sampling cases required may become

a drawback of the Monte Carlo method when the function evaluation for

each case is computationally expensive. The Monte Carlo method provides

an estimate of the expected value of a random variable and also predicts the

estimation error. The estimation error is given by

3.39

where s is the standard deviation of the random variable, and n is the number

of samples. More in-depth discussions and advanced techniques related to

the Monte Carlo method can be found in Hampson et al. (2002), Zou et al.

Diesel-Xin-03.indd 281 5/5/11 11:46:13 AM



282 Diesel engine system design

(2004), Daniels and Miazgowicz (2007), Donders et al. (2007), Farizal and

Nikolaidis (2007) and Nikolaidis et al. (2008).

By exploring thousands of combinations of the full range of possible

outcomes, using the Monte Carlo simulation may not only obtain more

accurate results in the face of uncertainty but also reveal the sensitivity on

which input has the biggest impact on the probability distribution of the

outputs. The Monte Carlo method expands the engine sensitivity analysis

from the level of deterministic single-point prediction used for design-for-

target to a more advanced level of nondeterministic prediction used for

design-for-reliability to assess the probability of the risks.

3.4.4 Previous research in reliability-based design

optimization

Yan et al. (1993) analyzed the effects of statistical distribution of the

design factors on emissions variability. The design factors included fuel

injector nozzle ow, nozzle protrusion, spray cone angle, piston-to-head

clearance, fuel injection timing and pressure, oil contribution, valve stem

seal leak rate, and swirl ratio. The resulting mean value and the standard

deviation of the emissions were used to set the emissions goal in engineering

development to ensure the entire engine product population could meet the

emissions requirement. A proper emissions deterioration factor was taken into

consideration in dening the engineering emissions margins. They discovered

that the injection timing variability was mainly responsible for NO

and HC

variations, while the variability from nozzle ow, injection pressure/timing

and oil contribution controlled PM variation. Such sensitivity information

could be used to adjust the tolerance of the control factors.

Dave and Hampson (2003) used the Monte Carlo simulation to investigate

the effects of statistical distributions of four factors on the probability

distributions of NO

and BSFC. The four factors were injection timing,

charge air cooler outlet temperature, cylinder wall temperature and intake

valve opening timing. They used the RSM to optimize the mean values

of the four design factors to shift the mean value of NO

and reduce the

standard deviation of NO

so that the mean of NO

was at 3s below an upper

control limit in order to ensure emissions compliance. Meanwhile, BSFC

was minimized for a target failure rate of NO

and BSFC.

Kokkolaras et al. (2005) analyzed the effects of variability on hybrid-

hydraulic truck performance (e.g., fuel economy). The variability included

many random design parameters in the fuel cell, the engine and the vehicle.

The probability density function of the vehicle fuel economy was determined

with a skewed distribution. In RBDO simulation, a large amount of Monte

Carlo simulation was required. They had to use fast surrogate models to

conduct the Monte Carlo simulation. They used a variable screening technique

Diesel-Xin-03.indd 282 5/5/11 11:46:13 AM



283Optimization techniques in diesel engine system design

to identify the most important random factors in order to decrease the size

of the RSM DoE in order to build accurate surrogate models. They came to

the following ndings:

∑ The most important factors for driving cycle fuel economy were fuel

injection timing, vehicle frontal area, rolling resistance, and transmission

efciency.

∑ The most inuential factors for vehicle acceleration performance were fuel

injection timing, vehicle frontal area, intake boost pressure, transmission

efciency and engine compression ratio.

∑ The most important factors for silent watch fuel economy were fuel cell

temperature, humidity ratio, and membrane thickness.

They used RBDO to quantify the trade-offs between fuel economy and

reliability. They found the trade-off was highly nonlinear, and the fuel

economy increased exponentially at very high reliability levels.

Catania et al. (2007) analyzed the variability of fuel consumption caused

by driver driving style, vehicle weight, vehicle resistance, engine BSFC and

transmission efciency. They concluded that the probability distribution

shape of fuel economy does not correlate with the distribution shape of the

input factors.

The application of variability-based design optimization in piston assembly

tribology was carried out by Hoffman et al. (2003), Ejakov et al. (2003) and

Chan et al. (2004).

Rahman and Sun (2003) applied robust design and variability-based

optimization to address the reliability problem of engine cooling system and

the variation of top tank temperature. They assumed a normal distribution for

each input factor in the Monte Carlo simulation. A probability distribution

curve of the top tank temperature was produced and compared with a

prescribed maximum design limit of the temperature. The failure rate was

calculated as the probability of the top tank temperature exceeding the limit.

As a design solution, they changed the mean and the standard deviation of

the input factors in order to move the probability distribution curve of the

top tank temperature to meet the reliability target.

Rahman et al. (2007) used multi-objective robust-RBDO to maximize

the cooling system performance and simultaneously minimize its standard

deviation under the probabilistic reliability constraints. The two objectives

used were the mean performance and its variation. They achieved a balance

(or trade-off) between reliability and robustness by simultaneously optimizing

(maximizing) the mean performance and minimizing the performance

variation. A trade-off occurred because it was impossible to improve one

objective without sacricing the other. The trade-off was computed by using

the concept of Pareto efciency. The Monte Carlo simulation with 10,000

samples was used to determine the statistics of an engine cooling system.

Diesel-Xin-03.indd 283 5/5/11 11:46:13 AM



284 Diesel engine system design

The input random factors included ambient temperature, engine speed, and

heat rejection. The deterministic design control factors included cooling air

ow rate and compressor pulley ratio. Three objectives were used in the

optimization: (1) maximizing the mean of top tank temperature (for good

BSFC); (2) minimizing the standard deviation of top tank temperature (for

robustness); and (3) minimizing the front-end air ow rate (for good BSFC).

By optimizing the control factors and controlling the variation of random

control factors, an optimal balance between reliability and robustness of the

engine cooling system was achieved. The probability of acceptable engine

top tank coolant temperature was increased from 57% to 95%. Meanwhile,

the standard deviation of the top tank temperature was reduced from 17.5∞F

to a much smaller value of 8.2∞F.

3.4.5 Probabilistic simulation in diesel engine system

design

A Monte Carlo simulation is conducted in Tables 3.6 and 3.7 and Figs 3.24–

3.26 to investigate the impact of variability on the probability distributions

of different engine performance parameters for a heavy-duty diesel engine

at the rated power condition. The variability studied includes mainly the

tolerances in engine design and control parameters. There are six cases in

the simulation, corresponding to ve different ambient conditions (Cases

1–5) and one sensitivity case to analyze the effect of exhaust restriction

variation (Case 4S). Case 1 is at sea-level altitude (0 ft.) and 77∞F (25°C)

normal ambient in standard laboratory conditions. Case 2 is at sea-level

altitude and 100∞F (38°C) hot ambient for in-vehicle conditions with an

increased air temperature at the compressor inlet by an amount of rise-over-

ambient (ROA). Case 3 is at sea-level altitude, 122∞F (50°C) hot ambient

and in-vehicle. Case 4 is at 5500 feet (1676 meters) high altitude, 100∞F

(38°C) hot ambient and in-vehicle. Case 5 is at 10,000 feet (3048 meters)

high altitude, 85∞F (29°C) ambient and in-vehicle. Case 4S is the same as

Case 4 except for using a 10% higher exhaust restriction ow coefcient

that simulates a less restrictive aftertreatment system such as a clean DPF

after soot regeneration. The standard deviation of the exhaust restriction

ow coefcient of Case 4S is the same as that in Case 4. Table 3.6 shows

the probability input data used in Case 4. There are in total 17 random input

factors, all assumed in the normal distribution. Basically, the same coefcients

of variation (i.e., the ratio of standard deviation to mean of the samples)

are used for the other ve cases. When the turbine wastegate is fully closed

(as in Case 5), the standard deviation of the wastegate opening is assumed

to be zero. The engine performance results are obtained with GT-POWER

simulation for each sample of the Monte Carlo simulation.

Figure 3.24 shows the probability distributions of some input factors.

Diesel-Xin-03.indd 284 5/5/11 11:46:14 AM



Table 3.6 Input data of Case 4 used in Monte Carlo simulation for probabilistic engine system design (an example at the rated fueling, 5500

feet high altitude and 100°F ambient temperature)

Input

factor

code

Parameter name Unit Type of

factors

Baseline

Mean

Baseline

standard

deviation

Coefﬁcient

of variation

Statistical distribution

assumed in the model

Engine compression ratio – Random 16 0.2 1.25% Normal distribution

HP turbine wastegate opening mm Random 4.68462 0.140539 3.00% Normal distribution

EGR valve opening (ﬂow coefﬁcient) – Random 0.128757 0.001289 1.00% Normal distribution

Fuel mass ﬂow rate Random Baseline 0.5% Normal distribution

Exhaust restriction ﬂow coefﬁcient – Random 0.39 0.02 5.13% Normal distribution

HP compressor efﬁciency multiplier – Random 1 0.013 1.30% Normal distribution

LP compressor efﬁciency multiplier – Random 1 0.013 1.30% Normal distribution

HP turbine efﬁciency multiplier – Random 0.95 0.013 1.37% Normal distribution

LP turbine efﬁciency multiplier – Random 0.95 0.013 1.37% Normal distribution

Normalized HP turbine area (mass multiplier) – Random 1.1 0.01 0.91% Normal distribution

Normalized LP turbine area (mass multiplier) – Random 1 0.01 1.00% Normal distribution

Start-of-combustion timing degree Random –10 0.1 1.00% Normal distribution

Inter-stage cooler coolant inlet temperature

∞F

Random 147.9 2 1.35% Normal distribution

EGR cooler coolant inlet temperature

∞F

Random 206.5 2 0.97% Normal distribution

Engine coolant inlet temperature

∞F

Random 216.8 2 0.92% Normal distribution

Charge air cooler cooling air inlet temperature

∞F

Random 113 2 1.77% Normal distribution

LP-stage compressor inlet air temperature

AMB

+DT

ROA

)

∞F

Random 115 3 2.61% Normal distribution

Notes:

The coefﬁcient of variation is calculated as the ratio of standard deviation to mean. (1)

X(2)

and X

are only applicable for in-vehicle conditions rather than the standard lab engine condition at sea level (0 ft. altitude) 77∞F

ambient.

In the case of sensitivity analysis on the effect of exhaust restriction variation, the mean value of the exhaust restriction ﬂow coefﬁcient is (3)

increased by 10% from the baseline mean 0.39 to 0.429.

Diesel-Xin-03.indd 285 5/5/11 11:46:14 AM

