Xin Q. Diesel Engine System Design

226 Diesel engine system design

∑ Step 2 – minimum- or maximum-contour optimization for the second

objective (Fig. 3.8b). The method continues by conducting another

constrained single-objective optimization to maximize the exhaust

temperature in the entire emissions domain. The DoE factors form

the same boundary mapped in this domain. It should be noted that the

maximum exhaust temperature point C, subject to the same emissions

constraints as for point A, has a higher BSFC than point A.

∑ Step 3 – multiple Pareto-optimal curves at different constraints (Fig.

3.8c). The two extreme points (A and C) of the Pareto-optimal curve

have been determined for a selected emissions level. Point B can be

generated by running a similar optimization as in Step 2 to maximize

the exhaust temperature while subject to a constraint at a certain BSFC

level that is selected between the BSFC of point A and the BSFC of

point C. Then, the Pareto curve can be constructed by linking points A,

B, and C to display the trade-off. It should be noted that the dotted curve

linking point A directly to point C is not a part of the Pareto optimal

front because the points along the dotted curve are not optimized in any

sense. Another Pareto-optimal curve at another emissions level A¢–B¢–C¢

can be obtained similarly. On these Pareto-optimal points, the values of

another objective function (e.g., the system cost) can be calculated and

marked on the chart to form certain constant-value contours. It is noted

that the system cost may reach a minimum along the Pareto-optimal

curve. A nal optimum solution can be selected from this chart.

Such a chart consisting of multiple Pareto-optimal curves is very convenient

and powerful for selecting the nal optimal solution in diesel engine system

design. The chart is featured by two objectives (BSFC vs. exhaust temperature

here, placed on the horizontal and vertical axes of the chart, respectively)

at several levels of constraints (emissions here) with the values of a third

objective (cost here) marked on the Pareto-optimal curves. The nal design

decision can be made based on such a concise summary of ‘four dimensions’

of information (i.e., three objectives of response/output plus one constraint)

that are distilled from many more dimensions of DoE input factors.

Other optimization methods such as desirability functions are introduced

in Edwards et al. (2000) and Myers and Montgomery (2002).

3.1.9 Optimization in design for target, design for

variability, and design for reliability

Diesel engine system design requires an optimized specication of both

nominal target value and tolerance. Steady-state engine optimization with

a large number of factors usually requires a DoE technique. Figure 3.9

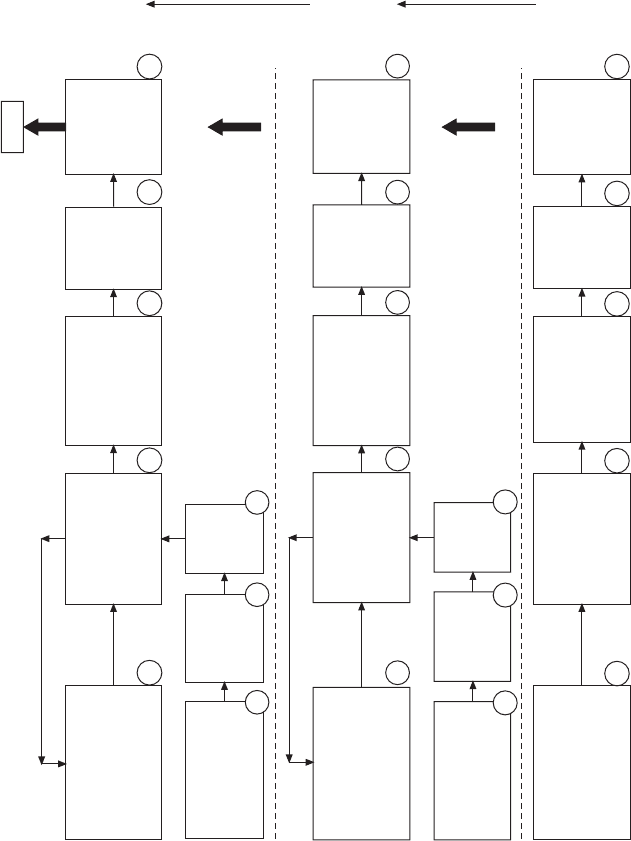
illustrates the processes of the optimization for diesel engine system design.

The processes consist of three layers of work:

Diesel-Xin-03.indd 226 5/5/11 11:45:55 AM



Iterate for all cases in DoE-2 Optimal for reliability

Select factors & levels:

• Control factors (for

nominal & tolerance)

• noise factors (for

reliability probability

distribution)

Run Monte Carlo

simulation with

system models or

RSM-1 models,

output responses &

reliability statistics

Build DoE-2 RSM-2

emulator models

using factor levels

and probability

characteristic

responses/statistics

Optimize

to choose

nominal

values and

tolerances

Conduct

conﬁrmation

runs

Select factors, setup

ranges and levels:

• Control factors

• All noise factors

Select factors, setup

ranges and levels:

• Control factors

• All noise factors

Select factors & levels:

• Control factors (for

nominal & tolerance)

• Noise factors (for

variability probability

distribution)

Run Monte Carlo

simulation with

system models or

RSM-1 models,

output responses &

reliability statistics

Build DoE-2 RSM-2

emulator models

using factor levels

and probability

characteristic

responses/statistics

Build DoE-1

RSM-1 emulator

models using

factor levels and

responses

Optimize

to choose

nominal

values and

tolerances

Optimize

to choose

nominal

values

Conduct

conﬁrmation

runs

Conduct

conﬁrmation

runs

Run reliability

models

to obtain

responses

Run system

models

to obtain

responses

Select factors, set up

ranges and levels:

• Control factors

• Noise factors

Build

DoE-1

RSM-1

emulator

models

Build

DoE-1

RSM-1

emulator

models

End

(Optional)

Run system models

to obtain responses

Optimal for variability

Preliminary sub-optimal

Iterate for all cases in DoE-2

Design for

reliability

(nondeterministic)

Design for

variability

(nondeterministic)

Design

for target

(deterministic)

3.4 3.5 3.6 3.7 3.8

3.1

2.4

2.5 2.6 2.7 2.8

2.1

2.2 2.3

1.1

1.2

1.3

1.4

1.5

3.2 3.3

3.9 DoE optimization process for steady-state diesel engine system design.

Diesel-Xin-03.indd 227 5/5/11 11:45:55 AM



228 Diesel engine system design

∑ a deterministic ‘design for target’ process to screen for preliminary sub-

optimal of the nominal value of the design specication

∑ a nondeterministic ‘design for variability’ process to reach the optimal

design – both nominal value and tolerance of the design specication,

subject to variability

∑ a nondeterministic ‘design for reliability’ process to reach the optimal

design – both nominal value and tolerance of the design specication,

subject to reliability.

The difference between variability and reliability is that reliability analysis

includes the effect of the time-dependent noise factors (e.g., deterioration).

The design for variability uses probabilistic objective functions to control both

nominal value and tolerance range in order to make the design insensitive

to noise factors.

The contents in steps 1.1–1.5 described in Fig. 3.9 for the layer of design

for target are explained in detail in Section 3.2. The RSM-1 model mentioned

in step 1.3 refers to the surface-t emulator model that relates the nominal

value of the response to factors. There is no emulator model for the tolerance

in this layer.

The optimization in design for variability is illustrated in steps 2.4–2.5

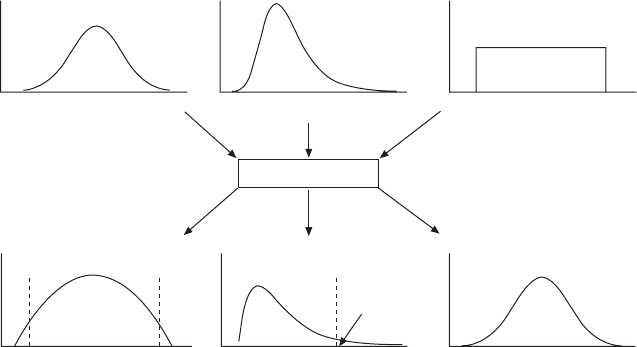
in Fig. 3.9. The associated Monte Carlo simulation is shown in Fig. 3.10.

Basically, the Monte Carlo simulation is a probability calculation by using

random combinations of random samples selected from the probabilistic

distributions of several input factors. The probabilistic distribution of the

output response can be predicted along with an estimation of the failure

rate or reliability. To make the estimation accurate, the amount of random

Normal distribution Extreme value

distribution

Uniform

distribution

X

1

Y

1

X

2

Y

2

X

3

Y

3

Model Y = f (x)

Beta distribution Gamma distribution Normal distribution

Reliability

= 90%

3.10 Statistical uncertainty propagation and design for variability.

Diesel-Xin-03.indd 228 5/5/11 11:45:56 AM



229Optimization techniques in diesel engine system design

samples needs to be very large. The details of the Monte Carlo simulation

are provided in Section 3.4.

The noise factors mentioned in step 2.1 in Fig. 3.9 refer to all the noise

factors covered by the variability analysis. The steps 2.1–2.3 compose

DoE-1, and they are similar to steps 1.1–1.3 in nature. The level setting of

the noise factors in step 2.1 is handled in the same manner as in step 1.1

(i.e., only for levels of mean values). The DoE-1 RSM-1 emulator surface-t

models are often needed as surrogate models to replace the computationally

intensive engine cycle simulation models because the Monte Carlo simulation

in step 2.5 requires thousands of runs. The thousands of Monte Carlo runs

need to be iterated for each case in DoE-2. It should be noted that the level

setting of the noise factors in the DoE-2 in step 2.4 is different from that in

step 2.1 (or step 1.1). The noise factors in step 2.4 need to be described by

several distribution factors (e.g., mean, standard deviation; scale parameter

and shape parameter) to reect its particular probabilistic distribution shape.

These factors are called probability distribution factors. Each probability

distribution factor is a factor in DoE-2. Each noise factor in step 2.4 needs

to have several factor levels for each probability distribution factor within

a reasonable range for the shape of the given type of probability function.

For example, for a noise factor of turbine efciency, its ‘mean value’ factor

needs to have ve levels of setting to cover a range of possible mean values

of the probabilistic distribution of the turbine efciency, for example at

58%, 59%, 60%, 61%, and 62%. Its ‘standard deviation’ factor also needs

to have ve levels of setting to cover a range of possible different shapes of

the probabilistic distribution of the turbine efciency, for example at 0.3%,

0.6%, 0.9%, 1.2%, and 1.5%. Obviously, the DoE size in step 2.4 is usually

larger than that in step 2.1. For example, assuming the DoE-2 in step 2.4

has 10 factors (i.e., 4 control factors, and 3 noise factors which give 6 noise

probability distribution factors) and 210 cases (runs), for each case the Monte

Carlo simulation needs to be executed 1000 times by taking 1000 random

probability sample combinations. Such a huge amount of computation usually

cannot be handled by using the original detailed system models. Therefore,

the RSM-1 model described in step 2.3 is needed here as the fast surrogate

model.

The output of step 2.5 in Fig. 3.9 includes all the engine responses in

the form of probabilistic distribution shapes, their statistical properties for

a selected t of probability distribution function, and probability statistics

(i.e., failure rate for variability). The statistical properties of the responses

may include the following: minimum, maximum, mean, standard deviation,

skewness, excess kurtosis, and mode. (For the denition of these probability

distribution parameters, see Tables A.1 and A.2 in the Appendix.) Suspected

outliers in the probability distribution of the simulated responses are not

uncommon. Outliers are not necessarily bad data points. They should be

Diesel-Xin-03.indd 229 5/5/11 11:45:56 AM



230 Diesel engine system design

handled carefully instead of simply being removed automatically. The

RSM-2 emulator models are described in step 2.6 by linking the factors of

DoE-2 to the probability distribution responses and probability statistics.

The emulator models allow an evaluation of the sensitivity of the output’s

probability distributions to all the input factors by using the analysis techniques

introduced earlier (e.g., parametric sweeping, two-dimensional optimization

with contour maps).

Step 2.7 is critical in robust optimization. In the traditional theory of robust

design, Dr Taguchi used a ‘two-step optimization’ approach (Fowlkes and

Creveling, 1995). In this approach, the product’s tolerance is rst reduced

to a desirable probability distribution shape, then, the entire probability

distribution curve is shifted to the desirable target by adjusting the nominal

design value. Such a two-step approach has certain disadvantages. For

example, the nominal target design and tolerance design are separated and their

interactions are difcult to be handled efciently. In the robust optimization

theory for diesel engine system design here, those disadvantages are overcome

by using a one-step simultaneous optimization of both nominal design and

tolerance design. The mathematical formulation of the optimization by using

the DoE-2 RSM-2 emulator models in step 2.7 enables such a simultaneous

optimization because the models include all the statistical properties (nominal

or mean, tolerance or deviation) for constrained optimization (e.g., subject to

a constraint of failure rate at or less than certain prescribed target value). It

should be noted that such an advantage of the proposed ‘design for variability’

approach over the traditional ‘two-step optimization’ approach can only be

achieved by introducing the RSM into the robust design area.

The last layer of the system optimization is design for reliability. It is similar

to the design for variability (Fig. 3.9), but still different. The reliability-related

system models, probability distributions, and output statistics should be used

in steps 3.2, 3.4, and 3.5 shown in Fig. 3.9, respectively. As a comparison,

the variability-related items should be used in steps 2.2, 2.4, and 2.5.

3.2 Response surface methodology (RSM)

Response surface methodology (RSM) is a DoE approach in which the output

variables are called ‘responses’ and the independent input variables are called

‘factors’. The response function forms a surface or hyper-surface (if there

are more than two factors) in the factor space. Optimization is conducted

to search for a global optimal point (minimum or maximum) on a surface

dened by the objective function. Detailed discussions on RSM are provided

by Eriksson et al. (1999) and Myers and Montgomery (2002). A brief overview

of the most important concepts and procedures in the RSM theory related to

diesel engine system design is summarized in this section.

Diesel-Xin-03.indd 230 5/5/11 11:45:56 AM



231Optimization techniques in diesel engine system design

3.2.1 Overview of the RSM process

Engine optimization requires a continuous quantitative mathematical model

to link the factors to responses (either steady state or transient) and solve

for global optima. In engine applications the relationship between the design

or operating factors and the responses is highly nonlinear and complex. For

example, the impact of turbine area and EGR valve opening on air ow

rate is governed by a large nonlinear system of equations of the engine in-

cylinder cycle process, engine gas ow network, and turbocharging. The

underlying mechanisms are so complex that they cannot be condensed to

‘one equation’ that still reects the physical laws and can be used as the

objective or constraint function. Moreover, sometimes the true functional

relationships or physical models are not even understood or available, and

the governing equations of the processes are simply lacking. The engineer

must approximate the underlying processes with an appropriate empirical

model in the form of:

Y

obs

= Y + u = f(X

1

, X

2

, . . ., X

k

) + u 3.11

which links the input factors X

i

to an approximation (Y) of the observed

output response Y

obs

. It should be noted that the terms in the empirical model

usually do not contain any physical meaning. Here u is an error term that

reects the sum of experimental errors and the ‘lack-of-t’ model errors not

accounted for in the function f. The experimental errors are usually assumed

to have a normal distribution with a mean at zero and a constant variance.

In the RSM, such a model is built with the linear regression technique by

tting a set of sample data to minimize the errors. Although more complicated

mathematical functions (e.g., spatial stochastic process models or sophisticated

weighted linear interpolation models, neural network, radial basis function

network, and spline-cubic function) may be used to t the data, polynomial

models are most widely used to approximate the true functions. Usually, for

a RSM problem with multiple input factors the function f is a rst-, second-

or third-order polynomial. Such an empirical model is called a response

surface model or surface-t emulator.

The RSM optimization process usually consists of the following six

steps:

1. Prepare factors and their levels in a statistical DoE design matrix.

2. Generate responses by either experimental testing or numerical simulation

(for instance, using the engine cycle simulation software to produce

performance output data).

3. Build emulators to link the factors and the responses by using polynomials

or other continuous functions with surface t.

4. Validate the emulator models by checking the surface-t accuracy with

spare runs (i.e., use the DoE runs that are not used during emulator

model building to test the accuracy of model prediction).

Diesel-Xin-03.indd 231 5/5/11 11:45:56 AM



232 Diesel engine system design

5. Conduct optimization by using the emulator and advanced searching

algorithms to search for the global optima under given constraints.

6. Produce con rmation runs for the optimum result.

3.2.2 Building emulator models

Appropriate statistical DoE design is dependent upon the model structure of

the emulator. Unlike the curve  t for a response with respect to only a single

factor where a polynomial of very high order (e.g., 6th order) can be used, a

lower-order polynomial (usually less than 3rd) is generally used in RSM to

handle multiple factors. For a complex process, lower order or fewer terms

in the polynomial model generally makes the model deviate more from the

true physical mechanism, but allows fewer DoE runs to build the model.

For a simple linear system without interactions, a  rst-order polynomial

model, also called main effect model, can be used. It is given by

YY

CC

X

obs

YY

obs

YY

i

k

ii

YY =YY

YY YY

+

=1

uu

+

uu

+

uu

CC

uu

CC

X

uu

X

ii

uu

ii

X

ii

X

uu

X

ii

X

uu

CC CC

uu

CC CC

CC+ CC

uu

CC+ CC

uu

CC CC

uu

CC CC

ii

uu

ii

X

ii

X X

ii

X

uu

X

ii

X X

ii

X

uu

=

uu

=

uu

0

CC

uu

CC

0

CC

uu

CC

CC CC

uu

CC CC

0

CC CC

uu

CC CC

S

CCSCC

CC

uu

CCSCC

uu

CC

Ê

uu

Ê

uu

Ë

uu

Ë

uu

Ë

uu

Á

uu

Ê

Á

Ê

uu

Ê

uu

Á

uu

Ê

uu

Ë

Á

Ë

uu

Ë

uu

Á

uu

Ë

uu

Ë

uu

Á

uu

Ë

uu

ˆ

uu

ˆ

uu

¯

uu

¯

uu

¯

uu

˜

uu

ˆ

˜

ˆ

uu

ˆ

uu

˜

uu

ˆ

uu

¯

˜

¯

uu

¯

uu

˜

uu

¯

uu

¯

uu

˜

uu

¯

uu

3.12

where Y

obs

is the observation values of the DoE test run, and Y is the  tted

value by the polynomial model. If there is a ‘curvature’ on the surface of the

response function, interaction terms or a higher-order polynomial must be

used to model the ‘curvature’ in such a more complex system. For example,

a linear-with-interaction model is given by

YY

CC

obs

YY

obs

YY

i

k

ii

j

k

j

YY =YY

YY YY

+

=

CC CC

CC+ CC

=1

ii=1ii

,<

ii,<ii

j,<j

1

=2

u

CC

0

CC

0

CC

0

CC

CC CC

0

CC CC

SS

CCSSCC

XSSX

ii

SS

ii

X

ii

XSSX

ii

X

+SS +

S

–

kkk

ij

CX

ij

CX

ij

CX

ij

CX

ij

X

ij

X

ij

CX CX

ij

CX

ij

CX

ij

X

ij

X

ij

+

Ê

Ë

Á

Ê

Á

Ê

Ë

Á

Ë

Á

Ë

ˆ

¯

˜

ˆ

˜

ˆ

¯

˜

¯

˜

¯

u

3.13

where X

i

X

j

is the interaction term. Another example is a second-order

(quadratic) model, which is a second-order Taylor series approximation:

YY

CC

XC

X

obs

YY

obs

YY

i

k

ii

XC

ii

XC

i

k

ii

i

YY =YY

YY YY

+

=

CC CC

CC+ CC

=1

2

u

CC

0

CC

0

CC

0

CC

CC CC

0

CC CC

SS

CCSSCC

XCSSXC

ii

SS

ii

XC

ii

XCSSXC

ii

XC

XC +XCSSXC +XC

+

=1

,<

1

=2

SS

ii

=1ii=1

,<ii,<

j

,<j,<

k

j

k

ij

CX

ij

CX

ij

CX

ij

X

ij

X

ij

–

Ê

Ë

Á

Ê

Á

Ê

Ë

Á

Ë

Á

Ë

ˆ

¯

˜

ˆ

˜

ˆ

¯

˜

¯

˜

¯

u

3.14

Note that equations 3.12–3.14 contain p terms of polynomial or regression

coef cients, where

pk

p

pk = 1 +pk

=

fo

r

fi

rs

t-

or

de

r

w

ithout inter

actio

ithout interactioithout inter

n

1 +

(

–

)

fo

r

fi

rs

t-

or

de

r

w

ith inter

a

ith interaith inter

kk

+ kk+

k

12

)12)

/

12/12

ctio

cctioc

n

fo

r

s

econd-

or

de

r

+

(

1)

pk

= 1 + 2pk = 1 + 2

kk

(kk (

–/

1)–/ 1)

2

w

ith inter

actio

ith interactioith inter

n

Ï

Ì

Ô

Ï

Ô

Ï

Ì

Ô

Ì

Ó

Ô

Ì

Ô

Ì

Ó

Ô

Ó

3.15

and k is the number of factors. One advantage of using polynomial in the

Diesel-Xin-03.indd 232 5/5/11 11:45:57 AM



233Optimization techniques in diesel engine system design

emulator is that the polynomials are everywhere differentiable so that the

derivative-based optimization algorithms can be used to search for the optima.

A second-order model requires more DoE runs and also more factor levels

to construct than a rst-order model.

A rst-order model of Y = C

0

+ C

1

X

1

shows a straight line in the domain

of response vs. factor (Y vs. X

1

). A rst-order model of Y = C

0

+ C

1

X

1

+

C

2

X

2

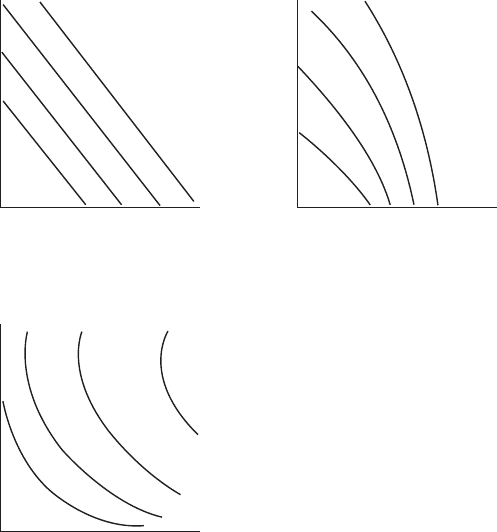
without interactions gives a tilted plane in the three-dimensional space

domain of response vs. factor (Y vs. X

1

and X

2

). It is reected as a contour

map in the two-dimensional domain of X

1

vs. X

2

for the response that has

parallel straight lines with constant intervals (Fig. 3.11a). A higher-order

model including the interaction terms is characterized by the non-parallel

variable-interval contours (Fig. 3.11b and Fig. 3.11c), or the shapes of

stationary ridges, rising ridges, mountains or saddle surfaces if viewed in a

three-dimensional space (Fig. 3.12).

Second-order polynomials have been widely used because they offer a good

compromise between model exibility and DoE size. Usually a second-order

Factor X

2

Factor X

2

Factor X

2

Y = 10

20

30

40

Factor X

1

Factor X

1

Factor X

1

(a) First-order model

without interaction

(c) Second-order model

with interaction

(b) First-order model with

interaction

3.11 Interaction effects.

Diesel-Xin-03.indd 233 5/5/11 11:45:57 AM



(a) Simple maximum

(b) Stationary ridge

(c) Rising ridge (d) Col, saddle, or minimax

76

80

92

84

76

68

84

82

76

80

76

82

84

72

76

80

81

80

76

72

x

1

x

2

x

2

x

2

x

1

x

1

x

1

x

1

3

h = 80 + 4x

1

+ 8x

2

– 4x

1

2

– 12x

2

– 12x

1

x

2

h = 80 – 4x

1

+ 12x

2

– 3x

1

2

– 12x

2

– 12x

1

x

2

h = 80 + 4x

1

+ 8x

2

– 3x

1

2

– 12x

2

– 12x

1

x

2

h = 80 + 4x

1

+ 8x

2

– 2x

1

2

– 12x

2

– 12x

1

x

2

3.12 Some examples of types of surfaces deﬁned by the second-order model in two variables x

1

and x

2

(from Box and

Draper, 1987; also adapted by Myers and Montgomery, 2002).

Diesel-Xin-03.indd 234 5/5/11 11:45:58 AM



235Optimization techniques in diesel engine system design

model is necessary and suf cient to approximate the true response surface

in most applications of engine system design except for some extremely

nonlinear scenarios (e.g., soot sensitivity, very complex interactions among

the factors, or very large range of the DoE factors). In these cases, a third-

order model becomes necessary. For example, the cubic terms

X

i

3

and the

interaction terms

XX

ij

XX

ij

XX

2

XX

2

XX

or X

i

X

j

X

u

need to be used for a highly nonlinear

exhaust restriction  ow coef cient, EGR circuit restriction  ow coef cient,

or VGT vane opening, also taking their interactions with other factors into

account (Figs 3.13 and 3.14).

Polynomial models are ‘parametric’ models which provide the regression

coef cients to represent the model structure and individual factor effects. In

statistics, the regression coef cients are called ‘parameters’. Non-parametric

or non-polynomial models cannot output such descriptions of the model

structure or the model coef cients. The non-parametric models include spatial

stochastic process models, radial basis function, and neural network. They

offer  exibility to adapt to the characteristics of highly nonlinear responses

or to build accurate models in the presence of noisy or uncertain experimental

or simulation data. The validity of higher-order polynomial models compared

to other non-polynomial models has been proved by Bates et al. (2000). The

details of stochastic process models are explained by Edwards et al. (2000).

Neural network models are discussed by Shayler et al. (2000) and He and

Rutland (2004).

Although sometimes it cannot match over the entire factor space, a

polynomial model usually can approximate the true functional relationship

quite well for a relatively small region. Assuming the number of DoE runs

is n for each response parameter shown in equation 3.14, the sum of the

squares of the errors of all n runs is given by:

S

SS

S

r

n

r

n

obs

r

i

k

ii

r

i

YC

SSYCSS

obs

YC

obs

SS

obs

SSYCSS

obs

SS

r

YC

r

SS

r

SSYCSS

r

SS

CX

ii

CX

ii

=1

2

=1

,

=1

,

=1

=

SSYCSS – SSYCSS

–

u

0

SS

0

SS

SS-SS

kkk

ii

ir

ii

j

k

j

k

ij

ir

jr

CX

ii

CX

ii

CX

ij

CX

ij

X

,

ir,ir

–

2

=1

ii=1ii

,<

ii,<ii

j,<j

1

=2

,,

ir,,ir

jr,,jr

2

–

SS

Ê

SS

Ê

SS

Ë

SS

Ë

SS

Á

SS

Ê

SS

Á

SS

Ê

SS

Ë

Á

Ë

SS

Ë

SS

Á

SS

Ë

SS

ˆ

¯

˜

ˆ

˜

ˆ

¯

˜

¯

3.16

The method of least-squares is used to solve for the regression coef cients

in the polynomial model by minimizing

S

r

n

r

=1

2

u

. The model parameters or

regression coef cients C

i

, C

ii

and C

ij

, i, j = 1, . . . k, in equations 3.12–3.14 are

solved by multiple linear regression analysis with the method of least-squares

(also called surface  t). The coef cients are affected by the experimental

design of the DoE matrix that is used to collect the data. The difference

between the observation value Y

obs

and the  tted value Y is called residual.

The details of the mathematical solution of least-squares and analysis of

variance (ANOVA) are provided by Eriksson et al. (1999) and Myers and

Diesel-Xin-03.indd 235 5/5/11 11:45:59 AM



Xin Q. Diesel Engine System Design

Подождите немного. Документ загружается.