Xin Q. Diesel Engine System Design
Подождите немного. Документ загружается.

216 Diesel engine system design
© Woodhead Publishing Limited, 2011
6. identifying the optimum factor levels;
7. predicting the optimum responses by using a signal-to-noise ratio and
condence interval;
8. checking the predicted optimum against design constraints; and
9. conducting the conrmation run.
It should be noted that Taguchi’s signal-to-noise ratio method does not
always give the best results, especially when the objective is to achieve a
target response rather than to minimize or maximize the response. As pointed
out by Myers and Montgomery (2002), maximizing a signal-to-noise ratio
does not distinguish which control factors are the location effects (affecting
the mean) and which are the dispersion effects (affecting the variance). In
other words, the signal-to-noise ratios confound the location effect and the
dispersion effect so that they are not necessarily unique and probably should
not be used as an optimization parameter. Taguchi’s signal-to-noise ratios
were criticized by some statisticians and its utility seems questionable. In
Global mean
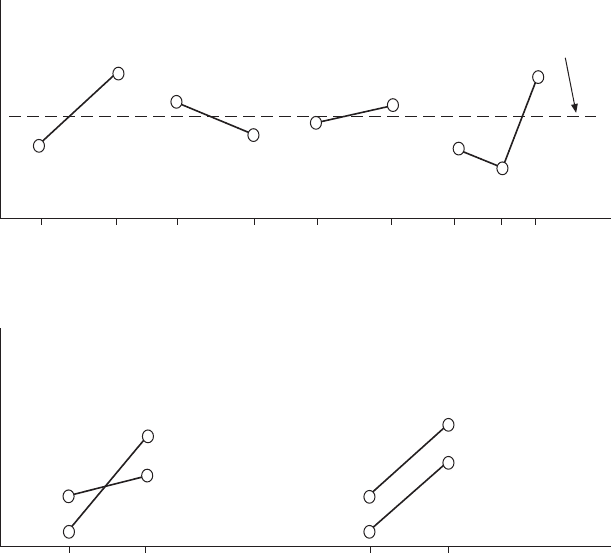
Main-effect plot of DoE data in first-order or linear model (e.g., in Taguchi
method) Note: Three factor levels can also be used
Average responseResponse
–1 +1 –1 +1 –1 +1 –1 0 +1
Factor X
1
Factor X
2
Factor X
3
Factor X
4
–1 +1
Factor X
1
–1 +1
Factor X
1
There is an interaction (i.e., term
X
1
X
2
in emulator model)
Interaction effect plot of DoE data
There is no interaction
Level 2 of factor X
2
Level 1 of factor X
2
Level 1 of factor X
3
Level 2 of factor X
3
3.5 Main effect and interaction plots.
Diesel-Xin-03.indd 216 5/5/11 11:45:52 AM
217Optimization techniques in diesel engine system design
© Woodhead Publishing Limited, 2011
fact, a robust design can be achieved by using RSM to optimize the response
and reduce the variability due to noise factors, without using a signal-to-noise
ratio.
The Taguchi method can work well for determining a robust design if
the interaction effect between control factors is not important (Myers and
Montgomery, 2002). The method provides abundant information about the
interaction between the control factors and the noise factors due to crossed
inner and outer arrays, but the method provides only little information about
the interaction between the control factors or the interaction between the noise
factors because the orthogonal arrays are heavily fractionated. The Taguchi
method offers a quick and simple approach during product optimization
and robust design in order to identify which factor contributes the most,
the optimal factor level, or the impact of noise. However, it seems several
weaknesses exist in the Taguchi method. First of all, the Taguchi method
does not have an empirical surface-t model which includes the higher-
order or interaction effects. Second, Taguchi arrays usually only allow for
two or three levels for each factor, and the preparation of orthogonal arrays
for more levels is not convenient or economical. These make the Taguchi
method not sufciently accurate or convenient for engine system design
applications. Third, only the main effects are emphasized in the Taguchi
method, and the interaction effects of control or noise factors are not given
enough attention in the DoE design arrays, especially the interaction effects
between the control factors. Fourth, the usefulness of optimizing the signal-
to-noise ratios seems questionable. Finally, the way that the noise factors are
handled in an outer array is not efcient in minimizing the number of DoE
runs because the entire main (inner) array needs to be repeated at each run
of the outer array.
The Taguchi DoE method was introduced in detail by Roy (1990), Carey
(1992), Fowlkes and Creveling (1995) and Goh (1994), and will not be
elaborated in this book. In general, although the Taguchi DoE method can
be used in engine system design, its use is usually restricted to preliminary
concept screening or qualitative evaluation (e.g., by using the main effect
plot). For precise system design the response surface methodology with
surface-t formula is much more powerful.
3.1.6 Response surface methodology (RSM)
As introduced earlier, optimization usually requires objective functions and
constraint functions that are continuous mathematical functions relating the
DoE input factors to output responses. The response functions (emulators) are
constructed by the surface-t techniques using least-squares regression to t
the DoE runs. The emulator model consists of the coefcients reecting the
inuence of the factors. The usefulness of the emulator functions in terms
Diesel-Xin-03.indd 217 5/5/11 11:45:52 AM

218 Diesel engine system design
© Woodhead Publishing Limited, 2011
of predicting the main effect and the interaction effect of the DoE factors
and the accuracy of the functions are determined by the structure of the
emulators (i.e., the terms constructed into the emulators) and the statistical
design of the DoE matrix. Response surface methodology (RSM) is an
advanced DoE method that systematically addresses the statistical design
and data processing techniques of DoE.
The emulator model in RSM is usually a polynomial function containing
the terms of the input factors up to third order and the interaction terms,
e.g.,
YC
CX
CX
CX
11
YC
11
YC
CX
11
CX
11
CX
11
CX
12
CX
12
CX
1
2
13
CX
13
CX
1
3
YC =YC
YC
11
YC =YC
11
YC
11
11
YC
11
YC YC
11
YC
+
11
+
11
+
CX CX
CX
12
CX CX
12
CX
1
1
+
+
0
11011
0
11011
11
11011
11
+
+
+
21
22
+
22
+
22
22
22
2
23
2
3
31
CX
21
CX
21
CX
CX
22
CX
22
22
CX
22
22
CX
22
22
CX
22
CX
23
CX
23
CX
31
CX
31
XC
CXXCCX
XC
X
CX
X
33
XC
33
XC
23
XC
23
XC
2
XC
2
XC
33
3
3
1121
CX
1121
CX
12
X
12
X
XC +XC
XC
33
XC +XC
33
XC
XC XC
33
33
XC
33
XC XC
33
XC
23
23
XC
23
XC XC
23
XC
XC+ XC
+
+
1131
32
3
CX
1131
CX
1131
XC
+XC +
32
XC
32
+
32
+XC +
32
+
XX
32
XX
32
1
32213132
3.6
where Y
1
is a response and X
1
, X
2
and X
3
are the factors. Both the control
factors and the noise factors can be mixed together in the RSM DoE design.
The coef cients C
i
are determined with least-squares t. RSM is a better and
more formal method than the Taguchi method for solving DoE optimization
and robust design problems. The comparison between the Taguchi method
and RSM is given in Table 3.2. Detailed discussions about the DoE statistical
matrix design and the data processing techniques of RSM are provided in
Table 3.2 Comparison between Taguchi method and response surface methodology
The Taguchi method Response surface methodology (RSM)
Statistical
DoE
design
Crossed orthogonal arrays ∑
of fractional factorial design
with control factors in inner
array and noise factors in
outer array
Primarily used to screen ∑
factors
Control factors and noise factors ∑
are mixed in more economical DoE
designs with fewer runs
Both linear and higher-order ∑
analysis
Primarily used for both screening ∑
and regression modeling
Graphical
display
Main effect plot, interaction
plot
Contour plot for main and interaction
effects
Analytical
evaluation
Not easy to handle ∑
interaction effects
Analysis of variance ∑
(ANOVA)
Signal-to-noise ratio ∑
analysis
Easy to handle interaction ∑
Surface-fi t emulator regression ∑
models (fi rst-, second- and third-
order) including interaction terms
built with least squares
Analysis of variance (ANOVA) for ∑
regression models
Canonical analysis ∑
Ridge analysis ∑
Diesel-Xin-03.indd 218 5/5/11 11:45:52 AM
219Optimization techniques in diesel engine system design
© Woodhead Publishing Limited, 2011
Section 3.2. More elaborated theories of RSM are introduced by Montgomery
(1991), Eriksson et al. (1999), and Myers and Montgomery (2002).
3.1.7 From single point to two-dimensional optimization
map
Diesel engine system design has two characteristics in output data. First, a
single ‘design point’ needs to be selected after comparing various solutions.
For example, a large amount of optimization can be conducted at the rated
power condition by comparing different hardware congurations and calibration
settings. However, in the end, one nominal design point needs to be selected
and reported as a nal summary in the system design. Secondly, parametric
maps are required during the course of system design to understand the
sensitivity and the data trend. The techniques of constructing the parametric
maps are important.
Diesel engine system design often handles a large number of factors.
Parametric analysis and its graphical display is a very important fundamental
technique every system design engineer must master. Graphical display of the
optimization results is very important for the following reasons. First of all,
during optimization not only is the nal optimal result needed, but also the
parameter sensitivity needs to be visually examined in order to obtain good
understanding. The parametric data also need to be documented for future
use or reference. Secondly, the design target is often a moving target during
the development stage. A complete graphical map covering the uncertainties
and the moving target is very convenient for system design to reference.
Therefore, running and reporting one single point of data is not sufcient in
engine system design. One- or two-dimensional maps are required. As one
more dimension is added in graphical display, the amount of information
packed increases exponentially. A useful graphical display usually has to be
limited to either a two-dimensional contour map (preferred) or an equivalent
three-dimensional cubic plot.
The one-dimensional map refers to plotting one factor (or response) on
the horizontal axis of the map and plotting one response on the vertical axis.
The two-dimensional map refers to plotting two factors or two responses on
the horizontal and vertical axes, respectively, and plotting another response
as constant-value contours.
A more powerful approach is to produce ‘each point’ in the one- or two-
dimensional map through optimization. The ‘optimization’ here is different
from the parametric sweeping introduced earlier. In the parametric sweeping
(Fig. 3.2), each point is obtained without optimization. One example of
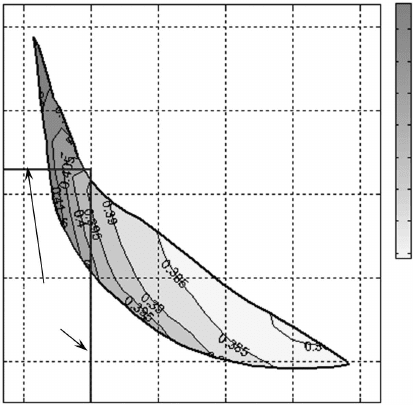
two-dimensional optimization is shown in Fig. 3.6. It presents the DoE
optimization result with respect to several factors (i.e., VGT vane opening,
EGR valve opening, fuel injection timing, and injection pressure). Two
Diesel-Xin-03.indd 219 5/5/11 11:45:53 AM
220 Diesel engine system design
© Woodhead Publishing Limited, 2011
responses, the brake specic NO
x
and the brake specic soot, are placed
on the horizontal and vertical axes of the map, respectively. The objective
function, BSFC, is minimized at ‘each’ point in such a two-dimensional
map subject to certain constraints (e.g., peak cylinder pressure, exhaust
temperature, plus the two additional constraints of the NO
x
and soot values
at that point). As a result, the BSFC contour map obtained as such is the
‘minimum BSFC’ map in an optimized sense within the design space and
bounded by the DoE factor range and optimization constraints. Such an
optimized contour map is certainly much more complex and computational
intensive than the simple parametric sweeping map shown in Fig. 3.2. The
two-dimensional optimization map is a very powerful graphical display and
a concise summary of the sensitivity and optimization results. The two-
dimensional optimization technique proposed here is especially important for
diesel engine system design because there are several critical trade-offs that
often need to be used in a two-dimensional domain. These trade-offs include:
(1) soot vs. NO
x
for emissions compliance (Fig. 3.6); (2) air–fuel ratio vs.
EGR rate for evaluating the air system capability; and (3) hydrocarbons vs.
exhaust temperature for aftertreatment design. Normally, minimizing BSFC
is appropriate in these two-dimensional optimizations.
In summary, there are ve fundamental techniques in the optimization of
diesel engine system design:
BSFC (lb/(hp.hr))
0.415
0.41
0.405
0.4
0.395
0.39
0.385
0.38
Emissions
limits
0.8 1 1.2 1.4 1.6 1.8
BSNO
X
(g/(hp.hr))
BSSoot (g/(hp.hr))
0.25
0.2
0.15
0.1
0.05
3.6 Two-dimensional optimization with minimum BSFC contour map.
Diesel-Xin-03.indd 220 5/5/11 11:45:53 AM
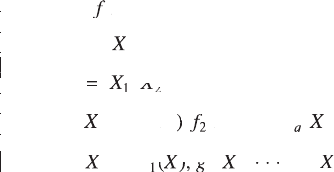
221Optimization techniques in diesel engine system design
© Woodhead Publishing Limited, 2011
∑ parametric sweeping
∑ DoE main effect plot
∑ DoE emulator
∑ one-dimensional optimization by curves
∑ two-dimensional optimization by contour maps.
3.1.8 From single-objective to multi-objective
optimization
Complete engine system optimization often requires meeting the requirements
of multiple objectives, such as performance, durability, packaging and cost.
The objectives of different attributes are usually con icting and have trade-
offs, for example, NO
x
vs. PM, fuel economy vs. emissions or engine noise.
Moreover, engine hardware design for the same attribute (e.g., volumetric
ef ciency, BSFC) also presents a trade-off between high speed and low
speed, or between high load and low load. Typical examples include
turbocharger matching and cam timing. Furthermore, engine operation in
customer usage occurs in a wide range of environmental conditions such
as hot and cold weather, low and high altitude. There is also a trade-off
for a given design attribute between those different conditions. Although
single-objective optimization is still a commonly used tool in engine system
design, more advanced multi-objective optimization is needed to address
these trade-offs.
A multi-objective optimization topic can be formulated as follows:
Min
imize
(
)
s
ubject to
()
≤ 0
wh
er
e
ere er
fX
(fX (
gX
()gX()
X
=
== =
[,
,
,
]
()
12
[,
12
[,
,
12
,
XX
[,XX[,
12
XX
12
[,
12
[,XX[,
12
[,
,
12
,XX ,
12
,
X
fX
()fX()
fX
1
fX
1
k
T
◊◊
◊
=
[)
fX[)fX
(fX([)(fX(
1
fX
1
[)
1
fX
1
),
[)),[)
(
),
,
()
]
()
fX
(fX (
fX
()fX()
gX
()gX()
g
q
fX
q
fX
T
fX
2
fX
(fX (
2
(fX (
◊◊
◊
=
[
12
1121
()
12
()
12
()
()
]
Xg
12
Xg
12
()Xg()
12
()
12
Xg
12
()
12
12
,
12
Xg
12
,
12
Xg
()Xg()
,Xg,
Xg
, Xg,
()X()
m
T
Xg◊◊Xg
Xg◊Xg
Ï
Ì
Ô
Ï
Ô
Ï
Ô
Ô
Ô
Ô
Ô
Ô
Ô
Ô
Ì
Ô
Ì
Ô
Ô
Ô
Ì
Ô
Ì
Ô
Ì
Ô
Ì
Ó
Ô
Ì
Ô
Ì
Ô
Ô
Ô
Ô
Ô
Ô
Ô
Ô
Ó
Ô
Ó
Ô
Ô
Ô
Ó
Ô
Ó
Ô
Ó
Ô
Ó
3.7
Optimization with multiple con icting objectives in a multi-dimensional
design space is dif cult. Multi-objective optimization may not have a single
optimum. Instead, there is a set of alternative trade-offs generally known as
the Pareto-optimal solutions. In any optimization study, it is necessary to
de ne an objective function, which can be either a single response parameter
or a predetermined combination of several parameters. Converting a multi-
objective optimization to a single-objective optimization can be problematic
because the optimization result can be in uenced by a bias in the selected
single objective function. Therefore, a direct exploration in a multi-objective
design space would be a better alternative. The solution methods for multi-
objective optimization topics usually include the following.
Diesel-Xin-03.indd 221 5/5/11 11:45:53 AM
222 Diesel engine system design
© Woodhead Publishing Limited, 2011
Single objective function with constraints
Select one criterion as primary and the remaining criteria as secondary. Use
the primary criterion as the objective function in the optimization, and assign
acceptable minimum or maximum values to the secondary criteria and use
them as constraints.
Non-normalized weighted single objective function
When the objectives are the same parameter or attribute with the same unit
but at different working conditions (e.g., BSFC or NO
x
emissions at different
engine speeds/loads or different ambient temperatures), apply weighting
factors on all the objective functions and then construct a single objective
function as follows:
FX
wf
Xw
w
j
q
jj
wf
jj
wf
j
Xw
j
Xw
i
q
i
()
FX()FX
=
(
wf (wf
Xw (Xw
jj
(
jj
wf
jj
wf (wf
jj
wf
)
Xw)Xw
Xw Xw
wh
XwwhXw
er
XwerXw
e
Xwe Xw
ere er
XwerXwe XwerXw
≥ 0,
w w
i
i
=
SS
XwSSXw
j
SS
j
Xw
j
XwSSXw
j
Xw
SS
XwSSXw
(SS (
wf (wfSSwf (wf
Xw (XwSSXw (Xw
jj
(
jj
SS
jj
(
jj
wf
jj
wf (wf
jj
wfSSwf
jj
wf (wf
jj
wf
)SS)
Xw)XwSSXw)Xw
whSSwh
XwwhXwSSXwwhXw
XwerXwSSXwerXw
Xwe XwSSXwe Xw
XwerXwe XwerXwSSXwerXwe XwerXw
≥ 0, SS ≥ 0,
==
11
jj
11
jj
j
11
j
i11i
==11==
i==i11i==i
111
3.8
or
FX
wf
Xf
j
q
jj
wf
jj
wf
j
Xf
j
Xf
target
()
FX()FX
[(
wf[(wf
Xf[(Xf
jj
[(
jj
wf
jj
wf[(wf
jj
wf
Xf)Xf
Xf – Xf
]
=
=
S
1
2
3.9
where a target value is denoted with the superscript ‘target’.
Normalized weighted single objective function
When the objectives are different parameters or attributes with different
units (e.g., emissions, BSFC, noise), construct a merit function as a single
objective by normalizing each parameter with their own reference values
or target values as follows:
FX
C
ww
ww
NO
NO
target
C
PM
PM
ta
r
x
ww
x
ww
x
()
FX()FX
=
+
ww +ww
5
12
ww
12
ww
12
ww
12
ww
ww
12
ww
target
12
target
ww
target
ww
12
ww
target
ww
12
ww
12
ww
ww +ww
12
ww +ww
1
y
y
y
y
Ê
Ë
12
Ë
12
Á
ww
Á
ww
12
Á
12
ww
12
ww
Á
ww
12
ww
Ê
Á
Ê
Ë
Á
Ë
12
Ë
12
Á
12
Ë
12
ˆ
¯
12
¯
12
˜
ww
˜
ww
12
˜
12
ww
12
ww
˜
ww
12
ww
ˆ
˜
ˆ
¯
˜
¯
12
¯
12
˜
12
¯
12
ge
ggeg
rgrgergr
t
C
HC
HC
target
C
CO
CO
t
w
w
Ê
Ë
Á
Ê
Á
Ê
Ë
Á
Ë
ˆ
¯
˜
ˆ
˜
ˆ
¯
˜
¯
Ê
Ë
Á
Ê
Á
Ê
Ë
Á
Ë
ˆ
¯
˜
ˆ
˜
ˆ
¯
˜
¯
+
23
C
23
C
Ê
23
Ê
ˆ
23
ˆ
3
4
+
y
y
y
y
ar
tart
aara
tatartat
ge
argear
t
C
BSFC
BSFC
target
p
ww
ww
BSFC
ww
BSFC
SP
L
SPLSP
Ê
Ë
y
Ë
y
Á
Ê
Á
Ê
Ë
Á
Ë
ˆ
¯
˜
ˆ
˜
ˆ
¯
˜
¯
◊
4
56
target
56
target
ww
56
ww
ww
56
ww
target
ww
target
56
target
ww
target
10
+
ww ww
ww
56
ww ww
56
ww
target
ww
target
56
target
ww
target
target
ww
target
56
target
ww
target
+
ww+ ww
ww
56
ww+ ww
56
ww
h
ww
h
ww
h
---
Ê
Ë
Á
Ê
Á
Ê
Á
Ë
Á
Ë
Á
Á
Á
ˆ
¯
˜
ˆ
˜
ˆ
˜
¯
˜
¯
˜
˜
˜
◊◊◊
È
Î
Í
È
Í
È
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Í
Î
Í
Î
Í
Í
Í
˘
˚
˙
˘
˙
˘
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˙
˚
˙
˚
˙
˙
˙
p
SP
L
SPLSP
target
20
+
CCC
6
3.10
where
y
NO
x
is brake speci c NO
x
emissions, h
BSFC
is brake speci c fuel
consumption, and p
SPL
is the sound pressure level of engine noise in dB. The
w
1
, w
2
, . . ., w
6
are weighting factors. The C
1
, C
2
, . . ., C
4
are the exponent
constants to amplify the effects of certain normalized terms. The C
5
and C
6
Diesel-Xin-03.indd 222 5/5/11 11:45:54 AM
223Optimization techniques in diesel engine system design
© Woodhead Publishing Limited, 2011
are also arbitrary coefcients. For example, C
5
= 1000, C
6
= –1 and C
1
= C
2
= . . . = 2 were used by Montgomery and Reitz (2000); C
5
= 1, C
6
= 1, C
1
= C
2
= . . . = 2 and w
1
= 1, w
2
= 1, w
3
= 0, w
4
= 0, w
5
= 1, w
6
= 0.5 were
used by Mallamo et al. (2004).
Pareto-optimal solutions
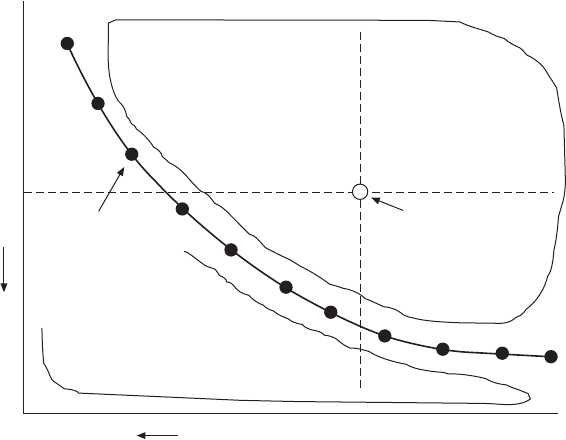
The concept of Pareto optimality is illustrated in Fig. 3.7. A Pareto-optimal
front curve or surface can be obtained by optimization algorithms such as the
multi-objective genetic algorithm (MOGA). In a single-objective optimization,
the optimal solution is usually clearly dened. However, this is not the case
for a multi-objective problem where the objectives can be conicting. A single
solution is hardly the best for all the objectives simultaneously. Instead of
a single optimum, there is a set of trade-off solutions, generally known as
Pareto-optimal solutions (also called non-dominated solutions). These solutions
are optimal in the sense that no other solutions in the design space are better
than them or can ‘dominate’ them when all the objectives are considered.
In other words, all other solutions are ‘dominated’ solutions that are worse
than the Pareto-optimal solutions. The method of Pareto-optimal solutions
has been widely used in engine optimization (Li et al., 2004; Courteille
et al., 2005; Zottin et al., 2008). A concept of Pareto front quality index
(PFQI) was developed by Kazancioglu et al. (2003) to objectively assess the
The solutions in this
area enclosed within the
boundary of design space
are worse than the Pareto-
optimal solutions
Indifferent region for ‘A’
In this region, the
solutions are worse
than solution ‘A’.
In other words, ‘A’
dominates this region
The points form an
optimal envelope
within the boundary
of design space, called
Pareto-optimal front
‘A’ is
dominated.
In this region, it is
hard to to differentiate
whether ‘A’ is better or
worse (i.e., indifferent)
Solution ‘A’
There are points better than
the Pareto-optimal solutions
but they are outside of the
boundary of design space
Good
Good
Objective 2 (e.g., engine noise)
Objective 1 (e.g., BSFC)
3.7 Illustration of Pareto optimality in two-objective optimization.
Diesel-Xin-03.indd 223 5/5/11 11:45:55 AM
224 Diesel engine system design
© Woodhead Publishing Limited, 2011
quality of Pareto optimal fronts; quantify the closeness to the utopia point
of the Pareto-optimal solutions; and quantify the range and the evenness of
the spread of the Pareto solutions.
Minimum-contour-based multiple Pareto-optimal solutions
In the past a Pareto optimal front was obtained by running an optimization
routine. Using the two-dimensional optimization (minimization) contour
map discussed in the previous section, the Pareto optimal can be generated
more easily and exibly. Taking an example of the DoE optimization shown
in Fig. 3.8, the method of minimum-contour-based multiple Pareto-optimal
solutions is explained as follows. The objective is to nd the optimal
solution of emissions level, BSFC and cost. A DoE can be constructed at
a representative engine operating condition in speed and load. The DoE
factors include air system control factors (e.g., VGT vane opening, EGR
valve opening, intake throttle opening, and wastegate opening) and fuel
injection control factors (e.g., main injection timing, post injection timing
and quantity, fuel injection pressure). The DoE responses include air–fuel
ratio, EGR rate, engine-out NO
x
, engine-out soot, BSFC, and turbine outlet
exhaust gas temperature. Aftertreatment operation (e.g., DPF regeneration)
prefers hotter exhaust gas temperature in order to save cost from precious
metal loading inside the DPF. But hotter exhaust gas may indicate more
energy is lost or wasted and hence worse BSFC. Therefore, there is a trade-
off between exhaust temperature and BSFC. Moreover, the emissions level
affects such a trade-off. The total cost of the system for the customer is
related to the emissions level the engine is designed for, the aftertreatment
cost, and the cost saving from the fuel saving due to BSFC reduction. There
may be an optimal (the lowest) cost within the design space.
Obviously, optimizing such a multi-dimensional design topic and presenting
the result in a concise way is challenging. The minimum-contour-based
method is characterized by the following three steps.
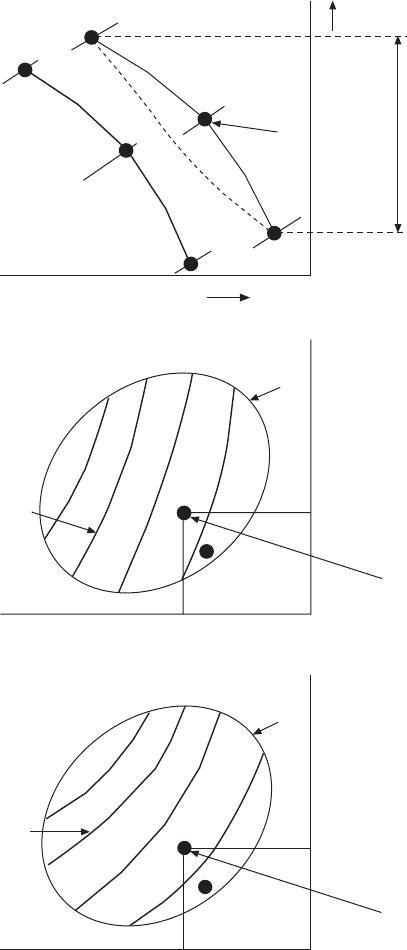
∑ Step 1 – minimum-contour optimization for the rst objective (Fig.
3.8a). The method starts from conducting constrained single-objective
optimization to minimize BSFC in the entire emissions domain (i.e., the
soot vs. NO
x
domain). The range of the DoE factors forms a boundary in
this response domain. Every data point on the minimum BSFC contour
map has the minimum achievable BSFC within the factor space. In other
words, if a third axis were created to represent BSFC pointing vertically
out of the paper from point A, there would be multiple BSFC values
which are higher than the minimum value shown in the contour map at
that given emission value. Once the minimum BSFC map is obtained,
several points such as A and A¢ at different emissions levels can be
identied.
Diesel-Xin-03.indd 224 5/5/11 11:45:55 AM
© Woodhead Publishing Limited, 2011
Engine-out soot (or A/F ratio)
Engine-out soot (or A/F ratio)
Good BSFC
DoE boundary
Engine-out NO
x
(or EGR rate) Engine-out NO
x
(or EGR rate)
Exhaust gas temperature
DoE range
Minimum BSFC meeting emissions
(a) Step 1: Minimum-contour
optimization for the first objective
(b) Step 2: Maximum-contour
optimization for the second objective
(c) Step 3: multiple Pareto-optimal
curves at different constraints, and
optimization
Minimum exhaust T meeting emissions
Minimum BSFC constant contours
Maximum exhaust temperature
contours
DoE boundary
Emissions
box
Emissions
box
A¢
C¢
A
Good
0.33
500 F
600 F
700 F
800 F
0.32
0.31
0.30 lb/hp.hr
C
$1100
$700
$900
$800
$1000
C
C¢
B¢
A¢
0.1g soot
0.07g soot
0.9g NO
x
0.4g NO
x
Total system life or cost
$1000
Optimum
3.8 Illustration of minimum-contour-based multiple Pareto optimal solution.
Diesel-Xin-03.indd 225 5/5/11 11:45:55 AM
