Xin Q. Diesel Engine System Design

236 Diesel engine system design

DoE method: D-Optimal

DoE emulator does not

use interaction terms

Average error of emulator

suface ﬁ tting is 0.3548%

DoE method: D-Optimal.

DoE emulator uses

interaction terms

Average error of emulator

surface ﬁ tting is 0.0485%

Emulator

GT-POWER

Emulator

GT-POWER

0 10 20 30 40 50 60 70 80

DoE run number

0 10 20 30 40 50 60 70 80

DoE run number

BSFC (lb/(hp.hr))BSFC (lb/(hp.hr))

0.425

0.42

0.415

0.41

0.405

0.4

0.395

0.39

0.385

0.38

0.375

0.425

0.42

0.415

0.41

0.405

0.4

0.395

0.39

0.385

0.38

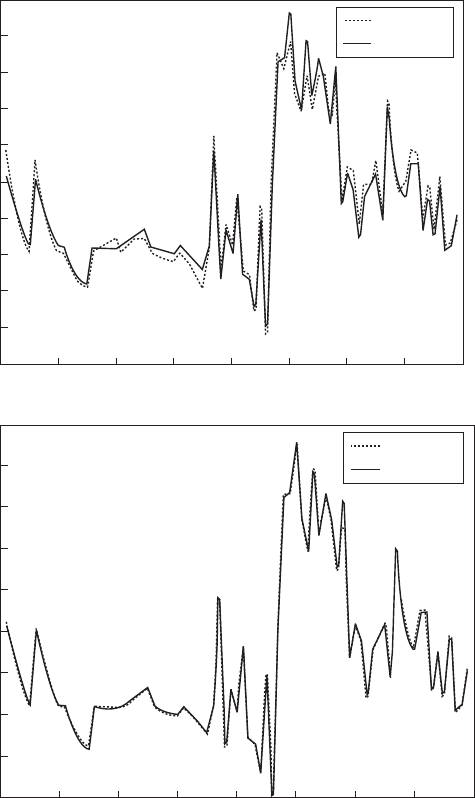
3.13 RSM emulator model accuracy – effect of interaction terms.

Montgomery (2002). Note that the number of DoE runs needs to be no less

than the number of regression coef cients in equation 3.15, i.e., n ≥ p.

A coef cient of determination

R

d

R

d

R

2

(also called explained variance or

goodness of  t) is de ned as the ratio of the regression sum of squares to the

total sum of squares. The total here refers to the regression sum of squares

plus the residual sum of squares, as shown in equation 3.17:

Diesel-Xin-03.indd 236 5/5/11 11:45:59 AM



Second-order data ﬁt in a DoE at rated power

Third-order data ﬁt in a DoE at rated power

Predicted values

Residuals

Predicted values

0.5

0.45

0.4

0.35

3200

3000

2800

2600

2400

2200

2000

2500

2000

1500

1000

500

0

0.04

0.03

0.02

0.01

0

–0.01

50

0

–50

1500

1000

500

0

–500

8

6

4

2

0

–2

–4

30

20

10

0

–10

–20

–30

300

200

100

0

–100

–200

0.55

0.5

0.45

0.4

0.35

3500

3000

2500

2000

1500

4000

3000

2000

1000

0

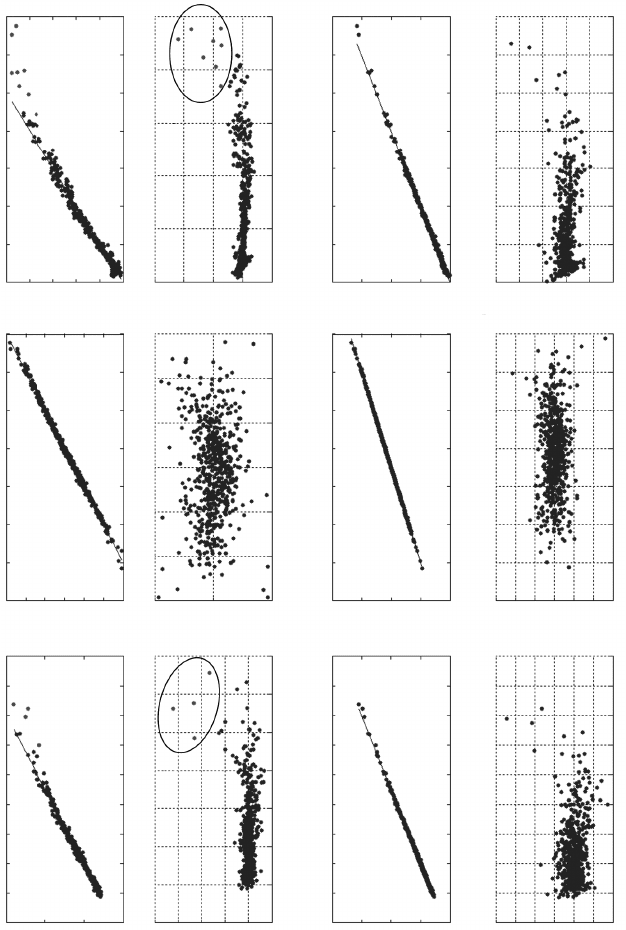
55 coefﬁcients for 9 factors

615 DoE cases

220 coefﬁcients for 9 factors

615 DoE cases

R

2

= 0.99

RMSE = 0.0019

R

2

= 0.996

RMSE = 12

R

2

= 0.983

RMSE = 61

R

2

= 0.998

RMSE = 0.00087

R

2

= 1

RMSE = 4.2

R

2

= 0.997

RMSE = 28

0.36 0.38 0.4 0.42 0.44 0.46 0.48 0.5 0.52 0.54

Measured values: BSFC (lb/(hp.hr))

Outliers

Engine ‘delta P’ is

highly nonlinear

1800 2000 2200 2400 2600 2800 3000 3200

Measured values: peak cylinder temperature (°F)

2000 2200 2400 2600 2800 3000 3200

Predicted values: peak cylinder temperature (°F)

1800 2000 2200 2400 2600 2800 3000 3200

Measured values: peak cylinder temperature (°F)

1800 2000 2200 2400 2600 2800 3000 3200

Predicted values: peak cylinder temperature (°F)

0 500 1000 1500 2000 2500 3000 3500

Measured values: engine delta P (exhaust manifold P minus intake

manifold P) (mbar)

0 500 1000 1500 2000 2500

Predicted values: engine delta P (exhaust

manifold P minus intake manifold P) (mbar)

0 500 1000 1500 2000 2500 3000 3500

Measured values: engine delta P (exhaust

manifold P minus intake manifold P) (mbar)

0 500 1000 1500 2000 2500 3000 3500

Predicted values: engine delta P (exhaust

manifold P minus intake manifold P) (mbar)

0.36 0.38 0.4 0.42 0.44 0.46 0.48 0.5

Predicted values: BSFC (lb/(hp.hr))

0.36 0.38 0.4 0.42 0.44 0.46 0.48 0.5

Measured values: BSFC (lb/(hp.hr))

0.36 0.38 0.4 0.42 0.44 0.46 0.48 0.5 0.52 0.54

Predicted values: BSFC (lb/(hp.hr))

3.14 RSM emulator model accuracy – effect of surface ﬁt order.

Diesel-Xin-03.indd 237 5/5/11 11:46:00 AM



238 Diesel engine system design

R

S

Y

d

SR

S

SR

S

ST

S

ST

S

SE

S

SE

S

ST

S

ST

S

r

n

obs

Y

obs

Y

r

2

=1

,

=

S

= 1 –

(

–

S

YYY

YY

r

YYY

r

YYY

r

n

obs

YY

obs

YY

r

YY

r

YY

obs

YY

obs

YY

)

(

YY – YY

)

2

=1

,

2

S

and 0 ≤

R

d

2

≤ 1 3.17

As pointed out by Myers and Montgomery (2002), a value of

R

d

R

d

R

2

close to

1 does not necessarily imply that the regression model is good for accurate

prediction. Adding a polynomial term to the model always increases

R

d

R

d

R

2

because the least-squares solution for equation 3.16 approaches a deterministic

solution with

R

d

2

= 1, regardless of whether the additional term is statistically

signi cant or not. If adding an additional term in the emulator results in a

small increase in

R

d

2

, it suggests that the term does not really improve the

model. It is possible to have a model with

R

d

2

close to 1, but the prediction

of the response has poor accuracy due to the negative impact of irrelevant

terms in the model. More regression terms do not necessarily mean better

model accuracy or predictability because the irrelevant terms which do not

re ect the physical nature may interfere with the model’s predictability. This

is especially true for the interaction terms. Model accuracy checking and

model pruning to delete irrelevant terms are always necessary to ensure the

 tted model represents the true system behavior adequately.

To overcome the problem with

R

d

2

, an adjusted

R

adj

R

adj

R

2

(also called explained

variance) is used in the literature (e.g., Myers and Montgomery, 2002):

R

S

np

S

n

adj

SE

S

SE

S

ST

S

ST

S

2

1

= 1 –

np – np

–

= 1 –

Ê

Ë

Ê

Ë

Ê

Á

Ê

Ë

Á

Ë

Ê

Ë

Ê

Á

Ê

Ë

Ê

ˆ

¯

ˆ

¯

ˆ

˜

ˆ

¯

˜

¯

ˆ

¯

ˆ

˜

ˆ

¯

ˆ

Ê

Ë

Ê

Ë

Ê

Á

Ê

Ë

Á

Ë

Ê

Ë

Ê

Á

Ê

Ë

Ê

ˆ

¯

ˆ

¯

ˆ

˜

ˆ

¯

˜

¯

ˆ

¯

ˆ

˜

ˆ

¯

ˆ

nnn

np

R

d

R

d

R

1

np – np

(

1 –

)

2

–

and

RR

adj

RR

adj

RR

d

2

RR

2

RR

<

RR <RR

2

3.18

where n is the number of DoE runs or observations, and p is the number

of regression coef cients in the model. In general, if unnecessary terms

are added, the value of

R

adj

2

will often decrease. When

R

d

2

and

R

adj

2

differ

dramatically, there is a good chance that insigni cant terms have been used in

the emulator model (Myers and Montgomery, 2002). When less useful model

terms are removed,

R

d

2

decreases and

R

adj

2

normally remains unchanged.

This is a method to test or judge which polynomial terms are important in

the model. The details of S

SE

, S

ST

and S

SR

functions are given in Myers and

Montgomery (2002). A parameter of goodness of prediction is the predicted

variation

R

pr

edictio

n

2

,

given by

R

S

Y

pr

edictio

n

PRES

S

ST

S

ST

S

r

n

obs

Y

obs

Y

2

= 1 –

(

=1

,

u

S

rr

rrrr

r

n

obs

r

obs

pr

edic

Y

rr

Y

rr

YY

obs

YY

obs

r

YY

r

obs

YY

obs

R

–

rr

–

rr

)

(

YY – YY

)

– ∞ ≤

()

rr()rr

Y

()

Y

rr

Y

rr()rr

Y

rr

2

=1

,

2

ˆ

S

tio

ttiot

n

2

≤ 1

Ï

Ì

Ô

Ï

Ô

Ï

Ô

Ì

Ô

Ì

Ô

Ó

Ô

Ì

Ô

Ì

Ô

Ó

Ô

Ó

Ô

3.19

Diesel-Xin-03.indd 238 5/5/11 11:46:01 AM



239Optimization techniques in diesel engine system design

where

u

PRES

S

is the prediction error sum of squares, and

ˆ

Y

()

Y

()

Y

r()r

is the predicted

response at rth observation by using the emulator regression model  tted

just without using the rth observation run. Such an approach is also called

‘leave-one-out’ cross validation (Bates et al., 2000). The cross validation

predicts each DoE run in turn when that run point is left out of the emulator

equation.

R

pr

edictio

n

2

indicates the predictive capability of the original regression

model that is  tted with all the runs from n observations.

R

pr

edictio

n

2

is more

realistic and useful than

R

adj

2

and

R

d

2

to judge the quality of the regression

models. Generally speaking,

R

pr

edictio

n

2

should be greater than 0.8–0.9 in

order for a model to be acceptable. Moreover,

R

pr

edictio

n

2

and

R

d

2

should

not be separated by more than 0.2–0.3. Figure 3.13 shows an example of

the importance of a second-order interaction term in an air system DoE

simulation. Figure 3.14 shows an example of the importance of the third-

order terms in the emulator.

Another parameter to characterize the goodness of prediction or accuracy of

the emulator model is the estimated root-mean-square error (RMSE). RMSE

allows an estimation of the con dence intervals for model prediction. Larger

error bars indicate less con dence in the emulator. According to Bates et

al. (2000), an index of the inaccuracy of the emulator is de ned as a RMSE

percentage of the range of the response, given by

f

YY

RM

f

RM

f

SE

RMSERM

RM

SE

RMSERM

obs

YY

obs

YY

ma

YY

ma

YY

x

YY

x

YY

maxma

YY

ma

YY

x

YY

ma

YY

obs

YY

obs

YY

mi

n

%

= 100

YY – YY

= 100

,,

ma,,ma

x,,x

maxma,,maxma

obs,,obs

¥

u

1

(

)

=1

()

,

2

,,

n

YY

– YY –

()

YY

()

YY

– YY –

r

n

()r()

()

YY

()r()

YY

()

obs

YY

obs

YY

r

obs

YY

obs

YY

ma

,,ma,,

YY

ma

YY

x

,,x,,

YY

x

YY

maxma

,,ma,,x,,ma,,

YY

ma

YY

x

YY

ma

YY

obs

,,obs,,

YY

obs

YY

mi

n

S

ˆ

3.20

For example, f

RMSE%

= 5% means that if the emulator is used to predict the

response at a new factor setting, the error of prediction can be expected to

be roughly less than 5% when compared with the true value. A very narrow

bar of con dence error indicates good statistical con dence in the prediction.

A perfect emulator would produce predicted response values that overlap

the true values with zero-length error bars.

Residual analysis and testing for lack-of- t are common techniques for

model accuracy checking. Choosing the right polynomial terms and deleting

irrelevant terms in the model is a key step to ensure model accuracy. Adding

DoE runs by using more factor levels and factor interactions usually can

improve model accuracy and predictability but at the expense of longer time

or higher cost for the runs. Good RSM DoE designs allow the estimation of

the model coef cients with low uncertainty. The low uncertainty is measured

by narrow error bars of the model’s regression coef cients. A con dence

interval refers to the interval between an upper bound and lower bound for

an estimate at a selected degree of certainty (e.g., 95%). A prediction interval

Diesel-Xin-03.indd 239 5/5/11 11:46:02 AM



240 Diesel engine system design

refers to the bounds for a predicted value of the response by using the model.

A good example of the RSM model regression and optimization for diesel

engine performance was given in the Chapter 15 in the book by Eriksson et

al. (1999). Moreover, modern optimization software packages (e.g., MODDE,

iSIGHT, Minitab) usually outputs the calculations of ANOVA, main effect,

and interaction effect as standard post-processing of the DoE.

Lastly, it also should be noted that the transformation of factor and/or

response variables from their natural unit to special forms (e.g., natural log,

exponential, or trigonometric) may better reect the physical mechanisms

of the system hence improve the t of the model to the DoE data runs. For

example, a new response Y* can be obtained by the transformation of the

original response Y* = Y

0.5

or Y* = lnY before surface t is performed. Such

a transformation may replace the higher-order polynomial terms for highly

nonlinear phenomena or special curvatures. The transformation may also

eliminate certain interaction terms from the emulator model so that the model

can be simplied with better accuracy. Note that the transformed model is

still classied as a polynomial model.

3.2.3 Statistical DoE design for RSM

The RSM technique can be applied to both experimental testing and

simulation. There are three major differences between experimental tests

and simulation:

1. Any experimental work always contains measurement errors or variability.

The input or output of test runs are not exactly repeatable. Simulation

does not have this problem. Therefore, a randomized order of DoE

runs and the repeated center-point runs for replicate errors used in an

experimental DoE are not necessary in a simulation DoE.

2. Hardware limitations (e.g., excessively high peak cylinder pressure) mean

that some experimental runs cannot be obtained within the designed DoE

factor space so that these data points are simply missing. Simulation is

not limited by such real world constraints. Extreme but still meaningful

data sometimes can be obtained easily in the simulation and are included

as useful information to build the emulator.

3. Simulation is usually much faster and less expensive than experimental

testing. For example, a computer model can run overnight automatically

without human intervention for a large number of DoE runs.

Overall, simulation usually has less restrictive or less demanding requirements

on the statistical DoE design than experimental testing. Due to the above

three reasons, the statistical DoE design method used for simulation can

be different from the DoE method used for experimental testing. Although

experimental data analysis such as emissions calibration or hardware testing

Diesel-Xin-03.indd 240 5/5/11 11:46:02 AM



241Optimization techniques in diesel engine system design

is an important part in diesel engine system design, the main body of the

system design work is conducted by simulation. The focus of this section is

on the statistical DoE design of RSM used for engine system simulations.

Myers and Montgomery (2002) provide a thorough discussion of the principles

of experimental DoE design. Interested readers can nd theoretical analysis

and practical guidelines there for designing experiments.

The two most important properties of DoE design for engine system

simulation are good emulator accuracy and cost-effective computation.

Between them, good emulator accuracy has paramount importance for the

quality of engine system design. Therefore, unlike experimental DoE tests

where a minimum number of DoE runs is often a primary objective of the

test, simulation DoE work usually uses as many DoE runs as possible (at

affordable computing time) in order to increase the accuracy of the emulator

model.

The emulator model accuracy is affected by the following: (1) the order

and the number of the terms in the model (discussed in the previous section);

(2) the number of DoE runs; (3) the factors (factor types, factor range, and

factor levels); and (4) the distribution pattern of the DoE runs in the factor

space (i.e., DoE design properties, interactions). These aspects are discussed

below.

Engine design and operating factors can be classied into control factors

and noise factors. The number of factors built into a RSM model needs to

be carefully planned because too many factors will result in an excessively

large number of DoE runs (Fig. 3.15) and poor accuracy in surface t. The

‘shbone’ diagram introduced in Chapter 1 can be used to brainstorm all

possible inuential factors. Unlike the Taguchi DoE method where the control

factors and noise factors are separated into two different DoE arrays, the

control and noise factors in a RSM DoE can be mixed more efciently in one

DoE array. Factor screening and range screening can be conducted with a rst

DoE by using a rst-order model and a large number of factors along with a

large factor range in order to identify important main effects and interaction

effects. Fewer important factors along with a relatively smaller factor range

around the optimum can be identied and built into a second rened DoE

by using a higher-order emulator model in order to achieve better resolution

for optimization. The factor range needs to reect the operation region that

can be neither too small nor too large. A too small range may result in an

important factor behaving insignicantly or like a constant in the emulator

model so that it does not provide much value to reect its sensitivity in the

DoE. A too large range often results in an extreme combination of the factor

settings that may give unreasonable or impossible simulation results. For

example, when the exhaust restriction is excessively high and the turbine

area is extremely large, it will result in an extremely low air–fuel ratio that

is even below the stoichiometric value.

Diesel-Xin-03.indd 241 5/5/11 11:46:02 AM



242 Diesel engine system design

Once the number of factors and the factor ranges are determined, a DoE

design method needs to be selected to generate the factor levels and the

DoE runs. Different design methods give a different size of the DoE and

different accuracy and predictability of the emulator model. The selection of

factor levels depends on the emulator model structure (i.e., the order and the

DoE runs of

3-level full

factorial 3

k

DoE runs of

2-level full

factorial 2

k

DoE runs of

3-level fractional

factorial 3

k–1

DoE runs of

2-level fractional

factorial 2

k–1

3

k–2

3

k–3

2

k–2

2

k–3

2 4 6 8 10 12 14 16 18 20

Number of DoE factors

2 4 6 8 10 12 14 16 18 20

Number of DoE factors

Required number of DoE runs or

number of emulator model terms

Minimum required number of DoE runs

150

100

50

0

500

450

400

350

300

250

200

150

100

50

0

3-level full

factorial

3rd order ﬁt for

3 factors (2nd

order ﬁt for the

rest factors)

3-level

CCF

3-level

D-Optimal

2nd order

ﬁt for all

factors

Emulator terms

of 1st-order with

interaction

Emulator terms

of 2nd-order

with interaction

3.15 DoE factors and number of DoE runs.

Diesel-Xin-03.indd 242 5/5/11 11:46:03 AM



243Optimization techniques in diesel engine system design

interaction terms used) and the DoE design method. Two-level DoE designs

are sufcient for tting the models that contain the rst-order main effects

and the low-order interactions, such as those used in the screening analysis.

If a second-order model is needed (e.g., for the purpose of optimization), the

factor needs to have at least three levels in order to estimate the quadratic

terms. If a third-order model is needed, the factor needs to have at least four

levels. The minimum required number of DoE design points (or runs, denoted

as n) also depends on the emulator model structure: n ≥ p, where p is given

by equation 3.15. Figure 3.15 shows the number of DoE runs required in

some particular DoE designs. The number of runs depends on the number

of factors, DoE design method, and the polynomial order of accuracy of the

emulator. Moreover, it should be noted that in order to ensure good resolution

in factor spacing in the experimental DoE design, the interval between the

levels needs to be large enough to cover three times the standard deviation

of the factor during the experimental test. However, such a restriction and

the issue of statistical scattering do not exist in a simulation DoE.

The statistical DoE design method affects the efciency and quality of

RSM emulator model building. The theory of the statistical properties of

factorial designs is very complex. Many conclusions depend on the physical

nature of the problem or assumed regression model. Some general guidelines

for statistical DoE design are summarized below.

The rst guideline is to use full factorial and fractional factorial designs

appropriately. Full factorial design provides the most complete information

to describe the relationship among the factors. But a full factorial design

with more than three levels is not practical for engine system simulations

when the number of factors is more than ve or six due to the excessively

large number of DoE runs (Fig. 3.15). Moreover, compared to the much more

efcient fractional factorial design, full factorial design is often not necessary

because it provides only marginally more information at the expense of a

huge increase in the number of DoE runs.

To further illustrate the role of factorial design on the emulator model

structure, consider the 2

4

full factorial design with four factors X

1

, X

2

, X

3

and X

4

at two levels, –1 and +1 (Table 3.3) for a rst-order emulator model.

The number of DoE runs is 2

4

= 16. It is possible to estimate at maximum

16 model coefcients for all the effects contained in these 16 runs. The

coefcients are distributed as follows: 1 constant term, 4 rst-order terms

(without the second-order terms due to only two factor levels), 6 two-factor

interactions, 4 three-factor interactions, and 1 four-factor interaction. The

corresponding model structure of the emulator is:

Y = C

0

+ C

1

X

1

+ C

2

X

2

+ C

3

X

3

+ C

4

X

4

+

C

5

X

1

X

2

+ C

6

X

1

X

3

+ C

7

X

1

X

4

+ C

8

X

2

X

3

+ C

9

X

2

X

4

+ C

10

X

3

X

4

+

C

11

X

1

X

2

X

3

+ C

12

X

1

X

2

X

4

+ C

13

X

2

X

3

X

4

+ C

14

X

3

X

4

X

1

+

C

15

X

1

X

2

X

3

X

4

3.21

Diesel-Xin-03.indd 243 5/5/11 11:46:03 AM



Table 3.3 Illustration of full factorial design and confounding effects in fractional factorial design

Full factorial design Fractional factorial design

DoE run number X

1

X

2

X

3

X

4

DoE run number X

1

X

2

X

3

X

4

(generator constructed by the sign of

X

1

· X

2

· X

3

)

1 –1 –1 –1

–1

1 –1 –1 –1

–1

2 +1 –1 –1

–1

10 +1 –1 –1

+1

3 –1 +1 –1

–1

11 –1 +1 –1

+1

4 +1 +1 –1

–1

4 +1 +1 –1

–1

5 –1 –1 +1

–1

13 –1 –1 +1

+1

6 +1 –1 +1

–1

6 +1 –1 +1

–1

7 –1 +1 +1

–1

7 –1 +1 +1

–1

8 +1 +1 +1

–1

16 +1 +1 +1

+1

9 –1 –1 –1 +1

10 +1 –1 –1 +1 DoE run number X

1

X

2

X

3

X

4

(generator constructed by the sign of

–X

1

· X

2

· X

3

)

11 –1 +1 –1 +1 9 –1 –1 –1 +1

12 +1 +1 –1 +1 2 +1 –1 –1 –1

13 –1 –1 +1 +1 3 –1 +1 –1 –1

14 +1 –1 +1 +1 12 +1 +1 –1 +1

15 –1 +1 +1 +1 5 –1 –1 +1 –1

16 +1 +1 +1 +1 14 +1 –1 +1 +1

15 –1 +1 +1 +1

8 +1 +1 +1 –1

Diesel-Xin-03.indd 244 5/5/11 11:46:03 AM



245Optimization techniques in diesel engine system design

It is found that usually the lower order terms are relatively more important

than the higher order terms in the emulator, and the three-factor or four-

factor interaction terms are negligible to the response. This means that there

is usually a redundancy in such an emulator model as equation 3.21 for the

full factorial design. Those redundant runs corresponding to the higher-order

interaction terms can be eliminated without affecting the accuracy of the

emulator model. Fractional factorial designs address how to reduce such a

redundancy. Moreover, fractional factorial design is very useful in screening

many factors with a minimum number of runs.

Confounding is the most important concept in fractional factorial design.

Confounding means when the number of DoE runs and the number of

terms in the emulator model are reduced from the full factorial design,

the estimated coefcients of the remaining terms in the model actually

represent the combined factor effects mixed up with each other (i.e., the

effects cannot be estimated completely independently from each other). In

the above example, if the number of DoE runs has to be reduced to 8 (i.e.,

a fractional factorial design 2

4–1

= 8) from 16 (i.e., the full factorial design

2

4

= 16), the maximum allowable terms in the emulator has to be reduced

to 8 from equation 3.21 accordingly. There are two questions here: (1) How

to reduce the number of DoE runs? (2) Which terms in equation 3.21 must

be deleted accordingly? These questions are answered as follows.

From Table 3.3, it is observed that if only the DoE runs 1–8 are used,

although all the main and interaction effects of the factors X

1

, X

2

and X

3

are

completely captured, the effects of X

4

are completely missed. As a result,

all the terms involving X

4

in the emulator in equation 3.21 must be deleted.

A similar argument applies for other factors. Therefore, the factor levels of

X

4

in the DoE runs 1–8 have to be changed differently compared with the

levels used in the full factorial design in order to add certain effects of X

4

.

In the fractional factorial example in Table 3.3, the main effects of all the

factors can still be clearly estimated even if X

4

changes its level settings.

However, there is a penalty that certain interaction effects are mixed or cannot

be estimated clearly due to the factor level change of X

4

. Such an effect is

called ‘confounding’ when a full factorial design is reduced to a fractional

factorial design. Confounding is essentially the inability to separate DoE

information about individual factors or interactions.

There are generally two types of confounding generator methods: one

using the original sign of the product of other factors for the generator (e.g.,

X

4

= X

1

X

2

X

3

); and the other using the negative sign (e.g., X

4

= – X

1

X

2

X

3

).

The two generator methods are shown in Table 3.3 for the two fractional

factorial designs constructed for X

4

as the generator. Note that in this example

the four factors are rotatable (i.e., they are equally switchable among the

factors). However, in the scenarios with more factors, the confounding pattern

may be regulated in a desired direction or for a desired factor by adjusting

Diesel-Xin-03.indd 245 5/5/11 11:46:03 AM



Xin Q. Diesel Engine System Design

Подождите немного. Документ загружается.