Wong H.-S.P., Akinwande D. Carbon Nanotube and Graphene Device Physics

Подождите немного. Документ загружается.

8.3 Surface potential 199

where c

and c

are the Taylor series coefﬁcients given by the lengthy expressions

X [C

T )

+ e

(2m+1)E

/2k

]

(8.9)

where

X = e

/2k

+ Ae

/2k

Y = e

/2k

+ Ae

Z = Ae

(4m+1)/2k

T − mE

) + e

(m+1)/k

T + mE

)

(2m+1)E

/2k



2mE

− e





/2k

+ A e



+ e

(2m+1)E

/2k

. (8.10)

The useful property of these cumbersome expressions is that they explicitly

capture the dependence on C

, bandgap, and temperature, albeit in a somewhat

complex manner. Ideally, if C

was linearly symmetric about eϕ

= 0.5E

then a

natural choice for m corresponding to that point would be ∼0.25/e. However, C

generally not symmetric, as such, a value of m ∼(0.27/e) −(0.33/e) is found to give

the best agreement with numerical self-consistent computation. Finally, solving

for ϕ

in Eq. (8.8) yields the analytical surface potential in the semiclassical limit.

≈

+ t

, (8.11)

with s and t related to the Taylor series coefﬁcients by

s =

, t =

. (8.12)

A similar analysis for holes (V

< 0) produces the same expression for the

surface potential with the exception that V

in the denominator of Eq. (8.11)is

replaced with |V

|. Employing Eq. (8.11), we arrive at a ﬁnal algebraic relation

for the surface potential reﬂecting the inﬂuence of the gate in the quantum and

semiclassical limits:

≈ V

− V



1 −

s|V

|+t





1 −

s|V

|+t



. (8.13)

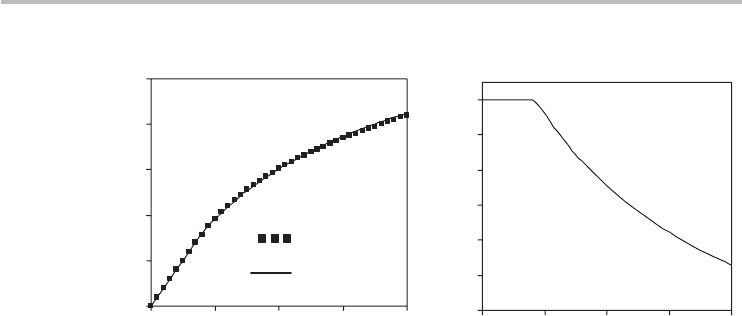
Figure 8.3 shows the surface potential computed numerically and analytically for

an example two-terminal top-gated CNT device. One terminal is the gate electrode

and the other terminal is the source and drain electrodes, which have been shorted

together (standard device connection for CNT capacitance measurements). The s

200 Chapter 8 Carbon nanotube ﬁeld-effect transistors

0.1

0.2

0.3

0.4

0.5

0 0.2 0.4 0.6 0.8

00.20.40.60.8

for 1.5 nm CNT, and

HfO

oxide (k =15, t

= 8 nm)

Self-consistent

computation

Analytical

calculation

0.4

0.5

0.6

0.7

0.8

0.9

(V)

(a) (b)

Fig. 8.3 Characteristic proﬁle of the CNT surface potential. Analytical ϕ

using best-ﬁt parameters

(s = 1.41V

−1

, t = 0.76) compared with self-consistent computation showing good

agreement (peak error < 5 %). C

∼ 264.96 aF µm

−1

. (b) Analytical ϕ

revealing

that, at low voltages, V

has maximum control of the surface potential which gradually

weakens at higher voltages.

and t parameters used in Figure 8.3 (s = 1.41 V

−1

, t = 0.76) are the best-ﬁt values

obtained empirically by curve ﬁtting Eq. (8.13) to the numerical results. Using

m = 0.275/e and Eq. (8.12), the estimated analytical values for s and t are 1.52

−1

and 0.83 respectively, which are within 10 % of the best-ﬁt values.

In summary, the Taylor series approximation has revealed that the appropriate

analytical form for the surface potential is Eq. (8.13) to ﬁrst order, which shows

very strong agreement with numerically computed values of ϕ

. Additionally, the

analytical parameters (s and t) canbe determined from the Taylor series coefﬁcients

with increasing accuracy as C

becomes smaller than unity.

8.4 Ballistic theory of ohmic-contact CNFETs

Employing the analytical surface potential discussed in the previous section, we

are now in a position to develop an analytical theory for CNFETs and thereby come

to an understanding of their basic transistor properties and performance metrics.

Of the four CNFETs identiﬁed in Table 8.1, the ballistic ﬂavor with ohmic or

transparent contacts is the most attractive because it allows for the smoothest ﬂow

of current, leading to superior performance compared with the other three ﬂavors

of CNFETs. As a result, our focus here will be on the ballistic CNFET with ohmic

contacts. An added beneﬁt is that the ballistic CNFET is actually the simplest

CNFET to study mathematically,

leading to deep insights that can be extended

While it is true that the ballistic CNFET is the easiest to study, it will not be fair if we failed to

mention that it is by far the most challenging of CNFETs to fabricate for reasons related to the

8.4 Ballistic theory of ohmic-contact CNFETs 201

High-k

> 0

S D

= 0

High-k

n++

intrinsic

= 0

> 0

(a) (b)

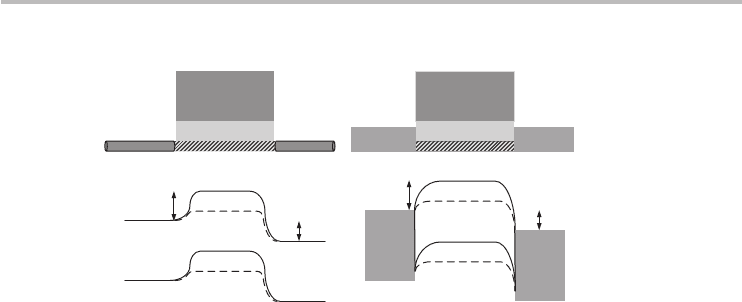
Fig. 8.4 Top-gated n-type CNFET device geometries considered within the ballistic model. (a) A

CNFET with doped CNT ohmic contacts and its band diagram. (b) A self-aligned CNFET

with ohmic metallic contacts and its band diagram (k = 15, t

= 8 nm for the

experimental and analytical CNFETs analyzed in this section). Note that while electrons

experience an ohmic contact, holes, on the other hand, experience a Schottky barrier.

to the other types of CNFET in Table 8.1. Invariably, we expect a successful

transistor theory to capture all the pertinent parameters, including temperature and

bandgap. Additionally, the external voltages by which the charge and current are

controlled must be explicitly reﬂected in the transistor theory in order for the theory

to be of any use.

Ballistic transport in CNTs applies when the channel length is much smaller than

the electron mean free path l

. In high-quality semiconducting CNTs operating

around room temperature and at low energies, l

is essentially determined by

electron scattering from acoustic phonons which results in a mean free path of the

order of 0.5 µm.Therefore, high-quality CNFETs with channellengths 50 nmare

naturally suited for ballistic operation. Notably,the ballistic CNFET can be realized

in any of the device geometries shown in Figure 8.4. provided the channel length

and contacts satisfy the expected criteria. Figure 8.4 shows the simpliﬁed device

geometry of two top-gated CNFETs and associated band diagrams. In essence, the

gate voltage controls the energy barrier for current ﬂow between the source and

drain electrodes, while the source and drain voltages control the source and drain

Fermi levels respectively.

The current–voltage (I −V ) relationship for a ballistic CNFET can be con-

structed from Planck’s quantum postulate. An alternative derivation based on the

DOS and group velocity can be found in previous studies.

13,14

We will focus on

difﬁculty of (i) making transparent contacts to semiconducting nanotubes and (ii) fabricating

small channel lengths.

K. Natori, Y. Kimura and T. Shimizu, Characteristics of a carbon nanotube ﬁeld-effect transistor

analyzed as a ballistic nanowire ﬁeld-effect transistor. J. Appl. Phys., 97 (2005) 034306.

D. Akinwande, J. Liang, S. Chang, Y. Nishi and H.-S. P. Wong, Analytical ballistic theory of

carbon nanotube transistors: experimental validation, device physics, parameter extraction, and

performance projections. J. Appl. Phys., 104 (2008) 124514.

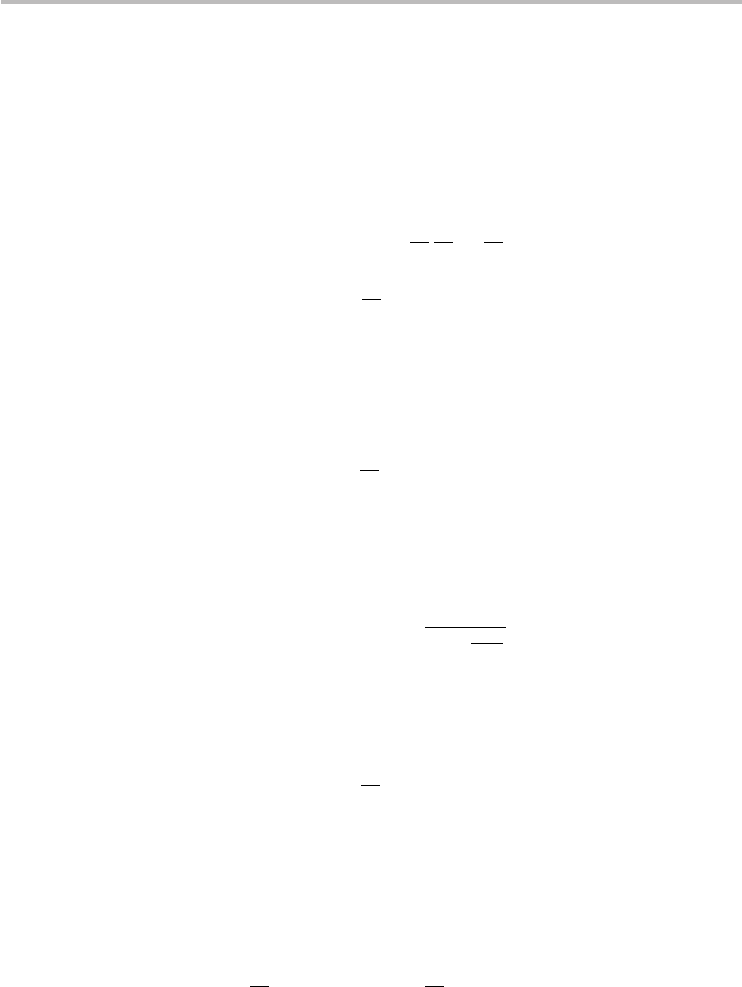
202 Chapter 8 Carbon nanotube ﬁeld-effect transistors

the n-type transistor (or n-CNFET for short) operation, where the contributions of

holes are considered negligible. The ﬁnal results apply equally to p-CNFETs as

well. Planck’s quantum postulate relating the energy of the ith state to its frequency

can be explicitly rewritten in terms of the current from the particles occupying the

ith state:

= hf

, (8.14)

, (8.15)

where f

and τ

are respectively the frequency and period of particles in the ith state.

For a system containing many states, the total current is the sum of the energy of

each state and the associated probability of occupation of the state:

I =



F(E

, E

, (8.16)

where F(E, E

) is the Fermi–Dirac statistic describing the probability that a state

with energy E is occupied by electrons and E

is the equilibrium Fermi energy:

F(E, E

) =

1 + e

E−E

. (8.17)

In the limit that the states are very dense (i.e. the spacing between the discrete

states becomes negligible), the sum can be converted to a Riemann integral:

I =



F(E, E

) dE. (8.18)

In CNTs, there are right-moving carriers (electrons with positive velocities) and

left-moving carriers (electrons with negative velocities); hence, the net current

(commonly known as the drain current I

) is the difference between the right- and

left-moving carriers:



dEF(E, E

) −



dEF(E, E

− eV

). (8.19)

The Fermi energy of the right-moving carriers is controlled by the source potential,

while that of the left-moving carriers is controlled by the drain potential. We set

the source potential to 0 V for reference and, as such, for a positive drain voltage,

at the drain electrode will be correspondingly pulled down (see Figure 8.4b for

a visual illustration). Including the contributions of all the subbands in a semicon-

ducting nanotube, the total drain current becomes the sum of the net current from

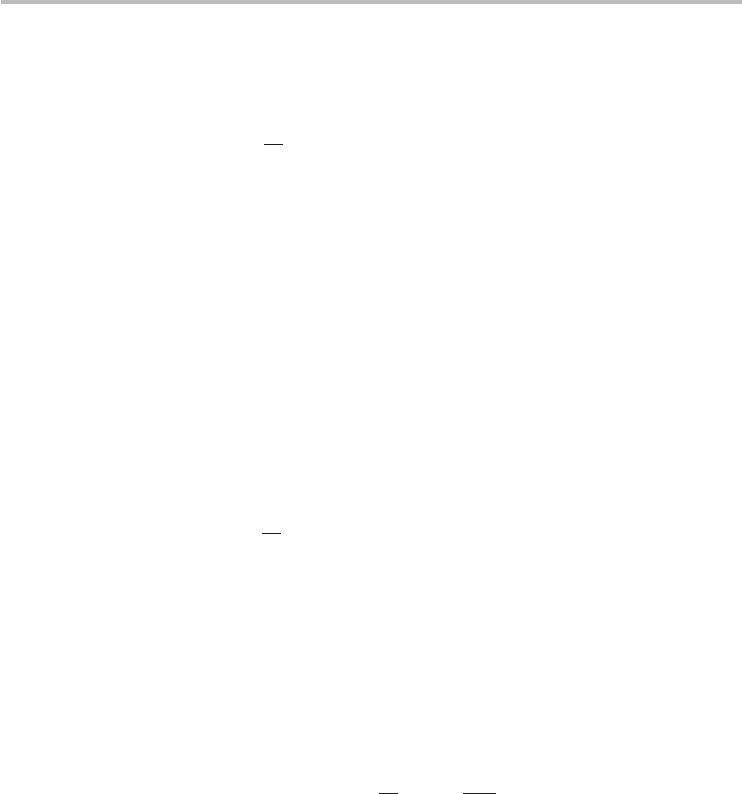
8.4 Ballistic theory of ohmic-contact CNFETs 203

each subband:

D,tot



∞



−eϕ

dE [F(E, E

) − F(E, E

− eV

)], (8.20)

where j is the subband index and E

is the energy minimum or bottom of the jth-

subband (for reference, E

for the ﬁrst two subbands are shown in Figure 8.2). In

general, Eq. (8.20) is computed by numerical integration for the transistor drain

current. Fortunately, as a result of the analytical surface potential developed in

the previous section, we can obtain a simpliﬁed closed-form expression for the

drain current. The surface potential appropriate for a three-terminal device such

as a transistor will be elucidated towards the end of this section. At low operating

voltages characteristic of nanoscale technologies (supply voltages are typically

≤1 V), higher subbands can be ignored with negligible effect and Eq. (8.20),

therefore, simpliﬁes to the contribution of the ﬁrst subband.

∞



−eϕ

[

F(E, E

) − F(E, E

− eV

)

]

. (8.21)

The additional factor of 2 in the preﬁx is due to the ﬁrst subband degeneracy. It

follows that the integral yields an analytic formula for the drain current:

= I

1 + e

2eϕ

−E

/2k

− ln

1 + e

2eϕ

−2eV

−E

/2k

, (8.22)

where I

T =

, (8.23)

with R

representing the usual quantum resistance (R

= h/4e

∼ 6.45 k). At

300 K, I

∼ 4 µA. Equation (8.22) is the essential low-energy ballistic I−V for a

CNFET with transparent contacts as a function of the terminal voltages, material

properties, and temperature.

Let us take a moment to contemplate on the functional dependencies in the

formula and interpret its form. k

T comes about in the expression courtesy of

the thermodynamic Fermi–Dirac distribution, R

reﬂects the quantum transport of

carriers, and E

reﬂects the bandgap dependence. ϕ

captures the band structure of

the material (vis-à-vis the quantum capacitance) and also the effect of the external

Furthermore, Guo and coworkers have shown by computation (for an intrinsic ballistic CNFET)

that the ﬁrst subband largely determines current under low-bias conditions. See J. Guo, A. Javey,

H. Dai and M. Lundstrom, Performance analysis and design optimization of near ballistic carbon

nanotube ﬁeld-effect transistors. IEEE IEDM Tech. Digest, (2004) 703–6.

204 Chapter 8 Carbon nanotube ﬁeld-effect transistors

gate voltage in controlling the channel charge. V

is the other external inﬂuence

by which charge transport can be controlled. The ﬁrst term is the current from the

right-moving carriers, while the latter term is due to the left-moving carriers. An

important observation is that the current from the backward carriers is signiﬁcant

in the linear region of the transistor I

−V

. The current from the forward carriers

determines the saturation current, also known as the ON current I

, because at

high V

the latter term becomes negligible and the current saturates independent of

. We can obtain a rough estimate for the maximum I

by reasonably assuming

that the maximum surface potential (in the low-energy ballistic regime) is slightly

greater than the energy minima of the ﬁrst subband, say eϕ

∼ 1.5E

= 0.75E

In this case, for d

from 1–3 nm at room temperature, the maximum ﬁrst subband

is within a factor of 2 of 24 µA. For a p-CNFET, Eq. (8.22) is modiﬁed by

reversing the polarity of ϕ

and V

= I

1 + e

−(2eϕ

)/2k

− ln

1 + e

(2eV

−2eϕ

−E

)/2k

. (8.24)

The surface potential appropriate for a three-terminal device such as the CNFET

is slightly different from Eq. (8.1) deﬁned in the previous section, which was

based on a two-terminal device structure where the source and drain are shorted

together. For the two-terminal device all the induced charges effectively travel

in the same direction, leading to a displacement current, and the purpose of the

surface potential is to account for all the induced charges in the nanotube. For the

case of a three-terminal device such as the n-type CNFET, at equilibrium, half

of the mobile electrons are right-moving carriers and the remaining half are left-

moving carriers. Hence, the appropriate surface potential to be used for a CNFET

(Eqs. (8.22)or(8.24)) must account for the charge carriers per direction in the

nanotube. That is, for example, the surface potential in the ﬁrst or latter term of

Eq. (8.22) should account for only half of the induced charges, since those are the

charges moving with positive or negative velocities respectively. In this case, the

proper deﬁnition for the surface potential for CNFETs is

(ϕ

)

+ C

(ϕ

)

(8.25)

where the factor of 2 represents the fact that only half the charges are traveling in

any particular direction at any gate voltage with V

= 0. This is, of course, similar

to Eq. (8.1); as such, the analytical expression developed for the surface potential

(Eq. (8.13)) can still be employed with C

replaced with 2C

in the expressions

for the model parameters, s and t. Under excitation, the role of a ﬁnite V

is to

suppress the backward carriers in a CNFET.

An additional concern that needs to be incorporated in a general formulation

for the surface potential is the ﬂatband voltage V

All along we have been

In a nutshell, the ﬂatband voltage is the voltage applied to the gate to get a ﬂat energy band

diagram along the vertical cross-section of the device, and is given by V

= 

where 

8.4 Ballistic theory of ohmic-contact CNFETs 205

=f (ϕ

)

–

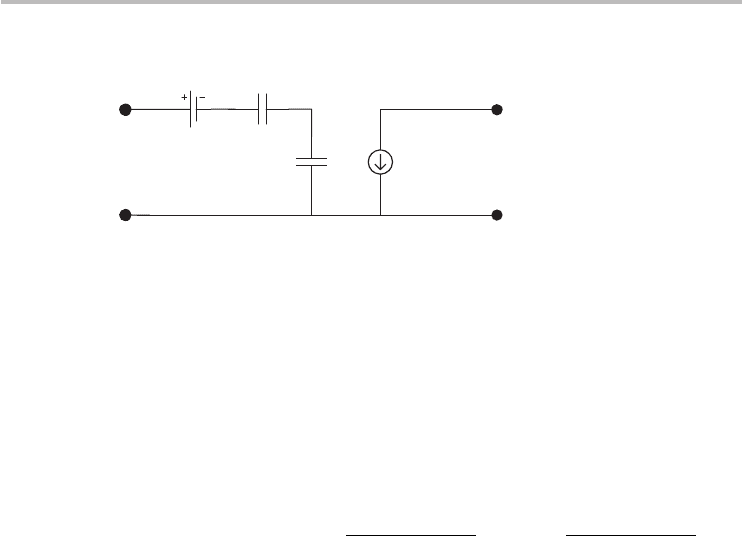
Fig. 8.5 An electrostatic intrinsic circuit model of the ballistic CNFET.

using V

assuming ﬂatband conditions at V

= 0 V. In general, inclusion of the

workfunction difference between the gate metal and the nanotube leads to

= V



+ V

, (8.26)

where V



is the voltage under ﬂatband conditions. The expression for V



should

be used in the formula for the surface potential:

(

− V

)



1 −



1 −

s|V

− V

|+t





1 −

s|V

− V

|+t



(8.27)

For a non-zero voltage at the source electrode, V

and V

should be used instead

of V

and V

respectively in the expressions for the drain current and surface

potential. An intrinsic electrostatic (sometimes called large-signal) circuit model

of the ballistic CNFET is shown in Figure 8.5.

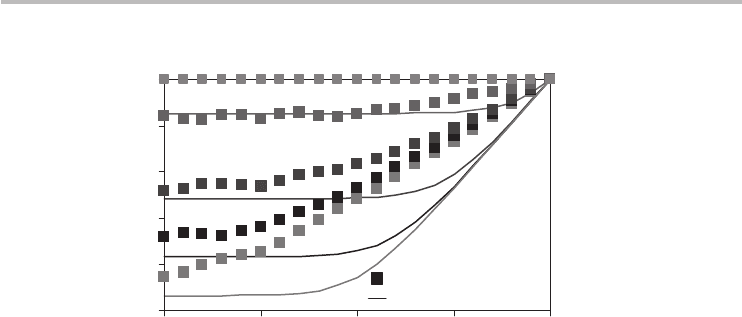
The value of analytical theories depends on how successfully the theory corrob-

orates experimental observations. For this purpose, the analytical ballistic theory,

Eq. (8.24), is compared in Figure 8.6 with an experimental ballistic p-CNFET

reported by Javey et al.

The model parameters used are identical to the values

reported for the experimental CNFET (d

= 1.7 nm, E

= 0.5 eV, and device

geometry shown in Figure 8.4b), including a parasitic source/drain metal resis-

tance of 2 k each, which is close to the reported estimate of ∼1.7 k. Parameter

extraction of the ﬂatband voltage from the experimental data yielded a value of

∼ 0.28Vwhich is used in the comparison.

Amodest agreement is observable

in the active or current saturation region, while in the linear region the analytical

ballistic theory signiﬁcantly overestimates the current and conductance. The origin

of the discrepancy can be identiﬁed upon closer examination of the band diagrams

in Figure 8.4, and is elaborated upon in the next section.

the workfunction difference between the gate and the semiconductor. Basically, for a positive or

negative V

the action of the gate is retarded or enhanced respectively in an n-CNFET, and vice

versa for a p-CNFET. Enhancement (retardation) implies less (more) voltage is needed to turn ON

the device.

A. Javey, J. Guo, D. B. Farmer, Q. Wang, E. Yenilmez, R. G. Gordon, et al., Self-aligned ballistic

molecular transistors and electrically parallel nanotube arrays. Nano Lett., 4 (2004) 1319–22.

206 Chapter 8 Carbon nanotube ﬁeld-effect transistors

–25

–20

–15

–10

–5

–0.4 –0.3 –0.2 –0.1 0

(V)

from 0.2 to –1 V

–0.3 V steps

Experimental (A. Javey)

Analytical ballistic theory

(µA)

Fig. 8.6

Experimental results and analytical model predictions, Eq. (8.24), for a ballistic 50 nm

p-type CNFET (identical to Figure 8.4b). s = 1.6 and t = 0.82 for the analytical φ

Agreement is good in the active region but weak in the linear region due to optical phonon

scattering, which needs to be accounted for in the theory. (Experimental results are

courtesy of Javey et al.

)

8.5 Ballistic theory of CNFETs including drain optical

phonon scattering

So far we have found the ballistic theory of CNFETs to be in modest agreement

with experimental data in the current saturation or active region of the I −V curve.

However, a signiﬁcant discrepancy exists in the linear region. A closer scrutiny of

the band diagram of the ballistic CNFET proves useful in providing guidance as to

the way forward to an improved theory. Figure 8.7 illustrates the conduction band

diagram of an n-CNFET under two drain bias conditions. Figure 8.7aisatalow

drain bias corresponding to the linear region, while Figure 8.7b corresponds to the

saturation region. Wecan see visually that otherwise low-energyelectrons traveling

through the channel towards the drain will acquire signiﬁcant energy at the drain

end of the channel.

This forces us to re-examine our assumption of ballisticity.

While it is true that electron transport through most of the channel is ballistic (a ﬂat

band signiﬁes a ballistic channel without resistive voltage drop), at the drain end

the prospect of optical phonon scattering characteristic of high-energy particles is

certainly possible. In CNTs, the criteria to be satisﬁed for electron scattering by

optical phonons is that (i) the length of travel through the well l

, (see Figure 8.7)

should be greater than the optical phonon mean free path (l

∼ 10 nm) and (ii) the

energy of the electrons must be greater than the critical optical phonon emission

The kinetic energy of the electrons is the excess energy acquired beyond the conduction band

energy minima.

8.5 Ballistic theory of CNFETs 207

< V

> l

Significant optical

phonon scattering

Negligible optical

phonon scattering

(a)

(b)

Fig. 8.7

Illustration of optical phonon scattering in a ballistic (n-type) CNFET. (a) At low V

, the

length of the triangle-like well l

is comparable to the mean free path of optical phonon

scattering (l

∼ 10 nm), thereby reducing I

. (b) At higher V

, the well is sharpened,

becoming gradually less than l

and, hence, having a minimal effect on I

. This device

physics can be captured to ﬁrst-order by the DOPS parameter α, which accounts for the

reduced current.

energy (E

∼ 0.16 eV; see Chapter 7). If these conditions are satisﬁed,

then

optical phonon scattering will occur at the drain end of the channel and, hence, the

current (and conductance) in the linear region will be reduced accordingly, cor-

roborating experimental observations. At higher drain bias (saturation region), the

triangular well becomes steeper,

with an ever-decreasing length, which implies

that electron scattering by optical phonons becomes negligible as l

< l

, leading

to minimal correction of the ballistic theory in the active region.

The scattering of high-energy electrons by optical phonons in an otherwise

ballistic channel can be incorporated into the ballistic theory by a phenomenolog-

ical parameter which is rightly called the drain optical phonon scattering (DOPS)

parameter α. The justiﬁcation of this parameter is as follows. Optical phonon

scattering at the drain end essentially implies a localized resistance leading to an

effective drain voltage across the ballistic portion of the channel that is less than

the terminal drain voltage. In this light, we can construct a DOPS parameter to

quantify the effective or reduced drain voltage. It follows that the effective drain

voltage can be written phenomenologically as αV

where 0 <α≤ 1, leading to

a more realistic expression for the drain current:

= I

1 + e

(±2eϕ

−E

)/2k

− ln

1 + e

(±2eϕ

∓2eαV

−E

)/2k

(8.28)

It can be shown that the conditions can be satisﬁed in the linear region of the I −V by employing

semiconductor junction theory.

In semiconductor device physics, the potential well is often considered a carrier depletion region

and modeled as a capacitance. At higher drain voltages, the electrostatic attraction is greater,

thereby pulling the electrons closer to the drain side, resulting in a steeper potential well.

208 Chapter 8 Carbon nanotube ﬁeld-effect transistors

–25.00

–20.00

–15.00

–10.00

–5.00

0.00

–0.4 –0.3 –0.2 –0.1 0

(V) V

(V)

from 0.2 to –1 V

–0.3 V steps

Experimental (A. Javey)

Computation (J. Guo)

Analytical ballistic theory

(µA)

–1 –0.8 –0.6 –0.4 –0.2 0 0.2

–4

–5

–6

–7

–8

–9

–I

(A)

Experimental (A. Javey)

Analytical ballistic theory

Analytical (C

metallic

)

= –0.3 V

= –0.1V

(a) (b)

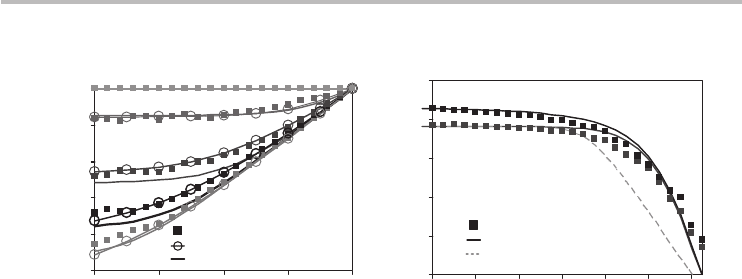
Fig. 8.8 (a) I

−V

including the DOPS parameter (α = 0.5) showing strong agreement between

analytical ballistic theory Eq. (8.28), experimental results, and quantum mechanical

computation. (b) Likewise, I

− V

also results in strong agreement with experimental

data in active, linear, and sub-threshold regions. The dashed line (V

=−0.1 V) is the

analytical prediction if C

= C

q,metallic

is assumed, as is sometimes employed in compact

modeling of semiconducting CNTs, leading to gross errors in the sub-threshold and active

regions but which is fairly accurate in the linear region. (Experimental and quantum

mechanicalcomputationdataarecourtesyofA.Javey,J.Guo,etal.

)

where the upper polarity is for n-CNFETs and the lower polarity is for p-CNFETs.

In general, α should depend on both the gate and drain voltages, since they con-

trol the length and energy of the triangular well. For the greatest simplicity, let us

consider the DOPS parameter a constant which is extractable from experimental

data.

Returning to the experimental data of Javey et al.,

the maximum channel

conductance value of ∼0.5/R

was reported corresponding to α ∼ 0.5. Employing

this value of α, we observe that the DOPS-corrected ballistic current, Eq. (8.28),

is justiﬁed by the remarkably strong agreement with the experimental data in all

major regions of transistor operation (sub-threshold, linear, and saturation), as

shown in Figure 8.8. Detailed self-consistent quantum mechanical computations

reportedbyJ.Guofortheexperimentaldevicearealsoincludedforreference,

demonstrating the strength of the analytical ballistic theory in accurately repro-

ducing the experimental and quantum mechanical results. The slight disagreement

in the OFF state (V

∼ 0.2 V in Figure 8.8b) is due to ambipolar electron current,

which can be handled within the Schottky-barrier CNFET model developed in

Section 8.8.

In order to provide clarity in the use of the term ballistic transport in transistors,

it is necessary to make two distinctions:

(i) Fully ballistic transport:This isdeﬁned as transport with no acoustic or optical

phonon scattering (α = 1).

The DOPS parameter α can be extracted from measurements of the drain to source channel

conductance (g

), in the limit of V

→ 0, and V

→ V

where V

is the drain supply

voltage. In this limit, the conductance is g

= α/R