Weinan E. Principles of Multiscale Modeling
Подождите немного. Документ загружается.

3.6. NOTES 137
In addition to sparsity and orthonormal wavelets, redundancy and the associated
concept of tight frames have also been studied (see, e.g. [35]). It has been discovered
that redundancy can often provide the needed flexibility in order to tune to the specific
features of the particular application that one has to deal with.
3.6 Notes
This chapter is admittedly very terse, for a good reason: A lot has been written on
the topics discussed here. Thorough discussions of the topics reviewed here can be found
in various textbooks and review articles listed at the end of the chapter. We find it
useful to include at least a brief discussion of the main ideas in these classical multiscale
algorithms for several reasons:
1. These ideas are the basic building blocks for multiscale algorithms.
2. This discussion makes it easier for us to see the difference between the philosophy
behind these classical algorithms and the new ones to be presented later.
There are many linear scaling, multiscale algorithms that we did not cover in this
chapter. Obvious examples include: the H-matrix techniques [10], other analysis-based
fast transforms, algorithms based on discrete symbol calculus [19], etc.
138 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS
Bibliography
[1] M. Ainsworth and J. T. Oden, A Posteriori Error Estimation in Finite Element
Analysis, John Wiley, New York, 2000.
[2] A. W. Appel, “An efficient progam for many-body simulation,” SIAM. J. Sci. Stat.
Comput., vol. 6, pp. 85–103, 1985.
[3] I. Babuska and W. C. Rheinboldt, “Error estimates for adaptive finite element com-
putations,” SIAM J. Numer. Anal., vol. 18, pp. 736–754, 1978.
[4] I. Babuska and W. C. Rheinboldt, “A posteriori error estimates for the finite element
method,” Internat. J. Numer. Methods Engng., vol. 12, pp. 1597–1615, 1978.
[5] R. E. Bank and A. Weiser, “Some a posteriori error estimators for elliptic partial
differential equations,” Math. Comp., vol. 44, 283–301, 1985.
[6] J. Barnes and P. Hut, “A hierarchical O(N log N) force-calculation algorithm,” Na-
ture, vol. 324, pp. 446–449, 1986.
[7] R. Beatson and L. Greengard, “A short course on fast multipole methods,” Wavelets,
Multilevel Methods and Elliptic PDEs, (M. Ainsworth, J. Levesley, W. Light, and
M. Marletta, eds.), pp. 1-37, Oxford University Press, 1997.
[8] M. J. Berger, and P. Collela, “Local adaptive mesh refinement for sho ck hydrody-
namics,” Journal of Computational Physics, vol. 82, no. 1, pp. 64–84, 1989.
[9] G. Beylkin, R. Coifman and V. Rokhlin, “Fast wavelet transforms and numerical
analysis,” Comm. Pure Appl. Math., vol. 44, no. 2, pp . 141–183, 1991.
[10] S. B¨orm, L. Grasedyck, and W. Hackbusch, Hierarchical Matrices, Max-Planck-
Institute Lecture Notes, 2006.
139
140 BIBLIOGRAPHY
[11] A. Brandt, “Multi-level adaptive solutions to boundary value problems,” Math.
Comp., vol. 31, no. 138, pp. 333–390, 1977.
[12] A. Brandt, “Multiscale scientific computation: review 2001,” Multiscale and Mul-
tiresolution Methods: Theory and Applications, Yosemite Educational Symposium
Conf. Proc., 2000, Lecture Notes in Comp. Sci. and Engrg., T.J. Barth, et.al (eds.),
vol. 20, pp. 3–96, Springer-Verlag, 2002.
[13] W. L. Briggs, V. E. Henson and S. F. McCormick, A Multigrid Tutorial, SIAM
Publications, 2nd ed., 2000.
[14] D. A. Caughey and A. Jameson, “Fast preconditioned multigrid solution of th e
Euler and Navier-Stokes equations for steady compressible flows,” International J.
for Numerical Methods in Fluids, vol. 43, pp. 537–553, 2003.
[15] S. D. Conte and C. de Boor, Elementary Numerical Analysis, McGraw-Hill, 1980.
[16] I. Daubechies, Ten Lectures on Wavelets, SIAM, 1992.
[17] S. F. Davis and J. E. Flaherty, “An adaptive finite element method for initial bound-
ary value problems for partial differential equations,” SIAM J. Scientific and Sta-
tistical Computing, vol. 3, pp. 6–27, 1982.
[18] C. de Boor, R.A. DeVore and A. Ron, “Approximation from shift-invariant subspaces
of L
2
(R
d
)”, Transactions of the American Mathematical Society, vol. 341, No. 2, pp.
787–806, 1994.
[19] L. Demanet and L. Ying, “Discrete symbol calculus,” preprint.
[20] P. Deuflhard and A. Hohmann, Numerical Analysis in Modern Scientific Computing:
An Introduction, Springer, 2000.
[21] W. E, M. Mu and H. Huang, “A posteriori error estimates for finite element meth-
ods,” Chinese Quarterly Journal of Mathematics, vol. 3, pp. 97–106, 1988.
[22] R.P. Fedorenko, “Iterative methods for elliptic difference equations,” Russian Math-
ematical Surveys, vol. 28, pp. 129–195, 1973.
BIBLIOGRAPHY 141
[23] A. L. Garcia, J.B. Bell, W.Y. Crutchfield and B.J. Alder “Adaptive mesh and algo-
rithm refinement using direct simulation Monte Carlo,” J. Comput. Phys., vol. 154,
pp. 134–155, 1999.
[24] J. Goodman and A. D. Sokal, “Multigrid Monte Carlo methods,” Phys. Rev. D, vol.
40, no. 6, pp. 2035–2071, 1989.
[25] L. Greengard and V. Rokhlin, “A fast algorithm for particle simulations,” J. Comput.
Phys., vol. 73, pp. 325, 1987.
[26] L. Greengard and J. Strain, “The fast Gauss transform,” SIAM J. Sci. Stat. Comput.
vol. 12, pp. 79–94, 1991.
[27] W. Hackbusch, “Convergence of multigrid iterations applied to difference equations,”
Math. Comp., vol. 34, no. 150, pp. 425–440, 1980.
[28] W. Hackbusch, “A sparse matrix arithmetic based on H-matrices. Part I: Introduc-
tion to H-matrices,” Computing, vol. 62, pp. 89–108, 1999.
[29] R. Li, T. Tang and P. Zhang, “Moving mesh metho ds in multiple dimensions based
harmonic maps,” J. Comput. Phys., vol. 170, pp. 562–588, 2001.
[30] S. Mallat, “Multiresolution approximation and wavelets,” Trans. Amer. Math. Soc.,
vol. 315, pp. 69–88, 1989.
[31] S. Mallat, “A theory for multiresolution signal decomposition: the wavelet represen-
tation,” IEEE Trans. PAMI, vol. 11, pp. 674–693, 1989.
[32] K. Miller and R. N. Miller, “Moving finite element. I,” SIAM J. Numer. Anal., vol.
18, pp. 1019–1032, 1981.
[33] Y. Ren and R. D. Russell, “Moving mesh techniques based upon equidistribution
and their stability,” SIAM J. Scientific and Statistical Computing, vol. 13, pp. 1265–
1286, 1992.
[34] W. Ren and X. Wang, “An iterative grid redistribution method for singular problems
in multiple dimensions,” J. Comput. Phys., vol. 159, pp. 246–273, 2000.
142 BIBLIOGRAPHY
[35] Z. Shen, “Wavelet frames and image restorations”, Proceedings of the International
Congress of Mathematicians, Hyderabad, India, 2010.
[36] G. Strang and G. Fix, “A Fourier analysis of the finite element variational method”,
C.I.M.E. II Ciclo 1971, in Constructive Aspects of Functional Analysis, G. Geymonat
ed., 793-840, 1973.
[37] A. Toselli and O. Widlund, Domain Decomposition Methods, Springer, 2004.
[38] R. Verf¨urth, “A posteriori error estimators for the Stokes equations,” Numer. Math.,
vol. 55, pp. 309–325, 1989.
[39] A. M. Winslow, “Numerical solution of the quasilinear poisson equation in a nonuni-
form triangle mesh,” J. Comput. Phys., vol. 1, pp. 149–172, 1967.
[40] W. Yang and T.-S. Lee, “A d ensity-matrix divide-and-conquer approach for elec-
tronic structure calculations of large molecules,” J. of Chem. Phys., vol. 103, no. 13,
pp. 5674–5678, 1995.
[41] D. Young and L. A. Hageman, A pplied Iterative Methods, Dover Publications, 2004.
[42] H. Yserentant, “On the multi-level splitting of finite element spaces,” Numer. Math.,
vol. 49, pp. 379–412, 1986.
[43] O. C. Zienkiewicz and J. Z. Zhu, “A simple error estimator and adaptive procedure
for pr actical engineering analysis,” Internat. J. N umer. Methods Engrg., vol. 24, pp.
337–357, 1987.
Chapter 4
The H ierarchy of Physical Models
Given a physical system, we can model it at different levels of detail. This results in
a hierarchy of physical models, each of which is a refinement of the models at the higher
levels of the hierarchy (see Table 1.2.3). For example, if we want t o model the dynamics
of gases, we have the following options to choose from:
1. Continuum mechanics, the Euler and Navier-Stokes equations.
2. Kinetic theory, the Boltzmann equation.
3. Molecular dynamics, the Newton’s equation.
4. Quantum mechanics, the Schr¨odinger equation.
Continuum mechanics models, such as the Euler’s equation and the Navier-Stokes equa-
tion, are the crudest in this hierarchy. They mo d el only the macrosopic density, velocity
and temperature fields of the gas. Nevertheless, they are already quite sufficient in many
engineering applications. Quantum mechanics models are the most detailed ones. They
are required if we are interested in the details of the collision process between gas parti-
cles. Kinetic theory and molecular dynamics models are of the intermediate complexity,
capturing respectively the phase space probability distribution and the phase space dy-
namics of the gas particles.
Of course inside each level of this hierarchy, there are sub-hierarchies, i.e. models
of different complexity and detail. For example, at the level of the quantum mechanics
models for electronic structure analysis, we have:
143
144 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
1. Orbital-free density functional theory, such as the Thomas-Fermi-von Weizs¨acker
(TFW) model.
2. Kohn-Sham density functional theory.
3. The full quantum many-body problem.
The TFW model uses only the electron density to describ e the electronic structure of the
system. Kohn-Sham density functional theory uses a set of (fictitious) one-body wave
functions. The full quantum many-body problem is the true first principle. It describes
an electronic system at the level of the many-body wave function.
Since they all describe the same physical system, the different models have to produce
consistent resu lts. Understanding this analytically is one of the main tasks in multiscale
modeling. For example, one should be able to derive Euler’s equation of gas dynamics
from molecular dynamics models in the regime where Euler’s equation is supposed to be
valid. Among other things, this d erivation should provide us a microscopic expression
for the constitutive relations in Euler’s equation.
In this chapter, we will discuss the essential components of these models. We will
start at the top of the hierarchy, the continuum mechanics models. This is followed by
the classical atomistic models in the form of molecular dynamics. We then introduce the
basic ingredients of kinetic theory, which at least for gases serves as the bridge between
the many-body molecular dynamics models and the continuum mechanics models. We
will end this chapter at the bottom of the hierarchy, the quantum mechanics models. This
chapter is certainly not going to be an exhaustive treatment of the different physical laws
used in modeling. Bu t we hope to convey the basic ideas.
4.1 Continuum mechanics
In continuum mechanics, the system of interest is treated as a continuous media. The
basic objects that we study are in the form of fields, such as the velocity and density fields.
In th is section, we will discuss the basic ideas needed in order to formulate continuum
models. We b egin by introducing the basic concepts in kinematics, namely the concepts
of stress and strain or the rate of strain. We then discuss nonlinear elasticity models of
solids. F inally, we discuss dynamic models of solids and fluids.
4.1. CONTINUUM MECHANICS 145
x
y
Undeformed
deformed
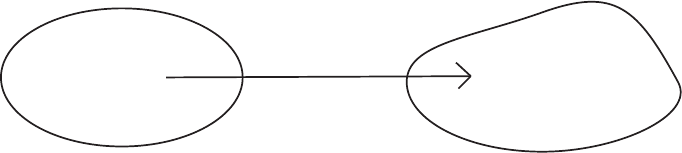
Figure 4.1: The L agrangian and Eulerian coordinates of a continuous media: x represents
the Lagrangian coordinates, y represents the Eulerian coordinates.
To describe these fields, we need a coordinate system. The most commonly used
coordinate systems are the Lagrangian coordinates and the Eulerian coordinates. In
Lagrangian coordinates, a point in the system is described by its initial position, or the
position in a fixed reference frame which in solids is usually the undeformed configuration.
In Eulerian coordinates, a point in the system is described by its current position, after
the system has changed as a result of deformation or flow. In Figure 4.1, x denotes
the Lagrangian coordinates and y denotes the Eulerian coordinates. The mapping from
x to y is called the L agrangian to Eulerian map. Its inverse is called the Eulerian to
Lagrangian map. One main difference between solid and fluid mechanics is that models
in solid mechanics such as elasticity theory typically use the Lagrangian coordinates,
whereas in fluid mechanics, we typically use the Eulerian coordinates. One reason is
that in fluids, the deformation can be so large that it does not make much sense to refer
back to the initial position of the material point. This difference creates some problems
when modeling systems whose behavior is intermediate between fluids and solids, such
as visco-elastic fluids or plastically deformed solids.
Continuum theory is often divided into two related parts: statics and dynamics. Mod-
els for statics are generally in the form of variational principles, asserting, for example,
that the static configuration of a material minimizes the total free energy of the system
taking into account the work done by external forces. Dynamic models are generally in
the form of dynamic conservation laws of mass, momentum and energy.
A central concept in treating the continuous media is the stress. It describes the
forces acting on (virtual) surfaces inside the medium. Imagine an infinitesimally small
146 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
piece of surface placed inside a continuous medium. As a consequence of the short-ranged
molecular interaction, there is a force between the material on one side of the surface
and the material on the other side of the surface. This force is called the stress. It is
the macroscopic manifestation of the microscopic, short-range interaction between the
atoms on the two sides of the surface. The long-range interactions, such as the Coulomb
interaction, are usually represented as body force. It is easy to see that stress depends
linearly on the orientation of the surface. At each point of the medium, it is a mapping
between the orientation of the surface and the force that we just described. Therefore it
is a rank-2 tensor.
To obtain a closed model, we have to express stress in terms of the displacement
field, including its derivatives. This is the role played by the constitutive relation. The
following are some examples of constitutive relations:
1. Equation of state for gases.
2. Stored energy density for solids.
3. Stress-strain relation for solids.
4. Stress as a function of the rate of strain for fluids.
Constitutive relations are the macroscopic representation of the nature of the microscopic
constituents of the system, i.e., the atoms that make up the system. This is where
most of the empirical modeling in continuum theory comes in. For simple systems,
linear constitutive relations have been remarkably successful. In fact, in many cases,
constitutive modeling proceeds by [12]:
1. Writing down linear relations between the generalized forces and the generalized
fluxes.
2. Using symmetry properties to reduce the number of independent coefficients.
These coefficients, for example the elastic moduli or the viscosity coefficients, can then
be measured experimentally. From an abstract viewpoint, the only constraints on these
coefficients are the second law of thermodynamics and the symmetry of the system.
In fact, non-equilibrium thermodynamics, a subject that has had a lot of success after
the work of Onsager, Prigogine, etc, was created to treat general systems using these
principles [12].
