Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

3.5. MULTISCALE REPRESENTATION 127

3.5 Multiscale representation

To ﬁnd the solution to any physical model, ﬁrst we have to have a way of representing

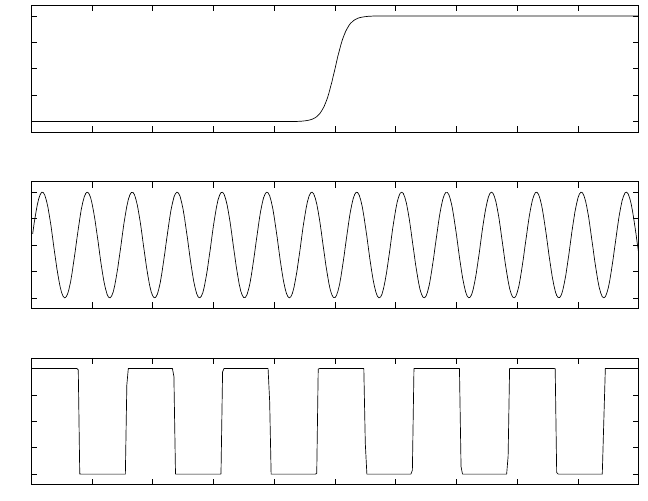
the solution. Consider the three examples of functions shown in Figure 3.8. The ﬁrst

example has a near discontinuity but the near discontinuity is isolated. The second

example shows a repetitive pattern which in this case happen to be periodic.

It is intuitively quite clear that localized bases such as wavelet bases are suited for

the ﬁrst example; periodic bases such as the Fourier bases are suited for the second

example. It is not quite clear what to do about the third example. Clearly, if we restrict

ourselves to the Fourier and wavelet representations, then the relative eﬃciency of the

two depends on the amplitude of the large gradients and the frequency of the oscillations:

If we use a Fourier representation, then the number of Fourier coeﬃcients needed in order

to achieve a particular accuracy depends strongly on the size of the large gradient, but

only weakly on the frequency. If we use a wavelet representation, then the number of

wavelet coeﬃcients needed in ord er to achieve a particular accuracy depends linearly on

the frequency, but only weakly on the size of the gradient.

These simple examples illustrate the kind of multiscale behavior that we need to

consider. In particular, the repetitive pattern displayed in the second and third examples

is in some ways quite representative of the situation with scale separation, when the

macroscale of th e system is much larger than the microscale. In this case, the local

microstructure is repetitive in some pointwise or statistical sense.

3.5.1 Hierarchical bases

Consider a partition of the unit interval Ω = [0, 1] into N = 2

subintervals of equal

length and consider the piecewise linear ﬁnite element space over this partition with

Dirichlet boundary condition:

= {v

: v

is continuous, piecewise linear, and v

(0) = v

(1) = 0} (3.5.1)

Denote the nodes in this partition by {x

}, j = 1, ··· , N − 1, x

= jh, h = 1/N. In

standard ﬁnite element methods, we use the nodal basis to represent functions in the

space V

. These are functions {φ

} in V

that satisfy:

) = δ

, j, k = 1, 2, ··· , N − 1 (3.5.2)

128 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−1

−0.5

0.5

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−1

−0.5

0.5

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−1

−0.5

0.5

Figure 3.8: Three diﬀerent kinds of multiscale functions

3.5. MULTISCALE REPRESENTATION 129

This basis has the advantage that for any function v

in V

, the coeﬃcients in the

expansion of v

in terms of this nodal basis are simply the values of v

at the nodes:

(x) =

N−1

(x), c

= v

) (3.5.3)

However, it also has the disadvantage that the condition number of the stiﬀness matrix

for the ﬁnite element method, deﬁned as

= (a

), a

(x)Lφ

(x)dx (3.5.4)

for an operator L, is usually very large. Recall that the condition number of a matrix A is

deﬁned as κ(A) = kAkkA

−1

k if the norm k·k is used to measure the vectors. For example,

if L is a second order elliptic diﬀerential operator L, then typically κ(A

) ∼ O(h

−2

). This

is an important issue since the condition number controls the accuracy and eﬃciency of

the algorithms in numerical linear algebra [20] (see also Section 3.1).

0 1

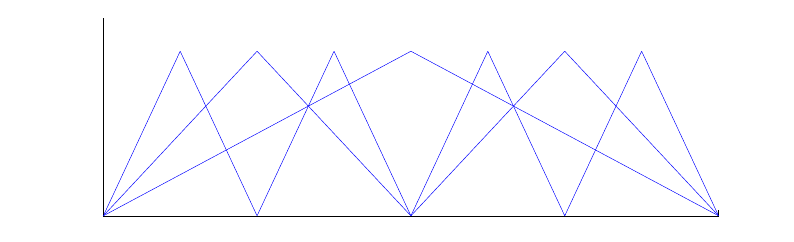
Figure 3.9: Illustration of hierarchical basis functions (courtesy of Xiang Zhou).

This bad scaling behavior of κ(A

) is partly due to the locality of the nodal basis

functions. An alternative basis set, the hierachical basis, was suggested and analyzed by

Yserentant [42], and is shown schematically in Figure 3.9. One advantage of this basis is

that the condition number of the associated stiﬀness matrix is of O(1).

When hierachical basis are used to represent functions in the ﬁnite element space,

the coeﬃcients are no longer simply the values at the nodes or vertices. However, due to

the hierachical nature of the basis, eﬃcient hierachical algorithms can be constructed to

compute these coeﬃcients [42].

130 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

Hierachical basis can be constructed for ﬁnite element spaces in high dimensions [42].

The condition number of the stiﬀness matrix in high dimension is no longer of O(1).

For example, in two dimension, the condition number scales as O(|log h|

), which is still

much better than the O(h

−2

) scaling for the nodal basis.

3.5.2 Multi-resolution analysis and wavelet bases

In a multi-resolution analysis (MRA), we consider a sequence of nested subspaces

of the ambient space (say L

(R)), {V

, j ∈ Z}, where roughly speaking, V

contains

functions with components upto the j-th scale. The precise requirement for this ladder of

subspaces is formalized by S. Mallat [30, 31]. The sequence of subspaces {V

}

j∈Z

⊂ L

(R)

is an MRA if the following holds:

1. V

⊂ V

j+1

, j ∈ Z;

2. V

is the scaled version of V

: f (x) ∈ V

if and only if f(2

x) ∈ V

;

j∈Z

= {0},

j∈Z

= L

(R);

4. There exists a function φ such that the integer translations {φ(· − n), n ∈ Z}

constitutes an orthonormal basis for V

Consequently, if we deﬁne φ

k,j

(x) = 2

j/2

φ(2

x − k) (3.5.5)

then for each ﬁxed j, the system {φ

k,j

, k ∈ Z} is an orthonormal basis for V

Since V

⊂ V

, we can express φ in terms of the basis functions of V

φ(x) =

√

2φ(2x − k) (3.5.6)

Functions satisfying (3.5.6) are called scaling or reﬁnable functions and the sequence {a

}

is called the reﬁnement mask.

Let W

be the orthogonal complement of V

in V

, i.e. V

= V

⊕W

, V

⊥ W

. Deﬁne

a new function ψ by

ψ(x) =

√

2φ(2x − k), (3.5.7)

3.5. MULTISCALE REPRESENTATION 131

where

= (−1)

−k+1

, k ∈ Z (3.5.8)

The sequence {b

} is called the wavelet mask. It can be shown that the system {ψ(· −

k), k ∈ Z} forms an orthonormal basis of W

by using the fact that the system {φ(· −

k), k ∈ Z} forms an orthonormal basis of V

. The function ψ is called the wavelet function.

Now let W

be the j-th dilation of W

: f(x) ∈ W

if and only if f(2

x) ∈ W

. Then

by the deﬁnition of W

and MRA, W

is also the orthogonal complement of V

in V

j+1

i.e.

j+1

= V

⊕ W

, V

⊥ W

. (3.5.9)

Iterating this decomposition inﬁnitely many times and letting j → ∞, we obtain:

(R) =

⊕

j∈Z

= ⊕

j∈Z

. (3.5.10)

This states that L

(R) can be orthogonally decomposed into the sum of the spaces {W

Furthermore, if we deﬁne ψ

k,j

(x) = 2

j/2

ψ(2

x − k), (3.5.11)

then for each ﬁxed j, the system {ψ

k,j

, k ∈ Z} forms an orthonormal basis of W

and

the whole system {ψ

k,j

, j, k ∈ Z} forms an orthonormal basis of L

(R). It is clear from

the above discussion that the key point for constructing an orthonormal wavelet basis is

to construct the reﬁnable function.

Examples

The ﬁrst example is the Haar wavelet, obtained with the scaling function:

φ(x) =







1, 0 ≤ x < 1,

0, otherwise.

(3.5.12)

The function φ satisﬁes the following reﬁnement relation

φ(x) = φ(2x) + φ(2x − 1) =

√

(

√

2φ(2x) +

√

2φ(2x − 1)) (3.5.13)

with the reﬁnement mask

= a

√

, (3.5.14)

132 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

and a

= 0, k 6= 0, 1. The Haar wavelet function is given by:

ψ(x) =











1, 0 ≤ x < 1/2,

−1, 1/2 ≤ x < 1,

0, otherwise.

(3.5.15)

with the wavelet mask

√

, b

= −

√

, b

= 0, k 6= 0, 1. (3.5.16)

It is clear that

ψ(x) = φ(2x) − φ(2x − 1) (3.5.17)

The Haar wavelet is very localized, since it has the smallest support among all orthogo-

nal wavelets. However, it is not very smooth, which means that it decays slowly in Fourier

domain, and it has rather poor approximation properties. One can construct compactly

supported wavelets with better regularity and approximation properties, see the classic

text [16]. One way of systematically constructin g such compactly support ed wavelets

with better regularity and approximation property has been develop ed by Daubechies.

In her construction, the scaling functions are deﬁned by directly by their reﬁnement

masks, instead of giving an explicit analytical form.

Here, we give one example of 4-tap Daubechies’ wavelet and interested reader should

ﬁnd more in [16]. The reﬁnement mask of this example is deﬁned as:

1 +

√

, a

3 +

√

, a

3 −

√

, a

1 −

√

, a

= 0, k 6= 0, 1, 2, 3.

(3.5.18)

The corresponding wavelet mask is

−2

1 −

√

, b

−1

= −

3 −

√

, b

3 +

√

, b

= −

1 +

√

, b

= 0, k 6= 0, 1, 2, 3.

(3.5.19)

See Figure 3.5.2.

Given a function f ∈ L

(R), it can be approximated by its orthogonal projections

into V

for diﬀerent j’s:

k∈Z

hf, φ

k,j

iφ

k,j

. (3.5.20)

3.5. MULTISCALE REPRESENTATION 133

0 0.5 1 1.5 2 2.5 3

−1.5

−1

−0.5

0.5

1.5

scaling function

wavelet function

Figure 3.10: The scaling and wavelet functions of an example of Daubechies wavelets.

The accuracy of this approximation depends on the choice of j, which in practice is

usually determined by the data we have. For a given value of j, the accuracy then

depends on the smoothness of f and approximation properties of φ, especially the order

of the Strang-Fix condition that φ satisﬁes [36]. Recall that a function φ satisﬁes the

Strang-Fix (SF) condition of order m if

φ(0) 6= 0,

(j)

(2πk) = 0, j = 0, 1, 2, ..., m − 1, k ∈ Z\{0}, (3.5.21)

where

φ is the Fourier transform of φ. Assume that the scaling function satisﬁes the

Strang-Fix conditin of order m, then the spaces {V

} provides an order m approximation,

i.e. if f ∈ W

(R), then

kf − f

k = O(2

−jm

). (3.5.22)

Here the Sobolev spaces W

(R), m ∈ Z

are deﬁned by

(R) := {f ∈ L

(R) : kf k

(R)

√

2πk(1 + | · |)

fk < ∞}. (3.5.23)

The details about the approximation order can be found in [18].

134 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

The piecewise constant reﬁnable fun ction φ that leads to the Haar wavelet has ap-

proximation order 1. The scaling function of the 4-tap wavelet has approximation order

2. Scaling functions with higher approximation orders can be found in [16].

The decomposition and reconstruction algorithms

Given a function v in V

where V

represents the highest resolution we have, we would

like to express v as:

v = v

J−1

k=0

(3.5.24)

where v

∈ V

, w

∈ W

, j = 0, ··· , J − 1. Mallat developed a very eﬃcient hierarchical

algorithm for performing this decomposition [30]. The spirit of Mallat’s algorithm and

the hierarchical algorithm of Yserentant discussed earlier [42]. To see how this is done,

let us consider a simpler problem: Assume that v

∈ V

. We can write v

= v

j−1

+ w

j−1

where v

j−1

∈ V

j−1

, w

j−1

∈ W

j−1

, and v

k,j

, v

j−1

k,j−1

, w

j−1

k,j−1

. Note th at from (3.5.6) and (3.5.7), we have

k,j−1

m−2k

m,j

(3.5.25)

k,j−1

m−2k

m,j

(3.5.26)

It is easy to see then

k,j−1

= hv

, φ

k,j−1

i (3.5.27)

= hv

m−2k

m,j

m−2k

, φ

m,j

m−2k

m,j

Similarly,

k,j−1

m−2k

m,j

(3.5.28)

Knowing {c

m,j

}, {c

m,j−1

, d

m,j−1

} can be computed very simply from the formulas above.

This procedure can then be repeated.

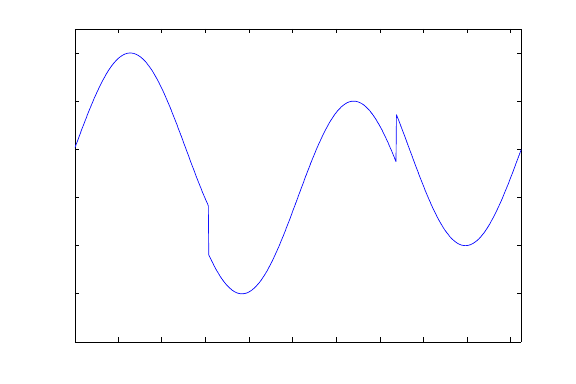
3.5. MULTISCALE REPRESENTATION 135

100 200 300 400 500 600 700 800 900 1000

−8

−6

−4

−2

c10

Figure 3.11: An example of a piecewise smooth function.

The decomposition algorithm described above can also b e used in the reverse direction

to reconstruct the ﬁne scale coeﬃcients in terms of the coeﬃcients at the coarser scale,

since we have

k,j

= hv

, φ

k,j

i (3.5.29)

m,j−1

hφ

m,j−1

, φ

k,j

i +

m,j−1

hψ

m,j−1

, φ

k,j

m−2k

m,j−1

m−2k

m,j−1

This gives a perfect reconstruction, in the sense decomposition followed by reconstruc-

tion leads to the identity transform. It is important to note that while scaling and

wavelet functions are used in analysis, only reﬁnement and wavelet masks are used in

decomposition and reconstruction algorithms.

What makes wavelets useful is that for many class of signals (or functions), their

wavelet coeﬃcients are approximately sparse, i.e. most wavelet coeﬃcients are very

small. In addition, the set of sizable ones is localized in the wavelet transform space.

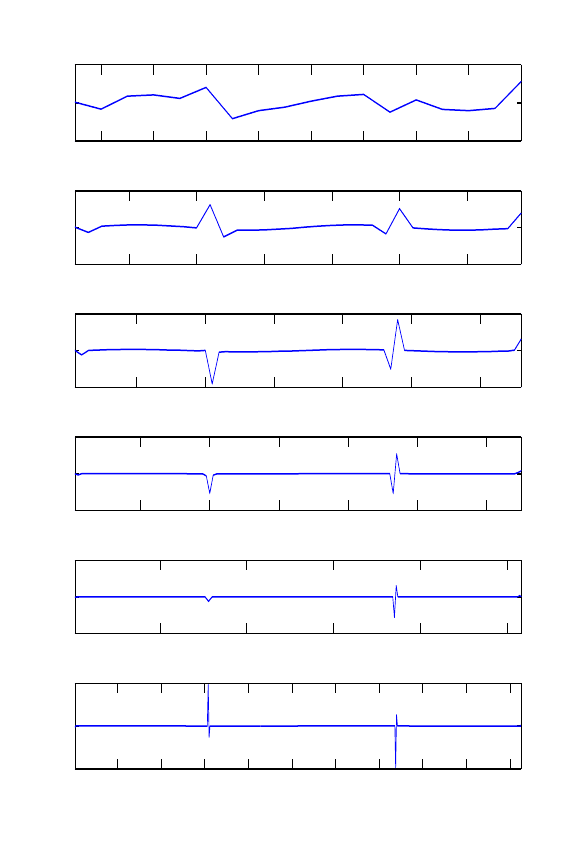
This is illustrated by the sequences of ﬁgures 3.5.2 to 3.5.2. 3.5.2 shows a piecewise

smooth function. 3.5.2 is the plot of the wavelet coeﬃcients at various levels. As shown

clearly in 3.5.2, the wavelet coeﬃcients are sparse.

136 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

2 4 6 8 10 12 14 16 18

−10

5 10 15 20 25 30

−5

10 20 30 40 50 60

−2

20 40 60 80 100 120

−2

50 100 150 200 250

−2

50 100 150 200 250 300 350 400 450 500

−1

Figure 3.12: The wavelet coeﬃcients at various levels for the function shown in the above

ﬁgure.