Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

3.1. MULTIGRID METHOD 97

such an error, one has to run the propagator, i.e. the iteration, at least O(1/h) times.

Of course, this argument would not work if the iterative procedure itself is global, which

is the case when global bases are used to represent the numerical solutions. Indeed, as

we discuss later in this chapter, it is possible to construct hierarchical bases for ﬁnite

element methods for which the condition number of A

is drastically reduced [42].

An important observation is that the slow convergence is caused mostly by the error

in the large scale components of the solution. Such large scale components can also be

accurately represented on coarser grids. Since it is less costly to eliminate the errors on

coarser grids, we should be able to construct much more eﬃcient iterative algorithms

by correcting the large scale components of the error on coarser grids. This is the main

intuition behind the multigrid method.

In order to turn this intuition into real algorithms, we have to know how to move the

numerical solutions across diﬀerent grids and how to set up the iterations on diﬀerent

grids. This is indeed the central issue of the multigrid method. Our presentation here

is very much inﬂuenced by the tutorial of Briggs et al. [13], which gives a very clear

introduction to this topic.

To illustrate the details of the algorithm, it is useful to consider the one-dimensional

case of (3.1.1). When Ω = [0, 1], (3.1.1) becomes

−

= f(x), x ∈ [0, 1] (3.1.4)

u(0) = u(1) = 0.

We consider a ﬁnite diﬀerence discretization on a grid with grid points x

= jh, j =

1, ··· , n − 1, and h = 1/n. Using a standard second order ﬁnite diﬀerence formula, we

obtain from (3.1.4)

−

j+1

− 2u

+ u

j−1

= f(x

), j = 1, ··· , n − 1

This can be written as

= f

, (3.1.5)

98 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

where







2 −1

−1 2 −1

2 −1

−1 2







is a (n−1)×(n−1) tri-diagonal matrix, u

= (u

, ··· , u

n−1

)

and f

= (f(x

), ··· , f(x

n−1

))

What makes this example particularly useful is that the eigenvalues and eigenvectors

of A

can be computed explicitly using discrete Fourier analysis. Here are the results:

1. The eigenvalues are

sin

(kπh/2), k = 1, ··· , n − 1. (3.1.6)

2. The eigenvect or w

corresponding to the eigenvalue λ

is given by:

(j) = sin(πkx

) = sin(πkj/n) (3.1.7)

The condition number is:

κ(A

) = max|λ

|/ min|λ

| =

sin

π(1−h)

sin

πh

= O(h

−2

) (3.1.8)

We now look at what happens when iterative methods are used to solve the linear

system (3.1.5). The simplest iterative algorithms can be written in the form:

n+1

= Bu

+ g (3.1.9)

where B is the iteration matrix. Let u

∗

be the exact solution of (3.1.5), and deﬁne the

error vector: e

= u

− u

∗

. If we express e

as a linear combination of the eigenvectors

of B, {v

, (3.1.10)

then

(µ

)

(3.1.11)

3.1. MULTIGRID METHOD 99

where µ

is the eigenvalue of B corresponding to the eigenvector v

. Hence

∼ (ρ(B))

(3.1.12)

where ρ(B) = max{|µ

|} is the spectral radius of B. The convergence rate is determined

by the spectrum of B.

Let D be the diagonal part of A

and L be the lower sub-diagonal part of −A

. Then

the symmetric matrix A

can be rewritten as A

= D − L − L

. Some of the simplest

iterative algorithms are:

1. Jacobi iteration:

n+1

= D

−1

(L + L

+ D

−1

. (3.1.13)

The Jacobi iteration matrix is given by:

= D

−1

(L + L

). (3.1.14)

Its eigenvectors are t he same as those of A

. Its eigenvalues are µ

= 1 −

2 sin

(πkh/2), k = 1, ··· , n − 1.

2. Gauss-Seidel iteration:

n+1

= (D −L)

−1

+ (D −L)

−1

. (3.1.15)

Thus, the Gauss-Seidel iteration matrix is

= (D −L)

−1

. (3.1.16)

3. Relaxation methods: Starting with

n+1

= Bu

+ g, (3.1.17)

we can construct the relaxed iteration scheme:

n+1

= (1 − ω)u

+ ω(Bu

+ g) (3.1.18)

The relaxed iteration matrix is given by:

= (1 − ω)I + ωB. (3.1.19)

One can choose the optimal value of ω in order to minimize the spectral r adius

of B

. The best known such relaxation method is the successive overrelaxation

method studied by David Young [41].

100 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

For the simple one-dimensional example discussed earlier, the spectral radius of B

ρ(B

) = µ

= 1 − 2 sin

(πh/2) ∼ 1 − π

/2 (3.1.20)

Hence

log ρ(B

) ∼ π

/2 (3.1.21)

To reduce the size of the error e

to a prescribed tolerance ε, the number of iterations

needed is roughly:

N ∼ log ε/ log ρ(B

) ∼ O(h

−2

) (3.1.22)

For the Gauss-Seidel iteration (see [13]),

ρ(B

) = cos

(πh) ∼ 1 − π

(3.1.23)

log ρ(B

) ∼ π

(3.1.24)

Compared with the Jacobi iteration, we have

log ρ(B

) ∼ 2 log ρ(B

) (3.1.25)

Therefore, Gauss-Seidel iteration is about twice as fast as the Jacobi iteration.

For the relaxed Jacobi iteration, the eigenvalues are µ

) = 1−2ω sin

(πkh/2) (see

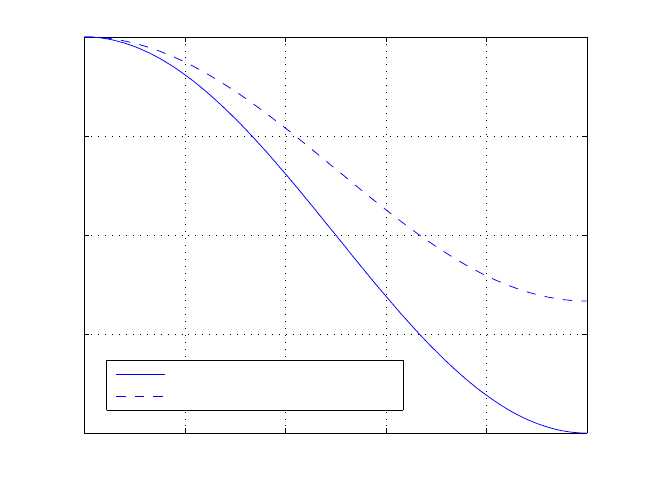
Fig. 3.1). Take ω = 2/3, then µ

) < 1/2 for k > n/2, i.e., the damping factor for

the high frequencies is less than 1/2 for the relaxed iteration method with ω = 2/3. This

is better than the Jacobi iteration. But for the low frequency components, the damping

factor is still of the order 1 −O(h

), which is comparable to that of the Jacobi iteration.

Note that the diﬃcult components are the low frequency components. Indeed for this

reason, the iteration procedure is also called smoothing: Th e numerical solution becomes

smoother after a few iteration steps since the high frequency components are eﬀectively

damped out. The low frequency components can be accurately represented on coarser

grids, on which the iterations converge faster. This is the key observation behind the

multigrid method. To turn this observation into an algorithm, we need to know the

following:

1. How do we transfer functions between diﬀerent grids?

2. What are the iterative procedures on each diﬀerent grid?

3.1. MULTIGRID METHOD 101

0 20 40 60 80 100

−1

−0.5

0.5

eigenvlaues (n=100)

Jacobi Iteration matrix

Relaxed Iteration matrix (ω=2/3)

Figure 3.1: The eigenvalues of Jacobi matrix and relaxed Jacobi matrix with ω = 2/3

(courtesy of Xiang Zhou).

102 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

To see how things work, let u s ﬁrst consider the two-grid algorithm, on the grids Ω

and Ω

that correspond to grid sizes h and 2h, respectively. The iteration scheme on

each grid can either be the relaxation method, or the Gauss-S eidel method. To transfer

between functions deﬁned on Ω

and Ω

, we will make use of the so-called restriction (or

projection) operators, which map functions deﬁned on ﬁne grids to functions on coarser

grids,

: Ω

→ Ω

and the interpolation (or the prolongation) operators, which map functions deﬁned on

coarse grids to functions on ﬁner grids,

: Ω

→ Ω

With these operators, the two-grid algorithm can be expressed in the following form:

1. Run a few smoothing steps on Ω

using some simple iteration algorithms such as

the Gauss-Seidel or the relaxation method.

2. Calculate the residual: r

= A

− f

3. Project to coarse grid: r

= I

4. Solve on coarse grid: A

= r

5. Interpolate to ﬁne grid: u

← u

− I

It remains to specify the intergrid operators I

, I

and the operator A

on the

coarse grid. In principle, A

should be the eﬀective operator on Ω

. In some situations,

e.g. problems of the type treated in Chapter 8 or molecular dynamics models, it can be

quite non-trivial to ﬁnd a good A

. However, for the problem considered here, one may

simply choose A

to be the corresponding matrix obtained by discretizing (3.1.1) on the

coarse grid with mesh size 2h. One may also choose:

= I

To deﬁne I

, let v

be any function deﬁned on the grid Ω

. We may simply deﬁne

as a function on Ω

obtained by evaluating v

on Ω

(j) := I

) (j) = v

(2j), j = 1, 2, ··· , n/2 − 1.

3.1. MULTIGRID METHOD 103

In matrix form, we have







(1)

(2)

(

− 1)

(

)













0 1 0 0 0 ··· 0 0

0 0 0 1 0 ··· 0 0

0 0 0 0 0 ··· 0 1













(1)

(2)

(n − 1)

(n)







We may also deﬁne I

through averaging over neighboring grid points. For example,

we can use averaging over the nearest neighbors with weights (

(j) := I

) (j) =

(2j − 1) +

(2j) +

(2j + 1).

In matrix form, this is







(1)

(2)

(

− 1)

(

)













1/4 1/2 1/4 0 0 ··· 0

0 0 1/4 1/2 1/4 0 ··· 0

0 0 0 0 0 ··· 0 1













(1)

(2)

(n − 1)

(n)







(3.1.26)

For I

, we may deﬁne it to be (a constant multiple of) the adjoint operator (or

transpose) of I

. For example, if I

is given by (3.1.26), we may deﬁne I







(1)

(2)

(n − 1)

(n)













0 0 ··· 0

1 0 0 ··· 0

0 ··· 0

0 1 0 ··· 0

··· 0

0 0 0 ··· 1













(1)

(2)

(

− 1)

(

)







. (3.1.27)

This simply means that on coarse grid points, v

= I

takes the same values as v

On the r emaining grid points, the value of v

is obtained th rough averaging the values

on the neighboring coarse grid points. In this case, I

= 2(I

)

Instead of averaging, one can also use linear interpolation to obtain the values of v

on the remaining grid points.

104 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

To understand the convergence properties of such a procedure, note that we can write

the iteration matrix as

= (I − I

−1

)(B

J,ω

)

where B

J,ω

= (1 − ω)I + ωB

, m is the number of smoothing steps on Ω

. Here we

have assumed that the relaxed Jacobi method is used as the smoothing operator. Even

though the {w

}’s deﬁned in (3.1.7) are no longer the eigenvectors of B

, the subspace

spanned by the pair (w

, w

′

), k

′

= n−k is still an invariant subspace of the matrix B

In fact, it is easy to see that if I

and I

are deﬁned as in (3.1.26) and (3.1.27), then

we have



1 − 2ω sin

kπh



sin

kπh



+ w

′



(3.1.28)

′



1 − 2ω sin

′

πh



cos

kπh



+ w

′



(3.1.29)

k = 1, ··· , n/2. Take ω = 2/3. For the high frequency components corresponding to k

′

the damping factor is less than 1/2 as indicated above in Fig. 3.1. For the low frequency

components corresponding to k, the factor sin

(kπh/2), which is less than 1/2, helps to

reduce the damping factor to less than 1/2. Therefore, as long as m ≥ 1, the damping

factor is uniformly less than 1/2 for all frequencies.

This two-grid algorithm can be easily generalized so that more grids, Ω

, Ω

, ···, are

used. Instead of solving the equation A

= r

exactly, we apply the same two-grid

algorithm again on this equation, and proceed recursively. In this case, it is important to

specify an overall strategy for moving from grid to grid. We may either follow a V -cycle

or a W -cycle. In a V -cycle, one starts from the ﬁne grid Ω

and then move to coarser

and coarser grids until the coarsest grid is reached, and then reverse the procedure. In a

W -cycle, one may reverse the direction before the ﬁnest or the coarsest grid is reached

[13].

In this example, the mechanism responsible for the eﬀectiveness of the multigrid

method lies in the smoothing eﬀect of the iterative algorithms on each grid. One should

not get the impression that this is the only way that the multigrid method can be

eﬀective. Multigrid method has been extended to many other situations such as steady

state calculations of transonic ﬂows [14], and Monte Carlo sampling methods [24] (see

[12]). In these cases, the explanation given above is no longer suﬃcient. At the present

3.1. MULTIGRID METHOD 105

0 20 40 60 80 100

−1

−0.5

0.5

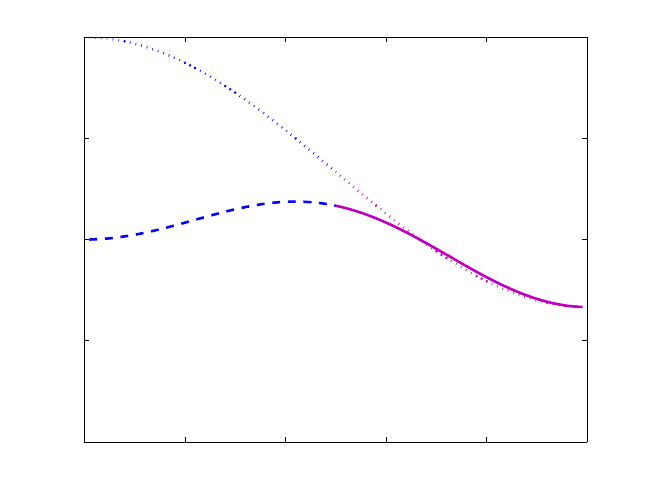
Figure 3.2: The damping factors in (3.1.28) and (3.1.29). Dashed-line: low frequency

components k = 1, ··· , n/2; solid line: high frequency components k

′

= n−k. The result

from the relaxed Jacobi iteration method (the dotted curve, the same as in Fig. 3.1) is

also shown for comparison (courtesy of Xiang Zhou).

106 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

time, a uniﬁed general understanding of the mechanisms behind the eﬀectiveness of the

multigrid method is still lacking.

3.2 Fast summation methods

We now turn to fast summation methods. The general problem treated by such fast

summation methods can be formulated as follows: Given a kernel K(x, y) and a set of

sources located at {x

} with weights {w

}, as well as a set of target locations {y

}, we

want to compute

j=1

K(x

, y

) (3.2.1)

for k = 1, ··· , M. Let us assume that M and N are comp arable in size. Some examples

of the kernels include:

1. The gravitational and Coulombic potential, K(x, y) =

|x−y|

2. The gravitational force, K(x, y) =

x−y

|x−y|

3. The heat kernel, K(x, y) = e

−

|x−y|

We will focus on the analysis-based fast algorithms, of which the fast multi-pole method

(FMM) is the primary example. These algorithms are based on the analytical properties

of the kernels involved in the problem. They should be contrasted to the other class of

fast algorithms, such as the fast Fourier transform (FFT), which is based on the algebraic

properties of the summands.

If we calculate (3.2.1) by direct summation, the cost is O(N

). The tree code, which

was a prelude to FMM, brings the cost down to O(N log N). FMM brings the cost

down further to O(N) for arbitrary precision. However, it should be pointed out that

the importance of FMM is not just to remove the logarithmic factor in the cost, it

establishes a new framework for designing hierarchical algorithms based on analytical

approximations, making it possible to develop fast summation algorithms beyond the

use of multi-pole expansions.