Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

3.2. FAST SUMMATION METHODS 107

3.2.1 Low rank kernels

Assume that the kernel is in a tensor product form, say K(x, y) = K

(x)K

(y), then

to evaluate

j=1

)

for a set of sources {x

} and targets {y

}, we may simply compute

A =

j=1

)

and then use

= AK

)

This requires only O(M + N) operations.

Tensor product kernels are rank-1 kernels. Kernels of practical interest are rarely

in the tensor product form. Fortunately, some important ones can be very accurately

approximated by the sum of a small number of kernels in tensor product form:

K(x, y) ≈

n=1

n,1

(x)K

n,2

(y) (3.2.2)

In this case, we can use

≈

j=1

n=1

n,1

n,2

)

n=1

n,1

)

where M

j=1

n,2

) are called the moments. The cost for computing the

moments is O(N p). The additional cost for computing all the u

’s is O(Mp). Thus the

total computational cost is O(Mp + Np).

(3.2.2) means that the kernel K is very well approximated by a kernel whose rank is

no greater than p. The Gauss transform is one such example.

Consider the two-dimensional Gauss transform [26]

u(y) =

j=1

−|y−x

/4T

. (3.2.3)

108 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

A key observation is the following Taylor series expansion for one-dimensional heat ker-

nels:

−(x−x

)

∞

n=0

(x)

where h

(x) is the n-th order Hermite function,

(x) = (−1)



−x



In two dimension, we have, for any c ∈ R

−|x−x

/4T

∞

(x − c)Ψ

− c) (3.2.4)

where (x = (x, y))

(x) = h



√





√



(x) =



√





√



More importantly, if ||x

− c|| ≤

√

T , then we have [26]

−|x−x

/4T

−

(x − c)Ψ

− c)| ≤







(3.2.5)

The right hand side decays very fast as p increases. This means that the heat kernel is

very well approximated by low rank kernels.

Assume ﬁrst that all the sources {x

} are located in a square centered at c with side

√

T . Then

j=1

−|y

−x

/4T

can be approximated by

≈

j=1

− c)Ψ

− c).

One can then use the ideas discussed earlier.

In the general case, let us cover all the sources and targets by a bounding box. If the

box has side length larger than

√

T , we divide the bounding box into smaller boxes of

3.2. FAST SUMMATION METHODS 109

size

√

T . Due to the very fast exponential decay of the heat kernel, to calculate u

for

each target y

, we only need to sum over the contribution from the sources which lie in

the (2n + 1)

neighboring boxes, i.e.,

−|y

−x

|/4T

∈N

−|y

−x

|/4T

+ O(e

−n

), (3.2.6)

Here n is a parameter that can be used to control the accuracy of the algorithm, N

the collection of the boxes within distance n

√

T from the box where the target y

lies

in (|N

| = (2n + 1)

in two dimension). Using (3.2.5), we can compute the moments for

each box B,

∈B

− c

where c

is the center of the b ox B. The amount of work required for computing the

moments for all the small boxes is Np

. Since the moments are independent of the

targets, they can be precomputed. Now for each target y

, (3.2.6) can be calculated

approximately by:

≈

B∈N

− c

The computational cost for evaluating this sum is (2n + 1)

M. Thus the total cost is

proportional to M + N.

3.2.2 Hierarchical algorithms

We will restrict ourselves to two dimensions for simplicity, with the kernel given by

K(x, x

) = −log(kx − x

k) (3.2.7)

In this case, it is much more convenient to use complex variables. Identifying x = (x, y)

with the complex number z = x + yi, and x

= (x

, y

) with the complex number

= x

+ y

i, we can then write (3.2.7) as

K(x, x

) = Re(−log(z − z

)) (3.2.8)

We will view the analytic function log(z −z

) as the potential due to a unit point charge

located at z

110 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

Consider now a point charge of strength q, located at z

. It is well-known that for

any z with |z| > |z

log(z − z

) = log(z) −

∞

k=1





(3.2.9)

This is the Taylor expansion in z

or Laurent expansion in z. If there are m charges

of strengths {q

, i = 1, ··· , m} located at the points {z

, i = 1, ··· , m} respectively,

such that max

| < r, then according to (3.2.9), if |z| > r, the potential φ(z) =

log(z − z

) induced by the charges is given by,

φ(z) = Q log(z) +

∞

k=1

(3.2.10)

where

Q =

, a

= −

This is called the multi-pole expansion of φ. The coeﬃcients {a

} are generally referred

to as the moments. If we truncate this series after p terms, the error incurred is bounded

by [7, 25]:

|φ(z) − Q log(z) −

k=1

| ≤



p + 1



c − 1





(3.2.11)

where c = |z/r| and A =

|. Note that the error bound depends on the target z

through the parameter c. If we choose c ≥ 2, then the error is bounded by A/2

. If we

want the error to be smaller than δ, we need to use p = −log

δ terms in the expansion

(3.2.10).

This observation together with a hierarchical strategy is the basis for the “tree code”

developed by Appel [2], Barnes and Hut [6].

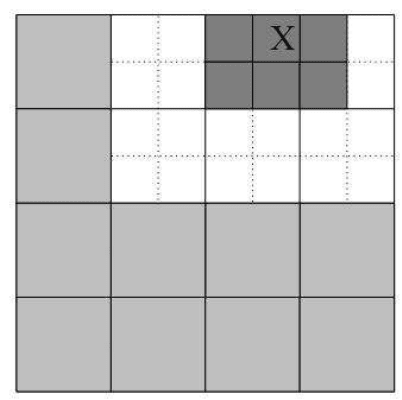
Suppose that the particles are distributed in a square and this square is divided into

× 2

boxes, see Figure 3.3 for l = 2. Two boxes are nearest neighbors if they share a

boundary point. Two boxes are said to be well separated if they are not nearest neighbors.

For example, the grey boxes in Figure 3.3 are nearest neighbors of the box X and the white

boxes are well separated from the box X. We want to evaluate φ(z) =

i=1

log(z−z

) ≈

at a location z which lies in, say the box X. Denote the collection of well separated boxes

from box X by W(z). For the z

’s that are in boxes belonging to W(z), the multi-pole

3.2. FAST SUMMATION METHODS 111

expansion (3.2.10) gives

∈W(z)

log(z − z

)

B∈W(z)

∈B

log(z − z

0,B

) −

k=1

− z

0,B

)

k(z − z

0,B

)

(3.2.12)

where z

0,B

is the center of the box B. Let

k,B

= −

∈B

− z

0,B

)

, q

{i:z

∈B}

Then the use of multi-pole expansion for contributions from well separated boxes W(z)

leads to the following,

φ(z) =

i=1

log(z − z

) (3.2.13)

≈

B∈N(z)

∈B

log(z − z

)

B∈W(z)

log(z − z

0,B

) −

k=1

k,B

(z − z

0,B

)

where N(z) is the collection of the nearest neighbor boxes of the box containing z. The

error made in these approximations can be estimated explicitly using (3.2.11).

Next, we apply the same idea to calculate the interaction between charges in the box

X and its nearest neighbors,

B∈N(z)

∈B

log(z − z

)

by subdividing each box into four smaller boxes. To do this systematically, we build a

tree of a hierarchy of boxes. This can be done inductively. At level 0, we have the entire

computational domain. The level l + 1 boxes are obtained recursively from the level l

boxes by subdividing each box into four equal parts. This yields a natural (quad-) tree

structure, where for each box, the four boxes obtained by subdividing it are considered

its children. If we assume that the particles are fairly homogeneously distribu ted, then

we need roughly log

N levels to obtain N boxes at the ﬁnest scale. On average, each

smallest b ox contains roughly one charge. We will denote by L the number of levels, i.e.,

l = L is the ﬁnest level.

112 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

With each box X we associate an interaction list deﬁned in the following way: De-

note the parent of X as

X. Consider the children of the nearest neighbors of

X. The

interaction list of X is deﬁned as the subset of th is collection of boxes which are not the

nearest neighbors of X. Obviously boxes in the interaction list of X are at the same level

as X. For example, in Figure 3.4, the white boxes are in the interaction list of the box

X. The multi-pole expansion is going to be used to calculate the potential inside the box

X due to the charges in the boxes belonging to the interaction list of X.

Given a target z, let B

(z) be the level l box that contains z. Let N

(z) be the

collection of the nearest neighbor boxes of B

(z) and let L

(z) be the interaction list of

(z). It is easy to see that

B∈N

(z)

∈B

log(z − z

) =

B∈L

l+1

(z)

∈B

log(z − z

) +

B∈N

l+1

(z)

∈B

log(z − z

The calculation of the ﬁrst term in the right hand side can be done using the multi-pole

expansion. For the second term, we can use (3.2.2) recursively with l replaced by l + 1.

These recursive steps can be continued u ntil the ﬁnest level is reached. At that p oint,

one can use direct summation to compute the potential due to the charges in the nearest

neighbor boxes. In other words, we have, for all z

log(z − z

) =

l<L

B∈L

(z)

∈B

log(z − z

) +

B∈N

(z)

∈B

log(z − z

Note that the coeﬃcients in the multi-pole expansions are independent of the targets.

They can be precomputed. The total cost for pre-computing the moments for the boxes

in all O(log N) levels is approximately Np log N. For each target in a given box, 27p

operations are required to compute the interaction with the boxes in the interaction list

at each reﬁnement level. A total of 27p log N operations are needed for each target. At

the ﬁnest level, there are on average one particle in each nearest neighbor box, therefore

8 operations are required for each target. Hence, the total cost is approximately

28Np log N + 8N.

3.2.3 The fast multi-pole method

In order to obtain a linear scaling algorithm, let us examine the origin of the O(N log N)

cost. First, the computation of the moments in order to build the multi-pole expansion

3.2. FAST SUMMATION METHODS 113

Figure 3.3: The ﬁrst step of the tree code. Interaction between particles in box X and

the while boxes can be computed via multi-p ole expansions. Interaction with nearest

neighbor boxes (grey) are not computed.

for all boxes at all levels requires pN log N operations. This can be avoided if we know

how to eﬃciently build the multi-pole expansion for a box from the multi-pole expansion

of its four children. The main issue is that the multi-pole expansions for the four chil-

dren boxes are centered at the center of each of the children box, whereas the multi-pole

expansion for the parent box should be centered at the center of the parent box. The

following simple lemma tells us how to translate a multi-pole expansion with respect to

one center to a multi-pole expansion with respect to a diﬀerent center.

Lemma 3 (Translation of multi-pole expansion). Suppose that

i=1

log(z − z

) = a

log(z − z

) +

∞

k=1

(z − z

)

(3.2.14)

is a multi-pole expansion of the potential due to a set of m charges of strengths {q

, i =

1, ··· , m} such that max

− z

| < R. If z satisﬁes |z| < R + |z

|, p > 1, then

i=1

log(z − z

) − a

log(z) −

l=1

| ≤



1 − |c|



|c|

p+1

(3.2.15)

114 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

Figure 3.4: The second step of the tree code. After reﬁnement, l = 3. Interaction

between particles in box X (note at current level box X is one of the children of the box

“X” in Fig. 3.3) and the light grey boxes has been calculated. The white boxes are well

separated with box X at level l = 3. Therefore these interactions can been calculated

using multi-pole expansion again. Bu t the nearest neighbor interactions (dark grey) are

not computed at this level.

3.2. FAST SUMMATION METHODS 115

where c =

|+R

, A =

i=1

| and

= −

k=1

l−k



l − 1

k − 1



. (3.2.16)

This lemma tells us how to convert a multi-pole expansion centered at z

to a multi-

pole expansion centered at 0.

Using this lemma, we can develop an upward pass procedure to build the multi-pole

expansions for all the boxes, starting from the multi-pole expansion for the boxes at the

ﬁnest level. This reduces the cost of forming multi-pole expansions from O(N log N) to

O(pN + 4p

log N).

The second source of the O(N log N) cost in the tree code comes from the fact that

the value of the potential is evaluated separately for each target, and the calculation for

each target costs O(log N) since the interaction list at all levels has to be visited and there

are O(log N) interaction lists for each target. The fast multi-pole method overcomes this

problem by introducing local expansions.

For any given box X at some reﬁnement level, we will set up an expansion for the

potential at any position in box X due to all the sources located outside of the nearest

neighbors of X. This expansion is called the local expansion.

Lemma 4. Suppose that

i=1

log(z − z

) = a

log(z − z

) +

∞

k=1

(z − z

)

is a multiple expansion of the potential due to a set of m charges of strengths {q

, i =

1, ··· , m} such that max

−z

| < R and |z

| > (c+1)R. Then, if z is such that |z| < R

and if p > 1,

i=1

log(z − z

) −

l=0

| ≤

A(4e(p + c)(c + 1) + c

)

c(c − 1)





p+1

where b

= a

log(−z

) +

∞

k=1

(−1)

and

= −

∞

k=1



l + k − 1

k − 1



(−1)

116 CHAPTER 3. CLASSICAL MULTISCALE ALGORITHMS

This lemma allows us to convert multi-p ole expansions into local expansions. Note

that contrary to the multi-pole expansions which are centered at the centers of the boxes

where the sources lie in, the local expansions are centered at the centers of the boxes

where the targets lie in.

Once we have the local expansions for all the boxes, the ﬁnal step is to distribute

the contributions of the sources in each box to the targets in its interaction list. For

this purpose, we need t o translate a local expansion with respect to one center to a lo cal

expansion with respect to a diﬀerent center, i.e. we need to convert an expansion of the

form

k=0

(z −z

)

to a form

k=0

. This can be done using the standard Horner

algorithm.

We are ready to describe the main steps in FMM.

1. Initialization : Build log

(N/s) levels of boxes so that there are, on average, s

particles per box at the ﬁnest level.

2. Upward Pass: Beginning at the ﬁnest level, create the multi-pole expansions of the

potential for each box due to the sources in this box. The expansions for all boxes

at coarser levels are then formed by the merging procedure described in Lemma 3.

The cost is O(Np + p

N/s).

3. Downward Pass: Beginning at the coarsest level, convert the multi-pole expansion

of each box to a local expansion about the centers of the boxes in its interaction

list. These local expansions are shifted to their children’s level, using the Horner

algorithm described above. Therefore at each level, the local expansion for each

box receives contributions from two sources: The contribution inherited from the

parent box, and the contributions from sources in its interaction list.

At t he ﬁnest level, we have local expansions for each ﬁnest scale box, which ac-

count for contributions from charges that lie outside the nearest n eighors of each

box. These local expansions are then evaluated at each target. Contributions from

neighboring ﬁnest level boxes are computed directly.

The cost for pre-computing the local expansions is O(p

N/s). The cost for evaluating

the local expansions at the targets is O(pN/s). Thus the total cost in this step is

O(Np

/s). The cost for the direct summation over the nearest neighbors at the ﬁnest