Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach
Подождите немного. Документ загружается.


44 CHAPTER 2 An Integral Approach to Uniform Subdivision
same projection onto x have been summed.) Because cross-sectional area is scaled
by a factor of
1
4
when the cube H
3
is split, these cross-sectional areas satisfy the
recurrence
n
3
[x] ==
1
4
n
3
[2x] +
3
4
n
3
[2x − 1] +
3
4
n
3
[2x − 2] +
1
4
n
3
[2x − 3].
Again, this equation is exactly the refinement relation for a quadratic B-spline.
2.2.2 Box-spline Scaling Functions as Cross-sectional Volumes
The beauty of this geometric construction for B-spline basis functions is that it
immediately implies the existence of a refinement relation for the basis functions.
De Boor and H
¨
ollig [39] observed that this construction can be generalized to
produce smooth multivariate scaling functions that are also refineable. (Note that
integer translates of these scaling functions are not necessarily linearly independent,
and hence not necessarily basis functions.) The key idea is to define a set of direction
vectors
of the form {{a
i
, b
i
}∈Z
2
|i = 1, ..., m} and then consider the cross-sectional
volume of the form
vol
m−2
{t
1
, ..., t
m
}∈H
m
m
i =1
{a
i
, b
i
}t
i
== {x, y}
. (2.14)
If this function is normalized to have unit integral, the resulting function n
[x, y]
is the box-spline scaling function associated with the direction vectors . Note that
instead of computing the
(m − 1)-dimensional volume of the intersection of H
m
and
an
(m−1)-dimensional hyperplane this definition computes the (m −2)-dimensional
volume of the intersection of
H
m
and two (m − 1)-dimensional hyperplanes of the
form
m
i =1
a
i
t
i
== x and
m
i =1
b
i
t
i
== y. One way to visualize the relation between
the hypercube
H
m
and the direction vectors {a
i
, b
i
} is to orient H
m
with respect to
the
xy plane such that the origin of H
m
projects onto the origin of the xy plane
and the coordinate axes of
H
m
project onto the line segments defined by placing
the direction vectors
{a
i
, b
i
} at the origin. Based on this definition, the following
properties follow (almost) immediately:
■
n
[x, y] is a piecewise polynomial function of degree m−2 with C
α−2
continu-
ity, where
α is the size of the smallest subset A ⊂ such that the complement
of
A in does not span R
2
.
■
n
[x, y] is non-negative and is supported on the domain {
m
i =1
{a
i
, b
i
}t
i
|0 ≤
t
i
< 1}.
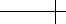
2.2 A Subdivision Scheme for Box Splines 45
■
n
[x, y] has unit integral by construction. As in the case of B-splines, this
property can be strengthened to
i, j
n
[x − i, y − j] == 1.
The only one of these properties that requires substantial analysis is the smooth-
ness bound of
C
α−2
. In the case of B-splines, the basis functions n
m
[x] always have
maximal smoothness (i.e.,
C
m−2
). However, box-spline scaling functions n
[x, y] do
not always achieve the maximum possible smoothness of
C
m−3
. If the direction
vectors in
are independent (i.e., no two vectors are constant multiples of each
other), all but one of the vectors must be removed from
for the space of the
remaining vectors to collapse to a line. In this case, the box-spline scaling function
has maximal smoothness
C
m−3
, in that α == m − 1. However, if one of the direction
vectors in
is repeated several times, removing all vectors except for this repeated
vector leads to
α<m −1. In this case, the box-spline scaling function does not have
maximal smoothness. See section 2.2.4 for examples of computing the smoothness
of various box splines.
Geometrically, the effect of repeated direction vectors on the resulting projec-
tion of
H
m
is to cause a higher-dimensional face of H
m
to project onto a line segment
in the
xy plane. As a result, the cross-sectional volume of the hypercube H
m
taken
across this edge no longer has the maximal smoothness of
C
m−3
. For a more detailed
analysis of this and other properties of box splines, we direct the interested reader
to [40].
2.2.3 Subdivision for Box Splines
Our next task is to derive a refinement relation (and the corresponding subdivision
mask) for the box-spline scaling functions
n
[x, y]. Geometrically, this refinement
relation is a consequence of splitting the hypercube
H
m
into 2
m
subcubes. To
compute the actual coefficients of this refinement relation, we instead reformu-
late box splines in terms of an inductive definition based on repeated integration
(as done for B-splines in equation 2.3). The subdivision mask for box splines then
follows from a variant of Theorem 2.1.
To simplify this recursive definition, we always choose the set
of direction
vectors to consist of the two standard unit vectors,
{1, 0} and {0, 1} in the base case. In
this case, the box-spline scaling function
n
[x, y] is simply the step function defined
over the unit square:
n
[x, y] =
1 if 0 ≤ x < 1 and 0 ≤ y < 1,
0 otherwise.
(2.15)

46 CHAPTER 2 An Integral Approach to Uniform Subdivision
Larger sets of direction vectors are formed by inductively adding new direction
vectors to this initial set. Given an existing set of direction vectors
∼
and associated
box-spline scaling function
n
[x, y], the box-spline scaling function associated with
the set
=
∼
∪{{a, b}} has the form
n
[x, y] =
1
0
n
[x − at, y − bt] dt.
A proof of the equivalence of this recursive definition of n
[x, y] to the definition of
equation 2.14 is almost identical to the proof of Theorem 2.2. The main difference
is that the
(m − 2)
-dimensional volume of equation 2.14 is reduced to the integral
of
(m − 3)-dimensional volumes in a manner similar to that of equation 2.12 for
B-splines.
Given this definition (in terms of repeated directional integration), we next
establish the link between repeated directional integration and subdivision. For the
base case of
={{1, 0}, {0, 1}}, the two-direction constant box splines of equa-
tion 2.15 satisfy the following refinement relation:
n
[x, y] == n
[2x, 2y] + n
[2x − 1, 2y] + n
[2x, 2y − 1] + n
[2x − 1, 2y − 1].
This relation simply states that a constant function defined over the unit square
can be expressed as the sum of four constant functions, each defined over one of
four subsquares that constitute the original square. The coefficients of this relation
define the subdivision mask for this scaling function,
s
[x, y] = (1 +x)(1 + y). Next,
based on the recursive definition of
n
[x, y], we recursively construct the subdivision
mask
s
[x, y] for box splines. This mask satisfies a refinement relation of the form
n
[x, y] ==
i
s
[[ i , j]]n
[2x − i, 2y − j].
Theorem 2.3, which follows, generalizes Theorem 2.1 and establishes the effect
of integration in the direction
{a, b} on the subdivision mask for a scaling function.
THEOREM
2.3
Let
∼
= ∪{{a, b}}.Ifs
[x, y] is the subdivision mask for n
[x, y], the sub-
division mask
s
[x, y] for n
[x, y] has the form
s
[x, y] =
1
2
(1 + x
a
y
b
)s
[x, y].
Proof The proof is entirely analogous to that of Theorem 2.1.

2.2 A Subdivision Scheme for Box Splines 47
Recursively applying Theorem 2.3 to a set of direction vectors , we note that the
subdivision mask
s
[x, y] has the explicit form
s
[x, y] = 4
{a,b}∈
1 + x
a
y
b
2
.
(2.16)
The factor of four here arises from rewriting the mask s
[x, y] for the base case
={{1, 0}, {0, 1}}
as 4
(1+x)
2
(1+y)
2
. If the vector
{a, b} appears multiple times in , the
corresponding factor
1+x
a
y
b
2
should appear to the appropriate power.
A box spline
p[x, y] is simply a linear combination of integer translates of the
box-spline scaling function
n
[x − i, y − j]; that is, a sum of the form
i, j
p
0
[[ i , j]]
n
[x−i, y−j], where p
0
[[ i , j]]is the entry of the vector p
0
attached to the point {i, j }in
the grid
Z
2
. As in the univariate case, we write this sum in vector form as N
[x, y]p
0
.
Subdividing the entries of basis vector
N
[x, y] using the subdivision mask s
allows
the function
p[x, y] to be expressed as a sum of the form N
[2
k
x, 2
k
y]p
k
.Ifp
k−1
[x, y]
and p
k
[x, y]
are the generating functions associated with successive coefficient vec-
tors
p
k−1
and p
k
, these generating functions are related via the expression
p
k
[x, y] = s
[x, y]p
k−1
[x
2
, y
2
]. (2.17)
Note that Theorem 2.3 makes clear the need to restrict the direction vector {a, b}
to the integer grid Z
2
. Allowing nonintegral values for a and b would give rise to
a refinement relation for
N
[x, y] that does not involve members of the vector
N
[2x, 2y] and would therefore make this type of subdivision process impossible.
For box splines, the subdivision relation of equation 2.17 gives rise to four types
of subdivision rules (as opposed to the two rules of equation 2.9 in the univariate
case). These four rules take convex combination of
p
k−1
using the weights of the
form
s
[[ 2 i , 2j]], s
[[ 2 i +1, 2j]], s
[[ 2 i , 2j + 1]], and s
[[ 2 i +1, 2j + 1]], where {i, j }∈Z
2
.
In the one-dimensional case, the
i th coefficient of p
k
was plotted over x ==
i
2
k
to form a discrete approximation to the B-spline p[x]. In the case of box splines, the
ijth coefficient of p
k
is plotted at {x, y} == {
i
2
k
,
j
2
k
}. As long as the set of direction
vectors
includes the initial directions {1, 0} and {0, 1}, the polyhedra formed by
the
p
k
converge to the box-spline function p[x, y]. For those readers interested in a
proof of this convergence result, we recommend Cohen et al. [25] and Dahmen
and Micchelli [33]. Chapter 3 also provides tools for addressing this question.
In the univariate case, Theorem 2.1 led to a repeated averaging algorithm for
B-spline subdivision. For box splines, Theorem 2.3 yields a similar repeated aver-
aging algorithm for box-spline subdivision. Given a set of coefficients
p
k−1
on the

48 CHAPTER 2 An Integral Approach to Uniform Subdivision
coarse grid
1
2
k−1
Z
2
, the algorithm computes a set of coefficients p
k
on the refined
grid
1
2
k
Z
2
as follows:
■
Construct the generating function p
k−1
[x, y] from p
k−1
. Upsample p
k−1
[x, y]
to yield p
k−1
[x
2
, y
2
]. Set p
k
[x, y] = 4p
k−1
[x
2
, y
2
].
■
For each direction vector {a, b}∈, update p
k
[x, y] via the recurrence
p
k
[x, y] =
(1+x
a
y
b
)
2
p
k
[x, y]. Each multiplication by
(1+x
a
y
b
)
2
corresponds to mid-
point averaging on
p
k
in the direction {a, b}.
■
Extract the coefficients p
k
of the generating function p
k
[x, y].
2.2.4 Examples
We conclude this section by considering three examples of well-known box splines.
Three-direction Linear Splines
In Chapter 1, we considered a subdivision scheme for piecewise linear hat functions.
These hat functions can be generalized to a triangular grid in two dimensions. If
each triangle in the grid is subdivided into four subtriangles, the hat functions can
be refined in a manner similar to that of the univariate case. For uniform triangular
grids, this subdivision process can be expressed in terms of three-direction box
splines. Let
consist of the set of three direction vectors {{1, 0}, {0, 1}, {1, 1}}.For
k == 0, the resulting grid consists of triangles bounded by lines of the form x == i ,
y == j , and x − y == h, where h, i, j ∈ Z. Applying equation 2.16, we obtain the
subdivision mask for this scheme:
s
[x, y] = 4
1 + x
1
y
0
2
1 + x
0
y
1
2
1 + x
1
y
1
2
=
(1 + x)(1 + y)(1 + xy)
2
.
The coefficients of this subdivision mask s
can be visualized as a two-dimensional
array of the form
s
[x, y] == (
1xx
2
)
⎛
⎜
⎜
⎝
1
2
1
2
0
1
2
1
1
2
0
1
2
1
2
⎞
⎟
⎟
⎠
⎛
⎜
⎝
1
y
y
2
⎞
⎟
⎠
.
Note that this 3 × 3 matrix is not the subdivision matrix S but a plot of a single
column of
S as a two-dimensional array. The four subdivision rules for this scheme
2.2 A Subdivision Scheme for Box Splines 49
0
0
1
1
3
2
0
.25
.5
.75
1
1
1
2
3
0
0
1
1
3
2
0
.25
.5
.75
1
1
1
2
3
0
0
1
1
3
2
0
.25
.5
.75
1
1
1
2
3
Figure 2.12 Three rounds of subdivision for the linear box-spline basis function.
correspond to taking convex combinations of the entries of the vector p
k−1
using
the weights
1
2
0
0
1
2
,(
1
2
1
2
),
1
2
1
2
,(1).
The basis function
n
[x, y]
associated with this scheme is piecewise linear and is
supported over the hexagon consisting of all points of the form
{1, 0}t
1
+{0, 1}t
2
+
{1, 1}t
3
, where 0 ≤ t
i
< 1. The basis function is C
0
(i.e., α == 2) because removing
any two vectors from
causes the remaining vector to fail to span the plane R
2
.
Figure 2.12 shows the results of three rounds of subdivision using this scheme,
applied to the initial generating function
p
0
[x, y] = 1. In each plot, the coefficients
of
p
k
are taken on the grid
1
2
k
Z. Observe that these plots are converging to the
piecewise linear hat function
n
[x, y] on the three-direction grid defined by , with
the shifting of the hat function due to the use of an uncentered subdivision mask.
Four-direction Quadratic Box Splines
The piecewise linear hat function in the previous example is a continuous (i.e., C
0
)
function. Adding an extra copy of the direction vector
{1, 1} to the three direction
vectors
{1, 0}, {0, 1}, and {1, 1} for linear box splines yields a new set of four
direction vectors that defines a quadratic box spline. However, observe that
α == 2
for this case, in that removing {1, 0} and {0, 1} from leaves the two copies of the
vector
{1, 1} that together do not span the plane R
2
. Therefore, this quadratic box
spline is only
C
0
.
On the other hand, if we add a new vector in an independent direction—
say
{−1, 1}—to the direction vectors {1, 0}, {0, 1}, and {1, 1}, the resulting set of
direction vectors
{{1, 0}, {0, 1}, {1, 1}, {−1, 1}} defines a smooth box-spline scaling
50 CHAPTER 2 An Integral Approach to Uniform Subdivision
function, because α == 3. Via equation 2.16, the subdivision mask for this box
spline has the form
s
[x, y] = 4
(a,b)∈
1 + x
a
y
b
2
==
1
4
(1 + x)(1 + y)(1 + xy)(1 + x
−1
y).
Plotting the coefficients of s
[x, y] as a two-dimensional array yields
s
[x, y] == (x
−1
1xx
2
)
⎛
⎜
⎜
⎜
⎜
⎜
⎝
0
1
4
1
4
0
1
4
1
2
1
2
1
4
1
4
1
2
1
2
1
4
0
1
4
1
4
0
⎞
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎝
1
y
y
2
y
3
⎞
⎟
⎟
⎠
.
The four subdivision rules for this scheme correspond to taking convex combina-
tions of the entries of the vector
p
k−1
using the weights
0
1
4
1
4
1
2
,
1
4
1
2
0
1
4
,
1
4
0
1
2
1
4
,
1
2
1
4
1
4
0
.
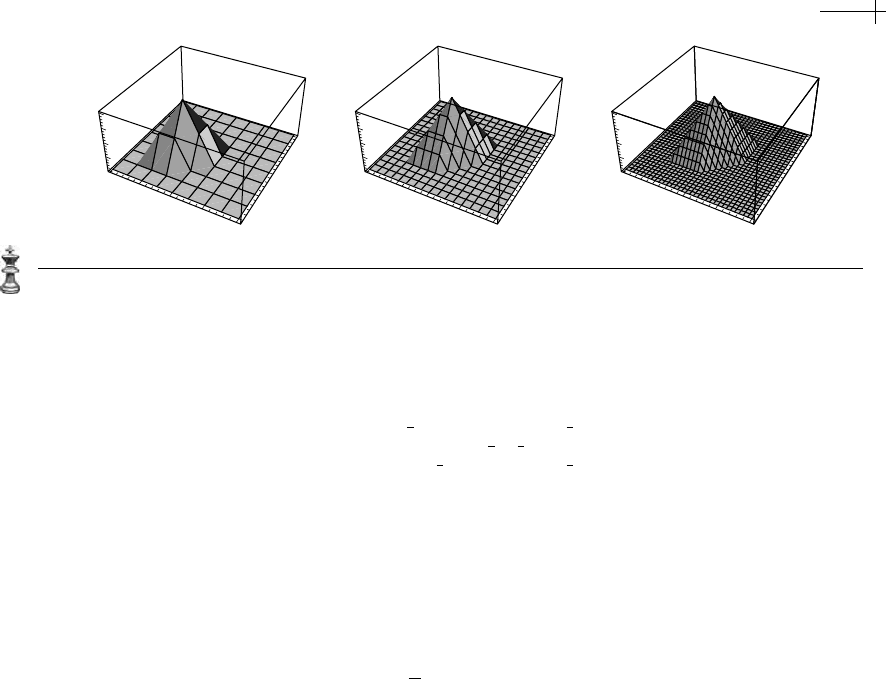
Figure 2.13 shows the results of three rounds of subdivision under this scheme,
applied to the generating function
p
0
[x, y] = 1. The resulting polyhedra are converg-
ing to the scaling function
n
[x, y]. This function, n
[x, y], is a piecewise quadratic
function supported over an octagon. Note that the integer translates of the scaling
function
n
[x, y] for this box spline are linearly dependent. In particular, choosing
the initial coefficients
p
0
for this box spline to satisfy p
0
[[ i , j]] = (−1)
i +j
yields the
function zero.
0
2
4
0
.4
.2
2
0
2
0
2
4
0
.4
.2
2
0
2
0
2
4
0
.4
.2
2
0
2
Figure 2.13 Three rounds of subdivision for the four-direction quadratic box-spline scaling function.

2.2 A Subdivision Scheme for Box Splines 51
Three-direction Quartic Box Splines
We conclude with an example of a box spline whose scaling function has continuous
second derivatives (i.e., is
C
2
). This box spline, the three-direction quartic, is defined
in terms of six direction vectors: the three direction vectors used in defining the
linear hat function, each repeated. Specifically, the set of direction vectors
has
the form
{{1, 0}, {1, 0}, {0, 1}, {0, 1}, {1, 1}, {1, 1}}. For this example, α == 4, and
therefore the resulting spline is
C
2
. According to equation 2.16, the subdivision
mask for the scheme has the form
s
[x, y] == 4
(a,b)∈
1 + x
a
y
b
2
=
1
16
(1 + x)
2
(1 + y)
2
(1 + xy)
2
.
Plotted in two dimensions, the coefficients of this subdivision mask have the form
s
[x, y] == (1xx
2
x
3
x
4
x
5
)
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
1
16
1
8
1
16
00
1
8
3
8
3
8
1
8
0
1
16
3
8
5
8
3
8
1
16
0
1
8
3
8
3
8
1
8
00
1
16
1
8
1
16
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
1
y
y
2
y
3
y
4
y
5
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
.
The four subdivision rules for this scheme correspond to taking convex combina-
tions of the entries of the vector
p
k−1
using the weights
⎛
⎜
⎜
⎝
1
16
1
16
0
1
16
5
8
1
16
0
1
16
1
16
⎞
⎟
⎟
⎠
,
1
8
3
8
0
0
3
8
1
8
,
⎛
⎜
⎜
⎝
1
8
0
3
8
3
8
0
1
8
⎞
⎟
⎟
⎠
,
3
8
1
8
1
8
3
8
.
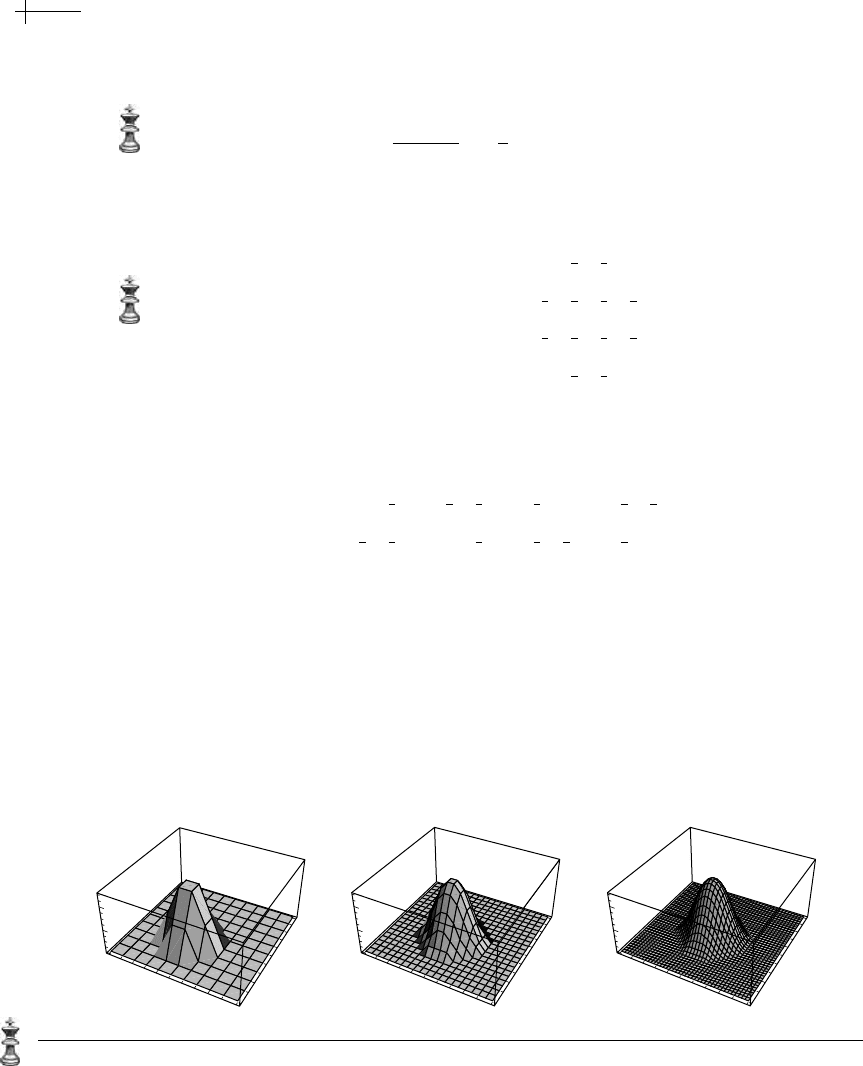
Figure 2.14 depicts three rounds of subdivision based on this scheme, starting
from the initial generating function
p
0
[x, y] = 1. The resulting plot is an approx-
imation of the basis function
n
[x, y], a piecewise quartic function defined over a
hexagon, with a support that is twice the size of the support hexagon for the hat
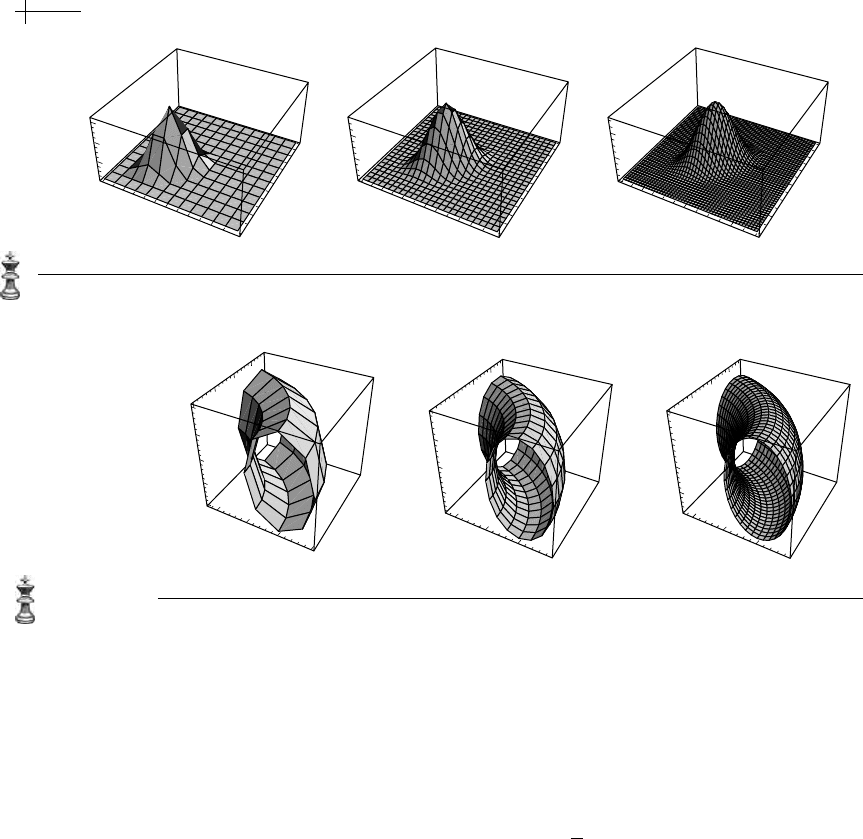
function. Figure 2.15 shows an example of a toroidal surface constructed using a
parametric version of the three-direction quartic box spline in which one coordinate
is treated as being periodic.
52 CHAPTER 2 An Integral Approach to Uniform Subdivision
0
2
4
0
.6
.4
.2
2
0
4
0
2
4
0
.4
.2
0
2
4
0
2
4
0
.4
.2
0
2
4
Figure 2.14 Three rounds of subdivision for the three-direction quartic box-spline basis function.
1
2
0
1
2
.5
0
.5
1
2
3
4
0
1
2
3
1
.5
0
.5
1
3
3
1
2
3
0
1
2
.5
0
.5
3
Figure 2.15 A parametric surface constructed using subdivision for a three-direction quartic box spline.
2.3 B-splines and Box Splines as Piecewise Polynomials
In the preceding examples, the plots of the box-spline scaling functions n
[x, y]
were constructed via subdivision. Starting with the initial generating function
p
0
[x, y] = 1, we applied several rounds of subdivision to compute p
k
[x, y] and plot-
ted the resulting coefficients of
p
k
on the grid
1
2
k
Z
2
. In practice, this approach of
computing discrete approximations is an extremely effective method for manipu-
lating box splines. However, occasionally it is useful to have access to the piecewise
polynomial representation of the box spline. For example, in finite element analysis,
knowing the exact value of the finite element basis functions at certain quadrature
points is very useful in constructing the inner product matrix associated with the
basis functions. Using the piecewise polynomial representation, the box spline can
be evaluated exactly at those quadrature points. Further, all of the results from clas-
sical functional analysis can be applied to the piecewise polynomial representation
to investigate the properties of a given box spline.

2.3 B-splines and Box Splines as Piecewise Polynomials 53
Attempting to construct the piecewise polynomial representation of a box-
spline scaling function based on the support and smoothness conditions for the
box spline is quite difficult. The number of polynomial pieces is large, and the lin-
ear relationships between coefficients for adjacent polynomial pieces are tedious to
construct. In this final section, we discuss an elegant technique for constructing the
piecewise polynomial representation for B-splines and box splines. For B-splines,
this technique expresses the basis functions
n
m
[x] as a linear combination of trun-
cated powers. For box splines, the scaling functions
n
[x, y] are expressed as a linear
combination of cone splines, the cross-sectional volumes of high-dimensional cones.
As we will see later, the differential approach to subdivision, introduced in Chap-
ter 4, is closely tied to these results.
2.3.1 B-splines as Combinations of Truncated Powers
In section 2.2.1, we expressed the B-spline basis function n
m
[x] as the cross-sectional
volume of the hypercube
H
m
. In this section, we consider the cross-sectional volume
c
m
[x] of a related cone and show that n
m
[x] can be expressed as a linear combination
of translates
c
m
[x − i].IfR
+
denotes the half-interval consisting of all non-negative
real numbers, the cone
(R
+
)
m
consists of those points {t
1
, ..., t
m
} such that 0 ≤ t
i
for
1 ≤ i ≤ m. Just as was done for hypercubes, we consider the cross-sectional volumes
of the form
c
m
[x] =
1
√
m
vol
m−1
{t
1
, ..., t
m
}∈(R
+
)
m
m
i =1
t
i
== x
. (2.18)
Because the interval H can be expressed as the difference of the half-interval R
+
and
its integer translate in the positive direction—that is, the interval
[0, 1) is the differ-
ence of the intervals
[0, ∞) and [1, ∞)—the hypercube H
m
can be decomposed into
an alternating sum of
2
m
integer translates of the cone (R
+
)
m
. This decomposition
induces an interesting relation between cross-sectional volumes of these objects:
the B-spline basis function
n
m
[x] and integer translates of the function c
m
[x].
For example, in Figure 2.10, a piecewise linear hat function could be viewed as
the cross-sectional length of a square
H
2
. In Figure 2.16, the square H
2
has been ex-
pressed as the alternating sum of four translates of the cone
(R
+
)
2
, each with a vertex
at the corner of the square and opening toward the right. The leftmost cone con-
tains the square. The top and bottom cones are subtracted from the leftmost cone,
leaving the square. The top and bottom cones overlap, forming the rightmost cone.
Adding this rightmost cone back accounts for this overlap and leaves the original
square.
