Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

34 CHAPTER 2 An Integral Approach to Uniform Subdivision

THEOREM

2.1

For all m > 1, the subdivision mask s

[x] for the B-spline basis function n

[x]

of order m satisfies the recurrence

[x] =

(1 + x)s

m−1

[x].

(2.6)

Proof The proof is inductive. Assume that the subdivision mask s

m−1

[x] encodes

the coefficients of the refinement relation for

m−1

[x]. Our task is to show

that the mask

(1 + x)s

m−1

[x] encodes the coefficients of the refinement

relation for

[x]. We begin with the inductive definition of

[x] as



m−1

[x − t] dt. Refining n

m−1

[x − t] via equation 2.4 yields the new in-

tegral







m−1

[[ i ]] n

m−1

[2(x − t) − i]



dt.

Reparameterizing via t →

t yields a new integral on the interval [0, 2]

scaled by a factor of

. Splitting this integral into two integrals on the

interval

[0, 1] and reindexing yields the equivalent integral







m−1

[[ i ]] + s

m−1

[[ i − 1]])n

m−1

[2x − t − i]



dt.

Moving the integral inside the sum yields



m−1

[[ i ]] + s

m−1

[[ i − 1]])



m−1

[2x − t − i]dt.

Finally, applying the definition of n

[2x − i] yields the desired scaling rela-

tion for

[x] as

[x] ==



m−1

[[ i ]] + s

m−1

[[ i − 1]])n

[2x − i].

The subdivision mask associated with this refinement relation is exactly

(1 + x)s

m−1

[x].

Starting from the base case s

[x] = 1 + x, we can now iterate this theorem

to obtain the subdivision masks for B-splines of higher order. In particular, the

2.1 A Subdivision Scheme for B-splines 35

subdivision mask for B-splines of order m has the form

[x] =

m−1

(1 + x)

. (2.7)

Due to this formula, the coefficients of the refinement relation for n

[x] are

simply the coefficients of the binomial expansion of

(1 + x)

scaled by a fac-

tor of

m−1

. Another technique for deriving the refinement relation for uniform

B-spline basis functions uses the definition of

[x] in terms of repeated continuous

convolution. Unrolling the recurrence

[x] = n

[x] ⊗ n

m−1

[x] leads to the formula

[x] =⊗

i =1

[x] =⊗

i =1

[2x] + n

[2x − 1] ).

Based on the linearity of convolution, this convolution of m + 1 functions can be

expanded using the binomial theorem into the sum of terms consisting of the

convolution of

m + 1 functions of the form n

[2x] or n

[2x−1]. Because these dilated

functions satisfy the recurrence

[2x] =

[2x] ⊗ n

m−1

[2x]),

these terms have the form

m−1

[2x−i], where 0 ≤ i ≤ m. Accumulating these terms

according to the binomial theorem yields the mask of equation 2.7.

2.1.3 The Associated Subdivision Scheme

Having computed the subdivision mask s

[x] for the B-spline basis function n

[x],

we can use the coefficients of

to construct a matrix refinement relation that

expresses translates of the basis function

[x] defined on the coarse grid Z in terms

of translates of the dilated function

[2x] on the finer grid

Z. This matrix rela-

tion has the form

[x] = N

[2x]S, where N

[x] is a row vector whose i th entry is

[x − i]. Just as in the linear case, this subdivision matrix S is a bi-infinite ma-

trix whose columns are two-shifts of the subdivision mask

. This two-shifting

arises from the fact that translating a refineable scaling function

[x] of the form



[[ i ]] n

[2x − i] by j units on Z induces a shift of 2j units in the translates of the

dilated scaling function

[2x] on

Z; that is,

[x − j] ==



[[ i ]] n

[2x − i − 2j]. (2.8)

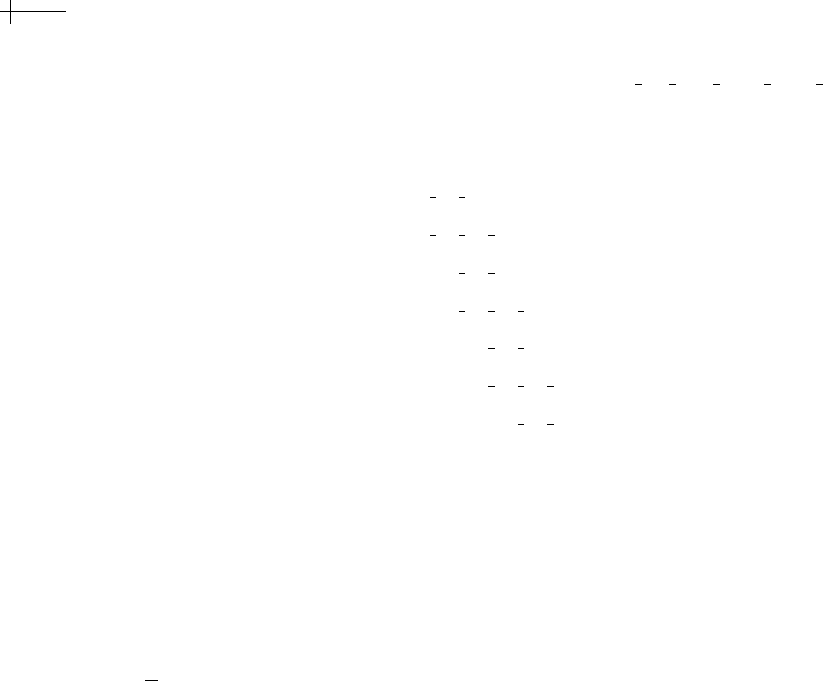
36 CHAPTER 2 An Integral Approach to Uniform Subdivision

Based on this formula, we observe that the ijth entry of the matrix S is s

[[ i − 2j]].

For example, the subdivision mask for cubic B-splines is

x +

The corresponding subdivision matrix

S has the form

⎛

⎜

⎝

.......

000.

00.

. 0

00.

. 0

0 .

. 00

0 .

. 00

. 000

.......

⎞

⎟

⎠

Given a B-spline p[x] expressed in vector form as N

[x]p

, this matrix refinement

relation implies that

p[x]

can also be expressed as N

[2x](Sp

). If we define a sub-

division process of the form

= Sp

k−1

the resulting vectors p

are the coefficients for the function p[x] defined on the grid

Z (i.e., p[x] = N

x]p

). Of course, in practice one should never actually con-

struct the subdivision matrix

S, because it is very sparse. Instead, the i th coefficient

can be computed as a linear combination of the coefficients in p

k−1

(using

equations 2.4 and 2.8):

[[ i ]] =



j ∈Z

[[ i − 2j]]p

k−1

[[ j ]] . (2.9)

If p

k−1

[x] and s

[x] are the generating functions associated with p

k−1

and s

, the

summation of pairwise products in equation 2.9 looks suspiciously like an expres-

sion for the coefficients of the product

[x]p

k−1

[x]. In fact, if the expression i − 2j

were replaced by i − j , equation 2.9 would indeed compute the coefficients of

[x]p

k−1

[x]. To model equation 2.9 using generating functions, we instead upsample

the coefficient vector

k−1

by introducing a new zero coefficient between each co-

efficient of

k−1

. The entries of the upsampled vector are exactly the coefficients of

the generating function

k−1

]. Because the j th coefficient of p

k−1

[x] corresponds

to the

(2j)th coefficient of p

k−1

], equation 2.9 can now be viewed as defining

2.1 A Subdivision Scheme for B-splines 37

the i th coefficient of the product s

[x]p

k−1

]. In particular, the analog in terms of

generating functions for the subdivision relation

= Sp

k−1

[x] = s

[x]p

k−1

]. (2.10)

To illustrate this subdivision process for uniform B-splines, we next consider

two examples, one linear and one cubic. For both examples, our initial coefficient

vector

will have the form {..., 0, 1, 3, 2, 5, 6, 0, ...}, where the non-zero entries

of this vector are indexed from

0 to 4. The corresponding generating function p

[x]

has the form 1 + 3x + 2x

+ 5x

+ 6x

. In the piecewise linear case, the subdivision

mask

[x] has the form

(1 + x)

. Applying equation 2.10 yields p

[x] of the form

[x] = s

[x]p

(1 + x)

(1 + 3x

+ 2x

+ 5x

+ 6x

+ x + 2x

+ 3x

+ 2x

+ 5x

11x

+ 6x

+ 3x

Subdividing a second time yields p

[x] = s

[x]p

], where p

[x] has the form

(1 +x)



+ x

+ 2x

+ 3x

+ 2x

+ 5x

11x

+ 6x

+ 3x



Using the technique of Chapter 1, we plot the

i th coefficient of the generating

function

[x] at the grid point x ==

. Figure 2.7 shows plots of the coefficients of

[x], p

[x], and p

[x] versus the grids Z,

Z, and

Z, respectively. We next

repeat this process for cubic B-splines using the subdivision mask

[x] =

(1 + x)

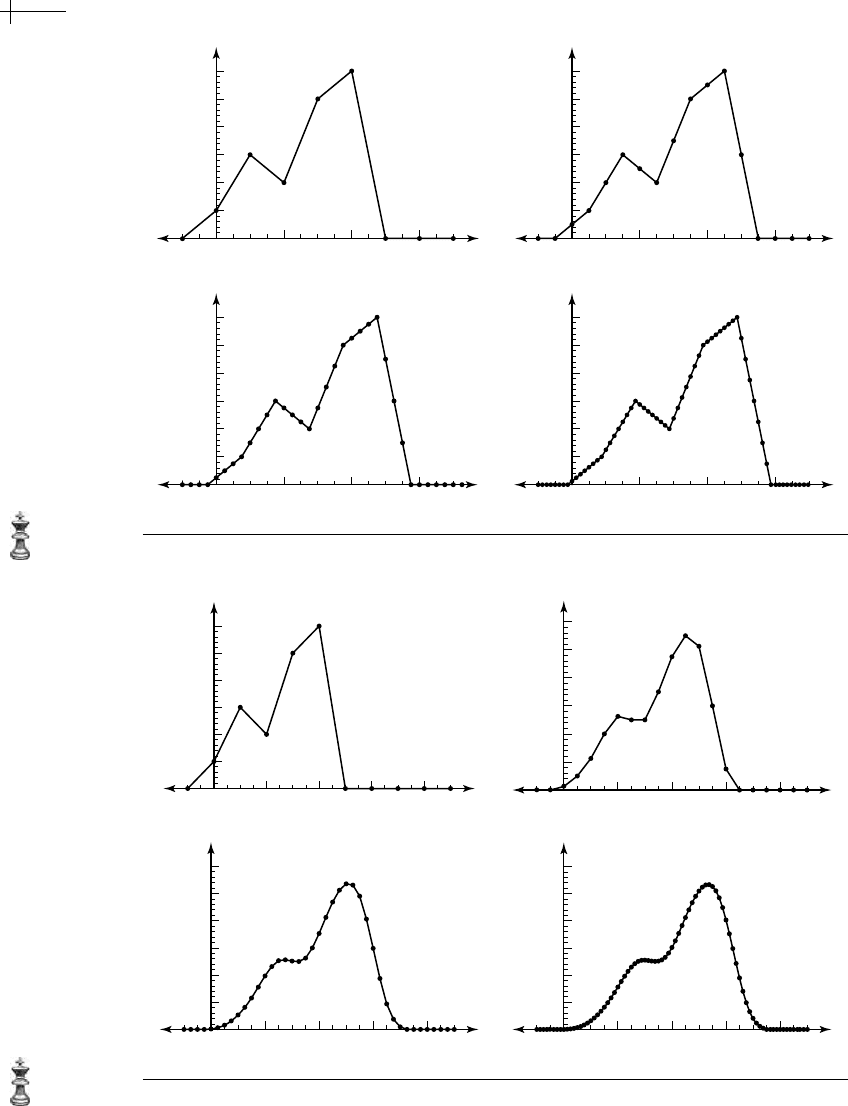
Figure 2.8 shows plots of the coefficients of

[x], p

[x], and p

[x] versus the

grids

Z, and

Z, respectively, where p

[x] = s

[x]p

k−1

The cubic B-spline

p[x] of Figure 2.5 was supported over the interval [0, 8].In

Figure 2.8, the polygons defined by the vector

appear to be converging to this

function

p[x] as k →∞. Note that the polygons in this figure shift slightly to the

right during each round of subdivision. This behavior is due to the fact that the sub-

division mask

(1 + x)

involves only non-negative powers of x; each multiplication

by this mask shifts the resulting coefficient sequence to the right. To avoid this

shifting, we can translate the basis function

[x] such that it is supported on the in-

terval

[−

]. The effect of the subdivision mask s

[x] is to multiply it by a factor of

−

. The resulting subdivision mask is now centered (as in equation 2.1). As a result,

the polygons corresponding to the vectors

no longer shift during subdivision.

For linear B-splines that are centered, it is clear that the coefficients of

interpolate the values of p[x] on the grid

Z, in that the basis function n

[x] has

38 CHAPTER 2 An Integral Approach to Uniform Subdivision

246

Figure 2.7 Three rounds of subdivision for a linear B-spline (m == 2).

2468

Figure 2.8 Three rounds of subdivision for a cubic B-spline (m == 4).

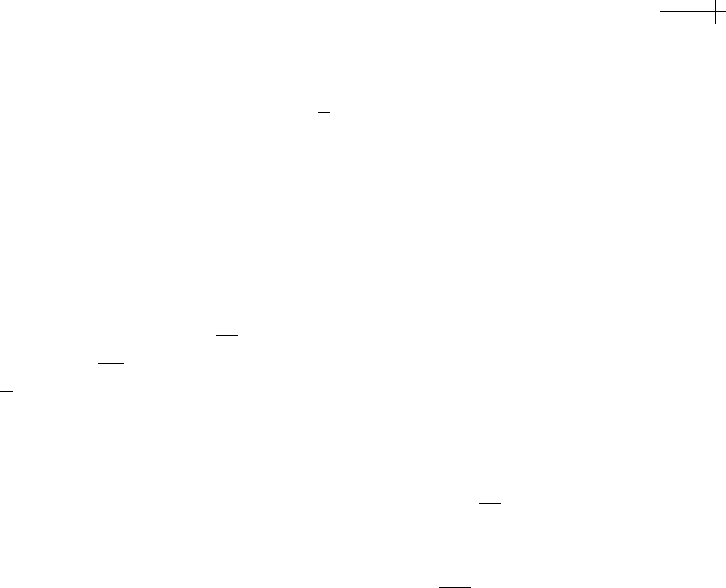
2.1 A Subdivision Scheme for B-splines 39

value 1 at x == 0 and is zero at the remaining integer knots. However, higher-order

B-splines are not interpolatory (i.e., their limit curves do not pass through the

coefficients of

plotted on the grid

Z). For now, the convergence of the vectors

to the actual values of p[x] as k →∞is simply assumed. For those interested in a

proof of this fact, we suggest skipping ahead to Chapter 3, where this question is

considered in detail.

This subdivision scheme for B-splines was first documented by Chaikin [18]

(for the quadratic case) and by Lane and Riesenfeld [93] (for the general case). Lane

and Riesenfeld described a particularly elegant implementation of this subdivision

method based on the factorization of

[x] in Theorem 2.1. The subdivision mask

[x] can be written as 2(

1+x

)

. Thus, given a set of coefficients p

k−1

defined on a

coarse grid

k−1

Z, we can compute a set of coefficients p

defined on the fine grid

Z as follows:

■

Construct the generating function p

k−1

[x] from p

k−1

. Upsample p

k−1

[x] to

obtain

k−1

]. Set p

[x] = 2p

k−1

■

Update p

[x] m times via the recurrence p

[x] = (

1+x

[x].

■

Extract the coefficients p

of the resulting generating function p

[x].

In geometric terms, each multiplication of

[x] by

(1+x)

corresponds to computing

the midpoints of adjacent vertices of the control polygon

. Thus, a single round

of subdivision for a B-spline of order

m can be expressed as upsampling followed

m rounds of midpoint averaging. Figure 2.9 shows an example of a single round

of subdivision for cubic B-splines implemented in this manner.

In practice, using generating functions to implement subdivision is inefficient.

A better method is to observe that the coefficient sequence for the product

[x]p

k−1

] is simply the discrete convolution of the sequence s

and the up-

sampled sequence

k−1

. Using an algorithm such as the Fast Fourier Transform

(FFT), the discrete convolution of these two coefficient sequences can be com-

puted very quickly. (See Cormen, Leiserson, and Rivest [27] for more information

on the FFT.) More generally, upsampling and midpoint averaging can be viewed as

simple filters. Used in conjunction with wiring diagrams, these filters are a useful

tool for creating and analyzing uniform subdivision schemes. An added benefit of

the filter approach is that it is compatible with the filter bank technology used

in constructing wavelets and in multiresolution analysis. Strang and Nguyen [150]

give a nice introduction to the terminology and theory of filters. Guskov et al. [69],

Kobbelt and Schr

oder [87], and Kobbelt [84] give several examples of using filter

technology to construct subdivision schemes.

40 CHAPTER 2 An Integral Approach to Uniform Subdivision

246

Figure 2.9 One round of cubic B-spline subdivision expressed as upsampling (top right) followed by four

rounds of midpoint averaging.

2.2 A Subdivision Scheme for Box Splines

In the previous section, B-spline basis functions were defined via repeated integra-

tion. Although this definition has the advantage that it is mathematically succinct,

it fails to deliver much geometric intuition about why B-spline basis functions

possess such a simple refinement relation. In this section, we give a more intuitive

geometric construction for these basis functions. Using this geometric construction,

the possibility of building analogs to B-splines in higher dimensions becomes im-

mediately clear. These analogs, the box splines, are simply cross-sectional volumes

of high-dimensional hypercubes. For the sake of notational simplicity, we restrict

our investigation of box splines to two dimensions. However, all of the results that

appear in this section extend to higher dimensions without any difficulty. A good

source for most of the material that follows is the book by De Boor et al. [40].

2.2 A Subdivision Scheme for Box Splines 41

2.2.1 B-spline Basis Functions as Cross-sectional Volumes

We begin with a simple geometric construction for the B-spline basis function of

order

m as the cross-sectional volume of an m-dimensional hypercube. Given an

interval

H = [0, 1),weletH

denote the m-dimensional hypercube consisting of all

points

, ..., t

} such that 0 ≤ t

< 1 for 1 ≤ i ≤ m. Now, consider a function n[x]

satisfying the equation

n[x] =

√

vol

m−1



, ..., t

}∈H





i =1

== x



, (2.11)

where vol

m−1

[B] is the (m − 1)-dimensional volume of the set B. For a particular

value of

x, n[x] returns the (m − 1)-dimensional volume of the intersection of the

m-dimensional hypercube H

and the (m − 1)-dimensional hyperplane



i =1

== x.

(The extra factor of

√

normalizes n(x) to have unit integral.)

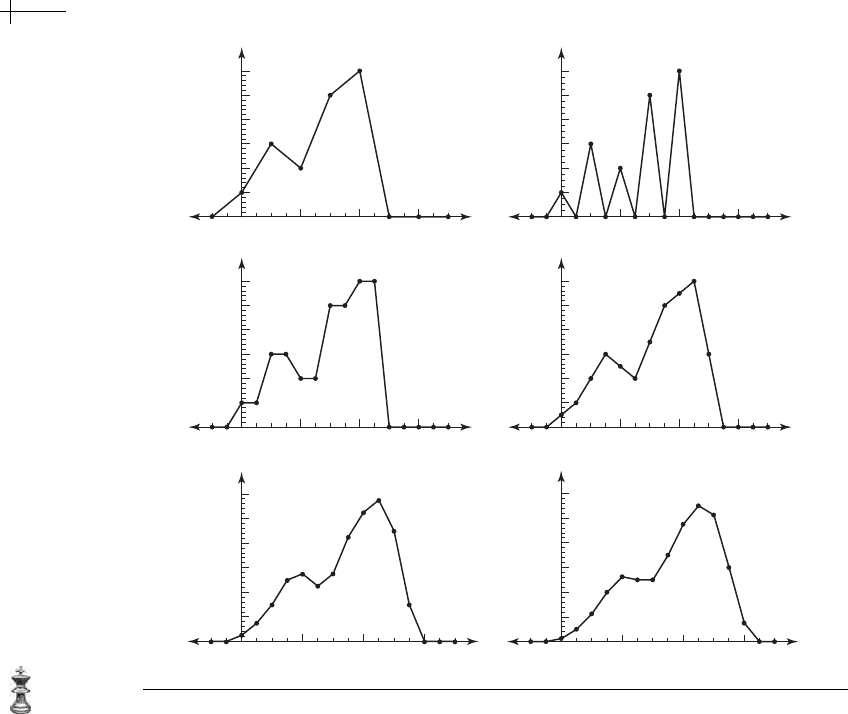
The left-hand portion of Figure 2.10 illustrates this construction for

m == 2.

At the top of the figure is the unit square

. At the bottom of the figure is a

plot of

n[x], the length of the line segment formed by intersecting the vertical line

+ t

== x with the square H

. Observe that n[x] is exactly the piecewise linear

hat function. The right-hand portion of Figure 2.10 illustrates this construction for

m = 3. At the top of the figure is the unit cube H

. At the bottom of the figure is a

plot of

n[x], the area of the polygon formed by intersecting the plane t

+ t

== x

(orthogonal to the x axis) with the cube H

. Again, n[x] looks remarkably like the

quadratic B-spline basis function.

2 10123

(a) (b)

Figure 2.10 (a) Linear and (b) quadratic B-spline basis functions as cross-sectional volumes of the hyper-

cubes H

and H

42 CHAPTER 2 An Integral Approach to Uniform Subdivision

Because the vertices of H

project onto integer points on the x axis, the function

n[x] is a piecewise polynomial function of degree m −1, with knots at Z. In fact, the

function

n[x] generated by the cross-sectional volume of H

is exactly the B-spline

basis function

[x]. The following theorem shows that cross-sectional volumes

used in defining n[x] satisfy a recurrence identical to that of equation 2.3.

THEOREM

2.2

The B-spline basis function

[x] of equation 2.3 satisfies equation 2.11;

that is,

[x]

√

vol

m−1



, ..., t

}∈H





i =1

== x



Proof The proof proceeds by induction on m. The base case of m == 1 holds

by inspection. If we assume that

m−1

[x] satisfies the volume definition of

equation 2.11,

m−1

[x] =

√

m − 1

vol

m−2



, ..., t

m−1

}∈H

m−1



m−1



i =1

== x



our task is to show that n

[x] also satisfies equation 2.11. To complete

this induction, we observe that the

(m − 1)-dimensional volume on the

right-hand side of equation 2.11 satisfies the recurrence:

√

vol

m−1



, ..., t

}∈H





i =1

== x



(2.12)



√

m − 1

vol

m−2



, ..., t

m−1

}∈H

m−1



m−1



i =1

== x − t



The various square roots in this expression normalize the integral of the

(m−2)-dimensional volumes to agree with the (m−1)-dimensional volume.

Applying our inductive hypothesis to the right-hand side of this equa-

tion yields

√

vol

m−1



, ..., t

}∈H





i =1

== x





m−1

[x − t

] dt

. (2.13)

Applying the inductive definition of n

[x] from equation 2.3 completes the

proof.

2.2 A Subdivision Scheme for Box Splines 43

This idea of constructing B-spline basis functions as the cross-sectional volumes of

a higher-dimensional polytope appeared as early as 1903 in Sommerfeld [142] and

was popularized by Curry and Sch

onberg in [28]. (Curry and Sch

onberg actually

suggested using a simplex in place of

Given this geometric construction for

[x], the refinement relation for n

[x]

has an elegant interpretation. Consider the effect of splitting the hypercube

into 2

subcubes by splitting the interval H into the subintervals [0,

) and [

, 1).

Because all of these new subcubes are scaled translates of the original hypercube

, their cross-sectional volumes are multiples of integer translates of the dilated

cross-sectional volume

[2x].

For example, the left-hand side of Figure 2.11 illustrates the case of

m == 2.

At the top, the square

has been split into four subsquares. At the bottom is

a plot of the cross-sectional lengths of each of these subsquares. (Note that the

cross-sectional lengths for subsquares with the same projection onto

x have been

summed.) Because cross-sectional length is halved when the square

is split, the

cross-sectional lengths satisfy the recurrence

[x] ==

[2x] + n

[2x − 1] +

[2x − 2].

This equation is exactly the refinement relation for linear B-splines. The right-hand

side of Figure 2.11 illustrates the case of

m == 3. At the top, the cube H

has been

split into eight subcubes. At the bottom is a plot of the cross-sectional areas of

each of these subcubes. (Note that the cross-sectional areas for subcubes with the

2 101234

2 1012345

(a) (b)

Figure 2.11 Subdividing (a) linear and (b) quadratic basis functions by splitting the hypercubes H

and H