Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

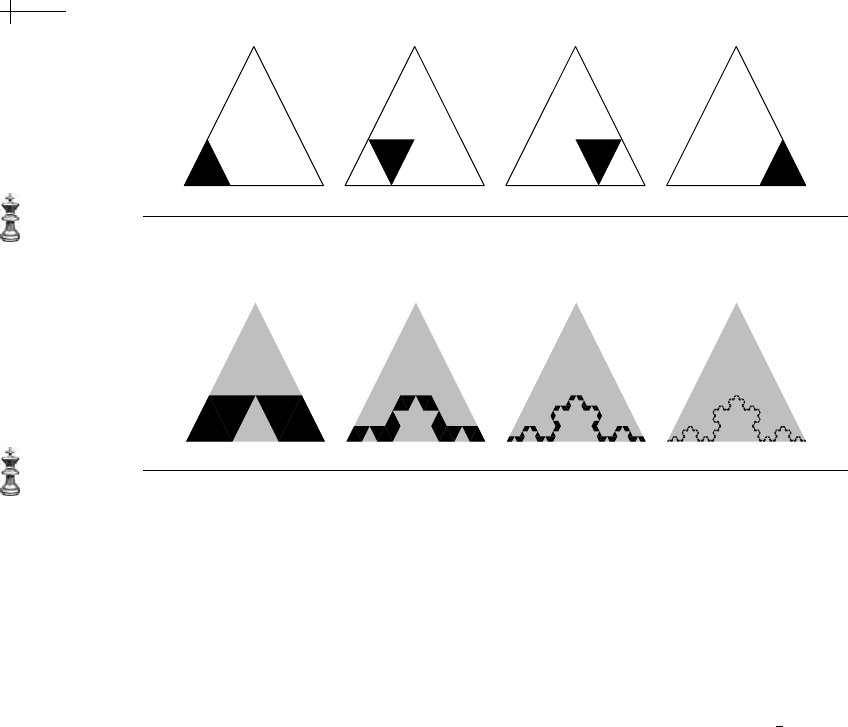
14 CHAPTER 1 Subdivision: Functions as Fractals

Figure 1.10 The four afﬁne transformations used in deﬁning the Koch snowf lake.

Figure 1.11 Progression approximations of the Koch curve.

Each of these four transformations maps the base triangle to one of the four image

triangles shown in Figure 1.10. The two transformations on the left map the upper

vertex of the base triangle to a point two-thirds of the way down the upper left

edge of the base triangle. The transformations on the right map the upper vertex

of the base triangle to a point two-thirds of the way down the upper right edge of

the base triangle.

Because each of these affine transformations is contractive (with

β ==

), there

exists a fractal limit to the process

= Sp

k−1

. As before, the set of transformations

is repeatedly applied to the base triangle

until the size of the children reaches a

desired resolution. Figure 1.11 depicts the four applications of the transformation

to the gray parent triangle

. Again, we observe that the fractal limit is a collage

of four affine copies of itself, placed along the base of the triangle

according to

the four transformations in

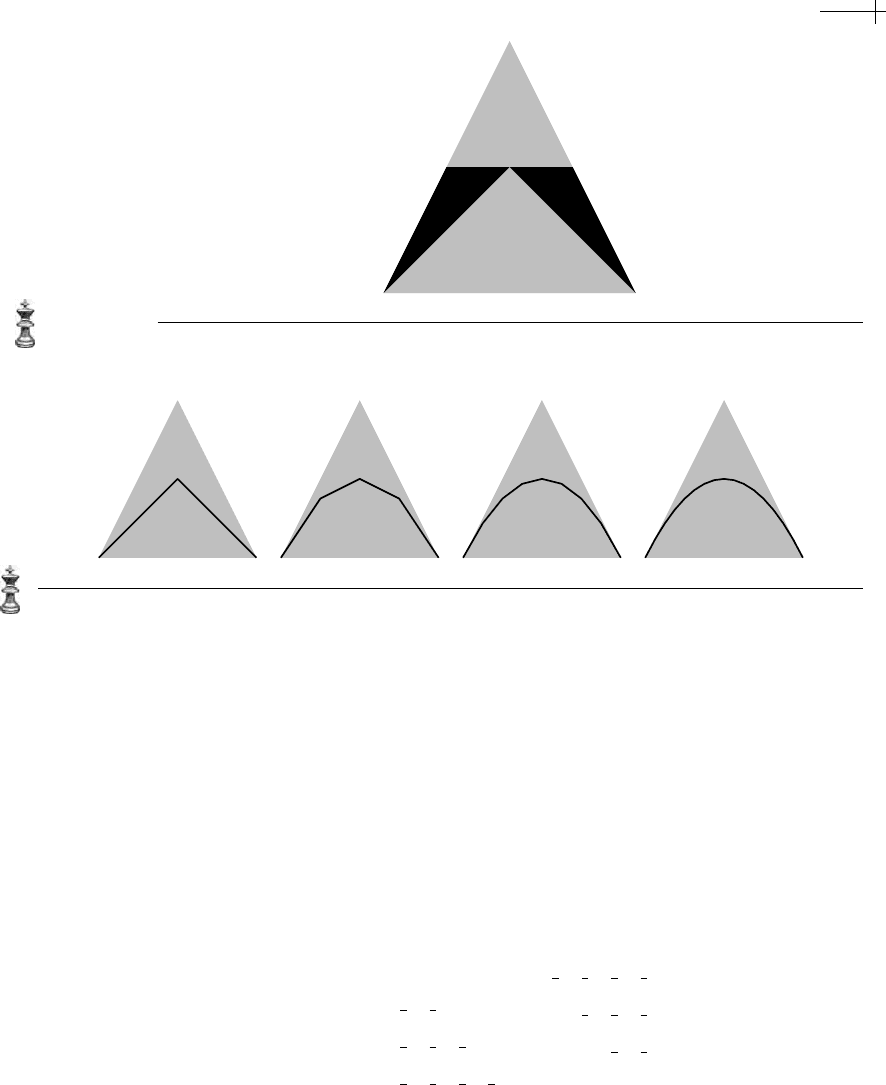
In the previous example, we started the fractal rendering process with just one

base triangle. A neat trick can be applied to close the Koch curve into an actual

snowflake. We can apply one round of the fractal process for the Sierpinski triangle

to a single, initial triangle. The result is three smaller triangles we then use as the

initial geometry for the fractal process associated with the Koch curve. Figure 1.12

shows the three triangles resulting from one round of the fractal process for the

Sierpinski triangle. The result of applying the Koch transformations to these three

1.2 Fractals 15

Figure 1.12 The Koch snowﬂake.

triangles repeatedly is shown in black in Figure 1.12 and resembles the outline of a

snowflake.

1.2.4 B´ezier Curves

As a final example, we develop a fractal process for the class of shapes first encoun-

tered in section 1.1, B

ezier curves. Recall that a B

ezier curve

p[x] was defined in

equations 1.1 and 1.2 as the convex combination of a set of points

p. The weights

used for this combination were the values of the Bernstein basis functions

[x].

Our goal now is to construct two affine transformations that form a collage for

this B

ezier curve. These affine transformations can be derived from the subdivision

algorithm for B

ezier curves, the de Casteljau algorithm. This subdivision algorithm

splits the control polygon for an entire B

ezier curve

p[x]

into two control polygons:

one for the first half of the curve, corresponding to

x ∈ [0,

], and one for the second

half of the curve, corresponding to

x ∈ [

, 1].

Given a vector of points

p, this algorithm recursively computes a related tri-

angular array of points 

p. In the base case, the base of the triangular array p[[i , i]] is

initialized to

p[[ i ]] for 0 ≤ i ≤ m.For0 ≤ i < j ≤ m, the points p[[i , j]] are defined by

the recurrence



p[[i, j]] =

p[[i, j − 1]] +

p[[i + 1, j]]. (1.5)

For m == 3, this recurrence has the tabular form shown in Figure 1.13. The

beauty of this algorithm is that the control points for the two new control polygons

lie on the lateral edges of Figure 1.13. In particular, the control polygon for the

16 CHAPTER 1 Subdivision: Functions as Fractals

冀1,2冁

冀1,3冁p

冀0,2冁

冀0,3冁

冀1,1冁

冀0,1冁

冀0,0冁

冀2,2冁

冀2,3冁

冀3,3冁

Figure 1.13 The de Casteljau algorithm for cubic B ´ezier curves.

restriction of p[x] to the interval [0,

] is {p[[0, 0]], p[[0, 1]], ..., p[[0, m]]}. Likewise, the

control polygon for the restriction of

p[x] to the interval [

, 1] is {p[[0, m]], p[[1, m]], ...,

p[[m, m]]}. A powerful tool for understanding the behavior (and correctness) of the

de Casteljau algorithm is blossoming, credited to Ramshaw [127]. Seidel [140] gives

a nice introduction to this topic.

Based on the de Casteljau algorithm, we can express B

ezier curves as iterated

affine transformations. For quadratic B

ezier curves (i.e.,

m == 2), one affine trans-

formation maps the polygon

p to the polygon {p[[0, 0]], p[[0, 1]], p[[0, 2]]}. The second

affine transformation maps the polygon

p to the polygon {p[[0, 2]], p[[1, 2]], p[[2, 2]]}.

Based on equation 1.5, the two

3 ×3 matrices defining these transformations have

the form

S =

⎧

⎪

⎨

⎪

⎩

⎛

⎜

⎝

100

⎞

⎟

⎠

⎛

⎜

⎝

001

⎞

⎟

⎠

⎫

⎪

⎬

⎪

⎭

One application of this set of transformations to an initial triangle yields two finer

triangles built from the midpoints of the legs of the base triangle, as well as the

center of these two midpoints. Figure 1.14 shows this construction applied to the

gray parent triangle.

Because both of these transformations are contractive (with

β =

), iteratively

applying this pair of affine transformations leads to an elegant multiresolution al-

gorithm for rendering B

ezier curves. The visual appearance of the plots produced

by this method can be improved by drawing only the line segment connecting the

first and last vertex of each triangle in

. Due to the structure of the two affine

transformations, the result of

n iterations of p

= Sp

k−1

is a continuous sequence of

1.2 Fractals 17

Figure 1.14 One round of an iterated afﬁne transformation based on the quadratic de Casteljau algorithm.

Figure 1.15 Four rounds of an iterated afﬁne transformation converging to a quadratic B ´ezier curve.

line segments whose 2

+ 1 vertices lie on the B

ezier curve. Figure 1.15 shows

the progression of this rendering algorithm for a quadratic B

ezier curve.

Higher-degree B

ezier curves can also be constructed as the limit of iterated

affine transformations. To generate a B

ezier curve of degree

m, the set of transfor-

mations

S consists of a pair of (m+1)×(m+1) matrices defined via the de Casteljau

algorithm. These matrices can be viewed as defining a pair of

m-dimensional affine

transformations. In the case of planar B

ezier curves, these

m-dimensional transfor-

mations are then applied to a degenerate

m-dimensional simplex (i.e., an (m + 1)-

gon) that lies entirely in the plane. For example, cubic B

ezier curves have a pair of

associated transformation matrices of the form

S =

⎧

⎪

⎨

⎪

⎩

⎛

⎜

⎝

1000

⎞

⎟

⎠

⎛

⎜

⎝

0001

⎞

⎟

⎠

⎫

⎪

⎬

⎪

⎭

18 CHAPTER 1 Subdivision: Functions as Fractals

Figure 1.16 One round of an iterated afﬁne transformation based on the cubic de Casteljau algorithm.

Figure 1.17 Four rounds of an iterated afﬁne transformation converging to a cubic B ´ezier curve.

Figure 1.16 shows the result of applying this transformation to an initial quadrilat-

eral (a degenerate tetrahedron). Note that the vertices of the black quadrilaterals

lie at the various combinations of midpoints of the gray quadrilateral. Given the

gray base quadrilateral

, iterating p

= Sp

k−1

yields a continuous sequence of

line segments that approximates the associated cubic B

ezier curve. Figure 1.17

shows several rounds of these transformations applied to the cubic control polygon

of Figure 1.7. For those readers interested in more information on extensions of

this approach to curve subdivision, we recommend two papers by Micchelli and

Prautzsch [104, 105].

1.3 Subdivision

The first part of this chapter described two popular techniques for representing

complex shapes: explicit functions and fractal procedures. When describing shapes

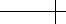
1.3 Subdivision 19

with functions, piecewise polynomials are a particularly common and practical

choice. Piecewise polynomial functions provide a convenient and efficient method

of defining smooth curved shapes. In addition, the mathematics of the resulting

geometry is well understood. On the other hand, iterated affine transformations

define a richer class of shapes using the very simple concept of iterative transforma-

tions. However, analyzing the behavior of the final limit shapes can be extremely

challenging.

Subdivision captures the best of both methods. Using subdivision, a curve is

defined as the limit of an increasingly faceted sequence of polygons. Each poly-

gon is related to a successor by a simple linear transformation that provides an

increasingly accurate approximation to the final limit curve. In most applications,

a sufficiently dense polygon can be used in place of the final limit curve without

any noticeable error.

Remarkably, many of the traditional shapes used in geometric design can be

defined using subdivision. As the previous section illustrated, B

ezier curves have a

very simple subdivision method, the de Casteljau algorithm. The solutions to many

variational problems and partial differential equations can also be expressed using

subdivision. Moreover, many new shapes useful in geometric design are defined

only in terms of subdivision. The rest of this section introduces the basic mechanics

of subdivision in terms of a simple example: piecewise linear splines.

1.3.1 Piecewise Linear Splines

Our approach is to introduce piecewise linear splines in terms of their polynomial

definition and later propose a functional analog of the collage property. This prop-

erty leads to a simple multiresolution rendering method for piecewise linear splines.

Consider the piecewise linear function of the form

n[x] = c[x + 1] − 2c[x] + c[x − 1],

where c[x] is the truncated linear function that is x if x ≥0 and zero if x < 0.

For

x /∈ [−1, 1], the function n[x] is identically zero. At x == 0, n[x] is exactly one.

Elsewhere,

n[x] varies linearly. Therefore, n[x] is the unit hat function. Figure 1.18

shows plots of

c[x] and n[x], respectively.

Replacing the parameter

x in the function n[x] by x − i has the effect of translat-

ing the unit hat function

i units to the right. Figure 1.19 plots the functions n[x −i]

over the parameter range x ∈ [−2, 2] for various integer values of i . Now, consider

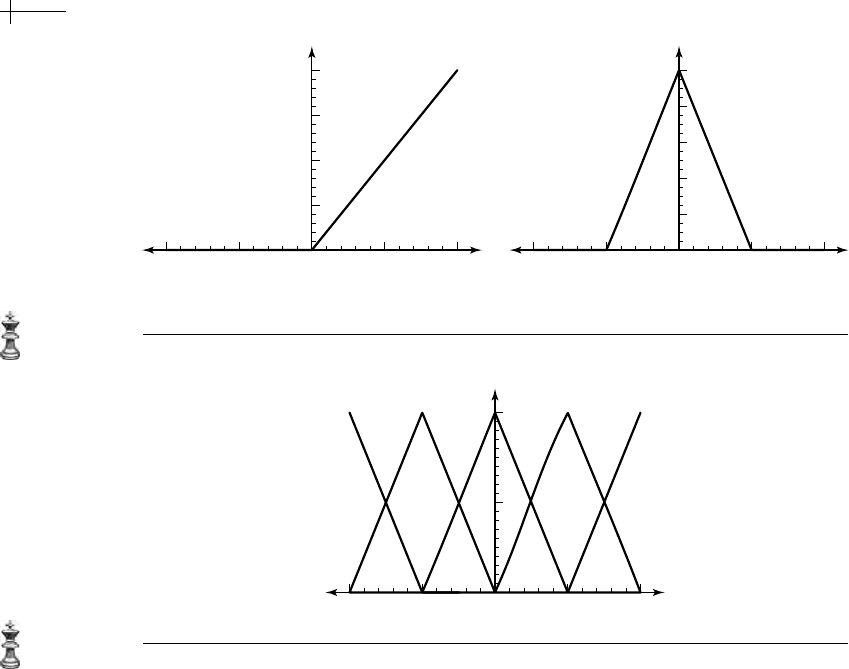
20 CHAPTER 1 Subdivision: Functions as Fractals

2 112

1.5

2 112

(a) (b)

Figure 1.18 The functions c[x] (a) and n[x] (b).

2 112

Figure 1.19 Several translates of the unit hat function.

a new function p[x] constructed as a linear combination of translated hat functions,

that is,

p[x] having the form

p[x] =

∞



i =−∞

p[[ i ]] n[x − i], (1.6)

where p[[ i ]] is the i th element of a column vector of coefficients p. Again, this

expression can be written in vector form as

p[x] = N [x]p, where N [x] is a row vector

whose

i th entry is n[x − i].

Due to the piecewise definition of

n[x], the breakpoints (called knots) between

the linear pieces of the function

p[x] lie at the integers Z. Due to the uniform spacing

of these knots,

p[x] is a uniform spline. For uniform splines, the function n[x] is often

referred to as the scaling function associated with the spline. If the translates of the

scaling function

n[x − i] are linearly independent, these scaling functions are basis

functions for the space of splines in equation 1.6. Much of the first part of this book

considers the problem of subdivision for uniform splines.

1.3 Subdivision 21

2 112

Figure 1.20 Several translates of dilates of the unit hat function.

To develop a multiresolution representation for linear splines, we next con-

sider the relationship between splines with knots at the integers

Z and splines with

knots at the half-integers

Z. Note that replacing the parameter x by 2x has the

effect of dilating (i.e., expanding) the coordinate axis. Applying this transformation

to the function

n[x] yields a new hat function n[2x] that has been compressed by

a factor of two and that is supported on the interval

[−

]. Figure 1.20 displays

translates of dilated scaling functions of the form

n[2x − i], plotted over the range

x ∈ [−2, 2]. Note that there are twice as many scaling functions as before. More-

over, these dilated scaling functions are centered over the half-integers

Z, whereas

the original scaling functions are centered over the integers

Z. Finally, the range in

which a scaling function

n[2x − i] is non-zero is just half as wide as for the origi-

nal scaling functions

n[x − i]. These translates n[2x − i] of the dilated hat function

form a basis for the space of piecewise linear functions with knots at the half-

integers

In the previous section on fractals, the collage property stated roughly that a

fractal could be expressed as the union of a collection of affine copies of itself. In our

current functional setting, the analog of this property is to express the hat functions

n[x] as linear combination of translated dilates n[2x − i]. Recalling our definition of

n[x] in terms of c[x] and the fact that c[2x] = 2c[x], it is easy to verify that the hat

function

n[x] satisfies the refinement relation

n[x] ==

n[2x + 1] + n[2x] +

n[2x − 1].

(1.7)

Recurrences of this type are sometimes referred to as two-scale relations, in that they

relate scaling functions defined on two consecutive scales. The refinement relation

22 CHAPTER 1 Subdivision: Functions as Fractals

for a scaling function n[x] is the analog of a collage for a fractal and provides the key

ingredient necessary for subdivision. Note that a variant of this refinement relation

also holds for translates of the scaling function

n[2

x] on the grid

1.3.2 Subdivision for Piecewise Linear Splines

Given this refinement relation, we can now construct the subdivision scheme for

piecewise linear splines. Consider a linear spline

p[x] with knots on Z. The spline

p[x] can be written as a linear combination of hat functions n[x − i] on the coarse

grid

Z. In vector form, this fact can be expressed as

p[x] = N [x]p

, (1.8)

where N [x] is a row vector whose i th entry is the function n[x−i]and p

is a column

vector whose entries are the values of

p[x] on Z. Due to equation 1.7, p[x] can also

be written as a linear combination of hat functions

n[2x −i], with knots on the fine

grid

Z. In vector form, this linear combination can be expressed as

p[x] = N [2x]p

, (1.9)

where p

is a vector whose entries correspond to the values of p[x] on

Z. Given

these two expressions, our task is to find the change of basis matrix relating

and

. Rewriting equation 1.7 in vector form, the coarse scaling functions N [x] can be

expressed as a linear combination of the next finer scaling functions

N [2x] via a

change of basis matrix

S satisfying

N [x] == N [2x]S. (1.10)

This subdivision matrix, S, has entries that depend only on the coefficients of

the refinement relation. In particular, the

i th column of S consists of the coefficients

attached to the entries of

N [2x] that reproduce the scaling function n[x−i]. For piece-

wise linear splines, this column vector has exactly three non-zero entries

{

, 1,

with corresponding row indices

{2i −1, 2i , 2i +1}. Note that each time i is increased

by one, the corresponding row indices of the non-zero entries are shifted by two.

The resulting matrix

S has the property that each of its columns is a two-shift of

a single fundamental vector

s. In particular, the i th entry s[[i]] is the coefficient of

the function

n[2x − i] on the right-hand side of equation 1.7. Such matrices whose

columns are two-shifts of a fundamental vector are known as two-slanted matrices.In

1.3 Subdivision 23

this example, S can be viewed as a two-slanted matrix whose columns are two-shifts

of the common sequence

{

, 1,

}. In particular, equation 1.10 expands into

⎛

⎜

⎝

n[x + 2]

n[x + 1]

n[x]

n[x − 1]

n[x − 2]

⎞

⎟

⎠

⎛

⎜

⎝

n[2x + 3]

n[2x + 2]

n[2x + 1]

n[2x]

n[2x − 1]

n[2x − 2]

n[2x − 3]

⎞

⎟

⎠

⎛

⎜

⎝

.......

000.

. 01000.

. 0

00.

. 00100.

. 00

0 .

. 00010.

. 000

.......

⎞

⎟

⎠

(Note that the dots are used to emphasize that the vectors and matrices of this re-

lation are bi-infinite.) Substituting the right-hand side of equation 1.10 into equa-

tion 1.8 yields

p[x] == N [2x](Sp

). Because the functions of N [2x] are linearly inde-

pendent,

= Sp

. Given that equation 1.10 holds, the following theorem makes

these observations precise.

THEOREM

1.1

Let the matrix refinement relation of equation 1.10 hold (i.e., N [x] =

N [2x]S

). If function p[x] has the form p[x] = N [x]p

, then p[x] == N [2

x]p

where

= Sp

k−1

. (1.11)

Proof Observe that replacing x by 2

k−1

x in equation 1.10 yields a matrix refinement

relation for basis functions on

k−1

Z and

Z (i.e., N [2

k−1

x] = N [2

x ]S).

Proceeding inductively, we assume that

p[x] = N [2

k−1

x]p

k−1

. Replacing

N [2

k−1

x] by the right-hand side of this matrix refinement relation yields

p[x] = N [2

x](Sp

k−1

). Given that the functions of N [2

x ] are linearly inde-

pendent, equation 1.11 holds.

Given an initial vector of coefficients p

, we can apply equation 1.11 to generate

a sequence of new vectors

. Because the entries of p

are coefficients of hat

functions taken on the grid

Z, plotting the i th entry of p

at x ==

gives a good