Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

4 CHAPTER 1 Subdivision: Functions as Fractals

difficult. For example, consider the piecewise polynomial function n[x] whose value

has the form

n[x] =

⎧

⎪

⎨

⎪

⎩

0 if x ∈ [−∞, 0],

if x ∈ [0, 1],

− 2x + 2x

−

if x ∈ [1, 2],

−

+ 10x − 4x

if x ∈ [2, 3],

−

(−4 + x)

if x ∈ [3, 4],

0 if x ∈ [4, ∞].

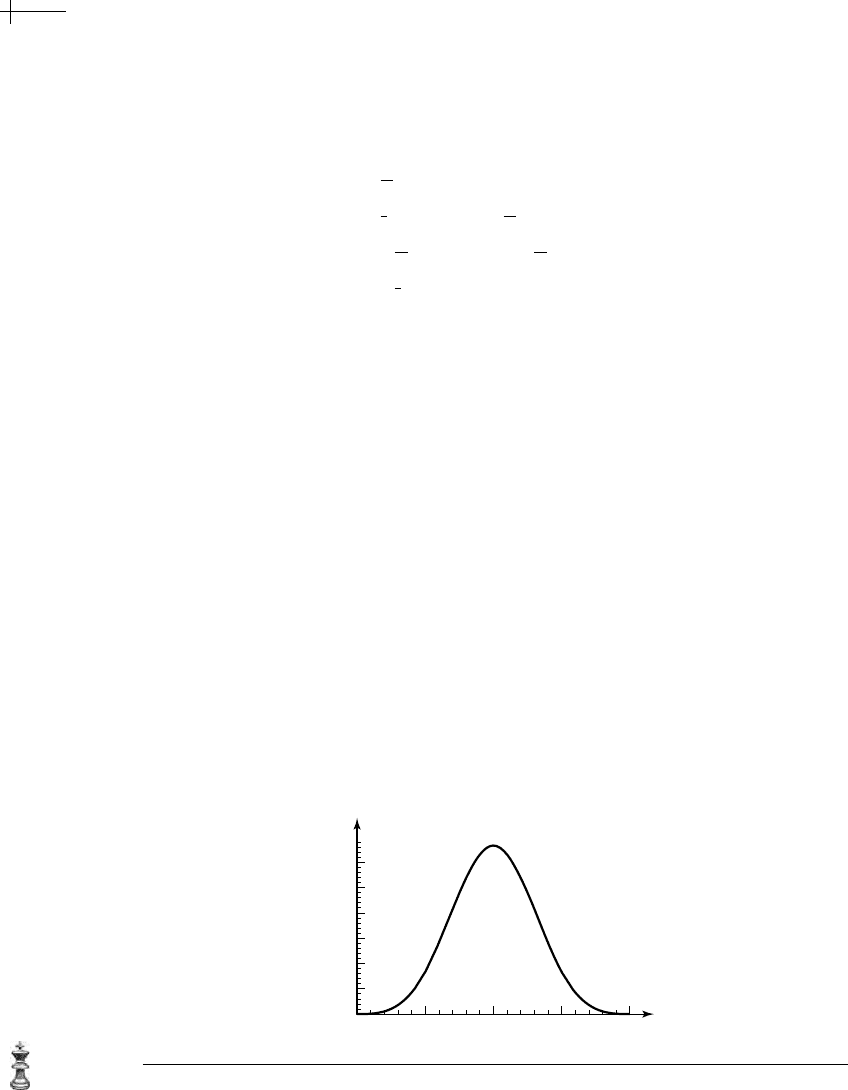
Surprisingly, these seemingly unrelated polynomials define a very nice smooth

bump function, graphed in Figure 1.4. (

n[x] is the cubic B-spline basis function.)

Representing each of these polynomial functions in the monomial basis gives

no clue about the shape of the graph of

n[x]. Ideally, the definition of n[x] as a

piecewise polynomial should provide information about the shape of its graph. The

careful choice of an appropriate basis for the piecewise polynomials provides the

solution to this problem. The coefficients of this basis should give some geometric

information about the shape of the graph of the resulting piecewise polynomial

function. In particular, these coefficients should define a piecewise linear shape

that approximates the associated function. This idea of relating a piecewise linear

shape to an associated continuous shape is one of the fundamental paradigms of

geometric design. As we shall see later, subdivision is one of the most successful

instances of this paradigm.

1234

Figure 1.4 Plot of the piecewise cubic polynomial n[x].

1.1 Functions 5

1.1.2 B´ezier Curves

Perhaps the simplest example of a functional representation that embodies this

paradigm is that of Bernstein polynomials and B

ezier curves. Our goal in this sec-

tion is to give a brief introduction to B

ezier curves in preparation for discussing

subdivision for these curves later in the chapter. For those readers interested in a

more complete exploration of the properties of B

ezier curves, the authors suggest

Farin [59] or Bartels et al. [9].

Recall that our goal is to find a basis whose coefficients provide geometric

intuition concerning the shape of the function defined by these coefficients. To

be specific, let us first consider the problem of representing a single polynomial

function

p[x] of degree m over the unit interval [0, 1]. For polynomials, the key idea

is to construct a set of

m + 1 basis functions b

[x] of degree m where 0 ≤ i ≤ m. Then,

every polynomial

p[x] of degree m can be represented as a unique linear combination

of these basis functions:

p[x] =



i =0

p[[ i ]]b

[x]. (1.1)

Here, the m + 1 coefficients are represented as a column vector p whose i th co-

efficient is denoted by

p[[ i ]]

. For the sake of notational compactness, equation 1.1

can also be in vector form as

p[x] = B

[x]p, where B

[x] is a row vector consisting of

the

m + 1 basis function b

[x].

If the basis functions

[x] are chosen to be the Bernstein basis functions, the

coefficients of

p provide strong geometric intuition about the behavior of p[x] on the

interval

[0, 1]. The Bernstein basis functions can be defined in a variety of manners.

One simple construction is to consider the binomial expansion of the expression

((1 − x) + x)

. The binomial expansion consists of m + 1 terms of degree m in x.For

example,

((1 − x) + x)

== (1 − x)

+ 3(1 − x)

x + 3(1 − x)x

+ x

The resulting terms of this expansion are the Bernstein basis functions of degree m.

Applying the binomial theorem yields an explicit expression for the

i th Bernstein

basis function of degree

[x] =





(1 − x)

m−i

. (1.2)

6 CHAPTER 1 Subdivision: Functions as Fractals

.2 .4 .6

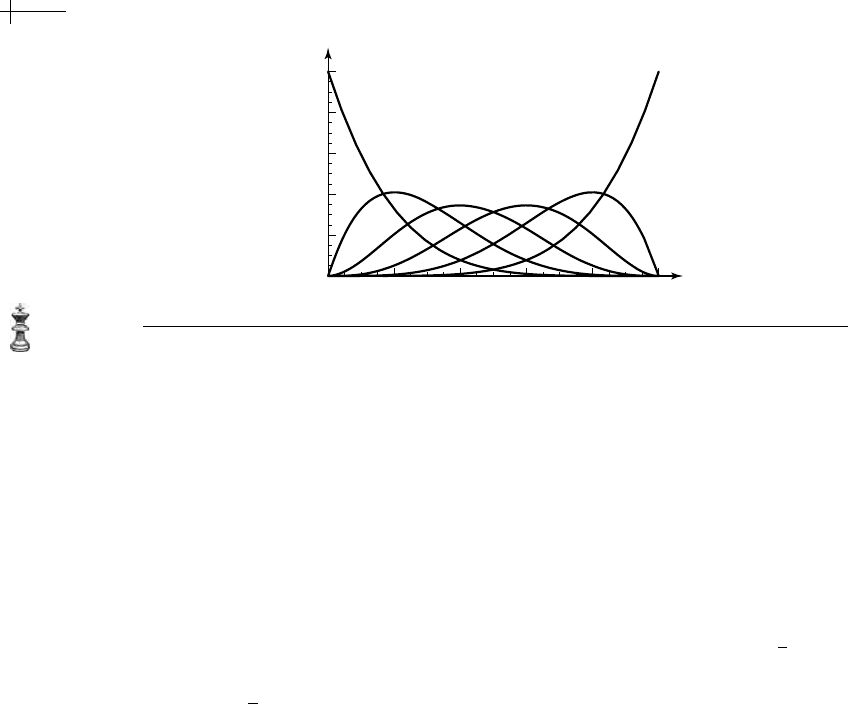
Figure 1.5 Plots of the six quintic Bernstein basis functions b

[x].

Figure 1.5 shows a plot of the six Bernstein basis functions b

[x] of degree five.

These basis functions have a wide range of remarkable properties. These properties

include:

■

The functions b

[x] are non-negative polynomials of degree m on the interval

[0, 1].

■



i =0

[x] == 1 due to the definition of the b

[x] in terms of the binomial

expansion.

■

[x] is a bell-shaped function that reaches its maximum at x ==

. (This

property can be verified by noting that the derivative of

[x] is zero at

x ==

If the entries of the vector

p are points (instead of scalar coefficients), p[x] is a

parametric curve known as a B´ezier curve. The open polygon defined by the

m + 1

control points of p is the control polygon associated with the curve p[x]. Observe

that the definition of equation 1.1 involves only weighted combinations of the

control points of the form



p[[ i ]]. Because the Bernstein basis functions b

[x]

sum to one, these weights α

always sum to one (i.e.,



== 1). Taking such an

affine combination of a set of points is a frequent operation in geometric design;

restricting the sum of the weights to be one guarantees that the sum



p[[ i ]] is a

well-defined point whose location is independent of the particular coordinate sys-

tem used in representing the points

p[[ i ]]. (Technically, the construction is affinely

invariant.)

Due to the properties of the Bernstein polynomials, the B

ezier curve

p[x] follows

the control polygon

p in a very natural manner as x varies from 0 to 1. For example,

1.1 Functions 7

.5 1 1.5 2

1.5

.5 1 1.5 2 2.5 3

1.5

2.5

123456

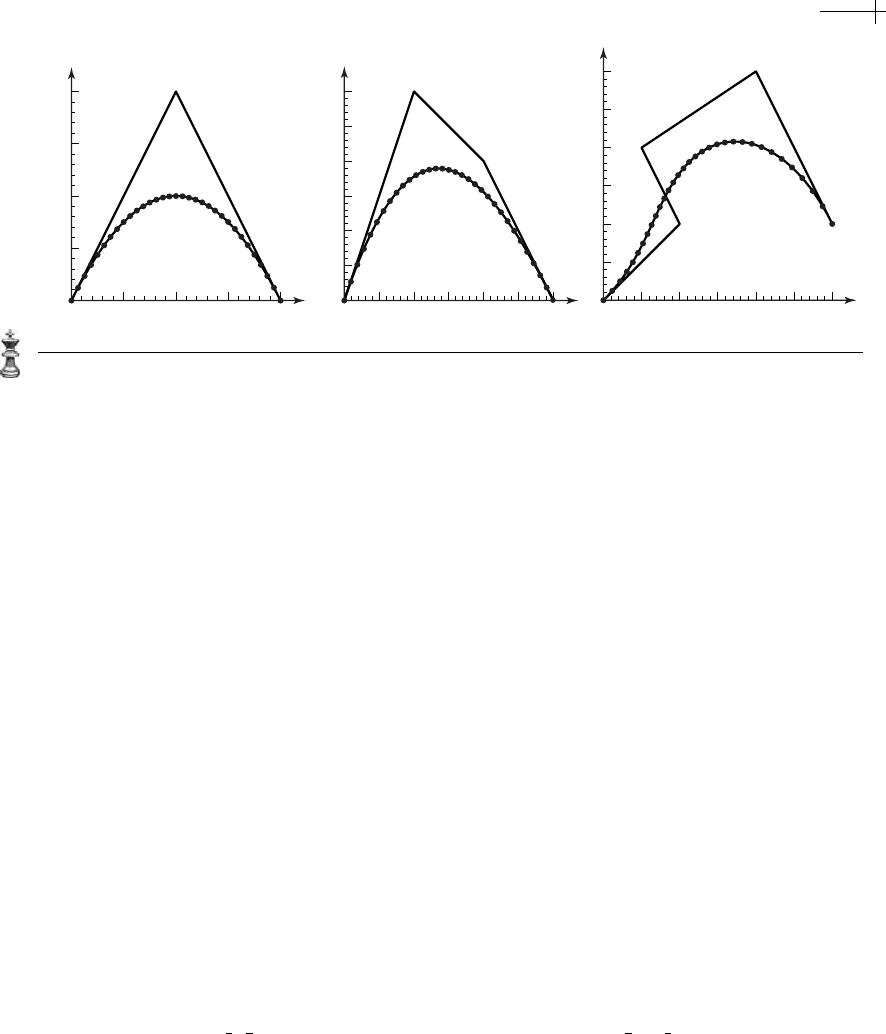
Figure 1.6 Several B ´ezier curves and their control polygons.

p[x]

interpolates the endpoints of the polygon p (i.e., p[0] == p[[0]] and p[1] == p[[m]]).

Because the Bernstein basis functions

[x] are non-negative on the interval [0, 1],

p[x] is an affine combination of the points p[[ i ]], where the weights are always non-

negative. Such a combination is called a convex combination because the resulting

point always lies inside the convex hull of the points

p[[ i ]]. Figure 1.6 shows several

control polygons and their corresponding B

ezier curves

p[x].

This method for defining parametric curves and using them to design shapes

was discovered independently by two researchers for rival French automakers in the

early 1960s. One researcher, P. B

ezier of Renault, was able to publish his ideas; the

resulting curves became known as B

ezier curves. The other researcher, P. de Castel-

jau of Citro

en, was not allowed to publish his ideas, because they were viewed as

trade secrets by Citro

en. It was not until 1972 that the link between these two inde-

pendent pieces of work was uncovered [76]. (Do not feel too sorry for de Casteljau;

the subdivision algorithm for B

ezier curves is known as the de Casteljau algorithm

in honor of his contributions.)

Due to its many nice properties, a designer can control the shape of the B

ezier

curve

p[x] simply by manipulating the polygon p. Ideally, this manipulation of B

ezier

curves should be done interactively. The designer modifies

p and the modeling

system instantly updates

p[x]. To achieve this goal, the system should produce some

type of dense polygonal approximation to

p[x] that can be rendered easily on the

screen. The simplest approach is to evaluate

p[x] at a sequence of n + 1 values

x ={0,

, ..., 1} and to render the polygon {p[0], p[

], p[

], ..., p[1]}.Asn →∞,

this discrete approximation converges to the true B

ezier curve

p[x]. Figure 1.6 uses

such a discretization for

n = 32.

8 CHAPTER 1 Subdivision: Functions as Fractals

The rendering method previously described is reasonable but has some flaws.

Evaluating

p[x] repeatedly to compute {p[0], p[

], p[

], ..., p[1]} is expensive. Much

more efficient methods for repeated evaluation, such as forward differencing [2, 9],

exist. (Note that forward differencing is not always numerically stable.) Another

drawback is the need to determine

n prior to the discretization. If n proves to be

too small (i.e., the discrete approximation does not follow

p[x] closely enough),

p[x] must be reevaluated using a larger n. One simple trick, which avoids this total

recomputation, is to replace

n by 2n. To compute {p[0], p[

], p[

], ..., p[1]}, one need

only compute the value of

p[x] at x =

, ...,

2n−1

. The remaining values have

already been computed earlier. Because this algorithm determines discretizations of

p[x] of increasingly fine resolution, this procedure is an example of a multiresolution

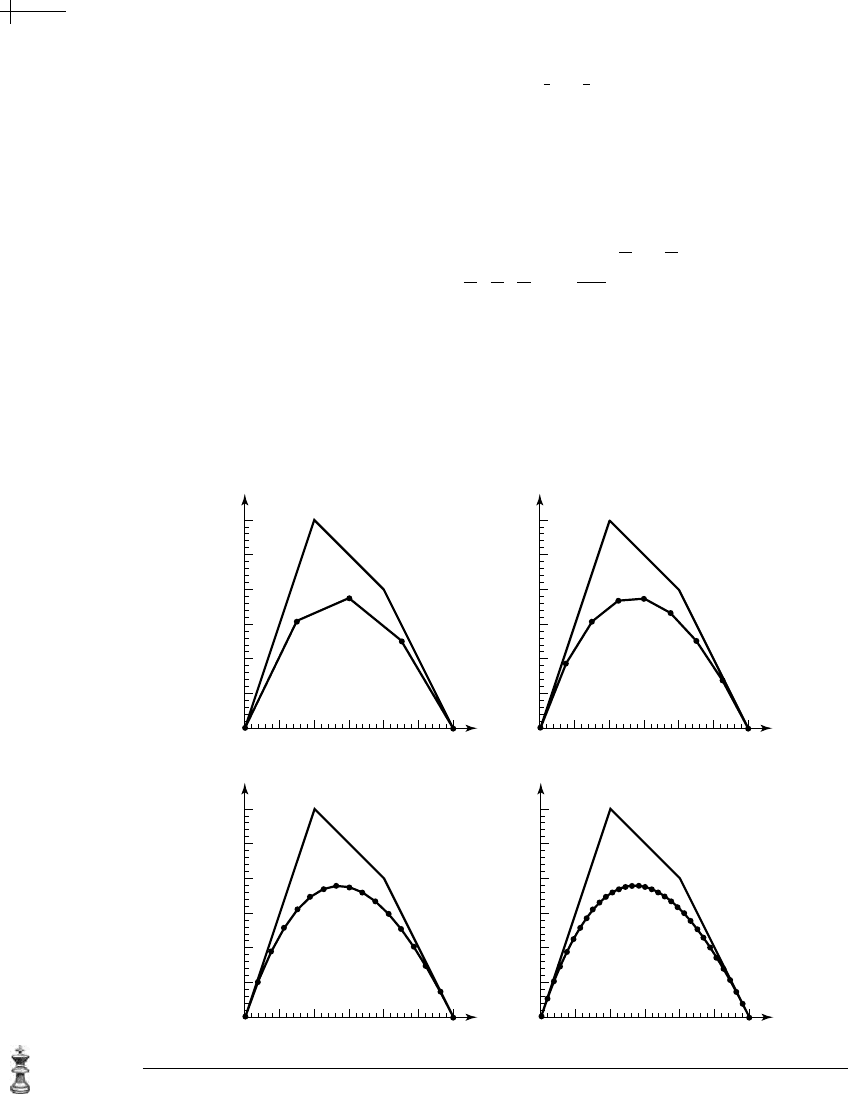
algorithm. Figure 1.7 shows an example of this approach applied to a cubic B

ezier

curve for

n = 4, 8, 16, 32.

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

Figure 1.7 A multiresolution algorithm for drawing a cubic B ´ezier curve.

1.2 Fractals 9

1.2 Fractals

The plotting algorithm described at the end of the previous section has an impor-

tant property: it produces increasingly detailed plots of a function by doubling the

resolution of the plot at each step. Eventually, the plots converge to the exact B

ezier

curve. This method is a simple example of a multiresolution algorithm. Starting

with a coarse shape, multiresolution methods build increasingly ﬁner shapes that

eventually converge to some limit shape. Ideally, successive shapes are related by

a simple transformation. In the case of B

ezier curves, the actual transformation

relating two consecutive approximations is not quite clear. As described in the pre-

vious section, each approximation was actually computed directly from the coarsest

starting shape. The true multiresolution nature of B

ezier curves will become clearer

later in this section.

This section considers another interesting example of multiresolution shapes:

fractals. Conceptually, building a fractal requires two ingredients: a space of geo-

metric shapes

and a transformation S that maps a coarse shape p

k−1

to a fine

shape

. Given an initial shape p

, a fractal method defines an infinite sequence

of shapes by iterating

S according to p

= Sp

k−1

. (The expression Sp

k−1

denotes

the application of

S to p

k−1

.) If the transformation S is chosen appropriately, the

limit of

as k →∞is a well-defined shape p

∞

satisfying the fixed-point prop-

erty

∞

= Sp

∞

. Most of the material on constructing fractals using this approach is

drawn from Barnsley [8], an excellent introduction to the area of fractals.

1.2.1 Iterated Afﬁne Transformations

One of the simplest methods for constructing fractals involves iterating a set of

affine transformations. Before attempting to construct fractals using this method,

we briefly review some of the properties of affine transformations and discuss an

elegant method for representing affine transformations. Mathematically, an affine

transformation is a function

A that maps points to points and satisfies the relation





p[[ i ]]





A[p[[i]]] (1.3)

for all vectors of points p provided that



== 1. For points in the plane, some

standard examples of affine transformations include rigid-body motions, such as

rotations and translations, as well as scaling and shearing. (See Mortenson [108] for

more information on affine transformations.)

10 CHAPTER 1 Subdivision: Functions as Fractals

One interesting feature of affine transformations in the plane is that once the

value of an affine transformation

A is known at three noncollinear points p[[0]], p[[1]]

and p[[2]] the action of A on an arbitrary point v can be computed using equation 1.3.

The trick is to express the point

v as an affine combination of the points p[[0]], p[[1]],

and

p[[2]]; that is, v == α

p[[0]] +α

p[[1]] +α

p[[2]], where α

+α

== 1. Given these

weights

, the value A [v] of the affine transformation

A satisfies

A [v] = α

A [p[[0]]] + α

A [p[[1]]] + α

A [p[[2]]]

due to equation 1.3. These affine weights are the barycentric coordinates of v with

respect to the base triangle

p and can be computed as the ratio of the areas of

various triangles defined by

v and the vertices of p,

{α

, α

{area[v, p[[1]], p[[2]]], area[p[[0]], v, p[[2]]], area[p[[0]], p[[1]] , v]}

area[p[[0]], p[[1]], p[[2]]]

(1.4)

Given this observation, all that remains is to specify the behavior of A at the vertices

p. One simple solution is to express the position of points A[p[[i]]] in terms of

their barycentric coordinates with respect to the triangle

p. These three sets of

coordinates can be collected into a

3 × 3 matrix S whose rows are the barycentric

coordinates for

A [p[[0]]], A [p[[1]]], and A [p[[2]]] with respect to the triangle p. Given a

point

v with barycentric coordinates {α

, α

} with respect to the triangle p, the

barycentric coordinates of

A [v] with respect to points A [p[[0]]], A [ p[[1]]], and A [p[[2]]]

are the vector/matrix product {α

, α

}S.

To illustrate this method, we next construct the matrix

S that represents the

affine transformation mapping a base triangle

p to an image triangle q. These two

triangles themselves are represented as a column vector consisting of three points in

the plane; that is, a

3×2 matrix, where each row contains the Cartesian coordinates

of the vertices of the triangle. For our example, we let

p and q be the triangles

p =

⎛

⎜

⎝

⎞

⎟

⎠

, q =

⎛

⎜

⎝

⎞

⎟

⎠

As observed, the rows of the matrix S are the barycentric coordinates of the vertices

q with respect to the base triangle p. Because q[[0]] == p[[0]], the first row of S

is simply {1, 0, 0}. Similarly, q[[1]] is the midpoint of the edge from p[[0]] to p[[1]].

Therefore, the second row of

S is {

, 0}. Finally, q[[2]] is the midpoint of the edge

1.2 Fractals 11

from p[[0]] to p[[2]]. Therefore, the third and final row of S is {

, 0,

}. Thus, the

matrix

S has the form

S =

⎛

⎜

⎝

100

⎞

⎟

⎠

Observe that the matrix S satisfies q = Sp. One quick way to compute S from

p and q is as follows: extend both p and q to form 3 × 3 matrices, p and q,by

adding an extra column of

1s (i.e., converting the coordinates of p and q to their

homogeneous form). Because the rows of

S sum to one, these extended matrices

satisfy

Sp = q. As long as p is a nondegenerate triangle, the matrix p is invertible

and

S is exactly qp

−1

. In terms of our previous example,

⎛

⎜

⎝

100

⎞

⎟

⎠

⎛

⎜

⎝

001

101

⎞

⎟

⎠

⎛

⎜

⎝

001

201

111

⎞

⎟

⎠

−1

Observe that the matrix S actually encodes a relative transformation with re-

spect to the base triangle

p. Choosing a different base triangle defines a different

transformation. This particular method of representing affine transformations is

advantageous in that many of the constructions for fractals have the form “Take a

shape

p and transform it as follows.” The matrix S encapsulates this relative trans-

formation without encoding any particular information about the base triangle

For example, the action of the matrix

S shown previously is to shrink the triangle p

by a factor of

and reposition the image triangle q so that it continues to touch the

first vertex of

p. Figure 1.8 shows the result of applying the affine transformation

associated with

S to two different base triangles p (outlined). The corresponding

triangles

q = Sp are black.

Figure 1.8 Application of the transformation S to the large outlined triangles yields the smaller solid

triangles.

12 CHAPTER 1 Subdivision: Functions as Fractals

Given an affine transformation encoded by a matrix S, we can now consider

the question of iterating this transformation via

= Sp

k−1

. In particular, if p

some base triangle, we are interested in the behavior of the triangles

as k →∞.

To answer this question, we note that an affine transformation

A is contractive if

there exists a constant

0 ≤ β<1 such that

dist [A [u], A [v]] ≤ β ∗dist [u, v]

for all points u, v in the plane. (dist [u, v] is the Euclidean distance between the points

u and v.) If the affine transformation associated with S is contractive, the diameter

of the triangles

decreases after each application of S and therefore the limit of

this process is a point.

Of course, fractals consisting of a single point are not particularly interesting.

However, if we consider a set of contractive affine transformations, iterating the

composite transformation consisting of the union of these transformations yields a

much more interesting limit shape. If

S is a set of matrices associated with these

affine transformations and

p is a set of triangles, we let Sp denote the new set of

triangles representing all possible combinations of applying any one transformation

from

S to one triangle from p. Obviously, the size of the resulting set is the product

of the size of the set of transformations and the size of the set of input triangles.

In this framework, we can now define the fractal process, mapping sets of triangles

k−1

to sets of triangles p

,as

= Sp

k−1

If each of the affine transformations in S is contractive, the limit of this process is a

fixed set of points

∞

whose shape depends on S and the base triangle p

. Instead

of attempting to characterize and prove this convergence, we refer the interested

reader to Chapters 2 and 3 of Barnsley [8]. Our agenda for the remainder of this

section is to consider some intriguing examples of this fractal process and to show

that the B

ezier curves introduced in section 1.1 can be represented as the limit of

this process.

1.2.2 The Sierpinski Triangle

Our first example of a fractal process is the Sierpinski triangle. Conceptually, the set

of iterated affine transformations describing the fractal process for the Sierpinski

1.2 Fractals 13

Figure 1.9 Progressive approximations to the Sierpinski triangle.

triangle maps a base triangle into three children by splitting each edge of the base

triangle in half. The set

S of transformations consists of the three matrices

S =

⎧

⎪

⎨

⎪

⎩

⎛

⎜

⎝

100

⎞

⎟

⎠

⎛

⎜

⎝

010

⎞

⎟

⎠

⎛

⎜

⎝

001

⎞

⎟

⎠

⎫

⎪

⎬

⎪

⎭

Because each of these transformations is contractive (with β ==

), there exists a

fractal, the Sierpinski triangle, associated with the limit of the iteration

= Sp

k−1

To draw the Sierpinski fractal, we repeatedly apply the set of affine transformations

S to a single base triangle p

until the size of the triangles in the set p

falls below

the desired resolution. Figure 1.9 shows the result of applying this process five

times to the gray base triangle

Based on the figure, we observe that the Sierpinski triangle has a very curious

property: the final shape consists of three copies of itself, placed in the three corners

of the original triangle. In fact, the three shapes are exactly the result of applying the

three affine transformations from

S to the Sierpinski triangle itself. This property

follows from the fact that the limit shape

∞

is a fixed point of the transforma-

tion

S (i.e., p

∞

= Sp

∞

). This self-similarity relation (often referred to as the collage

property) is characteristic of fractals defined by iterated affine transformations.

1.2.3 The Koch Snowﬂake

A second example of this fractal process is the Koch snowflake. Here, the set of

affine transformations

S has the form

S =

⎧

⎪

⎨

⎪

⎩

⎛

⎜

⎝

100

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

001

⎞

⎟

⎠

⎫

⎪

⎬

⎪

⎭