Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

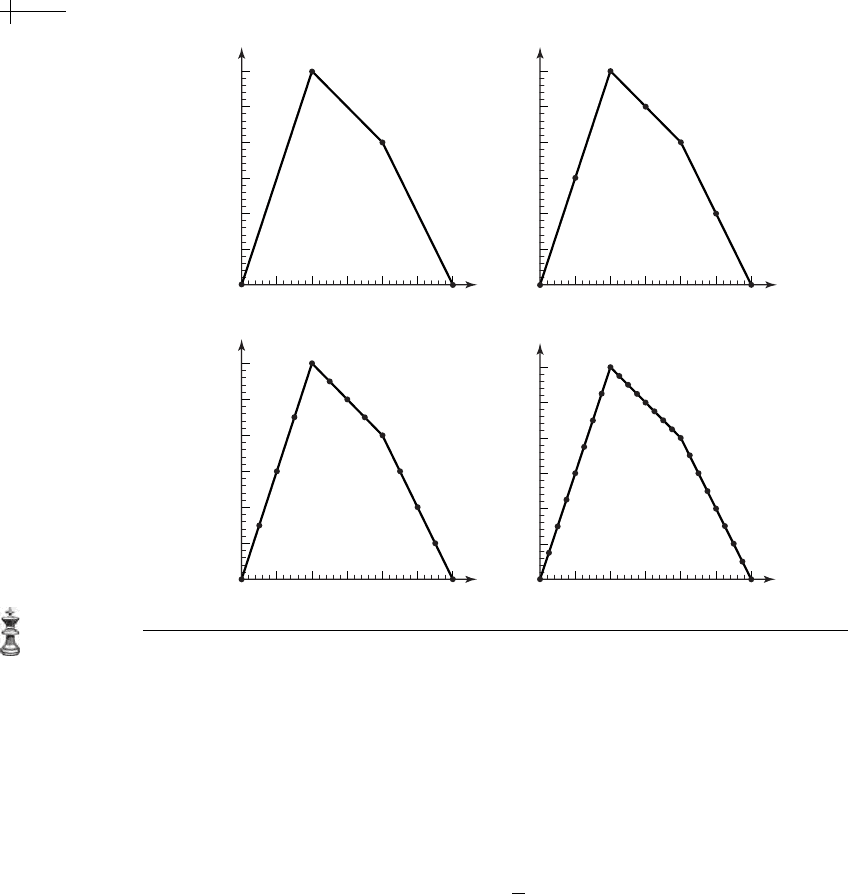
24 CHAPTER 1 Subdivision: Functions as Fractals

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

.5 1 1.5 2 2.5 3

1.5

2.5

Figure 1.21 Progression of the subdivision process for a piecewise linear function.

approximation to shape of the function p[x]. Figure 1.21 shows three rounds of this

refinement procedure starting from

⎛

⎜

⎝

⎞

⎟

⎠

The i th coefficient of p

is plotted at x ==

This process of taking a coarse approximation

and computing increasingly

dense approximations

to a final limit function p[x ] is referred to as subdivision.

The beauty of subdivision is that we can now ignore the functions

N [2

x] entirely,

and instead rely on the subdivision matrix

S when generating approximations to p[x].

In effect, subdivision is a multiresolution rendering algorithm that generates increas-

ingly dense plots by taking convex combinations of points used in previous plots.

Note that these convex combinations, embodied by

k−1

, can be computed

without constructing the entire subdivision matrix

S. Because the columns of S are

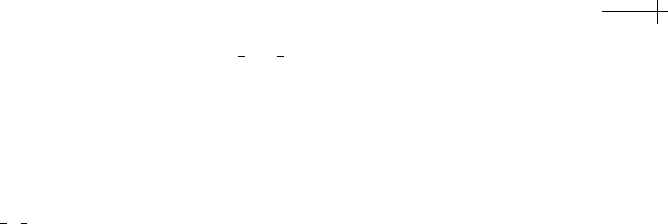
1.4 Overview 25

two-shifts of the sequence {..., 0,

, 1,

, 0, ...}, multiplication of the matrix S by

a column vector of coefficients

k−1

determines new coefficients in the vector p

according to two simple rules. Coeff icients in even-indexed rows of p

correspond

to coefficients from

k−1

, because the weights in the even-indexed rows of S are

{..., 0, 1, 0, ...}. Coefficients in odd-indexed rows of p

are the average of two con-

secutive coefficients from

k−1

, because the odd-indexed rows of S

have the form

{..., 0,

, 0, ...}.

As seen from this example, subdivision is potentially a very powerful method

of modeling shapes. In particular, it combines the best of functional and frac-

tal representations. As this book will demonstrate, subdivision has four principal

advantages:

■

Ease of use: Modeling with subdivision is easy to implement because it

involves only discrete shapes.

■

Expressiveness: Simple subdivision schemes can reproduce a large class of

interesting shapes.

■

Efficiency: Many subdivision schemes use repeated averaging, a fast method

of computing discrete approximations of the limit shapes.

■

Linear analysis tools: The subdivision process defines scaling functions

whose properties can be analyzed using linear algebra.

1.4 Overview

One interesting property of the subdivision scheme for linear splines is that it makes

no explicit use of the piecewise polynomial definition of the unit hat function

n[x].

The scheme used only the subdivision matrix

S. For piecewise linear splines, the

subdivision matrix

S was “nice” (i.e., it defined a convergent process). Thus, the

scaling functions

N [2

x] associated with the subdivision scheme could be computed

entirely in terms of the matrix

S. To recover a scaling function in N [x], one would

simply apply the subdivision process to the vector

{..., 0, 0, 1, 0, 0, ...}. This obser-

vation allows us to focus our entire attention on the subdivision matrix

S and leads

to two related questions:

■

How can we construct a subdivision matrix S whose associated limit func-

tions are “interesting”?

■

Given a subdivision matrix S, is the associated subdivision scheme conver-

gent? If so, are the associated limit functions smooth?

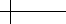
26 CHAPTER 1 Subdivision: Functions as Fractals

The next two chapters of this book address these two questions. Chapter 2

introduces a simple technique for generating subdivision schemes: directional in-

tegration. This integral approach is the standard technique used in constructing

subdivision schemes for B-splines and box splines and leads directly to a simple

repeated averaging algorithm for subdividing these splines. Chapter 3 considers the

second question of convergence and smoothness. The key to answering this ques-

tion is developing a method for subdividing various differences associated with the

vector

. Taken together, the first three chapters of this book form an introduction

to the basics of subdivision.

The second part of the book (Chapters 4, 5, and 6) reconsiders the first prob-

lem in more detail. Chapter 4 introduces an alternative approach, developed by

the authors, for constructing “interesting” subdivision schemes. This differential

method, although slightly more complicated, is capable of generating a wider range

of schemes than those produced by the integral method. For example, the last

section in Chapter 4 introduces a new curve subdivision scheme that reproduces

splines in tension, B-splines, and trigonometric splines as special cases of a more

general scheme. This subdivision scheme is the building block for a new scheme for

surfaces of revolution introduced in Chapter 7. As an application of the differential

method, Chapter 5 derives an infinitely supported subdivision scheme for solu-

tions to the harmonic equation via the differential approach and discusses building

finite approximations to this scheme. Chapter 6 considers variational extensions of

the differential method for the problem of generating subdivision rules along the

boundaries of finite domains.

The last part of the book, Chapters 7 and 8, introduces and analyzes a range of

subdivision schemes for polyhedral meshes. Chapter 7 discusses an elegant method

of subdividing surface meshes using repeated averaging (including an extension to

the case of surfaces of revolution). This chapter also includes a simple method

for handling creases and boundaries of subdivision surfaces. Chapter 8 extends the

smoothness tests developed in Chapter 3 to the extraordinary vertices of these

surface schemes and concludes by considering some of the promising areas for

future research on subdivision.

CHAPTER 2

An Integral Approach to

Uniform Subdivision

Chapter 1 provided a glimpse into the nature of subdivision. The key to building

a subdivision scheme for splines with uniformly spaced knots is a scaling func-

tion

n[x] that possesses a refinement relation, that is, an expression of the function

n[x] as a linear combination of integer translates of its dilates, n[2x − i]. For ex-

ample, the scaling function for piecewise linear splines satisfies the refinement

relation

n[x] ==

n[2x + 1] + n[2x] +

n[2x − 1].

(2.1)

The coefficients s of this refinement relation are then used to define a two-slanted

matrix

S that relates coefficient vectors p

k−1

and p

defined on the grids

k−1

Z and

Z, respectively, via the subdivision relation p

= Sp

k−1

This chapter introduces a general method for creating scaling functions that

may be refined: directional integration. For example, the B-spline basis functions

have a simple recursive definition in terms of integration. Based on this definition,

we derive the refinement relation for B-splines and construct the associated subdi-

vision scheme. Later in the chapter, we describe an equivalent geometric method

for constructing the B-spline basis functions as the cross-sectional volumes of high-

dimensional hypercubes. This construction easily generalizes from the univariate

case to the bivariate case and allows creation of refineable scaling functions in two

variables. The splines associated with these scaling functions, box splines, also have

an elegant subdivision algorithm. The chapter concludes with a simple method for

constructing explicit piecewise polynomial expressions for both B-splines and box

splines. Again, these constructions have an interesting geometric interpretation in

terms of high-dimensional geometry.

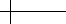
28 CHAPTER 2 An Integral Approach to Uniform Subdivision

2.1 A Subdivision Scheme for B-splines

Chapter 1 introduced a simple method for constructing a smooth curve that fol-

lowed a control polygon

p with m + 1 vertices. The B

ezier curve p[x] associated

with

p is a parametric curve of degree m that approximates p as x varies from 0

to 1. For small values of m, the B

ezier technique works well. However, as m grows

large (say,

m > 20), B

ezier curves begin to exhibit some undesirable properties. In

particular, the Bernstein basis functions

[x] are supported over the entire interval

[0, 1]. Therefore, modifying any one of the control points in p induces a change to

the entire curve

p[x]. Moreover, subdividing p[x] using the de Casteljau algorithm

requires

O[m

] computations.

One solution to this problem is to construct a collection of B

ezier curves, say

of degree three, that approximate the shape of

p. The resulting composite curve is

a piecewise polynomial curve. This modification allows local control of the com-

posite curve in the sense that modifying one B

ezier curve in the collection does

not necessarily induce a change in the entire curve. Moreover, subdividing the

O[m]

ezier curves of degree three can be done in O[m] time. Because in many applica-

tions it is desirable for this composite curve to be smooth (i.e., have a continuous

derivative), any method for representing

p[x] as a collection of B

ezier curves must

ensure that the control polygons for consecutive B

ezier curves meet smoothly.

An alternative approach is to construct a set of smooth piecewise polyno-

mial basis functions that behave like the Bernstein basis functions. Instead of being

globally supported, each basis function is locally supported. For example, if the

associated curve

p[x] is defined on the interval [0, m], the i th basis function is sup-

ported only over a small subrange, say

[i − 2, i + 2] for cubic splines. Taking linear

combinations of these smooth basis functions automatically yields a smooth curve

p[x]. The advantage of this approach is that there is no need to manage each poly-

nomial piece of

p[x] explicitly; smoothness of the entire curve p[x] is guaranteed by

construction.

The canonical example of such smooth piecewise polynomial basis functions

is the B-spline basis functions. If the breakpoints between each polynomial piece

(i.e., the knots) are placed at the integers, the curve formed by taking linear com-

binations of these basis functions is a uniform B-spline. Uniform B-splines are a

fundamental tool in a number of areas, including numerical analysis, finite element

methods, geometric design, and computer graphics. The success story of B-splines

in geometric design starts with the landmark publications by De Boor [37, 38].

Bartels et al. [9] give an extensive introduction to the various remarkable proper-

ties and algorithms associated with B-splines.

2.1 A Subdivision Scheme for B-splines 29

2.1.1 B-spline Basis Functions via Repeated Integration

We begin our discussion of B-splines with a definition of B-spline basis functions in

terms of repeated integration. Later, we derive the refinement relation for B-spline

basis functions and conclude by constructing the corresponding subdivision scheme

for uniform B-splines via Lane and Riesenfeld [93]. This subdivision scheme has a

particularly beautiful interpretation in terms of repeated averaging. This averaging

algorithm is simple to implement and provides the intellectual stepping-stone to

the surface schemes discussed in Chapter 7. One important fact the reader should

keep in mind during the rest of this chapter is that although the mathematics

of constructing subdivision schemes may seem complicated the resulting schemes

themselves are beautifully simple.

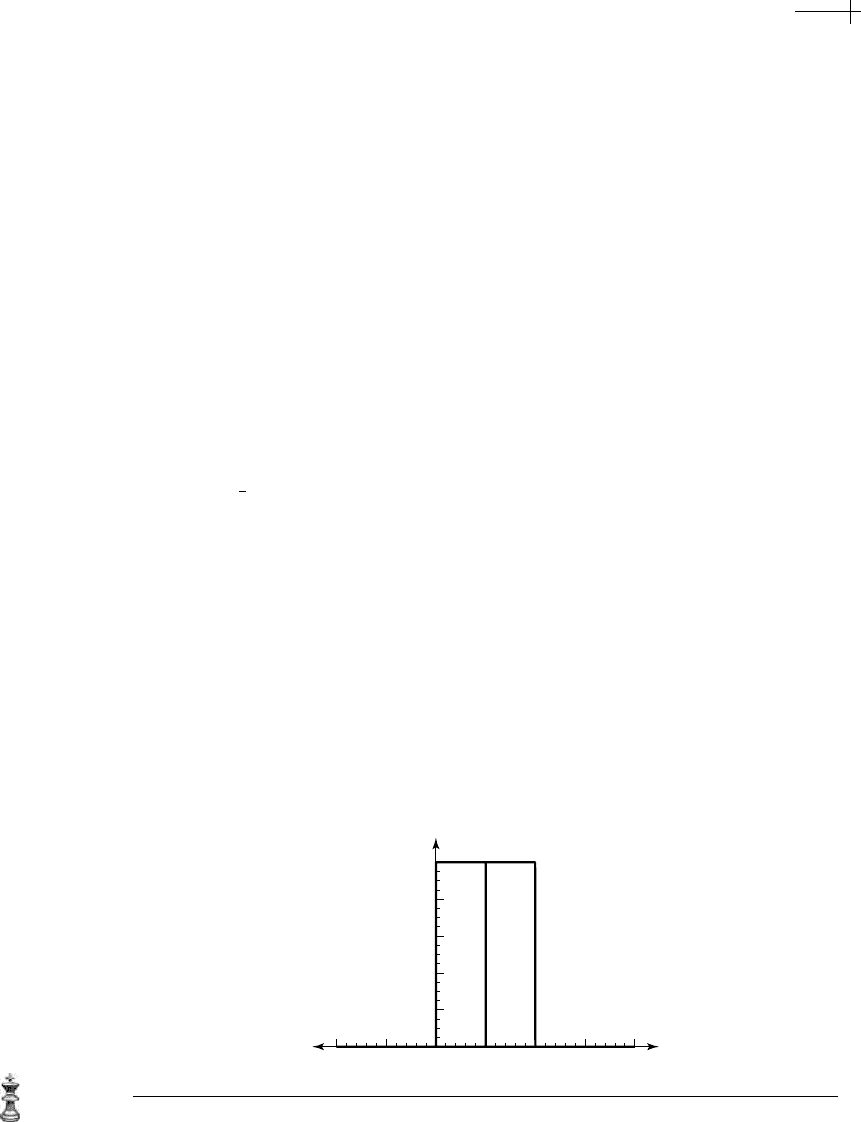
Our definition of B-spline basis functions is recursive. For the base case, the

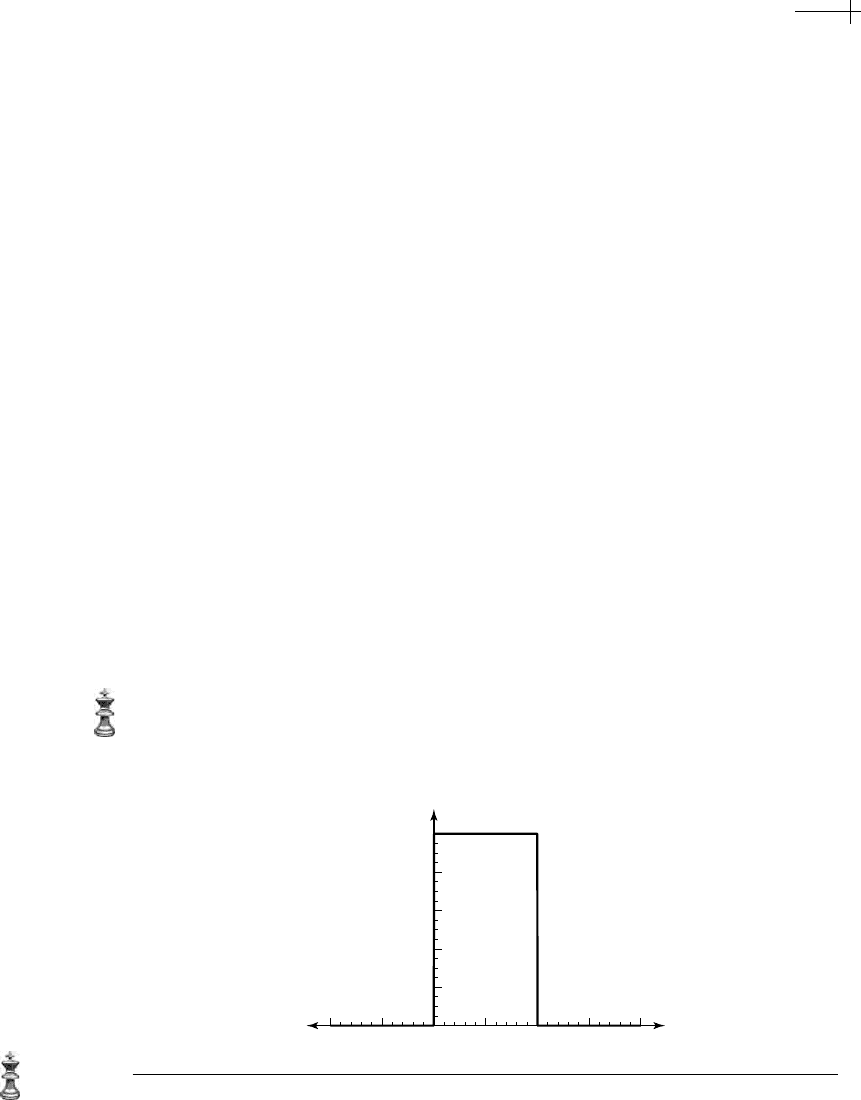
B-spline basis function of order one has the form

[x] =



1 if 0 ≤ x < 1,

0 otherwise.

(2.2)

Figure 2.1 shows the graph of n

[x]. This function is a piecewise constant function

that is zero everywhere except on the interval

[0, 1), where it is the constant one.

(In signal processing circles, this function is also referred to as the Haar scaling

function.) Given the B-spline basis function

m−1

[x], the B-spline basis function of

order

m, n

[x], is defined via the recurrence

[x] =



m−1

[x − t] dt. (2.3)

1 .5 .5 1 1.5 2

Figure 2.1 The B-spline basis function of order one.

30 CHAPTER 2 An Integral Approach to Uniform Subdivision

Note that the order of a B-spline is by construction always one more than the

degree of the B-spline. Due to their definition by repeated integration, B-spline

basis functions have the following easily proven properties:

■

[x] is a C

m−2

piecewise polynomial of degree m − 1, with knots at the inte-

gers

Z. This observation follows from the fact that each round of integration

via equation 2.3 increases the smoothness of a function.

■

[x] is non-negative and is supported on the interval [0, m]. Again, this

observation follows from the inductive definition of

[x].

■

[x] has unit integral. In fact, the sum



i ∈Z

[x −i] is exactly one. This fact

holds trivially for the base case

[x] and follows by induction on m.

Together, these three properties are sufficient to establish that the function

[x]

is unique. Let’s continue by considering some examples of B-spline basis functions

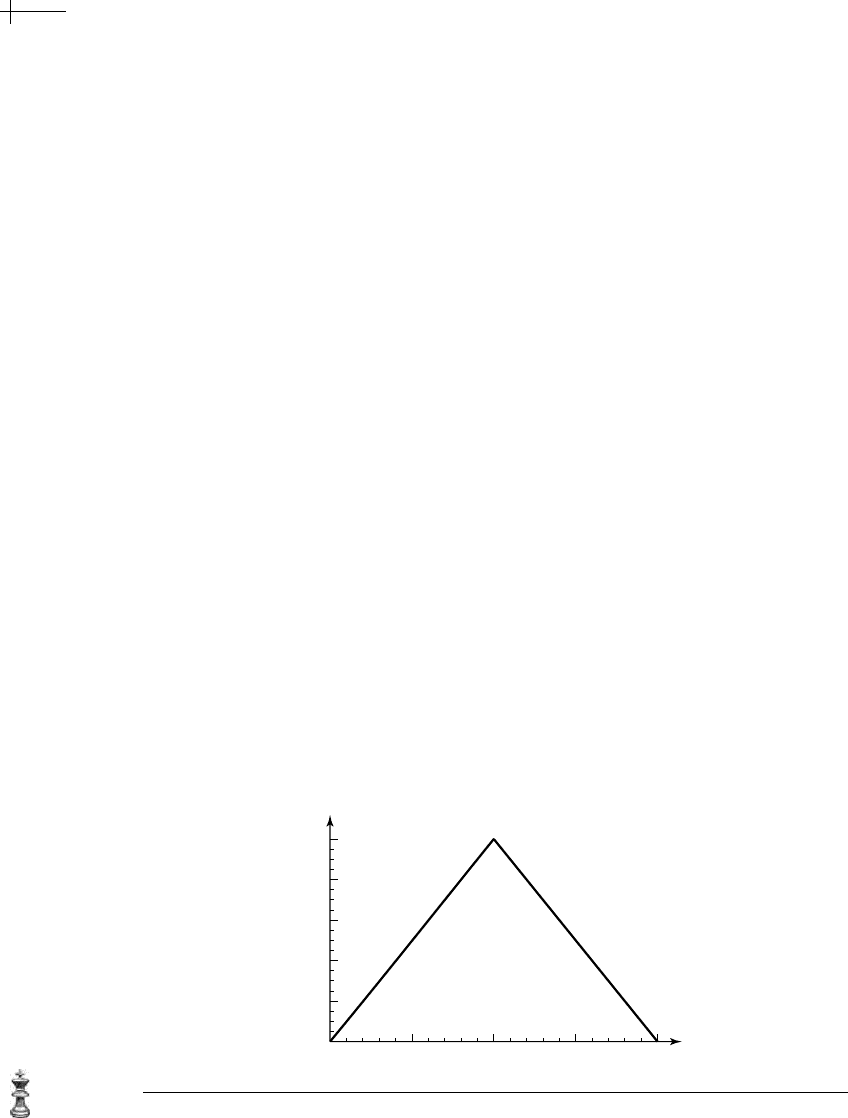
of low order. For example, the B-spline basis function

[x] is a piecewise linear

function of the form

[x] =

⎧

⎨

⎩

x if 0 < x ≤ 1,

2 − x if 1 < x ≤ 2,

0 otherwise.

Figure 2.2 shows a plot of the piecewise linear basis function n

[x]. Due to the

recursive nature of the definition in equation 2.3, this hat function is supported on

the interval

[0, 2] (as opposed to the hat function centered around the origin used

.5 1 1.5 2

Figure 2.2 The linear B-spline basis function (order two).

2.1 A Subdivision Scheme for B-splines 31

.5 1 1.5 2 2.5 3

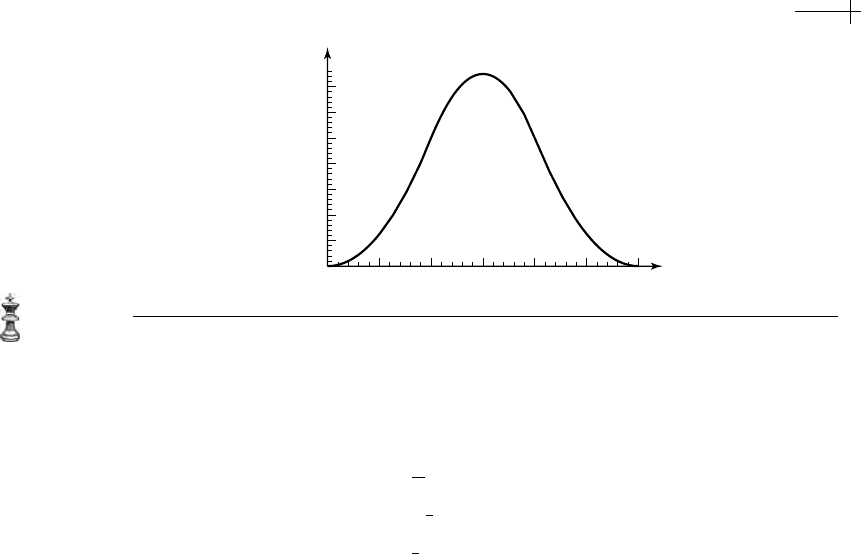
Figure 2.3 The quadratic B-spline basis function (order three).

in Chapter 1). Applying the recursive definition once again yields the piecewise

quadratic basis function

[x] (depicted in Figure 2.3):

[x] =

⎧

⎪

⎨

⎪

⎩

if 0 < x ≤ 1,

−

+ 3x − x

if 1 < x ≤ 2,

(−3 + x)

if 2 < x ≤ 3,

0 otherwise.

An alternative method of defining the B-spline basis function n

[x] involves

repeated convolution with the basis function

[x]. The continuous convolution of

two functions

p[x] and q[x]

, denoted p[x] ⊗q[x], is the integral



∞

−∞

p[t]q[x −t]

dt. (Ob-

serve that the value of this integral is again a function of

x.) Given this definition,

the continuous convolution of the basis functions

[x] and n

m−1

[x] is the integral



∞

−∞

[t]n

m−1

[x − t] dt. Because the effect of multiplying by the function n

[t] inside

this integral is to simply restrict the range of integration for the variable

t to the

interval

[0, 1], this integral reduces to the right-hand side of equation 2.3. Therefore,

the basis function

[x] is simply the continuous convolution of two lower-order

basis functions,

[x] and n

m−1

[x]; that is,

[x] == n

[x] ⊗ n

m−1

[x].

Linear combinations of integer translates of the basis function n

[x] can now be

used to construct arbitrary B-splines. For example, a piecewise constant B-spline

with knots at the integers

Z can be written as a combination of translates of n

[x]:

p[x] =



i ∈Z

p[[ i ]] n

[x − i].

32 CHAPTER 2 An Integral Approach to Uniform Subdivision

1123

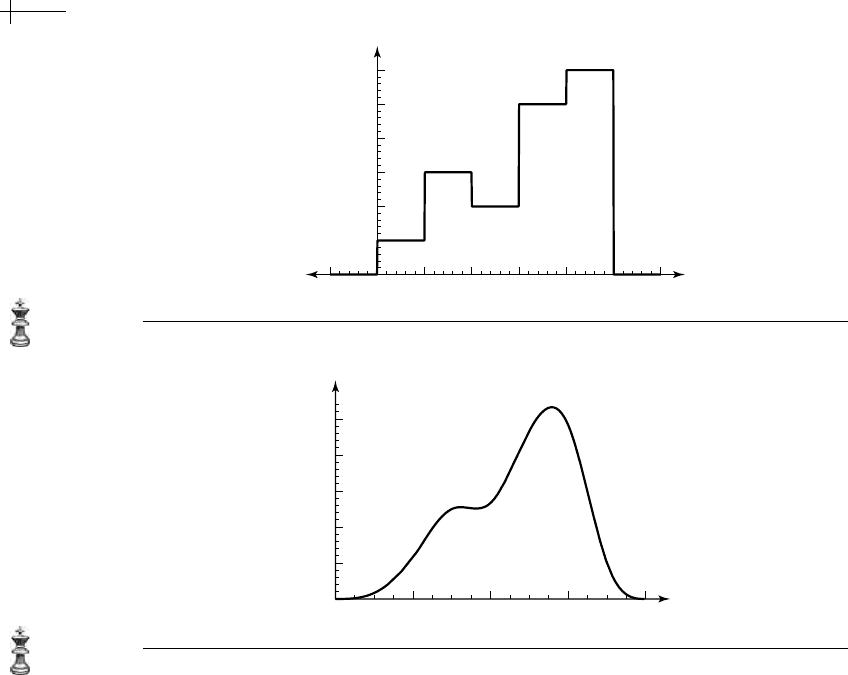
Figure 2.4 A piecewise constant B-spline.

2468

Figure 2.5 A piecewise cubic B-spline.

As in Chapter 1, this expression can be written in vector form as p[x] = N

[x]p,

where

[x] is the vector whose i th entry is n

[x − i]. Figure 2.4 shows a plot of

a piecewise constant B-spline for which the vector

p has the form {..., 0, 1, 3, 2, 5,

6, 0, ...}

. (The non-zero entries of p have indices ranging from 0 to 4.)

Higher-order B-splines

p[x] can be constructed by taking linear combinations

of integer translates of higher-order basis functions (i.e., functions of the form



i ∈Z

p[[ i ]] n

[x −i]). Figure 2.5 shows a cubic B-spline with the same coefficients as

in Figure 2.4. Observe that this function is supported now over the interval

[0, 8],

because the basis function

[x] is supported on the interval [0, 4].

2.1.2 A Reﬁnement Relation for B-spline Basis Functions

For the piecewise linear splines of Chapter 1, the key ingredient in constructing

a subdivision scheme was deriving a refinement relation for the associated scaling

2.1 A Subdivision Scheme for B-splines 33

function. In this section, we derive a refinement relation for the B-spline basis

function of order

m. In general, this relation has the form

[x] ==



i ∈Z

[[ i ]] n

[2x − i]. (2.4)

For uniform schemes, the coefficient sequence s

(m is a superscript here, not an

exponent) is the subdivision mask associated with the refinement relation. Due to

the recursive definition of

[x], the construction for the mask s

is also recursive.

For the base case, we observe that

[x] possesses the particularly simple refinement

relation

[x] == n

[2x] + n

[2x − 1]. (2.5)

The refinement relation of equation 2.5 expresses a basis function defined on a

coarse integer grid

Z as the sum of two basis functions defined on a finer, half-

integer grid

Z. This relation is depicted in Figure 2.6.

A very useful technique for manipulating the subdivision mask

s associated

with a refinement relation is to construct the generating function

s[x ] associated with

the mask

s. By definition, s[x] is the sum of terms of the form s[[i]]x

where i ∈ Z

(i.e., s[x ] =



s[[i]]x

). Be aware that the generating function s[x ] may possess neg-

ative powers of

x and thus is not necessarily a polynomial in x. Returning to

our initial example, the refinement coefficients for

[x] define the subdivision

mask

[x] = 1 + x. (We use the term mask to refer to s and its associated gen-

erating function

s[x ] interchangeably.) For a B-spline basis function of order m,

the subdivision mask

[x] obeys the recurrence relation of Theorem 2.1, which

follows.

1 .5 .5 1 1.5 2

Figure 2.6 The B-spline basis function of order one as the sum of two translates of its dilates.