Волков В.Л. Моделирование процессов и систем в приборостроении

Подождите немного. Документ загружается.

Арзамас 2008

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Нижегородский государственный технический университет им. Р.Е.Алексеева

Арзамасский политехнический институт (филиал НГТУ)

Ассоциация ученых города Арзамаса

В.Л. Волков

МОДЕЛИРОВАНИЕ

ПРОЦЕССОВ И СИСТЕМ

В ПРИБОРОСТРОЕНИИ

Учебное пособие

ля студентов технических специальностей

дневной, вечерней, и заочной форм обучения

СИСТЕМА

МОДЕЛЬ

ЭКСПЕРИМЕНТ

УДК: 681.5.01:621.317.08 (075.8)

Волков В.Л. Моделирование процессов и систем в приборостроении.

Учебное пособие для студентов технических специальностей дневной, вечер-

ней и заочной форм обучения / Арзамас, АПИ НГТУ, 2008. − 143 с.

ISBN 5-230-03038-0.

В учебном пособии представлены сведения по математическому моделированию

динамических систем и процессов в приборостроении. Особенности задач моделирова-

ния в приборостроении заключаются в применении универсального математического

аппарата в виде дифференциальных уравнений, матричных преобразований и стохасти-

ческих процессов.

Классические математические модели рассмотрены в предыдущем издании учеб-

ного пособия [1]. Здесь представлены современные вопросы моделирования, основан-

ные на применении современного векторно-матричного математического аппарата, и

рассмотрены практические задачи моделирования на компьютерах с применением ли-

цензионного объектно-ориентированного программного обеспечения.

Печатается по решению кафедры “Авиационные приборы и устройства”

Арзамасского политехнического института (филиала) НГТУ.

Рецензент - канд. техн. наук А.Ю. Мишин.

Подп. в печ. Формат 60×84 1/16. Печать офсетная.

Печ. л. 8,5. Уч.-изд. л. 8,0. Тираж 200 экз. Зак. .

____________________________________________________________

Издатель: ОО «Ассоциация ученых» г. Арзамаса Нижегородской области,

607220, г. Арзамас, Нижегородской области, ул. Калинина, 19.

Участок офсетной печати: 607220, г. Арзамас, Нижегородской области, ул. Севастопольская, 15.

Содержание

Предисловие 5

Введение 6

1. Основные понятия систем 9

1.1. Основные понятия марковских систем 23

2. Динамические процессы и их свойства 24

2.1. Теорема проецирования 24

2.2. Импульсная теорема 25

2.3. Случайные процессы 25

3. Модели динамических систем и процессов 27

3.1 Формирующий фильтр стохастического процесса 30

3.1.1. Пример факторизации на основе Excel 31

3.2 Модели датчиков первичной информации 34

3.2.1. Пример составления динамической модели датчика 34

3.2.2 Формирование модели ДПИ методом ЖЛАХ 36

3.3. Основные матричные модели 38

3.3.1 Каноническое преобразование матричных моделей 40

3.3.1.1 Каноническое преобразование матричной модели в Excel 41

3.3.1.2. Алгоритм Сурье-Фадеева 44

3.4 Свойства матричных моделей 46

3.5 Методы формирования матричных моделей 48

3.5.1 Метод вспомогательной переменной 49

3.5.2. Метод нормальной матричной формы Коши 49

3.5.3. Метод канонического разложения 50

3.5.4. Метод разложения на простые множители 53

3.5.5. Метод аналогового моделирования 54

3.5.6 Нормальная форма записи уравнений состояния 55

4. Расчет основных характеристик процессов и систем 57

4.1. Дисперсия стохастического процесса через вычеты 57

4.2. Дисперсия стохастического процесса алгоритмом Острема 57

4.2.1. Реализация алгоритма Острема на основе Excel 58

4.3 Расчет частоты спектра и периода дискретности процесса 63

4.4. Расчет непрерывной и дискретной матричной модели 65

5. Статистическое моделирование систем 69

5.1. Оптимизация методом статистического моделирования 69

5.2. Объектно-ориентированное статистическое моделирование 72

5.3 Расчет передаточной функции ДС по заданным номинальным па-

раметрам и функциональным зависимостям

5.4. Преобразование модели “Передаточная

функция” в непрерывную

и дискретную матричные модели

5.5. Численное решение дифференциальных уравнений 78

5.6. М

етод статистического моделирования при определении допусков

на конструктивные параметры системы

5.7. Моделирование процессов с заданным законом распределения 81

6. Моделирование в системе MatLab Simulink 82

6.1. Общие сведения о системе моделирования MatLab Simulink 83

6.1.1. Библиотека блоков Simulink 85

6.2. Основные приемы подготовки и редактирования модели 97

6.3. Моделирование процесса в системе MatLab Simulink 99

6.3.1. Моделирование непрерывной системы контроля 101

6.3.2. Моделирование дискретной системы контроля 106

7. Примеры моделирования 109

7.1. Моделирование датчика при входном сигнале и аддитивном шуме 109

7.2. Моделирование процессов с заданными свойствами 111

8. Марковские процессы и системы 114

8.1. Марковские процессы

114

8.1.1. Основные свойства марковских систем 119

8.2. Уравнения Колмогорова для вероятностей состояний систем 123

8.3. Основные модели марковских систем 129

8.3.1. Фомула Литла 130

8.3.2. Функциональная схема многоканальной системы 131

8.3.3. Многоканальная система с отказами обслуживания 132

8.3.4. Многоканальная система с неограниченной очередью 133

8.3.5. Многоканальная система с ограниченной очередью 134

8.3.6. Одноканальная система с неограниченной очередью 136

8.3.7. Одноканальная система с ограниченной очередью 137

8.3.8. Одноканальная замкнутая система с m источниками заявок 137

8.4. Уравнения состояния резервированной системы в динамике

138

Заключение

141

Библиографический список 142

Предисловие

Опыт чтения лекций по курсу “Моделирование процессов и систем” для

различных специальностей предоставил автору возможность обобщить неко-

торые новые теоретические и практические вопросы моделирования в данном

учебном пособии. Существующий в настоящее время читательский интерес к

вопросам практического применения теории и методов моделирования про-

цессов и систем потребовал, в то же время, от автора рассматривать техноло-

гии моделирования в свете современного постоянно совершенствующегося

программного обеспечения и возрастающих ресурсов персональной компью-

терной техники.

Основной задачей учебного пособия является оказание поддержки сту-

дентам в освоении новых технологий моделирования в специализированных

отраслях знаний. Круг рассматривамых в учебном пособии вопросов, однако,

ограничен математическим и компьютерным моделированием для техниче-

ских систем. Студенты не технических специальностей также могут восполь-

зоваться предлагаемыми методами решения прикладных задач моделирования

и распространить приведенный здесь математический аппарат для своих задач.

Учебное пособие состоит из восьми разделов, первый из которых содер-

жит краткие общие положения теории систем. Второй раздел посвящен теории

динамических процессов и их свойствам.

В третьем разделе представлены сведение по практике математических

моделей на основе современной теории состояния систем и марковских про-

цессов. Приведен алгоритм эквивалентных матричных преобразований модели

системы к канонической форме. Этот раздел уже содержит ряд методик расче-

та математических моделей на основе удобного для этих целей лицензионного

программного обеспечения (ПО) электронных таблиц - MS Office Excel.

Четвертый раздел посвящен методикам расчета важных характеристик

процессов и систем. Здесь раскрыта, практически легко реализуемая, методика

расчета среднего квадрата отклонения процесса на основе алгоритма Острема.

Эта методика широко применяется далее во многих практических задачах ана-

лиза процессов и систем.

В пятом разделе представлены вопросы статистического моделирования

процессов и систем. Рассмотрено применение объектно-ориентированного

программного обеспечения для решения задач оптимизации динамических

характеристик ДПИ методом статистического моделирования, определение

допустимых отклонений параметров ДПИ при обеспечении их показателей

качества на заданном уровне.

Шестой раздел содержит сведения об особенностях моделирования про-

цессов и систем на основе лицензионного инженерного ПО Matlab. Приведены

наглядные примеры моделирования непрерывных и дискретных систем.

Седьмой раздел собрал ряд примеров прикладных задач моделирования

из учебной практики.

Большое внимание в восьмом разделе уделено марковским процессам и

системам. Здесь рассмотрены как теоретические вопросы, так и прикладные,

которые предполагают дальнейшую реализацию в лабораторных и практиче-

ских работах.

Автор старался соблюдать краткость изложения, и поэтому некоторые

интересные и важные вопросы представлены в ограниченном объеме. Развитие

вопросов моделирования для технических и других систем автор предполагает

продолжить и конкретизировать в методических указаниях по лабораторно-

практическим работам дисциплин по моделированию и измерительным систе-

мам.

Введение

Достижения в теории и практике моделирования процессов и систем, в

современных условиях, связано со стремительным развитием вычислительной

техники. Что казалось невозможным при решении многих задач моделирова-

нии еще несколько лет назад, сейчас легко реализуется на доступном инже-

нерном уровне [2 - 4]. Появление и развитие инженерных пакетов моделиро-

вания, таких как Matlab, Skylab, Labview, создало условия высокопризводи-

тельного, объектно-ориентированного моделирования на современных компь-

ютерах.

Задачи моделирования процессов и систем многообразны. Моделирова-

ние широко используется при инженерном проектировании и научных иссле-

дованиях: для решения технических и экономических задач, при исследовани-

ях в экологии и социологии, в приборостроении и автоматизации управления.

Особенности применения моделирования в приборостроении связаны в

первую очередь с технологическими достижениями в датчикостроении, теории

измерений и обработки информации.

В области экономических задач применение моделирования дает эффек-

тивный инструмент для управления проектами и прогнозирования развития

экономических процессов. Многие современные методы теории управления

оказались эффективными при решении экономических задач и достаточно лег-

ко реализуемыми на математических моделях и постановке вычислительных

экспериментов на компьютерной технике.

Развитие нейросетей, микросистемотехники, нанотехнологии внесло

много существенно нового в методы моделирования процессов и систем, что

дало также эффективный инструмент для предварительного решения задач

проектирования в математическом виде на моделях и их численном исследо-

вании на компьютерах.

Применение моделирования особенно эффективно при исследовании

проектируемых систем с целью изучения и прогнозировании различных явле-

ний и процессов в этих системах. Приближение к реальным условиям работы

проектируемых систем осуществляется при стохастическом моделировании,

когда к условиям моделирования добавляются случайные изменения парамет-

ров системы, возмущения и шумы измерений физических величин.

В приборостроении актуально моделирование задач управления, получе-

ния, передачи и преобразования информации. При этом современные модели

везде для описания процессов и систем используют дифференциальные урав-

нения и линейные матричные преобразования.

Развитие современных методов моделирования создало предпосылки для

создания и исследования высокоэффективных систем, которые, как правило,

ориентированы на цифровые алгоритмы обработки информации, с применени-

ем современных микропроцессоров, нейрокомпьютеров, процессоров с нечет-

кой логикой и других современных технологических достижений.

Появление миниатюрных устройств, в которых гальванические (элек-

трические) подсистемы интегрируются на микроуровне с механическими,

породило направление - МЭМС (микроэлектромеханические системы). В

России также МЭМС известны как «Микросистемная техника», содержа-

ние которой определено как: «Сверхминиатюрные механизмы, приборы,

машины с ранее недостижимыми массогабаритами, энергетическими по-

казателями и функциональными параметрами, создаваемые интегрально-

групповыми экономически эффективными процессами микро- и нанотехно-

логии». Это: микроэлектромеханические, микрооптоэлектро-

механические, микрофлюидные и микропневматические компоненты для

контрольно-измерительных, информационно-управляющих и телерадио-

коммуникационных систем; микромеханизмы и микромашины для гене-

рации, преобразования и передачи энергии и движения на микро и нано-

уровнях [5].

Моделирование МЭМС одно из направлений моделирования про-

цессов и систем.

Еще одно из перспективных направлений моделирования перспективных

технологических решений это нанотехнологии.

Нанотехнология механосинтеза позволяет набором веществ согласно оп-

ределенным алгоритмам с помощью наномеханизмов произвести сборку прак-

тически любого продукта. Помимо этого, механосинтез может также осущест-

влять обратный процесс, «разбирая» поданные на вход продукты до молеку-

лярного или атомарного уровня. Этот аспект технологии позволяет решить

проблему жизненного цикла.

Однако существует один важный параметр такой технологии– энергоем-

кость. Согласно статистике, в самом простом варианте производства при по-

мощи механосинтеза энергетические затраты составляют около 200 кВт часов

на 1 кг продукции. В случае сборки сложных устройств увеличение энергоза-

трат происходит за счет дополнительных модулей сепарации вещества на вхо-

де и его подачи на фронт сборки (принцип Plug & Play практически полностью

захватит этот сектор). Также для сложных устройств требуются такие вещест-

ва, которых мало или которые даже невозможно получить напрямую из окру-

жающей человека среды. Это касается, прежде всего, редкоземельных метал-

лов, используемых в электронике. Переработка же имеющихся в достатке эле-

ментов с помощью механосинтеза еще увеличит стоимость синтеза сложных

объектов. В этом случае происходит десятикратное увеличение энергозатрат.

Предельная стоимость производства 1 кг конечного продукта путем механо-

синтеза в итоге составляет около 2,2 тыс. современных рублей. Значительное

количество сложных технических устройств, изготавливаемых по традицион-

ным технологиям и используемых человеком, имеет более высокую стоимость

из расчета на 1 кг массы.

В предельном случае однородные объекты, производимые по нанотехно-

логиям, в конечном итоге, станут «условно-бесплатными» - их стоимость

практически на 100% будет состоять из энергозатрат.

Информация, как представляется, не может быть продуктом механосин-

теза ни прямо, ни опосредованно. В дополнение к этому, уже сейчас себестои-

мость производства информации находится на очень низком уровне. Можно

констатировать, что механосинтез никоим образом не влияет на стоимость

информации. Тем не менее, количество генерируемой информации значитель-

но увеличится за счет лавинообразного появления описаний процессов сборки

объектов, соответственно, объем информационного оборота возрастет (по за-

кону Мура в два раза каждые два года). Существующая сеть информационного

обмена может оказаться далекой от эффективности в таких условиях.

Нанотехнологии обещают разработать и запустить в массовое производ-

ство нанороботов, способных выполнять кажущиеся невозможными в настоя-

щее время задачи (в медицине, генной инженерии, нейротехнологиях).

В свете этих особенностей актуальным становится широкомасштабное

моделирование нанотехнологий и технологий механосинтеза, в том числе соз-

дание и исследование на компьютерах алгоритмов синтеза различных уст-

ройств. Суммируя сказанное о нанотехнологиях, надо учитывать при их моде-

лировании характерные особенности:

− существенное снижение издержек на производство и доставку боль-

шого количества материальных объектов;

− многократное увеличение информационного обмена;

− значительное увеличение жизненного цикла ресурсов;

− многократное увеличение энергопотребления.

На первый план при освоении нанотехнологий выходит моделирование

инновационных коммуникационных средств, моделирование перспективных

технологий обработки и передачи данных.

1. Основные понятия систем

Система - это комплекс взаимодействующих элементов, находящихся в

определенных отношениях друг с другом и со средой [6].

В определение понятия системы наряду с элементами, связями и их свой-

ствами и целями включают также наблюдателя. Популярно − система есть

множество входов, выходов, состояний, характеризуемых оператором перехо-

дов и оператором выходов:

S=(Х, Y, Z, H, G),

где Х - входы, Y - выходы, Z - состояния, Н - оператор переходов, G - оператор

выходов.

Для организационных систем в определении системы учитываются сле-

дующие компоненты:

S=(РL, RO, RJ, EX, PR, DT, SV, RD, EF),

где РL - цели и планы, RO - внешние ресурсы, RJ - внутренние ресурсы, ЕХ -

исполнители, PR - процесс, DТ - помехи, SV - контроль, RD - управление, ЕF -

эффект.

Под системой понимается объект, свойства которого не сводятся без ос-

татка к свойствам составляющих его дискретных элементов (неаддитивность

свойств). Интегративное свойство системы обеспечивает ее целостность, каче-

ственно новое образование по сравнению с составляющими ее частями.

Элемент системы можно рассматривать как самостоятельную систему

(математическую модель, описывающую какой - либо функциональный блок,

или аспект изучаемой проблемы), как правило более низкого порядка. Каждый

элемент системы описывается своей функцией. Если такой элемент обладает

внутренней структурой, то его называют подсистемой.

Информационно-измерительная система (ИИС) (рисунок 1.1) имеет дат-

чики первичной информации ДПИ, измеряющие физические величины; уст-

ройство обработки информации (УОИ) с фильтрами и вычислительными уст-

ройствами (ВУ). На основе измерений x

,...,x

, имеющих аддитивные шумы

,...,n

ИИС определяет оптимальные оценки X^=(x^

,...,x^

Рисунок 1.1. Информационно-измерительная система

Для систем важно понятие управления. В широком смысле слова под

управлением понимают организационную деятельность, осуществляющую

функции направленные на достижение определенных целей. Управление − это

организация такого целенаправленного воздействия на некоторую часть сре-

ды, называемую объектом управления (ОУ), в результате которого удовлетво-

ряются потребности субъекта, взаимодействующего с этим объектом. Упро-

щенное понятие управления – это получение, обработка информации и выра-

ботка управляющих воздействий для достижения объектом целей (стабилиза-

ция движение по программе, оптимизация движения).

Системы управления представляют собой особый класс динамических

систем, отличающихся наличием самостоятельных функций и целей управле-

ния и необходимым для реализации этих функций и целей высоким уровнем

специальной системной организации.

Следует заметить, что устройства связи и управления отличаются тем,

что энергетические отношения в них не играют существенной роли, а основ-

ным является способность передавать и перерабатывать информацию. Так в

линии связи ничтожная доля энергии излучаемой антенной передатчика полу-

чатся антенной приемника. КПД такого устройства, с точки зрения передачи

энергии, чрезвычайно мало.

Кибернетический подход к описанию систем состоит в том, что всякое

целенаправленное поведение рассматривается как управление. Язык управле-

ния — это использование понятий «объект», «среда», «обратная связь», «алго-

ритм».

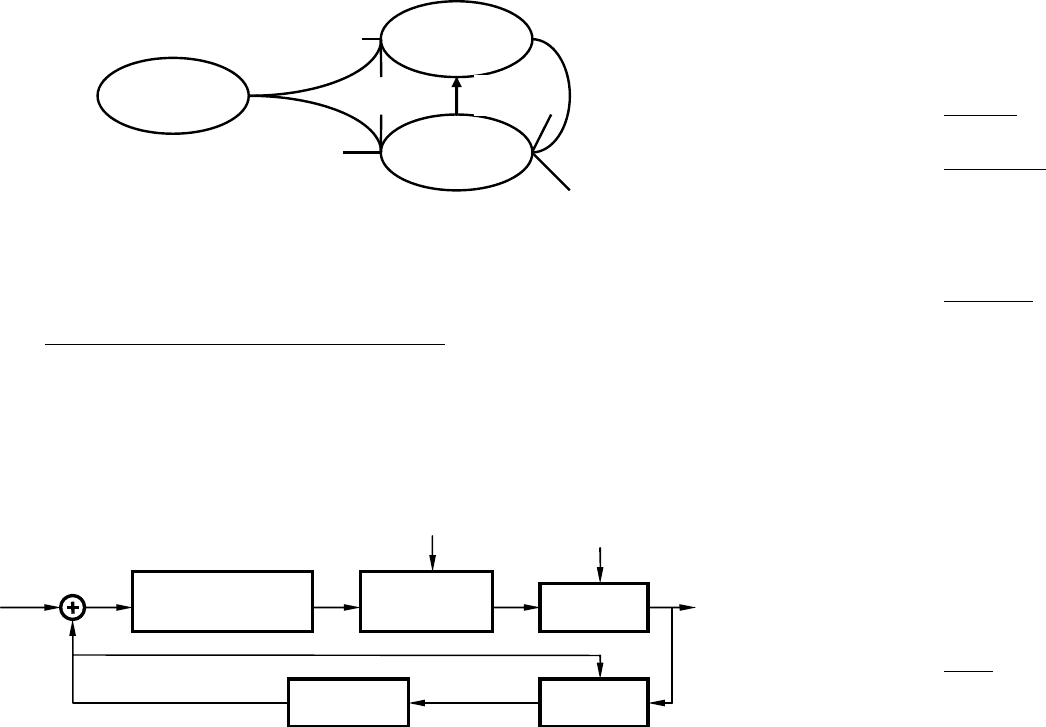
Анализ управления заставляет выделить тройку — среду, объект и субъ-

ект, внутри которой разыгрывается процесс управления (рисунок 1.2).

Среда

объект

субъект

Рисунок 1.2. Схема управления

В данном случае субъект ощущает на себе воздействие среды X и объ-

екта Y. Если состояние среды X он изменить не может, то состоянием объекта

Y он может управлять с помощью специально организованного воздействия U.

Система автоматического управления (САУ) - это комплекс устройств,

предназначенный для автоматического изменения одной или нескольких ре-

гулируемых величин объекта управления с целью поддержания желаемого

режима работы (цели управления). Целью управления может быть: стабилиза-

ция регулируемых величин, программное и следящее управление регулируе-

мых величин, оптимизация регулируемых величин. В САУ (рисунок 1.3) ис-

полнительное устройство и объект управления составляют объект наблюдения

и представляют динамику системы.

Исполнительное

устройство

Объект

управления

Датчики

Регулятор

Фильтр

Uoc=-LX(k/k)

X(k/k)

Uз

V(k)

N(k)

Y(k)

X(k)

Рисунок 1.3. Система автоматического управления

Случайный характер оцениваемых параметров и шумов измерений опре-

деляет вероятностный математический аппарат теории систем. В общем слу-

чае для описания поведения входных параметров и шумов используются плот-

ности вероятности. Параметры определяются априорной плотностью вероят-

ности f(X), где Х - вектор параметров. Шумы косвенно определяются плотно-

стью f(Y/X), где Y - вектор измерений. Вектор измерений связан с вектором

параметров Х линейным соотношением:

Y(t)=CX(t)+N(t),

где С - матрица состава измерений; N(t) - вектор аддитивных шумов измере-

ний.

Элемент. Под элементом принято понимать простейшую неделимую

часть системы (используется название "компонент").

Подсистема. Система может быть разделена на элементы не сразу, а по-

следовательным расчленением на подсистемы, которые представляют собой

компоненты более крупные, чем элементы, и в то же время более детальные,

чем система в целом. Названием "подсистема" подчеркивается, что такая часть

должна обладать свойствами системы (в частности, свойством целостности).

Структура. Это понятие происходит от латинского слова structure, озна-

чающего строение, расположение, порядок. Структура - это совокупность эле-

ментов и связей между ними. Структура может быть представлена графически,

в виде теоретико-множественных описаний, матриц, графов и других языков

моделирования структур.

Структуру часто представляют в виде иерархии. Иерархия - это упорядо-

ченность компонентов по степени важности (многоступенчатость, служебная

лестница). Между уровнями иерархической структуры могут существовать

взаимоотношения строгого подчинения компонентов (узлов) нижележащего

уровня одному из компонентов вышележащего уровня, т. е. отношения так

называемого древовидного порядка. Между уровнями иерархической структу-

ры могут существовать и более сложные взаимоотношения, например, типа

"страт", "слоев", "эшелонов". Примеры иерархических структур: энергетиче-

ские системы, АСУ, государственный аппарат.

Связь. Понятие "связь" входит в любое определение системы наряду с

понятием "элемент" и обеспечивает возникновение и сохранение структуры и

целостных свойств системы. Это понятие характеризует одновременно и

строение (статику), и функционирование (динамику) системы.

Связь характеризуется направлением, силой и характером (или видом).

По первым двум признакам связи можно разделить на направленные и нена-

правленные, сильные и слабые, а по характеру - на связи подчинения, генети-

ческие, равноправные (или безразличные), связи управления. Связи можно

разделить также по месту приложения (внутренние и внешние), по направлен-

ности процессов в системе в целом или в отдельных ее подсистемах (прямые и

обратные).

Важную роль в системах играет понятие "обратной связи". Это понятие,

легко иллюстрируемое на примерах технических устройств, не всегда можно

применить в организационных системах. Исследованию этого понятия боль-

шое внимание уделяется в кибернетике, в которой изучается возможность пе-

ренесения механизмов обратной связи, характерных для объектов одной физи-

ческой природы, на объекты другой природы. Обратная связь является осно-

вой саморегулирования и развития систем, приспособления их к изменяющим-

ся условиям существования.

Классификация систем. Системы разделяются на классы по различным

признакам, и в зависимости от решаемой задачи можно выбрать разные прин-

ципы классификации. При этом систему можно охарактеризовать одним или

несколькими признаками. Системы классифицируются следующим образом:

− по виду отображаемого объекта − технические, биологические и др.;

− по виду научного направления − математические, физические, хими-

ческие и т. п.;

− по виду формализованного аппарата представления системы — детер-

минированные и стохастические;

− по типу целеустремленности −открытые и закрытые;

− по сложности структуры и поведения − простые и сложные;

− по степени организованности − хорошо организованные, плохо орга-

низованные (диффузные), самоорганизующиеся системы.

Классификации всегда относительны. Так в детерминированной системе

можно найти элементы стохастических систем.

Цель любой классификации ограничить выбор подходов к отображению

системы и дать рекомендации по выбору методов.

Технические системы. Параметрами технических объектов являются

движущие объекты, объекты энергетики, объекты химической промышленно-

сти, объекты машиностроения, бытовая техника и многие другие. Объекты

технических систем хорошо изучены в теории управления.

Экономические объекты. Экономическими объектами являются: цех, за-

вод, предприятия различных отраслей. В качестве одной из переменных в них

выступают экономические показатели, например, прибыль.

Биологические системы. Живые системы поддерживают свою жизнедея-

тельность благодаря заложенным в них механизмам управления.

Детерминированные и стохастические системы. Системы, для которых

состояние системы однозначно определяется начальными значениями и мо-

жет быть предсказано для любого момента времени, называются детермини-

рованными.

Стохастические системы – системы, изменения в которых носят случай-

ный характер. Например, воздействие на энергосистему различных пользова-

телей. При случайных воздействиях данных о состоянии системы недостаточ-

но для предсказания в последующий момент времени.

Случайные воздействия могут прикладываться к системе извне или воз-

никать внутри некоторых элементов (внутренние шумы). Исследование сис-

тем при наличии случайных воздействий можно проводить обычными мето-

дами, минимизировав шаг моделирования, чтобы не пропустить влияния слу-

чайных параметров. При этом, так как максимальное значение случайной ве-

личины встречается редко (в основном в технике преобладает нормальное рас-

пределение), то выбор минимального шага в большинстве моментов времени

не будет обоснован.

В подавляющем большинстве случаев при проектировании систем зада-

ются не максимальным, а наиболее вероятным значением случайного парамет-

ра. В этом случае поучается более рациональная система, заранее предполагая

ухудшение работы системы в отдельные промежутки времени.

Расчет систем при случайных воздействиях производится с помощью

специальных статистических методов. Вводятся оценки случайных парамет-

ров, выполненные на основании множества испытаний.

Статистические свойства случайной величины определяют по ее функ-

ции распределения или плотности вероятности, или часто пользуются просто

статистическими характеристиками.

Открытые и закрытые системы. Основные отличительные черты откры-

тых систем - способность обмениваться с внешней средой энергией и инфор-

мацией. Закрытые (замкнутые) системы изолированы от внешней среды (с

точностью принятой в модели).

Плохо организованные системы. При представлении объекта в виде

«плохо организованной или диффузной системы» не ставится задача опреде-

лить все учитываемые компоненты, их свойства и связи между ними и целями

системы. Система характеризуется некоторым набором макропараметров и

закономерностями, которые находятся на основе исследования не всего объек-

та или класса явлений, а на основе определенной с помощью некоторых пра-

вил выборки компонентов, характеризующих исследуемый объект или про-

цесс. На основе такого выборочного исследования получают характеристики

или закономерности (статистические, экономические) и распространяют их на

всю систему в целом. При этом делаются соответствующие оговорки. Напри-

мер, при получении статистических закономерностей их распространяют на

поведение всей системы с некоторой доверительной вероятностью.

Подход к отображению объектов в виде диффузных систем широко при-

меняется при: описании систем массового обслуживания, исследовании пото-

ков информации в системах управления и т. д.

Самоорганизующиеся системы. Отображение объекта в виде самооргани-

зующейся системы — это подход, позволяющий исследовать наименее изу-

ченные объекты и процессы. Самоорганизующиеся системы обладают призна-

ками диффузных систем: стохастичностью поведения, нестационарностью

отдельных параметров и процессов. К этому добавляются такие признаки, как

непредсказуемость поведения; способность адаптироваться к изменяющимся

условиям среды, изменять структуру при взаимодействии системы со средой,

сохраняя при этом свойства целостности; способность формировать возмож-

ные варианты поведения и выбирать из них наилучший и др. Иногда этот

класс разбивают на подклассы, выделяя адаптивные или самоприспосабли-

вающиеся системы, самовосстанавливающиеся, самовоспроизводящиеся и

другие подклассы, соответствующие различным свойствам развивающихся

систем.

Примеры: биологические организации, коллективное поведение людей,

организация управления на уровне предприятия, отрасли, государства в целом,

т. е. в тех системах, где обязательно имеется человеческий фактор.

Простые и сложные кибернетические системы. В зависимости от способа

описания: детерминированного или теоретико-вероятностного А. И. Берг оп-

ределяет сложную систему как систему, которую можно описать не менее чем

на двух различных математических языках (например, с помощью теории

дифференциальных уравнений и алгебры Буля).

При разработке сложных систем возникают проблемы, относящиеся не

только к свойствам их составляющих элементов и подсистем, но также к зако-

номерностям функционирования системы в целом. При этом появляется ши-

рокий круг специфических задач, таких, как определение общей структуры

системы; организация взаимодействия между элементами и подсистемами;

учет влияния внешней среды; выбор оптимальных режимов функционирова-

ния системы; оптимальное управление системой и др.

Чем сложнее система, тем большее внимание уделяется этим вопросам.

Математической базой исследования сложных систем является теория систем.

В теории систем большой системой (сложной, системой большого масштаба,

Lage Scale Systems) называют систему, если она состоит из большого числа

взаимосвязанных и взаимодействующих между собой элементов и способна

выполнять сложную функцию.

Четкой границы, отделяющей простые системы от больших, нет. Деление

это условное и возникло из-за появления систем, имеющих в своем составе

совокупность подсистем с наличием функциональной избыточности. Простая

система может находиться только в двух состояниях: состоянии работоспо-

собности (исправном) и состоянии отказа (неисправном). При отказе элемента

простая система либо полностью прекращает выполнение своей функции, ли-

бо продолжает ее выполнение в полном объеме, если отказавший элемент ре-

зервирован. Большая система при отказе отдельных элементов и даже целых

подсистем не всегда теряет работоспособность, зачастую только снижаются

характеристики ее эффективности. Это свойство больших систем обусловлено

их функциональной избыточностью и, в свою очередь, затрудняет формули-

ровку понятия «отказ» системы. Наряду с этим в больших системах возможно

возникновение лавинообразных эффектов, когда небольшая “песчинка” вызы-

вает “обвал” целой системы. Эти эффекты относятся к странным аттракторам,

свойственным взаимодействию сложных систем. Изучаются теорией хаоса.

Под большой системой понимается совокупность материальных ресур-

сов, средств сбора, передачи и обработки информации, людей-операторов, за-

нятых на обслуживании этих средств, и людей-руководителей, облеченных

надлежащими правами и ответственностью для принятия решений. Матери-

альные ресурсы — это сырье, материалы, полуфабрикаты, денежные средства,

различные виды энергии, станки, оборудование, люди, занятые на выпуске

продукции, и т. д. Все указанные элементы ресурсов объединены с помощью

некоторой системы связей, которые по заданным правилам определяют про-

цесс взаимодействия между элементами для достижения общей цели или

группы целей.

Примеры больших систем: информационная система; пассажирский

транспорт крупного города; производственный процесс; система управления

полетом крупного аэродрома; энергетическая система и др.

Характерные особенности больших систем − это: 1) большое число эле-

ментов в системе (сложность системы); 2) взаимосвязь и взаимодействие меж-

ду элементами; 3) иерархичность структуры управления; 4) обязательное на-

личие человека в контуре управления, на которого возлагается часть наиболее

ответственных функций управления.

Сложность системы. Пусть имеется совокупность из n элементов. Если

они изолированы, не связаны между собой, то эти n элементов не являются

системой. Для изучения этой совокупности достаточно провести не более чем

n исследований с каждым элементом. В общем случае в системе со взаимны-

ми связями между компонентами необходимо исследовать n(n-1) связей. Если

состояние каждой связи охарактеризовать в каждый момент времени наличием

или отсутствием, то общее число состояний системы будут равно 2

n(n-1)

. На-

пример, если n=10, то число связей n(n-1)=90, число состояний 2

≈1,3*10

Изучение такой системы путем непосредственного обследования ее со-

стояния оказывается весьма сложным. Следовательно, необходимо разрабаты-

вать компьютерные методы, позволяющие сокращать число обследуемых со-

стояний. Сокращение числа состояний БС — первый шаг в формальном опи-

сании систем.

Взаимосвязь и взаимодействие между элементами в БС. Разделение сис-

темы на элементы — второй шаг при формальном описании системы. Внут-

ренняя структура элемента при этом не является предметом исследования.

Имеют значение только свойства, определяющие его взаимодействие с други-

ми элементами системы и оказывающие влияние на характер системы в целом.

В качестве подсистем рассматриваются некоторые более или менее самостоя-

тельно функционирующие части системы. Разделение на элементы и подсис-

темы может быть произведено различными способами.

В системе управления полетом самолета можно выделить следующие

подсистемы: систему дальнего обнаружения и управления; систему дальней

связи; систему слепой посадки и взлета самолета; систему диспетчеризации;

бортовую аппаратуру самолета.

Выделение подсистем — третий важный шаг при формальном описании

больших ситем.

Поскольку в БС обязательно наличие человека, она является всегда эрга-

тической системой. Часть функций управления выполняется человеком. Эта

особенность БС связана с целым рядом факторов:

− участие человека в БС требует, чтобы управление учитывало социаль-

ные, психологические, моральные и физиологические факторы, которые не

поддаются формализации и могут быть учтены в системах управления только

человеком;

− необходимость в ряде случаев принимать решение на основе неполной

информации, учитывать неформализуемые факторы.

Шкалы времени. Другим важным аспектом динамической сложности яв-

ляется вопрос о различных шкалах времени для различных частей процесса.

Бывает, что скорости изменения компонент одного и того же процесса различ-

ны: одни компоненты изменяются быстрее, другие – медленнее.

Типичным примером такого процесса является регулирование уровня во-

ды в системе водохранилищ. Для управления на уровне индивидуального рас-

пределения воды требуется принимать решения ежедневно (или даже ежечас-

но), хотя решение об общем потоке воды через вход-выход принимается раз в

месяц или раз в квартал.

Проблема различных шкал времени напоминают проблему интегрирова-

ния “жестких” систем ДУ или когда имеем дело с некорректной проблемой.

Весьма актуальным является оценка степени целостности системы при

переходе из одного состояния в другое. В связи с этим возникает двойственное

отношение к закономерности целостности. Ее называют физической аддитив-

ностью, независимостью, суммативностью, обособленностью. Свойство физи-

ческой аддитивности проявляется у системы, как бы распавшейся на незави-

симые элементы. Строго говоря, любая система находится всегда между край-

ними точками как бы условной шкалы: абсолютная целостность — абсолют-

ная аддитивность, и рассматриваемый этап развития системы можно охаракте-

ризовать степенью проявления в ней одного или другого свойства и тенденци-

ей к его нарастанию или уменьшению.

Интегративными называют системообразующие, системосохраняющие

факторы, важными среди которых являются неоднородность и противоречи-

вость ее элементов.

Коммуникативность. Система не изолирована, она связана множеством

коммуникаций со средой, которая не однородна, а представляет собой сложное

образование, содержит надсистему (или даже надсистемы), задающую требо-

вания и ограничения исследуемой системе, подсистемы и системы одного

уровня с рассматриваемой.

Иерархическая упорядоченность пронизывает все, начиная от атомно-

молекулярного уровня и кончая сложными системами. Иерархичность как за-

кономерность заключается в том, что закономерность целостности проявляет-

ся на каждом уровне иерархии. Благодаря этому на каждом уровне возникают

новые свойства, которые не могут быть выведены как сумма свойств элемен-

тов. При этом важно, что не только объединение элементов в каждом узле

приводит к появлению новых свойств, которых у них не было, и утрате неко-

торых свойств элементов, но и что каждый член иерархии приобретает новые

свойства, отсутствующие у него в изолированном состоянии.

На каждом уровне иерархии происходят сложные качественные измене-

ния, которые не всегда могут быть представлены и объяснены. Но именно бла-

годаря этой особенности рассматриваемая закономерность приводит к инте-

ресным следствиям. Во-первых, с помощью иерархических представлений

можно отображать системы с неопределенностью.

Во-вторых, построение иерархической структуры зависит от цели: для

многоцелевых ситуаций можно построить несколько иерархических структур,

соответствующих разным условиям, и при этом в разных структурах могут

принимать участие одни и те же компоненты.

В-третьих, даже при одной и той же цели, если поручить формирование

иерархической структуры разным исследователям, то в зависимости от их

предшествующего опыта, квалификации и знания системы они могут получить

разные иерархические структуры, т. е. по-разному разрешить качественные

изменения на каждом уровне иерархии.

Эквифинальность характеризует предельные возможности систем опре-

деленного класса сложности. Потребность во введении этого понятия возника-

ет начиная с некоторого уровня сложности, например, для биологических сис-

тем.

В настоящее время не исследован ряд вопросов этой закономерности: ка-

кие именно параметры в конкретных системах обеспечивают свойство экви-

финальности, как обеспечивается это свойство, как проявляется закономер-

ность эквифинальности в организационных системах.

Жизненный цикл - время является непременной характеристикой систе-

мы – это свойство историчности. Для технических и организационных систем

определить жизненный цикл довольно трудно.

Основа закономерности историчности — внутренние противоречия меж-

ду компонентами системы. Но как управлять развитием или хотя бы понимать

приближение соответствующего периода развития системы — эти вопросы

еще мало исследованы.

В последнее время на необходимость учета закономерности исторично-

сти начинают обращать больше внимания. В частности, в системотехнике при

создании сложных технических комплексов требуется на стадии проектирова-

ния системы рассматривать не только вопросы разработки и обеспечения раз-

вития системы, но и вопрос, как и когда нужно ее уничтожить. Например, спи-

сание техники, особенно сложной — авиационной, «захоронение» ядерных

установок и др.

Система должна удовлетворять закону необходимого разнообразия. Его

впервые сформулировал У.Р. Эшби: чтобы создать систему, способную спра-

виться с решением проблемы, обладающей определенным, известным разно-

образием, нужно, чтобы сама система имела еще большее разнообразие, чем

разнообразие решаемой проблемы, или была способна создать в себе это раз-

нообразие. Этот закон достаточно широко применяется на практике. Он по-

зволяет, например, получить рекомендации по совершенствованию системы

управления предприятием, объединением, отраслью.

Закономерность осуществимости и потенциальной эффективности сис-

тем. Исследования взаимосвязи сложности структуры системы со сложностью

ее поведения позволили получить количественные выражения предельных

законов для таких качеств системы, как надежность, помехоустойчивость,

управляемость и др. На основе этих законов оказалось возможным получение

количественных оценок порогов осуществимости систем с точки зрения того

или иного качества, а объединяя качества — предельные оценки жизнеспособ-

ности и потенциальной эффективности сложных систем.

Применения системных представлений для анализа сложных объектов и

процессов рассматривают системные направления, включающие в себя: сис-

темный подход, системные исследования, системный анализ (системологию,

системотехнику и т. п.).

Системный подход. Исследования объекта с разных сторон, комплексно.

Термин «системный подход» практически используется вместо терминов

«комплексный подход».

Метод экспертной оценки, известен в литературе как «метод Дельфи».

Название связано с древнегреческим городом Дельфи, где при храме Аполлона

с IX в. до н.э. до IV в. н.э. по преданиям существовал Дельфийский оракул.

Суть метода Дельфи заключается в следующем. В отличие от традицион-

ного подхода к достижению согласованности мнений экспертов путем откры-

той дискуссии метод Дельфи предполагает полный отказ от коллективных об-

суждений. Это делается для того, чтобы уменьшить влияние таких психологи-

ческих факторов, как присоединение к мнению наиболее авторитетного спе-

циалиста, нежелание отказаться от публично выраженного мнения, следование

за мнением большинства. В методе Дельфи прямые дебаты заменены тщатель-

но разработанной программой последовательных индивидуальных опросов,

проводимых обычно в форме анкетирования. Ответы экспертов обобщаются и

вместе с новой дополнительной информацией поступают в распоряжение экс-

пертов, после чего они уточняют свои первоначальные ответы. Такая процеду-

ра повторяется несколько раз до достижения приемлемой сходимости сово-