Волков В.Л. Моделирование процессов и систем в приборостроении
Подождите немного. Документ загружается.


41
det[sI-A] =s
n
+g
n-1
s
n
+…+g
0
= 0.
3) Определяется матрица A' в виде
A' = Ф
T
.
4) Вычисляется матрица линейного преобразования К
=
−
00...0
......
0...
...
32
121
n
n
nn
g
ggg
gggg
K
.
5) Вычисляется матрица C' в виде
C' = KC
T
.
3.3.1.1. Каноническое преобразование матричной модели в Excel
Рассмотренный алгоритм легко реализуется с помощью электронных
таблиц Microsoft Excel.
Рассмотрим конкретный пример динамической системы, матричная мо-
дель которой получена на основе анализа физики движения объекта.
Пример. Вращательное движение ЛА в вертикальной плоскости задаётся
в виде системы непрерывных дифференциальных уравнений и уравнений из-
мерения.
Уравнения движения ЛА в продольной плоскости имеют вид [15].
=θ+ϑ+θ
δ=θ−ϑ+ϑ+ϑ
,aa
;aaaa
b
0
44
3221
&
&&&
(3.13)
где ϑ – угол тангажа; θ – угол наклона вектора скорости к горизонту; δ
в
– угол
отклонения руля высоты; a
i
– динамические коэффициенты, зависящие от аэ-
родинамических параметров самолёта.
Вводя новые обозначения для переменных (x
1
=ϑ, x
2
=ϑ', x
3
= θ), запишем
систему (3.13) в нормальной форме Коши:
42
+=
δ+++=
=
,xaxax
;axaxaxax
xax
b
3331313
33232221212
2121
&
&
&
(3.14)
где а
12
=-1, а
21
=-а
2
, а
22
=-а
1
, а
23
=а
2
, а
31
=а
4
, а
33
=-а
4
.
Система уравнений (3.14) в векторно–матричной форме имеет вид
,b
BAXX δ+=
&
(3.15)
где
;
321
T
xxxX =
T
aB 00
3
=
;
.
0
00
2331
232221
12
aa
aaa
a
A =
Реальные значения аэродинамических коэффициентов для легкого ЛА
a
2
=4,2, a
1
=1,76, a
2
=4,2, a
4
=0,77, a
3
=-7,4.
Уравнения измерений y
1
=x
2
’+n
1
, y
2
=x
3
+n
2,
где n
1
, n
2
- белые гауссовские
шумы с интенсивностями R
11
, R
22
. Матричные уравнения движения и измере-
ний X'=AX+BU, Y=CX+N,
где матрицы A, B, D, C имеют вид:
=
=
−
−−
−
=
1 0 0
0 1 0
,
0
7,4-
0
,
77,0077,0
2,476,12,4
010
CBA
.
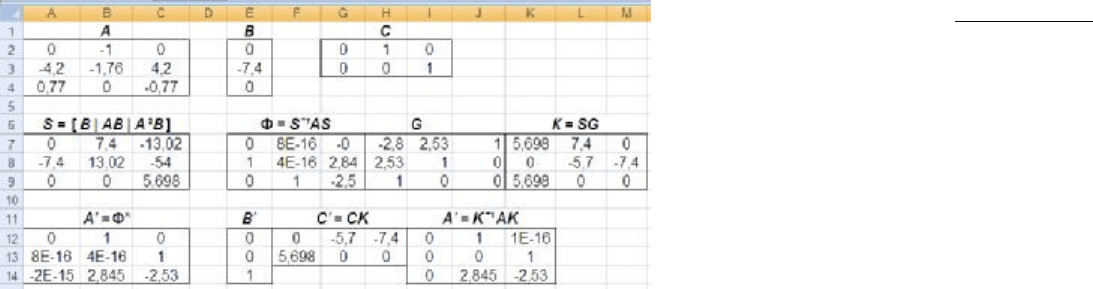
В электронной таблице Excel (см. рис.3.11) строки 2-4 содержат исход-
ные данные. В строках 7-9 запрограммированы основные матричные формулы
канонического преобразования S, Ф, G, K.
S´ A7:A9 =E2:E4
S´ B7:B9 =МУМНОЖ(A2:C4;E2:E4)
S´ C7:C9 =МУМНОЖ(МУМНОЖ(A2:C4;A2:C4);E2:E4)
Ф´ E7:G9 =МУМНОЖ(МУМНОЖ(МОБР(A7:C9);A2:C4);A7:C9)
K´ K7:M9 =МУМНОЖ(A7:C9;H7:J9) .
43
Рисунок 3.11. Алгоритм канонического преобразования в Excel
Результаты канонического преобразования с помощью матриц S, Ф, G, K
получены в строках 12-14.
A´ A12:C14 =ТРАНСП(E7:G9)
C´ F12:H14 =МУМНОЖ(G2:I3;K7:M9)
A´ I12:K14 =МУМНОЖ(МОБР(K7:M9);МУМНОЖ(A2:C4;K7:M9))
Коэффициенты матрицы G для вычисления K берутся из матрицы Ф.
3.3.1.2. Алгоритм Сурье-Фадеева для определения коэффициентов
Алгоритм Сурье-Фадеева позволяет вычислить коэффициенты характе-
ристического полинома квадратной матрицы независимо от вычисления мат-
рицы Ф (это бывает необходимо для получения канонического преобразования
в другой матричной форме). Такая же задача часто возникает и при проектиро-
вании матричных моделей нетрадиционного вида.
Теория Сурье-Фадеева [16] говорит о том, что для любой невырожденной
квадратной матрицы А размером n
x
n коэффициент g
n-k
характеристического
полинома: s
n
+g
n-1
·s
n-1
+...+g
1·
s+g
0
и матричный коэффициент C
n-k
матрицы
adj(sI-A) в уравнении adj(sI-A)=C
n-1
s
n-1
+C
n-2
s
n-2
+...+C
1
s+C
0
удовлетворяют
при k=1,...,n следующим соотношениям:
C
n-k-1
=C
n-k
A+g
n-k
I, C
n-k
=I, C
-1
=0, (3.16)
g
n-k
=-(1/k)spur(C
n-k
A). (3.17)
44
Доказательство. Рекуррентная формула (3.16) вытекает непосредст-
венно из системы уравнений
s
n
: I= C
n-1
,
s
n
-
1
: g
n-1
I= -C
n-1
A+C
n-2
,
s
0
: g
1
I= -C
1
A+C
0
,
s
0
: g
0
I= -C
0
A .
При k=n выражение (3.17) может служить для проведения численного
контроля. Доказательство формулы следует из соотношений:
det(sI-A)=spur adj(sI-A). (3.18)
В левой части здесь стоит производная по s характеристического много-
члена; правая же часть преобразуется в соответствии с (3.18). Приравнивая
коэффициенты при степенях S
n-k-1
, получаем (nk) g
nk
=spurC
n-k-1
, k=0,...,n-1.
Отсюда вытекает (3.17) с помощью подстановки (3.16).
Формулы (3.16) и (3.17) представляют собой простой способ вычисле-
ния выражений det(sI-A) и adj(sI-A). А соотношение: (sI-A)
-1
=[det(sI-A)]
-1
adj(sI-
A) дает обратную матрицу (sI-A)
-1
, соответствующую преобразованию Лапласа
переходной матрицы дифференциального уравнения
X'=Ax(t).
3.3.1.3. Продолжение примера
Вычисление коэффициентов характеристического полинома квадратной
матрицы A на основе алгоритма Сурье-Фадеева легко программируется в
электронной таблице Excel. Строки 18-20 и 34-36 в электронной таблице (см.
рис.3.12) заполняются вручную на основании исходных данных. Также по ис-
ходным данным заполняется блок матрицы C
-1
(ячейки A30-C32). Затем в
строках 22-24 реализуются матричные формулы (коэффициенты характери-
стического полинома в электронной таблице Excel обозначены через α
i
).
A22:C24 =МУМНОЖ(A18:C20;E$2:G$4)+A$34:C$36*E22
E22 =-СУММ(H24;G23;F22)/A21
F22:H24 =МУМНОЖ(A18:C20;E$2:G$4).
Ввод формул в строки 26-28, осуществляется путем простого копирова-
ния строк 22-24.

45
Рисунок 3.12. Алгоритм Сурье-Фадеева в Excel
В результате копирования строк 22-24 получаются результаты в строках
26-28 и 30-32 (см. рис.3.13). Это эффект относительной и абсолютной адреса-
ции Excel.
Рисунок 3.13. Алгоритм Сурье-Фадеева в Excel (продолжение)
Задача решена! Получены коэффициенты характеристического полинома
матричной модели, которые могут быть использованы для канонического пре-
образования. Полная картина алгоритма Сурье-Фадеева представлена на сле-
дующей скрин-копии (рисунок 3.14).
46
Рисунок 3.14. Алгоритм Сурье-Фадеева в Excel (окончание)
3.4. Свойства матричных моделей
В общем виде детерминированная математическая модель линейной ста-
ционарной динамической системы представляется либо в виде одного уравне-
ния
),(
)(
)(
)(
0010
tf
dt
tfd
tgb
dt
tgd
bya
dt
dy
a
dt
yd
a
r
r
r
m
m
m
nn
n
n
β++β+++=+++
−
KKK
(3.19)
либо в виде системы уравнений, приведённой к нормальной форме Коши:
+++=
+++=
+++=
.xaxaxax
;xaxaxax
;xaxaxax
nnnnnn
nn
nn
K
&
KKKKKKKKKKKKK
K
&
K
&
2211
22221212
12121111
(3.20)
Причём в правых частях не обязательно присутствуют все n переменных,
т.е. часть из коэффициентов a
i j
равны нулю. В то же время в некоторых урав-
нениях добавляются задающие g
i
(t) и возмущающие v
i
(t) воздействия.
Характеристическое уравнение такой системы имеет вид

47
,0)(
21
22221
11211
=
λ−
λ−
λ−
=λ
nnnn
n
n
aaa
aaa
aaa
D
L
LLLL
L
L
(3.21)
или в развёрнутом виде
.aaaa
nn
nn
0
1
1
10
=+λ++λ+λ
−
−
K
(3.22)
Как отмечалось выше, система уравнений (3.20) может быть записана и в
матричной форме
,AXX =
&
(3.23)
а её характеристическое уравнение (3.21) соответственно в виде
,0)det()(
=
λ
−
=
λ
E
A
D
(3.24)
где
,E,
aaa
aaa
aaa
A
nnnn
n
n
100
010
001
21
22221
11211
K
KKKK
K
K
K
KKKK
K
K
==
λ
i
- корни характеристического уравнения (полюсы передаточной функ-
ции), называемые в матричном исчислении собственными значениями или
характеристическими числами матрицы A. Матричная запись уравнений весь-
ма удобна и для представления математических моделей систем в области
изображений по Лапласу. При этом практически все формулы для преобразо-
ваний по Лапласу скалярных переменных справедливы и для случая матриц.
Обозначим через X(s) n-мерный вектор состояния в области изображений Лап-
ласа, через U(s) – p-мерный вектор входных переменных и через Y(s) m-
мерный вектор выходных переменных. Соотношение между этими векторами
устанавливается передаточными матрицами H(s) и W(s) типа n × m и r × m в
виде
),()()(
s
U
s
H
s
X
=
(3.25)
),()()( sUsWsY
=
(3.26)
48
откуда следует, что элемент h
i j
матрицы H(s) представляет собой преоб-
разования по Лапласу импульсной переходной функции по i-й координате со-
стояния относительно j-го входного сигнала при равенстве нулю всех других
входных сигналов.
Рассмотрим взаимосвязь между передаточными матрицами Н(s), W(s) и
матрицами во временной области A, B и C , для чего применим к математиче-
ской модели объекта преобразование Лапласа:
=
+=−
).()(
);()()0()(
sCXsY
sBUsAXxssX
Если принять начальные условия нулевыми, т.е. x(0)=0, то вводя понятие
единичной матрицы I , получаем sX(s)-AX(s)=BU(s) и далее (sI-A)X(s) = BU(s).
Окончательно
).()()(),()()(
11
sBUAsICsYsBUAsIsX
−−
−=−=
(3.27)
В соответствии с (3.27) имеем
;)()(
1
BAsIsH
−
−=
(3.28)
,)()(
1
BAsICsW
−
−=
(3.29)
где (sI-A)
-1
есть обратная матрица по отношению к матрице (sI-A), равная на
основании правил матричного исчисления отношению присоединённой мат-
рицы
)'(
A
sI
−
к определителю матрицы (sI-A), т.е.
.
)det(
)'(
)(
1
AsI
AsI
AsI
−
−
=−
−
Рассмотренный выше алгоритм Сурье-Фадеева, позволяет без труда на-
ходить обратную матрицу и получать, таким образом, все рассмотренные здесь
передаточные функции и в целом решение дифференциальных уравнений от-
носительно любой из компонент вектора состояния и относительно выхода.
3.5. Методы формирования матричных моделей
Рассмотрим всего несколько методов определения детерминированных
математических моделей, выраженных через координаты состояния для ли-
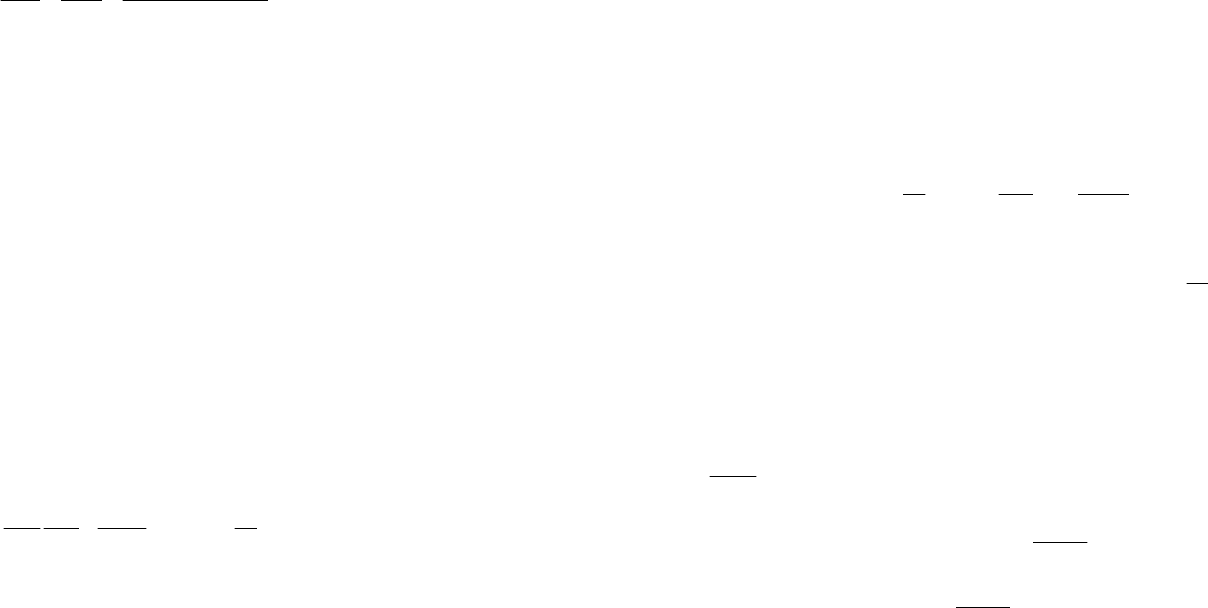
49
нейных стационарных систем при условии, если заданы их передаточные
функции или дифференциальные уравнения вида
).()()()(
s
u
s
B
s
y
s
D
=
Это, прежде всего метод вспомогательной переменной и метод нормаль-
ной формы Коши [1]. Для этих методов рассматриваем передаточную функ-
цию в виде
.
...
...
)(
)(
)(
)(
)(
10
10
n
n
m
m
sdsdd
sbsbb
sD
sB
sU
sY
sW
+++
+++
===
(3.30)
Соответствующее дифференциальное уравнение определяется на основе
свойств преобразования Лапласа: d
n
y
(n)
(t)+...+d
0
y(t)=b
m
u
(m)
(t)+...+b
0
u(t).
3.5.1. Метод вспомогательной переменной
Модель в пространстве состояний методом вспомогательной переменной
формируется при обозначении y(s)=B(s)/D(s), где B(s), D(s) полиномы соответ-
ственно степени m и n. При замене переменной R(s)=u(s)/D(s), получится
дифференциальное уравнение относительно R(t) без производных в правой
части d
n
R
(n)
+...+d
0
R=u(t). При этом выражение для y(t) также не содержит
производных в правой части: b
m
R
(m)
+...+b
0
R=y(t).
Матричная модель при этом представляется уравнением состояния и
уравнением выхода: X′=AX+Du, y(t)=CX, где матрицы A, D, C
cоответственно равны:
,
1
...
0
,
...
...
0 ... 1 0
110
=
−−−
=
−
nn
n
nn
d
D
d
d
d
d
d
d
A
(3.31)
[
]
0 ..0 ,...
0 m
bbC
=
.
Полученная матричная модель является универсальной, легко реализуе-
мой при моделировании на компьютере. Недостатком метода является необхо-
димость того, что порядок числителя исходной передаточной функции должен
быть меньше порядка знаменателя.
3.5.2. Метод нормальной матричной формы Коши
Теория формирования матричной модели методом нормальной формы
Коши подробно рассмотрена в [1]. Здесь приводятся лишь основные соотно-
50
шения, требуемые для реализации матричной модели. Универсальные матрич-
ные уравнения имеют традиционный вид: X′=AX+BU, y=CX, где матрица A,
определяется из соотношения (3.31), а матрицы B и C имеют вид:
[ ]
, 1,0,...,0= ,
....
....
0
C
C
CB
n
mn
=
−
(3.32)
где коэффициенты матрицы B определяются следующими соотношениями:
∑
−
=
+−−
−==
1
0
0
,
j
k
k
n
kjn
n
jn
j
n
n
C
a
a
a
b
C
a
b
C
. (3.33)
Выходной сигнал системы в общем случае:
).()(
1
tu
a
b
xty
n
n
+=
3.5.3. Метод канонического разложения
Вначале для простоты положим, что M(s)=1, а характеристическое урав-
нение D(λ)=0 имеет простые корни λ
i
. В этом случае
,
)(
1
u
pD
y =
а
∏
=
λ−=
n
i
i
ppD
1
)()(
, откуда после разложения на простые дроби
).()(
1
tu
p
c
ty
n
i
i
i
λ−
=
∑
=
(3.34)
Если положить, что
)(
1
)( tu
p
tx
i
i
λ−
=
, то
.)()(
1
∑
=
=
n
i
ii
txcty (3.35)
Согласно уравнению (3.35) переменная x
i
удовлетворяет дифференциаль-
ному уравнению первого порядка:
,,,2,1, niuxx
iii
K
&
==λ−
(3.36)

51
а это значит, что уравнение (3.36) эквивалентно уравнению состояния вида
(3.14), т.е.
,
=
+=
CXy
BUAXX
&
(3.37)
где
.,
1
1
1
,
00
00
00
21
2
1
n
n
cccCBA L
M
L
LLLL
L
L
==Λ=
λ
λ
λ
=
На рисунке 3.15 представлена структурная схема системы, соответст-
вующая уравнениям (3.37). Хотя данный способ справедлив как для действи-
тельных, так и для комплексных корней λ
i
, применять его в последнем случае
не рекомендуется, так как вводить в рассмотрение комплексные координаты
состояния весьма неудобно.
Если характеристическое уравнение имеет кратные корни или переда-
точная функция имеет нули (m≠ 0), то метод разложения на простые дроби
остается справедливым. Для нестационарных систем метод канонического
разложения не применяется.
Рисунок 3.15. Схема формирования модели системы каноническим методом
Пример. Дана передаточная функция системы
52
)1()1(
)(
2
2
1
2
2
1
++
=
sTsT
TT
sW
и
.
1
,
1
2
3
1
2,1
TT
−
=λ
−
=λ
Требуется: найти уравнения состояния и передаточную матрицу. Пред-
ставим передаточную функцию через собственные значения в виде суммы
простых дробей.
.
)()(
)())(()(
)()()()()(
1
)1()1(
)(
3
2
1
2
1331231
3
3
1
2
2
1
1
3
2
12
2
1
2
2
1
λ−λ−
λ−+λ−λ−+λ−
=
=
λ−
+
λ−
+
λ−
=
λ−λ−
=
++
=
ss
scsscsc
s
c
s
c
s
c
sssTsT
TT
sW
Коэффициенты находятся из соотношений
;1)())(()(
2
1331231
=λ−+λ−λ−+λ− scsscsc
.
)(
1
,
1
3
2
31
2
31
1
ccc −=
λ−λ
−
=
λ−λ
=
Таким образом, имеем
+λ=
+λ=
+λ=
uxx
uxx
xxx
333
222
2111
&
&
&
или
,
1
1
0
00
00
00
3
2
1
3
2
1
3
2
1
u
x
x
x
x
x
x
+⋅
λ
λ
λ
=
&
&
&
а наблюдаемая переменная
.
321
Xcccy =
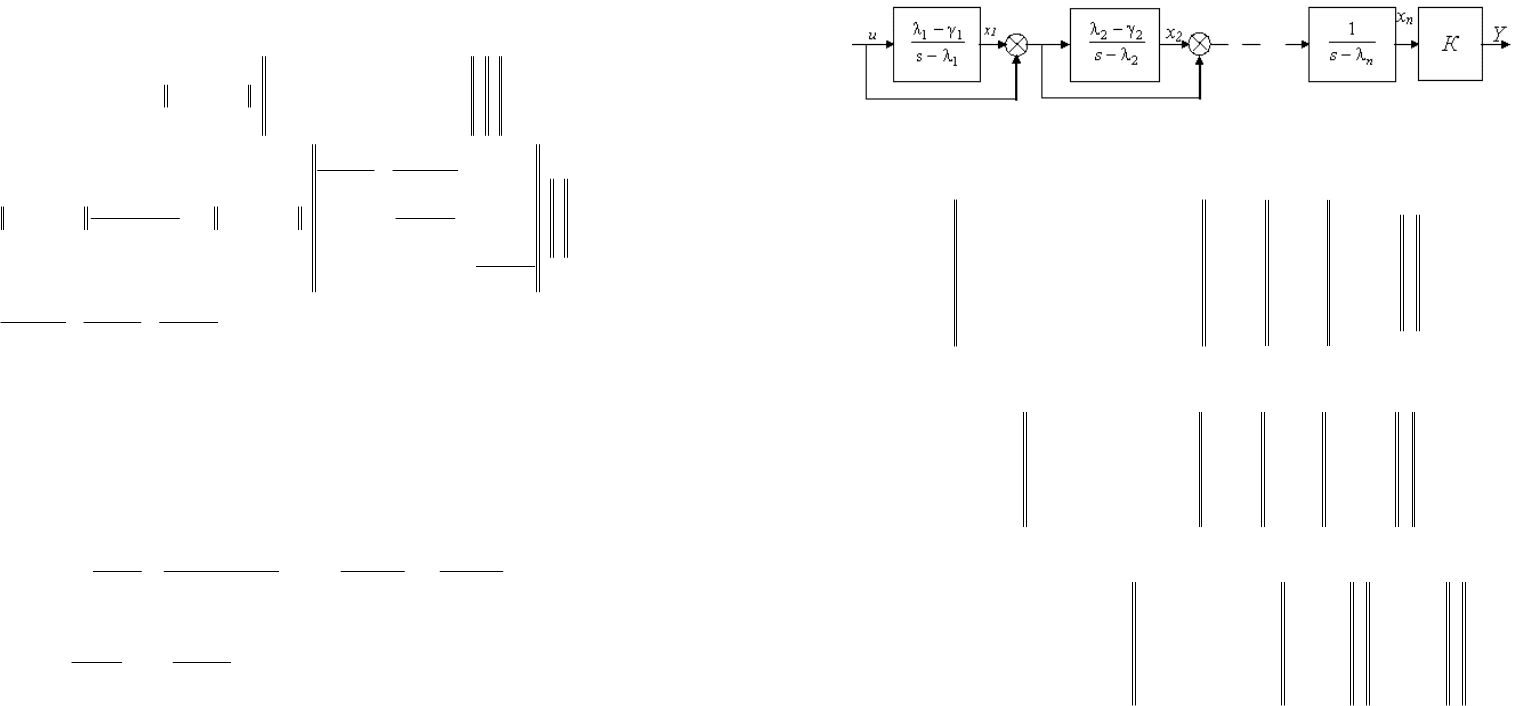
На рисунке 3.16 представлена структурная схема заданной системы, ма-
тематическая модель которой получена в канонической форме.
Рисунок 3.16. Схема формирования модели для примера
53
Передаточную матрицу найдем в следующем виде.
)(
)()()(
1
1
0
)(
1
00
0
)(
1
0
0
)(
1
)(
1
)det(
)
~
(
1
1
0
)(00
0)(0
01)(
)()(
3
3
1
2
2
1
1
3
2
2
11
321321
3
2
1
321
1
sW
s
c
s
c
s
c
s
s
ss
cccB
AsE
AEs
ccc
s
s
s
cccBAsECsW
=
λ−
+
λ−
+
λ−
=
=⋅
λ−
λ−
λ−λ−
⋅=
−
−
=
=⋅
λ−
λ−
−λ−
⋅=−=
−
3.3.4. Метод разложения на простые множители
Известно, что передаточную функцию системы можно выразить через ее
нули γ
i
, и полюсы λ
i
, т.е.
∏ ∏
= +=
λ−λ−
γ−
=
++
++
==
m
i
n
mi
ii
i
n
n
m
m
ss
s
k
asa
bsb
sD
sM
sW
1 1
0
0
)(
1
)(
)(
)(
)(
)(
L
L
. (3.38)
Так как
i
ii
i
i
ss
s
λ−
γ
−
λ
+=
λ−
γ
−
1
, то структурная схема системы, соответст-
вующая передаточной функции (3.38), принимает вид, представленный на ри-
сунке 3.17, а уравнения состояния будут
=
+λ=
γ+λ+γ−λ+λ=
γ−λ+λ=
−
n
nnnn
kxy
xxx
uxxx
uxx
;
;)()(
;)(
1
22122222
11111
&
LLLLLLLLLLLLLLLLL
&
&
(3.39)
54
Рисунок 3.17. Схема формирования модели
или в соответствии с (3.38)
.
0
0
,
0
,
000
00
00
000
33
22
11
333
222
1
k
CBA
T
n
M
L
L
LLLLL
L
L
L
=
γ−λ
γ−λ
γ−λ
=
λ
λγ−λ
λγ−λ
λ
=
(3.40)
Например, при n= 4, m= 2
.
0
0
0
,
0
0
,
100
010
00
000
22
21
4
3
222
1
k
CBA
T
=
γ−λ
γ−λ
=
λ
λ
λγ−λ
λ
=
Если М(s)=1, то
.
1
0
0
0
,
0
0
0
1
,
100
010
001
000
,
4
3
2
1
4
3444
2333
1222
111
==
λ
λ
λ
λ
=
=
+λ=
+λ=
+λ=
+λ=
T
CBA
xy
xxx
xxx
xxx
uxx
&
&
&
&
3.5.5. Метод аналогового моделирования
Метод основан на использовании приемов аналогового моделирования,
когда математическая модель системы, заданная дифференциальными уравне-
ниями, реализуется с помощью обратных связей на суммирующих, инверти-
рующих и интегрирующих типовых звеньях. Уравнения состояния записыва-
ются в этом случае в соответствии со схемой аналогового моделирования без
предварительного разложения передаточной функции на множители.
55
Пример. Дано дифференциальное уравнение системы, записанное в опе-
раторной форме (s
3
+a
1
s
2
+a
2
s+a
3
)y=(b
0
s
2
+b
1
s+b
2
)u.
Требуется получить уравнения состояния.
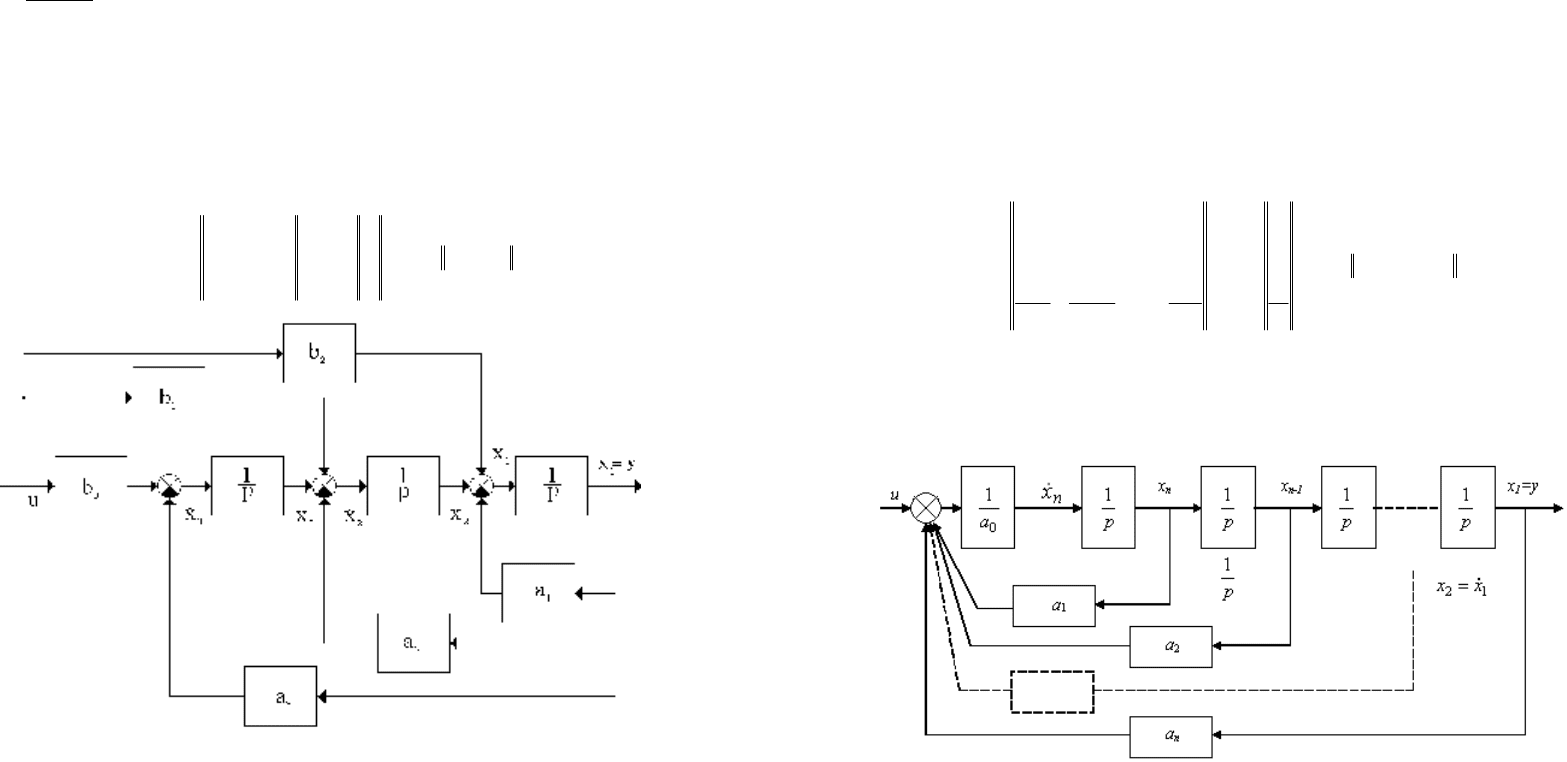
Решение: в соответствии с заданным дифференциальным уравнением со-
ставляем схему аналогового моделирования (рисунок 3.18), на основании ко-
торой уравнения состояния запишутся в виде
,;;;
101331123221121
xyubxaxubxaxxubxaxx =+−=+−=+−=
&&&
т.е.
.001,,
00
10
01
0
1
2
3
2
1
==
−
−
−
= C
b
b
b
B
a
a
a
A
Рисунок 3.18. Схема аналогового моделирования
3.5.6. Нормальная форма записи уравнений состояния
Под нормальной формой записи уравнений состояния подразумевается
тот случай, когда в качестве координат состояния принимаются выходная пе-
ременная и (n-1) её производных. Преимущества нормальной формы заключа-
ются в простоте представления исходных дифференциальных уравнений даже
тогда, когда они являются нелинейными или нестационарными. Например, для
системы второго порядка изменение состояния может быть представлено с
56
помощью фазового портрета на фазовой плоскости, а при n>2 выходная пере-
менная отображается траекториями в n – мерном фазовом пространстве. Очень
удобно применять нормальную форму записи уравнений состояния для мно-
гомерных систем с несколькими входами и выходами. Итак, задаваясь при
∑
=
−
=
n
i
n
i
papD
0
1
)(
в качестве координат состояния
123121
,,,,
−
====
nn
xxxxxxyx
&
L
&&
, получаем
.001,
1
0
0
,
000
010
0
0
1
0
1
0
L
M
L
LLLL
L
L
==
−−−
=
−
C
a
B
a
a
a
a
a
a
A
nn
(3.41)
Структурная схема аналогового моделирования объекта (системы), урав-
нение состояния которого записано в нормальной форме, представлена на ри-
сунке 3.19.
Рисунок 3.19. Схема моделирования системы с нормальной формой
Можно представить бесконечное множество систем с матричной матема-
тической моделью общего вида, которые будут между собой эквивалентны,
так как отличаются друг от друга только выбором базиса пространства состоя-
ний.

57
4. Расчет основных характеристик процессов и систем
4.1. Дисперсия стохастического процесса через вычеты
Вычисление дисперсии процесса g(t) и затем среднеквадратического от-
клонения производится при нахождении интеграла через вычеты [17]. Практи-
ческий пример для 4-й степени w спектральной плотности рассмотрен в [18].
Здесь рассмотрим более сложный пример для спектральной плотности (4.3).
Дисперсия процесса
.
125125
25625
2
1
28
2
∫
∞
∞−
++
+
= ω
π
d
ww
w
Dg
(4.1)
Используя факторизацию спектральной плотности, получим
∑
∫
=
∞
∞−
−
=
−
−
=
2/
1
)()(
)(
Res
)(
)(
)(
)(
2
1
n
k
k
j
j
g
sAsA
sC
ds
sA
sB
sA
sB
j
D
π
. (4.2)
Интеграл вычислим через вычеты по полюсам левой комплексной полу-
плоскости.
Вычеты в простых полюсах:
[ ]
−
−=
−
→
−
)()(
)(
)(lim)(Res
sAsA
sC
sssS
ik
ss
g
k
ik
. (4.3)
Вычеты в кратных (m-кратных) полюсах:
[ ]
−
−=
−
−
→
−
)()(
)(
)(lim)(Res
1
sAsA
sC
ss
ds
d
sS
m
ik
m
ss
g
k
ik
. (4.4)
4.2. Дисперсия стохастического процесса алгоритмом Острема
Острем разработал алгоритм расчета дисперсии стохастического процес-
са, заданного дробно-рациональной спектральной плотностью [19]. Соотно-
шение для расчета имеет вид
.
)()(
)()(
2
1
)(
2
1
1
∑
∫∫
=
∞
∞−
∞
∞−
=
−
−
π
=
π
=
n
k
k
j
j
j
j
Idw
sAsA
sBsB
j
dwwS
j
Dg
(4.5)
58
С учетом формулы вычисления каждого из интегралов имеем
=
β
2α
,
=
.
Для расчета примем
.,...,)(
;,...,)(
1
1
1
10
n
n
nn
n
n
n
nnnn
n
bsbsB
asasasA
+=
++=
−
−
(4.6)
Введем в рассмотрение полиномы для k-го шага
.,...,)(
;,...,)(
1
1
1
10
k
k
kk
k
k
k
kkkk
k
bsbsB
asasasA
+=
++=
−
−
Коэффициенты полиномов определяются рекуррентно из уравнений:
).(*)()(
);(*)()(
1
1
sAsBsB
sAsAsA
kkkk
kkkk
β−=
α
−
=
−
−
где
.2/)](*)1()([)(* sAsAsA
k
k
kk
−−−=
Коэффициенты
11
, , ,
−−
βα
k
i
k
ikk
ba
расчитываются по следующим формулам:
÷åòíî. åñëè ,-
íå÷åòíî, åñëè ,
íå÷åòíî; åñëè ,-
÷åòíî, åñëè ,
, ,
11
1
1
21
1
1
1
1
1
0
β
=
α
=
=β=α
++
+
−
++
+
−
iab
ib
b
iaa
ia
a
a
b
a
a
k
ik
k
i
k
i
k
i
k
ik
k
i
k
i
k
i
k
k
k
k
k
k
(4.7)
4.2.1. Реализация алгоритма Острема на основе Excel
Алгоритм Острема хорошо программируется как на языках высокого
уровня Pascal, C++, так и средствами программирования Excel.
Пример. Пусть спектральная плотность процесса имеет вид
59
.
0201,198,1
25,0
)(
24
2
++
+
=
ww
w
wS
g
Соответствующий формирущий фильтр
.
01,12
5,0
)(
2
++
+
=
ss
s
sW
g
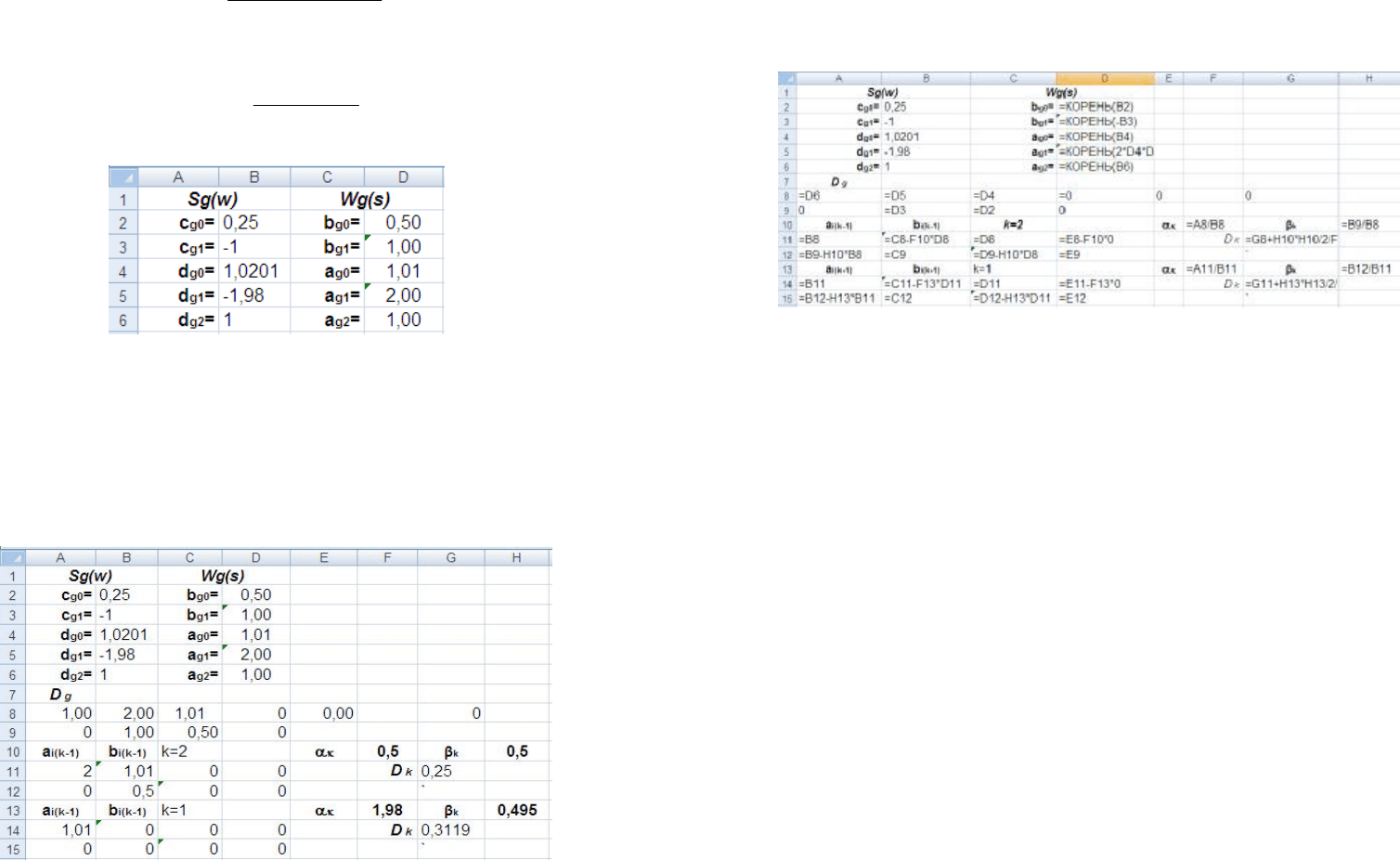
Так это выглядит в Excel:
Рисунок 4.1. Исходные данные для алгоритма Острема в Excel
Коэффициенты полиномов A
k
(s), B
k
(s) определяются рекуррентно из
уравнений (4.7). Исходные полиномы составлены на основе вычисленной пе-
редаточной функции Wg(s).
(
)
=
+
+
=
+2 +1,01,
(
)
=0+
+
= +0,5.
Расчет в электронной таблице (см. рисунок 4.2)
Рисунок 4.2. Реализация алгоритма Острема в Excel
60
В ячейках A8:C9 формируются полиномы A
2
(s) B
2
(s). Расчетные формулы
вводятся в ячейках A11:C12, для αk, βk в ячейках E10 и H10.
Скрин-копия с расшифровкой формул представлена на рисунке 4.3.
Рисунок 4.3. Реализация алгоритма Острема в Excel (продолжение)
Распространение формул на рекуррентный шаг k=1 производится путем
простого копирования строк 10, 12 в строки 13, 15.
Результаты вычисления дисперсии при использованиия прикладной про-
граммы Astrom.exe [19] в данном случае использованы для контроля правиль-
ности программы Excel. Исходные данные для решения задачи формируются в
файле S(w).dat и имеют следующий вид:
1 2 порядок системы
1 0,5 полином Bn(s)
1 2 1.01 полином An(s)
Результаты вычислений дисперсии при этом получены в файле Astr.dat.
k=2
1.00000 2.00000 1.01000
1.00000 0.50000
a[2]=0.50000 b[2]=0.50000
2.00000 1.01000
0.50000
D= 2.5000E-0001
a[1]=1.98020 b[1]=0.49505
1.01000
D= 3.1188E-0001
