Волков В.Л. Моделирование процессов и систем в приборостроении
Подождите немного. Документ загружается.

121
Говоря о «потоке событий», нужно иметь в виду, что здесь термин «со-
бытие» имеет значение, несколько отличное от того, к которому мы привыкли
в теории вероятностей. Там «событием» называется исход опыта, обладающий
вероятностью. События, образующие поток, сами по себе вероятностями не
обладают; вероятностями обладают другие, производные от них события, на-
пример, «на участке времени Δt произойдет событие».
Важной характеристикой потока событий является его интенсивность λ -
среднее число событий, приходящееся на единицу времени. Интенсивность
потока может быть как постоянной (λ =const), так и переменной, зависящей от
времени t. Например, поток отказов автомобиля в период обкатки имеет убы-
вающую интенсивность с течением времени.
Поток событий называется регулярным, если события следуют одно за
другим через определенные, равные промежутки времени. На практике чаще
встречаются потоки не регулярные, со случайными интервалами.
Поток событий называется стационарным, если его вероятностные харак-
теристики не зависят от времени. В частности, интенсивность λ стационарного
потока должна быть постоянной. Это отнюдь не значит, что фактическое чис-
ло событий, появляющихся в единицу времени постоянно. Поток неизбежно
(если только он не регулярный) имеет какие-то случайные сгущения и разре-
жения.
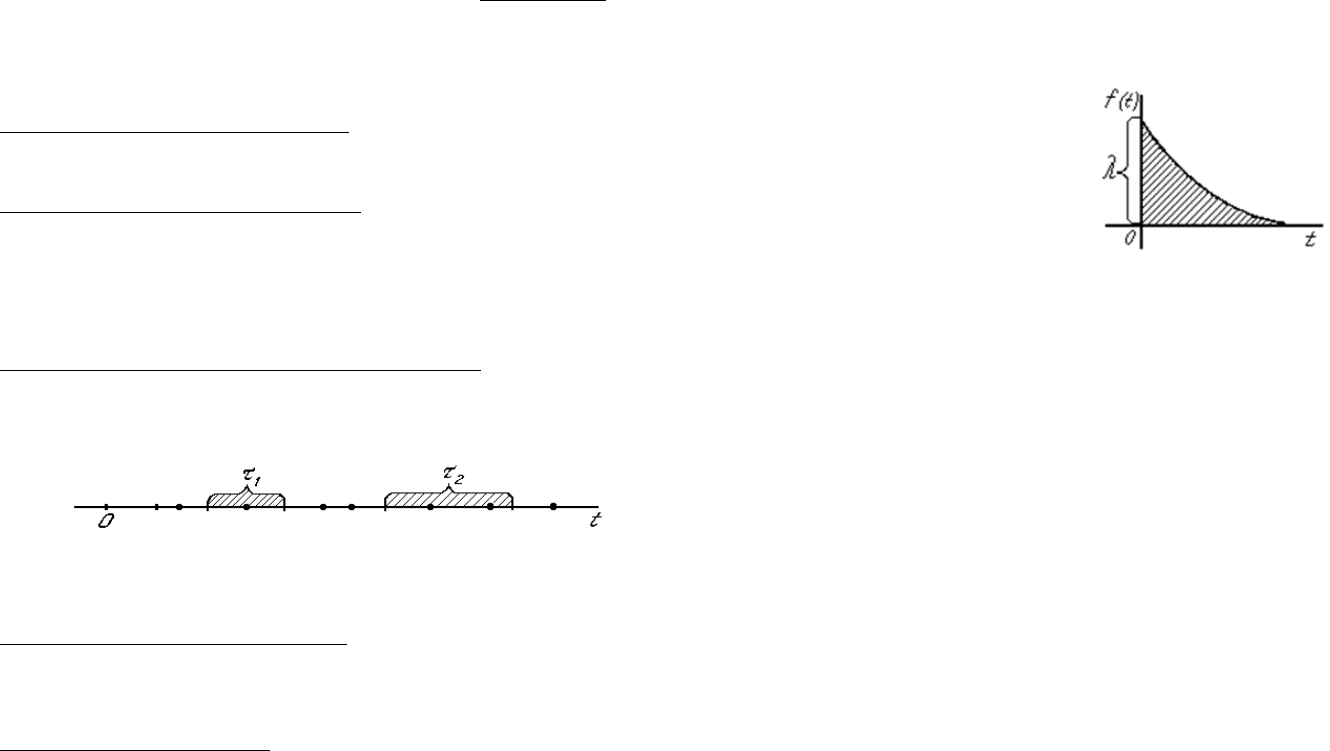
Поток событий называется потоком без последействия, если для любых
двух непересекающихся участков времени τ
1
и τ
2
(см. рис. 8.3) число событий,
попадающих на один из них, не зависит от того, сколько событий попало на
другой.
Рисунок 8.3. Возникновение событий без последействия
Если минимальный интервал между событиями много меньше среднего
интервала между ними t = 1/ λ, наличием последействия можно пренебречь.
Поток событий называется ординарным, если события в нем появляются
поодиночке, а не группами по нескольку раз. Если поток событий ординарен,
то вероятностью попадания на малый участок времени Δt двух или более со-
бытий можно пренебречь.
Пуассоновский поток событий. Поток событий называется простейшим
(или стационарным пуассоновским), если он обладает сразу тремя свойствами:
стационарен, ординарен и не имеет последействия. Название «простейший»
связано с тем, что процессы, связанные с простейшими потоками, имеют наи-
122
более простое математическое описание. Регулярный поток не является «про-
стейшим», так как обладает последействием.
Простейший поток играет среди других потоков особую роль, в чем-то
подобную роли нормального закона среди других законов распределения. А
именно, при наложении (суперпозиции) достаточно большого числа независи-
мых, стационарных и ординарных потоков (сравнимых между собой по интен-
сивности) получается поток, близкий к простейшему.
Для простейшего потока с интенсивностью λ интервал Т между соседни-
ми событиями имеет так называемое показательное распределение с плотно-
стью f(t) = λe
–λt
(см. рис. 8.4).
Рисунок 8.4. Показательное распределение простейшего потока событий
Величина λ в формуле (8.1) называется параметром показательного зако-
на. Для случайной величины Т, имеющей показательное распределение, мате-
матическое ожидание т
Т
есть величина, обратная интенсивности, а среднее
квадратическое отклонение σ
T
равно математическому ожиданию:
т
Т
= σ
T
=1/λ. (8.1)
В теории вероятностей в качестве «меры случайности» не отрицательной
случайной величины нередко рассматривают так называемый коэффициент
вариации:
V
T
= σ
T
/ т
Т
. (8.2)
Из формул (8.1), (8.2) следует, что для показательного закона распреде-
ления V
T
=1, т. е. для простейшего потока событий коэффициент вариации ин-
тервалов между событиями равен единице. Очевидно, что для регулярного
потока событий, у которого интервал между событиями не случаен (σ
T
= 0),
коэффициент вариации равен пулю. Для большинства потоков событий, встре-
чающихся на практике, коэффициент вариации интервалов между событиями
заключен между нулем и единицей и может служить мерой «степени регуляр-
ности» потока: чем V
T
ближе к нулю, тем «регулярнее» поток. Простейший
поток - это «наименее регулярный» из встречающихся на практике потоков.
123
В расчетах, связанных с потоками событий, удобно пользоваться поняти-
ем «элемента вероятности». Рассмотрим на оси Ot простейший поток с интен-
сивностью λ и произвольно расположенный элементарный участок времени Δt.
Элементом вероятности называется вероятность попадания на этот участок
хотя бы одного события потока. Легко доказать, что элемент вероятности (с
точностью до малых величин более высокого порядка по сравнению с Δt) ра-
вен
р
Δt
= λ Δt, (8.3)
т. е. для простейшего потока элемент вероятности равен интенсивности
потока, умноженной на длину элементарного участка.
Поток событий называется рекуррентным (иначе – потоком Пальма), ес-
ли он стационарен, ординарен, а интервалы времени между событиями T
1
, T
2
,
Т
3
,... представляют собой независимые случайные величины с одинаковым
произвольным распределением (например, с распределением, показанным на
рис. 8.5). Например, технический элемент − интегральная схема работает не-
прерывно до своего отказа, отказавший элемент мгновенно заменяется новым.
Если отдельные экземпляры элемента выходят из строя независимо друг от
друга, то поток отказов (он же «поток замен» или «восстановлении») будет
рекуррентным.
Очевидно, простейший поток представляет собой частный случай рекур-
рентного потока, когда интервалы между событиями имеют показательное
распределение. Другим частным (вырожденным) случаем рекуррентного по-
тока является регулярный поток событий, где интервалы вообще не случайны,
постоянны.
Рисунок 8.5. Пример потока Пальма
8.2. Уравнения Колмогорова для вероятностей состояний систем
Рассматривая Марковские процессы с дискретными состояниями и не-
прерывным временем, удобно представлять, что все переходы системы S из
состояния в состояние происходят под действием каких-то потоков событий
(поток вызовов, поток отказов, поток восстановлении и т.д.). Причем все по-
токи событий, переводящие систему S из одного состояния в другое про-
стейшие (простейший поток не обладает последействием).
124
Если система S находится в каком-то состоянии S
i
, из которого есть непо-
средственный переход в другое состояние S
j
(стрелка, ведущая из S
i
в S
j
на
графе состояний), то это будем представлять так, как будто на систему, пока
она находится в состоянии S
i
, действует простейший поток событий, перево-
дящий ее по стрелке из S
i
в S
j
. Как только появится первое событие этого пото-
ка, происходит «перескок» системы из S
i
в S
j
.
Для наглядности на графе состояний у каждой стрелки проставляется ин-
тенсивность потока событий, переводящего систему по данной стрелке. Обо-
значим λ
ij
интенсивность потока событий, переводящего систему из состояния
S
i
в S
j
.
Колмогоров доказал, что процесс P
i
(t) детерминирован и определяется
дифференциальными уравнениями Колмогорова.
Пусть марковский процесс находиться в состоянии S
i
– процесс может
выйти и войти в него. Для вычисления вероятностей состояний составляются и
решаются так называемые уравнения Колмогорова - особого вида дифферен-
циальные уравнения, в которых неизвестными функциями являются вероятно-
сти состояний. Вероятность сохранения i-го состояния за период Δt определя-
ется в виде:
=
=λ+λ−=
∆
−∆+
=
λ+λ−=
∆
−∆+
λ∆+λ∆−=∆+
∑
∑ ∑
∑ ∑
∑ ∑
=
= =
→∆
= =
= =
1)(
..1,)()()()(
)(
)()(
lim
)(
)()()()(
1
)]()([
)()())(1)(()(
1
1 1
0
1 1
1 1
N
i
i
N
j
N
j
ijjiji
i
ii
t
i
N
j
N
j
ijjijiii
N
j
N
j
jijjiii
tP
nittPttP
dt
tdP
t
tPttP
dt
tdP
ttPttP
t
tPttP
ttPttttPttP
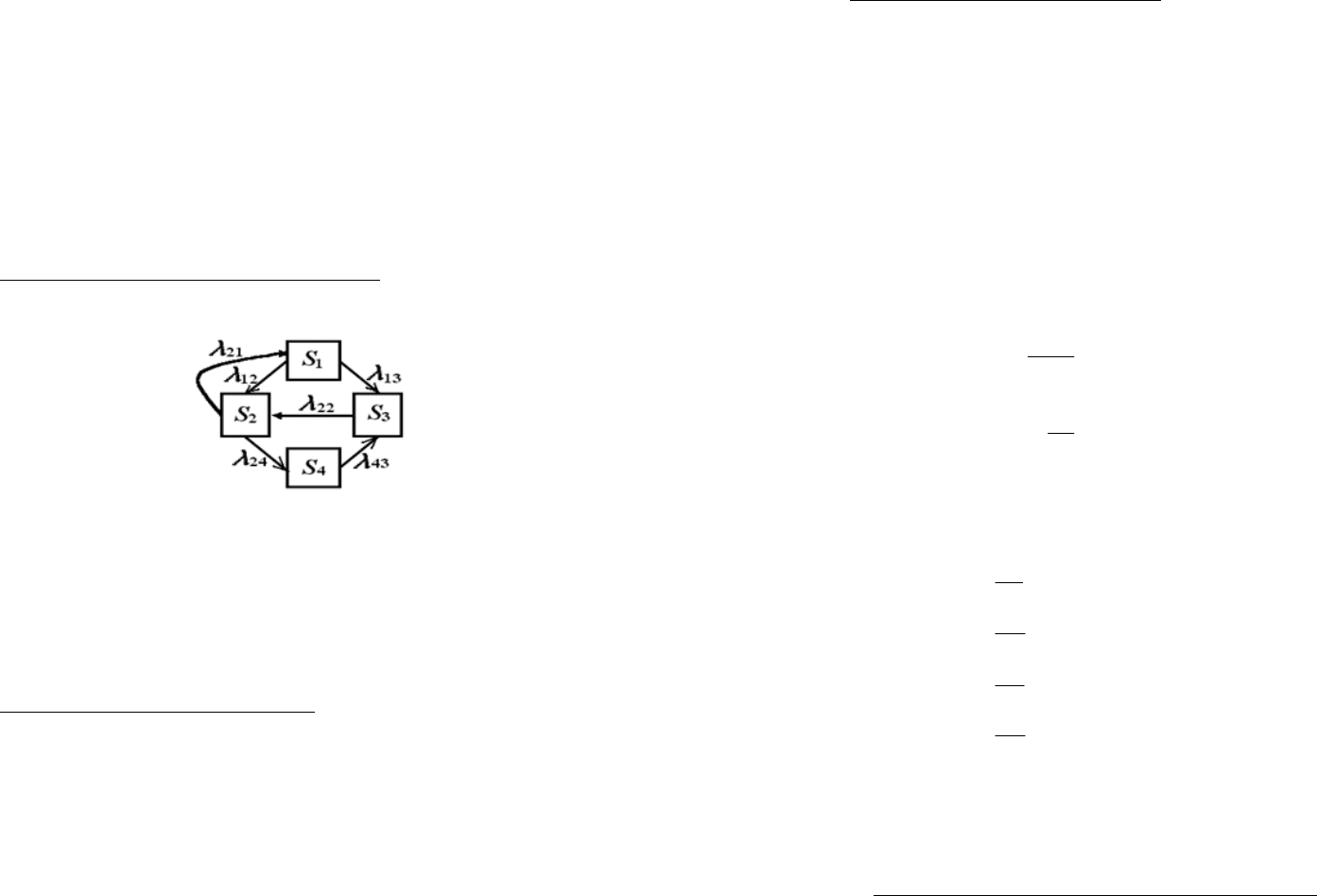
Пример. Пусть система (рисунок 8.6) находится в состоянии S
0
. Какой
поток событий переводит ее в состояние S
1
? Очевидно, поток отказов первого
узла. Его интенсивность λ
1
равна единице, деленной на среднее время безот-
казной работы первого узла. Какой поток событий переводит систему обратно
из S
1
в S
0
? Очевидно, поток «окончаний ремонтов» первого узла. Его интен-
сивность µ
1
равна единице, деленной на среднее время ремонта первого узла.
Аналогично вычисляются интенсивности потоков событий, переводящих сис-
тему по всем стрелкам графа.
125
Имея в своем распоряжении размеченный граф состояний системы, легко
построить математическую модель данного процесса. Пусть рассматривается
система S, имеющая n возможных состояний S
1
, S
2
, S
3
, …, S
n
. Назовем вероят-
ностью i-го состояния вероятность p
i
(t) того, что в момент t система будет на-
ходиться в состоянии S
i
. Очевидно, что для любого момента сумма всех веро-
ятностей состояний равна единице:
∑
=
=
n
i
i
tp
1
1)(
. (8.4)
Имея размеченный граф состояний, можно найти все вероятности со-
стояний p
i
(t) как функции времени.
Пример составления уравнений Колмогорова. Рассмотрим более слож-
ную систему S, которая имеет четыре состояния: S
1
, S
2
, S
3
, S
4
, размеченный
граф которых показан на рис.8.6.
Рисунок 8.6. Марковская система с четырьмя состояниями
Рассмотрим одну из вероятностей состояний, например p
1
(t). Это-
вероятность того, что в момент t система будет в состоянии S
1
. Придадим t
малое приращение ∆t и найдем p
1
(t+∆t) − вероятность того, что в момент t+∆t
система будет в состоянии S
1
. Это может произойти двумя способами: либо в
момент t система уже была в состоянии S
1
, а за время ∆t не вышло из него; ли-
бо в момент t система была в состоянии S
2
, а за время ∆t перешла из него в S
1
.
Найдем вероятность первого варианта. Вероятность того, что в момент t
система была в состоянии S
1
, равна p
1
(t). Эту вероятность нужно умножить на
вероятность того, что, находившись в момент t в состоянии S
1
, система за вре-
мя ∆t не перейдет из него ни в S
2
, ни в S
3
. Суммарный поток событий, выводя-
щий систему S
1
, тоже будет простейшим, с интенсивностью λ
12
+λ
13
(при нало-
жении двух простейших потоков получается опять простейший поток).
Значит вероятность того, что за время ∆t система выйдет из состояния S
1
равна (λ
12
+λ
13
)∆t вероятность того, что не выйдет: 1-(λ
12
+λ
13
)∆t. Отсюда веро-
ятность первого варианта равна p
1
(t)[1-(λ
12
+λ
13
)∆t].
126
Найдем вероятность второго варианта. Она равна вероятности того, что в
момент t система будет в состоянии S
2
, а за время ∆t перейдет из него в со-
стояние S
1,
т. е. она равна p
2
(t)λ
21
∆t.
Складывая вероятности обеих вариантов (по правилу сложения вероятно-
стей независимых событий) получим:
p
1
(t+∆t)=p
1
(t)[1-(λ
12
+λ
13
)∆t]+p
2
(t)λ
21
∆t. (8.5)
Раскроем квадратные скобки перенесем p
1
(t) в левую часть и разделим
обе части на ∆t:
(p
1
(t+∆t)-p
1
(t))/∆t=λ
21
p
2
(t)-(λ
12
+λ
13
)p
1
(t).
Устремим, как полагается в подобных случаях, ∆t к нулю слева получим
в пределе производную функции p
1
(t). Таким образом, запишем дифференци-
альное уравнение для p
1
(t):
)()()(
)(
11312221
1
tptp
dt
tdp
λ+λ−λ=
или короче:
11312221
1
)( pp
dt
dp
λ+λ−λ=
(8.6)
Рассуждая аналогично для всех остальных состояний, напишем еще три
дифференциальных уравнения. Присоединяя к ним уравнение (8.6) получим
систему дифференциальных уравнений для вероятностей состояний:
.
)(
)(
443224
4
332443131
3
22124332112
2
11312221
1
λ+λ=
λ−λ+λ=
λ+λ−λ+λ=
λ+λ−λ=
pp
dt
dp
ppp
dt
dp
ppp
dt
dp
pp
dt
dp
(8.7)
Это система четырех линейных дифференциальных уравнений с четырь-
мя неизвестными функциями p
1,
p
2
, p
3
, p
4
. Еще к этому можно добавить
p
1
+p
2
+p
3
+p
4
=1, можно также выразить любую из вероятностей p
i
через другие,
а соответствующее уравнение с производной (dp
i
)/dt отбросить.
Общее правило составления уравнений Колмогорова. В левой части
каждого уравнения системы стоит производная вероятности i-го состояния. В

127
правой части – сумма произведений вероятности всех состояний, из которых
идут стрелки в данное состояние на интенсивности соответствующих потоков
событий минус суммарная интенсивность всех потоков выводящих систему из
данного состояния умноженная на вероятность данного (i-го) состояния.
Пользуясь этим правилом, запишем уравнения Колмогорова для сис-
темы S, размеченный граф состояний которого дан на рис. 8.2:
(8.8)
Чтобы решить уравнения Колмогорова и найти вероятности состоя-
ний, надо задать начальные условия. Если известно начальное состояние сис-
темы S
i
, то в начальный момент (при t=0) p
i
(0)=1 а все остальные начальные
вероятности равны нулю. Так, например, уравнения (8.8) естественно решать
при начальных условиях p
0
(0)=1, p
1
(0)=p
2
(0)=p
3
(0) (в начальный момент оба
узла исправны).
Линейные дифференциальные уравнения с постоянными коэффициен-
тами можно решать аналитически, но это удобно только тогда когда число
уравнений не превосходит двух - трех. Если уравнений больше обычно их ре-
шают численно на ЭВМ. Уравнения Колмогорова дают возможность найти
все вероятности состояний как функции времени.
Финальные вероятности состояний. При t, стремящемся к бесконечности,
в системе устанавливается стационарный режим, при котором система случай-
ным образом меняет свои состояния, но их вероятности уже не зависят от
времени. Пределы вероятностей состояний при t стремящемся к бесконечности
называются финальными вероятностями состояний. Финальная вероятность
состояния S
i
− это среднее относительное время пребывания системы в этом
состоянии.
В теории случайных процессов доказано, что если число n состояний
системы конечно и из каждого из них можно (за конечное число шагов) перей-
ти в любое другое, то финальные вероятности существуют.
На рисунке 8.7 показан процесс установления финальных вероятно-
стей в стационарной системе.
.
)(
)(
)(
)(
3212102
3
2223102
2
1123201
1
0212211
0
µ+µ−λ+λ=
µ+λ−µ+λ=
µ+λ−µ+λ=
λ+λ−µ+µ=
ppp
dt
dp
ppp
dt
dp
ppp
dt
dp
ppp
dt
dp
128
P
i
t
P
i
=1
P
i
’
P
i
0
P
i’
*
(t)
P
i
, i
≠
i’
Рисунок 8.7. Процесс финализации вероятностей
Предположим, что условие существования финальных вероятностей вы-
полнено, тогда имеет место
.)(lim
ii
ptp =
(8.9)
Через некоторое время процесс успокаивается и вероятности станут кон-
стантами. Марковский процесс при t → ∞ вырождается в стационарный.
Финальные вероятности обозначаются теми же символами p
1
, p
2
, …, что
и вероятности состояний, имея ввиду постоянные числа. Очевидно, они тоже
образуют в сумме единицу (формула 8.4).
При t → ∞ в системе S устанавливается предельный стационарный ре-
жим, в ходе которого система случайным образом меняет свои состояния, но
их вероятности уже не зависят от времени. Финальную вероятность состояний
S
i
можно истолковать как среднее относительное время пребывания системы в
этом состоянии.
Вычисляются финальные вероятности из условия равенства нулю их
производных. Значит, чтобы найти финальные вероятности нужно все левые
части уравнений Колмогорова положить равными нулю и решить полученную
систему уже не дифференциальных, а линейных алгебраических уравнений.
Например, линейные алгебраические уравнения для финальных вероят-
ностей состояний системы, граф состояний которой дан на рис. 8.2, имеют вид
(8.10) .
)(
)(
)(
)(
2112321
3102221
321112
2211021
λ+λ=µ+µ
µ+λ=µ+λ
µ+λ=µ+λ
µ+µ=λ+λ
ppp
ppp
ppp
ppp
o
Для решения системы надо воспользоваться условием нормирования:
p
0
+p
1
+p
2
+p
3
=1
129
8.3. Основные модели марковских систем
Для составления математической модели марковской системы надо запи-
сать уравнения состояния Колмогорова и найти выражения для финальных
вероятностей состояний. Граф состояний для основной схемы состояний пред-
ставлен на рисунке 8.8.
Рисунок 8.8. Граф состояний процесса гибели и размножения
Для данного графа имеем уравнения финальных вероятностей состояний
(8.11)
,
,
,
,
1,1,1
....
1,1,1
....
221112
110001
λ=λ
λ=λ
λ=λ
λ=λ
−−−
−−−
nnnnnn
kkkkkk
pp
pp
pp
pp
кроме того, надо учесть условие нормирования. Решая систему, из перво-
го уравнения выразим p
1
, через p
0
(8.12).
0
10
01
1
pp
λ
λ
=
Из второго, учитывая (2.14), получим
0
1021
0112
2
pp
λλ
λ
λ
=
.
И для любого k
0
10211,
0112,1
...
pp
kk
kk
k
λλλ
λ
λ
λ
=
−
−
...
.
Подставим эти выражения в условие нормирования
1
...
,...,1
10211,
0112,1
1021
0112
10
01
0
=
λλλ
λλλ
++
λλ
λλ
+
λ
λ
+
−
−
kk
kk
p
...
,
откуда получим выражение для p
0
(8.13) .
...
...
,...,1
1
10211,
0112,1
1021
0112
10
01
0
−
−
−
λλλ
λλλ
++
λλ
λλ
+
λ
λ
+=
kk
kk
p
130
8.3.1. Фомула Литла
Найдем взаимосвязь среднего времени пребывания заявки в системе и
среднего числа заявок в системе.
В стационарном режиме работы системы среднее число заявок посту-
пающих в систему равно среднему числу заявок покидающих систему (обслу-
женных). Оба потока имеют одну и ту же интенсивность.
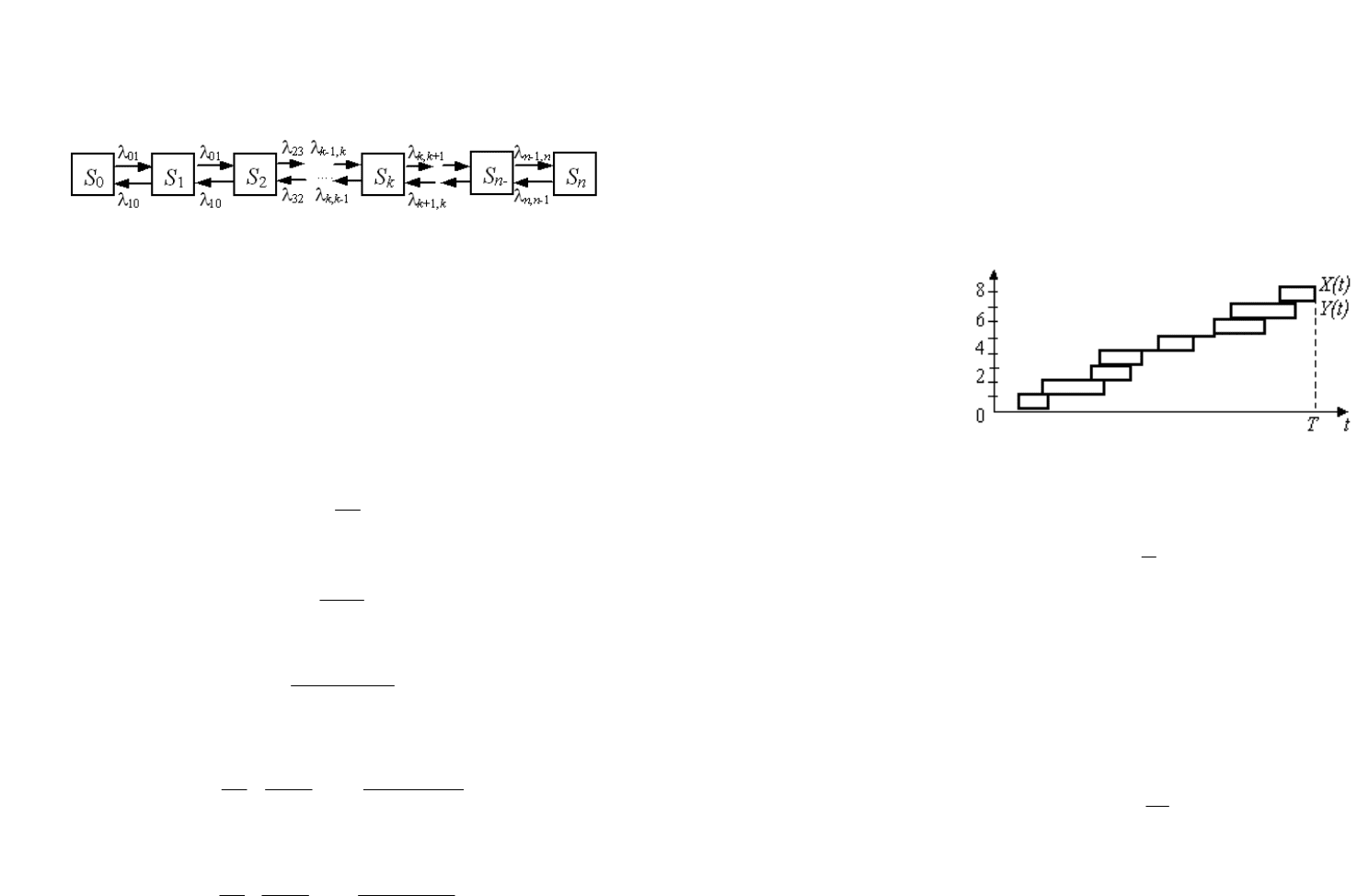
Обозначим: X(t) – число заявок поступивших до момента t, Y(t) – число
заявок покинувших систему до момента t. Разность Z(t)=X(t)-Y(t) – это число
заявок, находящихся в системе. Когда линии X(t) иY(t) сливаются, в системе
нет заявок (рис. 8.9).
Рисунок 8.9. Процесс поступления и обслуживания заявок
Среднее число заявок в системе равно интегралу от Z(t) деленному на
длину интервала T
∫
=
T
c
dttZ
T
Z
0
)(
1
.
Этот интеграл равен суммарной площади прямоугольников, изображен-
ных на рис.8.9. Прямоугольники имеют высоту, равную единице, а основание,
равное времени пребывания соответствующей заявки в системе (t
1
, t
2
,…). По-
лучим
∑
∫
=
i
i
T
tdttZ
0
)(
.
Запишем теперь Z
c
в виде
∑
λ
λ
=
i
ic
t
T
Z
1
,
где Tλ - среднее число заявок в системе за время T.
Среднее время пребывания заявки в системе равно отношению суммар-
ного времени заявок в системе к среднему числу заявок
131
(8.14) .
λ
=
∑
T
t
W
i
i
c
Учитывая (8.14), получим формулу Литтла для системы
cc
ZW
λ
=
1
, (8.15)
и для очереди
îî
1
ZW
λ
=
. (8.16)
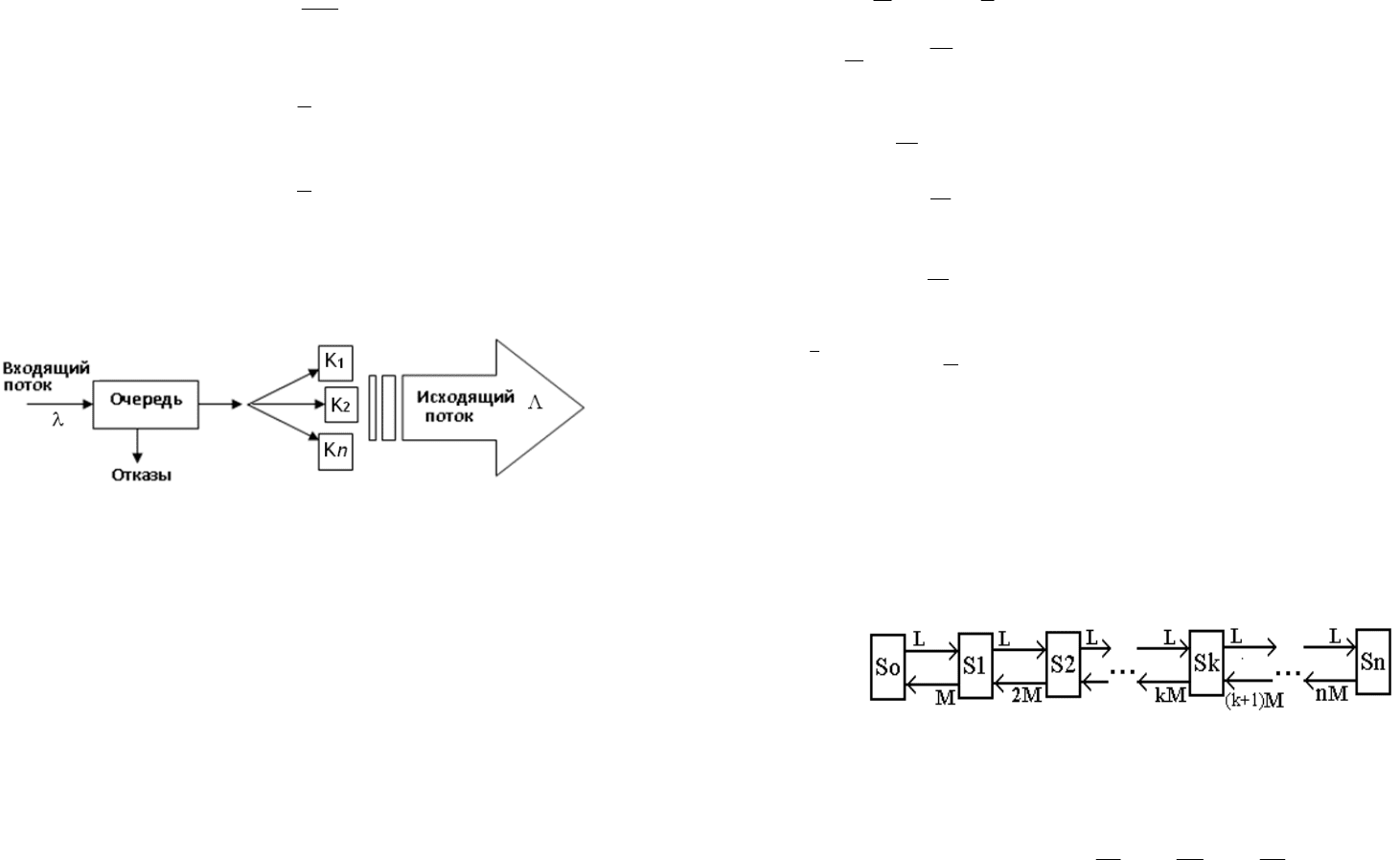
8.3.2. Функциональная схема многоканальной системы
Многоканальная однофазная марковская система может быть представ-
лена структурной схемой (рис. 8.10).
Рисунок 8.10. Схема многоканальной однофазной марковской системы
Основные характеристики системы: входящий поток – простейший с ин-
тенсивностью λ, n – каналов обслуживания, Λ< λ - часть заявок не обслужива-
ется, интервалы между событиями распределены экспоненциально f(t)= λe
-λτ
.
Информационные каналы статистически одинаковы и всегда исправны,
отказов в связи с поломкой нет. Время обслуживания каналом случайно, но у
всех приборов это время имеет плотность распределения f
0
(t)=µe
-µτ
(статисти-
чески независимо). Интервалы времени обслуживания заявок взаимонезависи-
мы.
Правила обслуживания:
• если все каналы заняты, заявка встает в очередь и ждет обслуживания;
• в модели безразлично в каком порядке будут обслужены заявки;
• освободившийся канал сразу приступает к обслуживанию заявки из очере-
ди, если таковая имеется;
• если величина очереди достигла (N-m) – предельной величины, очередная
заявка получает отказ.
132
Характеристики состояния:
µ
λ
=ρ
ρ
=
−
=
∑
ãäå ,
!
1
0
0
n
i
i
i
P
− вероятность того, что система будет простаивать,
niP
i
P
i
i
,1 ,
!
0
=⋅
ρ
=
− вероятность того, что в системе будет i-е число заявок.
Характеристики функционирования:
0îòê
!
P
n
PP
n
n
⋅
ρ
==
− вероятность отказа системы,
0îòê
!
11 P
n
PQ
n
ρ
−=−=
− относительная пропускная способность (вероятность -
заявка обслужена),
ρ
−λ=λ=
0
!
1 P
n
QA
n
− абсолютная пропускная способность (среднее число
заявок с системе),
∑
=
µ
=ρ==
n
i
i
A
Qipk
1
− среднее число занятых каналов.
8.3.3. Многоканальная система с отказами обслуживания
Многоканальная система с отказами обслуживания соответствует клас-
сическая задаче теории массового обслуживания − задаче Эрланга. Пусть име-
ется n-канальная система, на которую поступают заявки с интенсивностью L;
поток обслуживаний имеет интенсивность M, обратную среднему времени
обслуживания заявки t
o
. Обозначим p=L/M − приведенную интенсивность по-
тока заявок. Граф состояний системы представлен на рисунке 8.11.
Рисунок 8.11. Многоканальная система без очереди
Характеристики эффективности данной системы следующие:
p0, p1,...,pk - вероятности состояний системы (при p<1):
p p
p p
k
p
n
k n
0 1
2
2
1
= + + + + + +
−
!
,...,
!
,...,
!
,
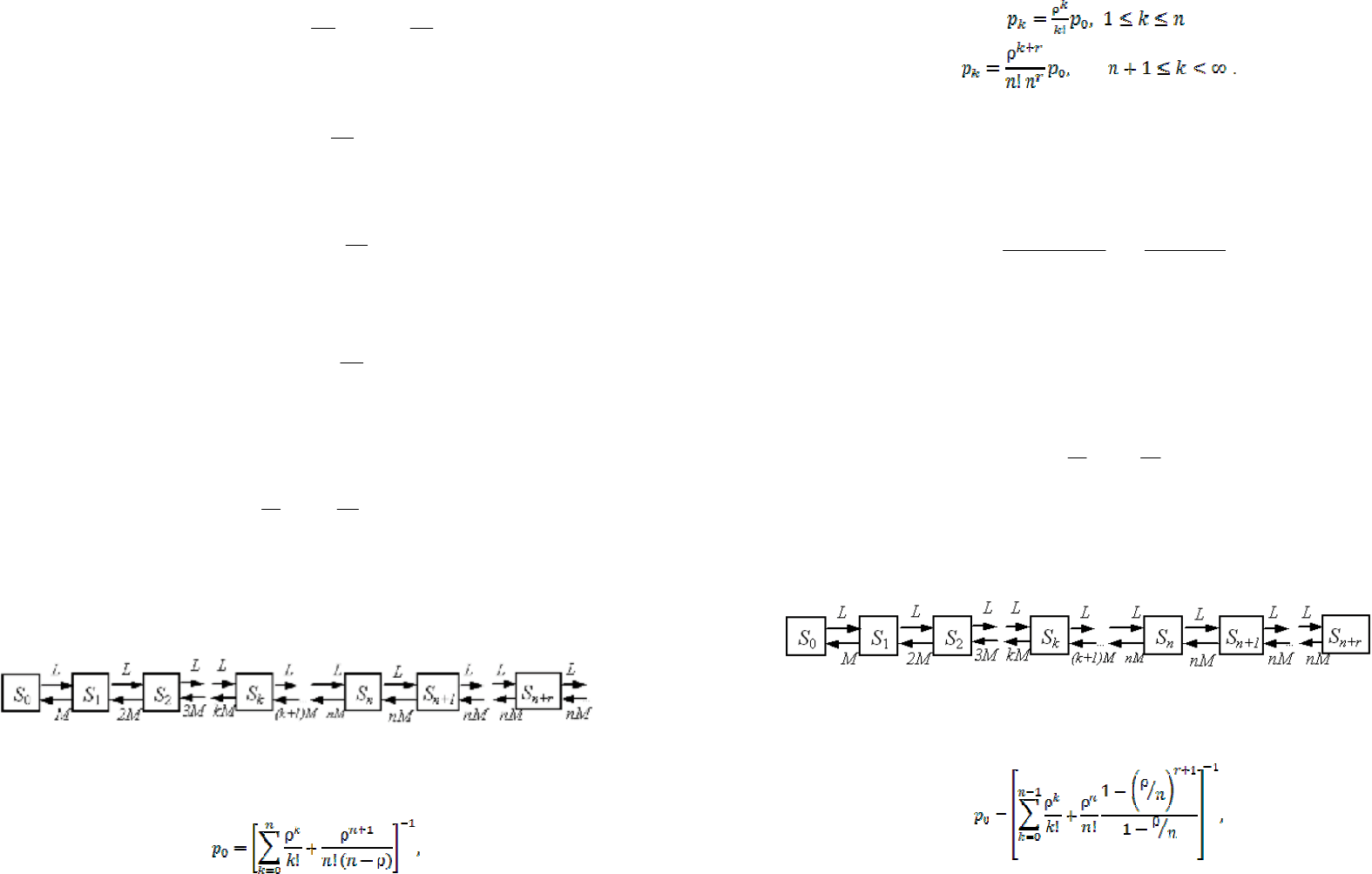
133
p pp pk
p
k
p pn
p
n
p
k n
1 0 0 0= = =,...,
!
,
!
;
p0 - вероятность того, что поступившая заявка получит отказ (все каналы заня-
ты):
Po pn
p
n
p
n
= =
!
;0
Q - относительная пропускная способность системы - вероятность того, что
заявка будет обслужена:
Q Po
p
n
p
n
=− =−1 1 0
!
;
А - абсолютная пропускная способность системы получается при умножении
интенсивности потока заявок L на Q:
A=LQ L
p
n
p
n
= −
1 0
!
;
k - среднее число занятых каналов равно математическому ожиданию дискрет-
ной случайной величины с возможными значениями 0,1,..., n и вероятностями
этих значений p0, p1,...,pn:
k=
A
M
p
p
n
p
n
= 1 0−
!
.
8.3.4. Многоканальная система с неограниченной очередью
Граф состояний системы изображен на рисунке 8.12.
Рисунок 8.12. Многоканальная система с неограниченной очередью
Характеристики данной системы следующие:
p
0
, p
1
,...,p
k
- вероятности состояний ИС (при ρ<1):
134
,
Zo - среднее число заявок в очереди:
∑
∞
=
+
==
1
][
r
rn
rprMZo
.
Выполняя преобразования (с дифференцированием ряда) получим
22
0
1
)/1()/1(! nn
p
nnn
p
Zo
n
n
ρ−
ρ
=
ρ−⋅
ρ
=
+
.
Zс - среднее число заявок в системе:
С учетом среднего числа заявок, находящихся под обслуживанием (сред-
него числа занятых каналов), получим
ρ
+
=
Zo
Zc
.
Wc, Wo - среднее время пребывания заявки в системе (очереди).
По формуле Литтла:
,
L
Zc
Wc =
L
Zo
Wo =
.
8.3.5. Многоканальная система с ограниченной очередью
Граф состояний системы изображен на рисунке 8.13.
Рисунок 8.13. Многоканальная система с ограниченной очередью
p
0
, p
1
,...,p
k
- вероятности состояний ИС (при ρ<1):

135
,
где ρ=L/M - среднее число заявок, поступающих в систему за время обслужи-
вания одной заявки,
r – максимальная длина очереди.
Z
о
- средняя длина очереди:
.
где k - текущее число заявок в очереди.
Вероятность того, что очередная заявка получит отказ, равна вероятно-
сти, что в системе уже находится n+r заявок
.
Среднее время ожидания в очереди связано со средней длиной очереди
îî
1
ZW
λ
=
.
Z
обсл
- среднее число занятых каналов (среднее число заявок, находящихся под
обслуживанием)
Wc - среднее время пребывания заявки в системе.
По формуле Литтла
.cc LZW =
136
8.3.6. Одноканальная система с неограниченной очередью
Пусть имеется одноканальная система с очередью, на которую не нало-
жено никаких ограничений (ни по длине очереди, ни по времени ожидания).
На эту система поступает простейший поток заявок с интенсивностью L; поток
обслуживаний имеет интенсивность M, обратную среднему времени обслужи-
вания заявки to. Обозначим p=L/M - приведенная интенсивность потока зая-
вок. Граф состояний системы изображен на рисунке 8.14.
Рисунок 8.14. Одноканальная система с неограниченной очередью
Характеристики эффективности данной система следующие:
p0, p1,...,pk - вероятности состояний система (при p<1):
p p p p p pk p p
k
0 1 1 1 1=− = − = −, ( ), ( );
Z
c
- среднее число заявок в системе:
;
1
][
0
c
p
p
kpkMZ
k
k
−
===
∑
∞
=
W
c
- среднее время пребывания заявки в системе по формуле Литтла:
;
)1(
1
c
pL
W
−
=
Z
о
- среднее число заявок в очереди: Z
о
=Z
c
-Z
oб
, где Z
c
- среднее число заявок в
системе; Z
oб
- среднее число заявок под обслуживанием. Число заявок под об-
служиванием в данной системе может быть либо нулем (если канал свободен),
либо единицей (если канал занят). Математическое ожидание (среднее значе-
ние Z
oб
) равно вероятности P
з
того, что канал занят (степень загрузки канала).
Очевидно, что P
з
=1-p0=p, где p0 - вероятность того, что канал свободен. Сле-
довательно, среднее число заявок под обслуживанием Z
oб
=p, отсюда имеем
Z
o
=Z
c
-Z
oб
=p/(1-p)-p=p
2
/(1-p);
W
о
- среднее время пребывания заявки в очереди по формуле Литтла:
;
)1(
2
o
pL
p
W
−
=
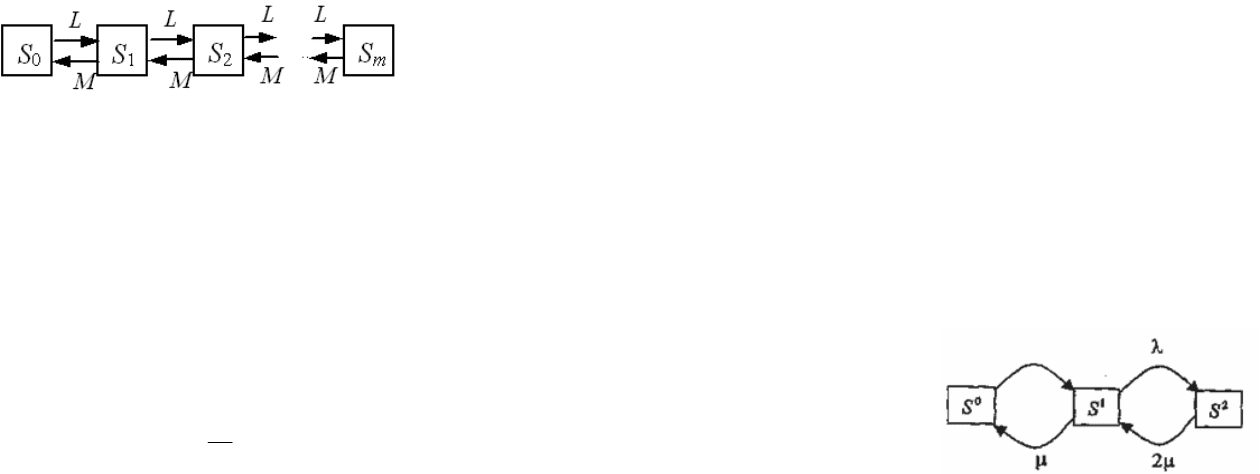
137
А - абсолютная пропускная способность системы: А=L, так как очередь
не ограничена и каждая заявка рано или поздно будет обслужена;
Q - относительная пропускная способность системы: Q=1 также ввиду
того, что очередь не ограничена и каждая заявка будет обслужена.
8.3.7. Одноканальная система с ограниченной очередью
Пусть имеется одноканальная система с очередью, которая не может пре-
вышать некоторого заданного числа m. На эту систему поступает простейший
поток заявок с интенсивностью L; поток обслуживаний имеет интенсивность
M, обратную среднему времени обслуживания заявки to. Обозначим ρ=L/M -
приведенная интенсивность потока заявок. Граф состояний системы изобра-
жен на рисунке 8.15.
Рисунок 8.15. Одноканальная система с ограниченной очередью
Характеристики данной системы следующие:
p
0
, p
1
,...,p
k
- вероятности состояний системы (при любом p):
Учитывая формулу (2.15) получим выражение для расчета p
0
(
)
1
2
0
...1
−
ρ+ρ+ρ+=
m
p
,
001
,..., pppp
m
m
ρ=ρ=
.
Z
c
- среднее число заявок в системе:
∑
=
ρ==
m
k
k
kkMZ
0
c
][
.
W
c
- среднее время пребывания заявки в системе по формуле Литтла:
L
Z
W
c
c
=
.
8.3.8. Одноканальная замкнутая система с m источниками заявок
Интенсивность потока заявок каждого клиента равна L, если заявка по-
ступила в момент, когда канал занят, то она ставится в очередь. Интенсивность
потока заявок для всего канала равна kL, где k=m-k
0
− число заявок, находя-
щихся в очереди и под обслуживанием.
138
Перечислим состояния системы:
S
0
– нет заявок в системе (интенсивность потока заявок mL),
S
1
– одна заявка в системе (обслуживается), очереди нет (интенсивность
потока заявок (m-1)L),
S
2
– две заявки в системе (одна обслуживается, одна в очереди), интенсив-
ность потока заявок равна (m-2)L,
. . .
S
m-1
– m-1 заявок в системе (одна обслуживается, m-2 в очереди), интенсив-
ность потока заявок равна L.,
S
m
– m заявок в системе (одна обслуживается, m-1 в очереди), интенсив-
ность потока заявок равна нулю.
(
)
1
0
...)1(1
−
ρ+ρ−+ρ+= mmp
,
0,,...,
0101
=ρ=ρ=
− mm
ppppmp
.
8.4. Уравнения состояния резервированной системы в динамике
Теперь рассмотрим случай резервированной системы, состоящей из двух
одинаковых блоков - основного и резервного при работе в динамическом ре-
жиме. Интенсивность отказов блока обозначим λ, а интенсивность его восста-
новлений - µ. Очевидно, что система может находиться в одном из трех со-
стояний:
S° − в системе исправны оба элемента;
S
1
− в системе работает один элемент, второй элемент отказал и восста-
навливается;
S
2
− в системе отказали оба элемента, которые восстанавливаются.
Граф состояний системы представлен на рисунке 8.16.
Рисунок 8.16. Граф состояний резервированной системы
Дифференциальные уравнения Колмогорова для вероятностей p
0
(t), p
1
(t)
и p
2
(t) состояний S
0
, S
1
и S
2
, в соответствии с рассмотренной ранее методикой,
получены в виде:

139
Подставляя p
2
(t) = 1 – p
0
(t) – p
1
(t) во второе уравнение, получаем
µ
+
µ
+
λ
−
µ
−
λ
=
2)()3()()(2)(
101
tptptp
&
.
Выразив p
1
(t) из первого уравнения системы и вычислив на основе полу-
ченного выражения
)(
1
tp
&
, подставим p
1
(t) и
)(
1
tp
&
в последнее уравнение. В
результате получаем линейное неоднородное дифференциальное уравнение
второго порядка
2
0
2
00
μ2)()μλ(2)()μλ(3)( =++++ tptptp
&&&
.
Характеристический многочлен соответствующего однородного уравне-
ния имеет вид
0)(2)(3
22
=µ+λ+µ+λ+
rr
.
Отсюда по известной формуле могут быть получены два вещественных
корня
)(
1
µ
+
λ
−
=
r
и r
2
=-2
)
(
µ
+
λ
, и решение однородного уравнения может
быть записано в виде
tt
eCeCtp
)(2
2
)(
10,0
)(
µ+λ−µ+λ−
+=
.
Из этого решения методом вариации постоянных может быть получено
частное решение неоднородного уравнения, а затем и общее решение
tt
eCeCtp
)(2
2
)(
1
2
2
0
)(
)(
µ+λ−µ+λ−
++
µ+λ
µ
=
.
Подставляя полученное выражение для p
0
(t) и производную
)(
0
tp
&
в пер-
вое уравнение системы, получаем выражение для p
1
(t)
tt
eCeCtp
)(2
2
)(
1
2
1
2
)(
2
)(
µ+λ−µ+λ−
+
µ
µ
+
λ
+
µ+λ
λµ
=
.
Произвольные постоянные могут быть определены из начальных условий
p
0
(0)=1 и p
1
(0)=0:
140
tt
eetp
)(2
2
2
)(
2
2
0
)3()(
)()3(
)3()(
2
)(
)(
µ+λ−µ+λ−
µ+λµ+λ
µ+λλ+µ+λλµ
+
µ+λµ+λ
λµ
+
µ+λ
µ
=
;
tt
eetp
)(2
2
2
)(
2
1
)3()(
)()3(2
)3(
2
)(
2
)(
µ+λ−µ+λ−
µ+λµ+λ
µ+λλ+µ+λλµ
+
µ+λ
λ
+
µ+λ
λµ
=
.
Сумма выражений для p
0
(t) и p
1
(t) определяет нестационарный коэффи-
циент готовности, а входящие в них постоянные слагаемые - стационарный
коэффициент готовности системы.
Здесь рассмотрен случай, когда избыточная система состоит из одинако-
вых элементов, что является частным случаем. Примером более сложной сис-
темы, для которой это условие не выполняется, может служить комплексная
ИИС, в состав которой входит несколько различных измерителей. Эти измери-
тели имеют различные интенсивности отказов, более сложную схему включе-
ния (например, по мажоритарному принципу). Граф состояний будет тоже бо-
лее сложный, но применяя, рассмотренные здесь стандартные методики, мож-
но рассчитать и оптимизировать важнейшие характеристики надежности ком-
плексной системы.
