Волков В.Л. Моделирование процессов и систем в приборостроении

Подождите немного. Документ загружается.

101

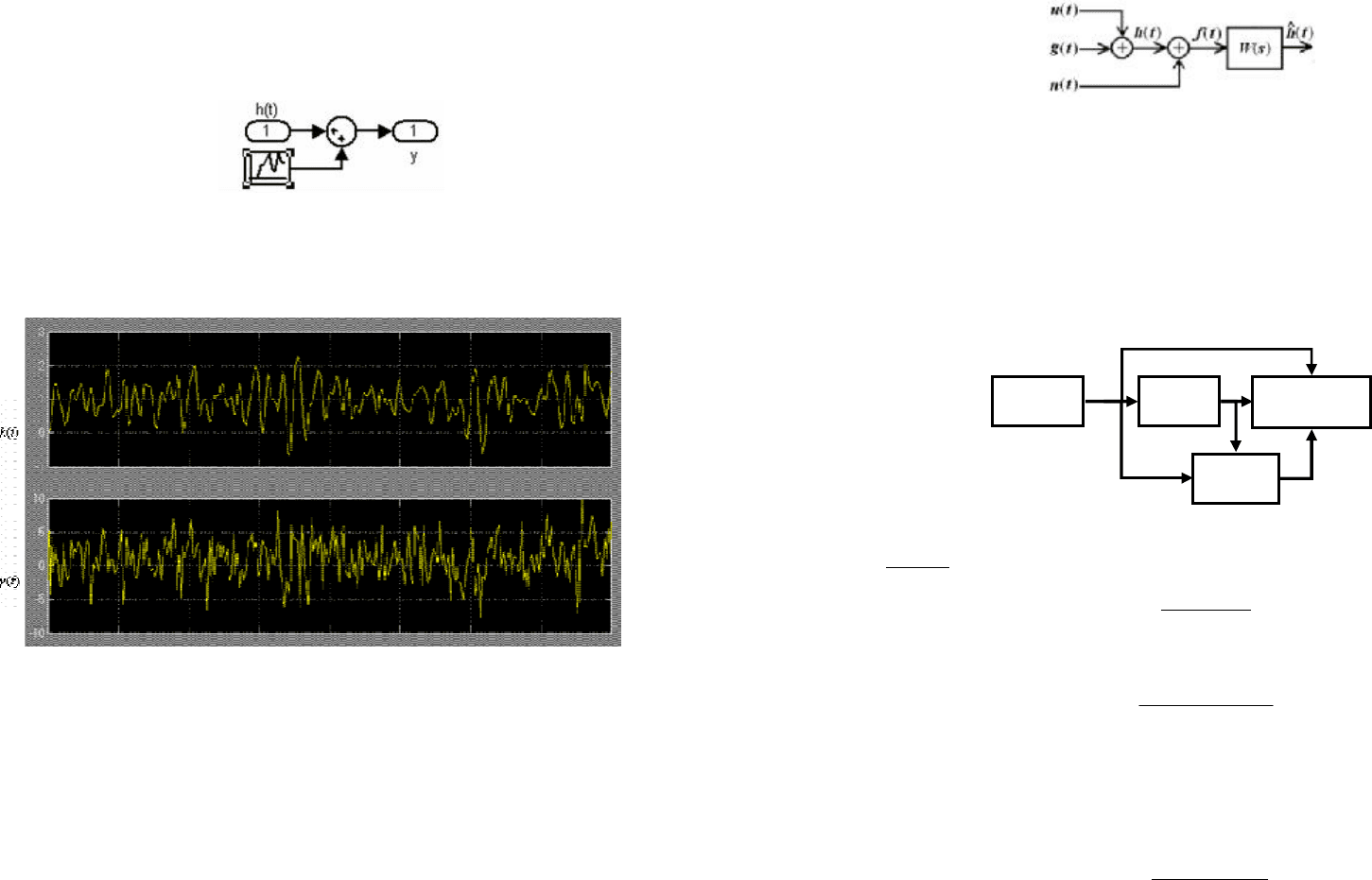
В соответствии со схемой формирования сигналов (рис. 1) измерение y(t)

является аддитивной смесью полезного сигнала h(t) и помехи n(t):

y(t)=h(t)+n(t). Такое формирование в реальных условиях осуществляет датчик

первичной информации ДПИ. Его модель представлена на рис.6.18.

Рисунок 6.18. Моделирование измерения y(t)

На осциллограммах рис. 6.19 представлены процессы h(t) и y(t), получен-

ные при моделировании процессов.

Рисунок 6.19. Осциллограммы процессов h(t) и y(t)

6.3.1. Моделирование непрерывной системы контроля

Система контроля предназначена для измерения и выдачи информации о

контролируемом процессе h(t), который содержит среднюю (детерминирован-

ную) составляющую и стохастическую (случайную) g(t). Измерение происхо-

дит при воздействии аддитивных шумов n(t). Датчик, с помощью которого

производятся измерения, является динамическим звеном (в данном случае

второго порядка). Эквивалентная схема системы контроля представлена на

рисунке 6.20.

102

Рисунок 6.20. Схема системы контроля

Случайная составляющая g(t) измеряемого процесса задана спектральной

плотностью Sg(w); детерминированная − сигналом u(t); h(t)=g(t)+u(t) − полный

информационный процесс; f(t)=h(t)+n(t) − измерение процесса h(t) с аддитив-

ными шумами n(t) (задана спектральная плотность шума − Sn(w)); h^(t) − вы-

ходной сигнал ДПИ; W(s) − передаточная функция ДПИ. Детерминированное

входное воздействие задано суммой ступенчатой и гармонической функций.

Для моделирования системы контроля в Matlab составляется схема моде-

ли рис. 6.21.

Рисунок 6.21. Схема моделирования системы контроля

Пример. Задана спектральная плотность контролируемого процесса

)(

+ω+ω

+ω

=wS

передаточная функция объекта наблюдения

28,018,02

45,0

)(

и интенсивность шумов измерений R=17 (при измерении выходного сиг-

нала объекта наблюдения).

Путем факторизации из модели в виде спектральной плотности получим

передаточную функцию формирующего фильтра входного процесса.

2236,2

)(

Матричная модель ОН находится методом вспомогательной перемен-

ной. Уравнение состояния в данном случае X'=A

X+B

u+D

v. Процесс h(t) на

(

)

F(t)

Сигналы Датчик

Блок

ошибок

(t)

Регистратор

103

выходе ОН вычисляется в матричном виде: g =C

X, где матрицы A

, D

, C

определяются по матричным соотношениям (формулы (3.6) [1]).

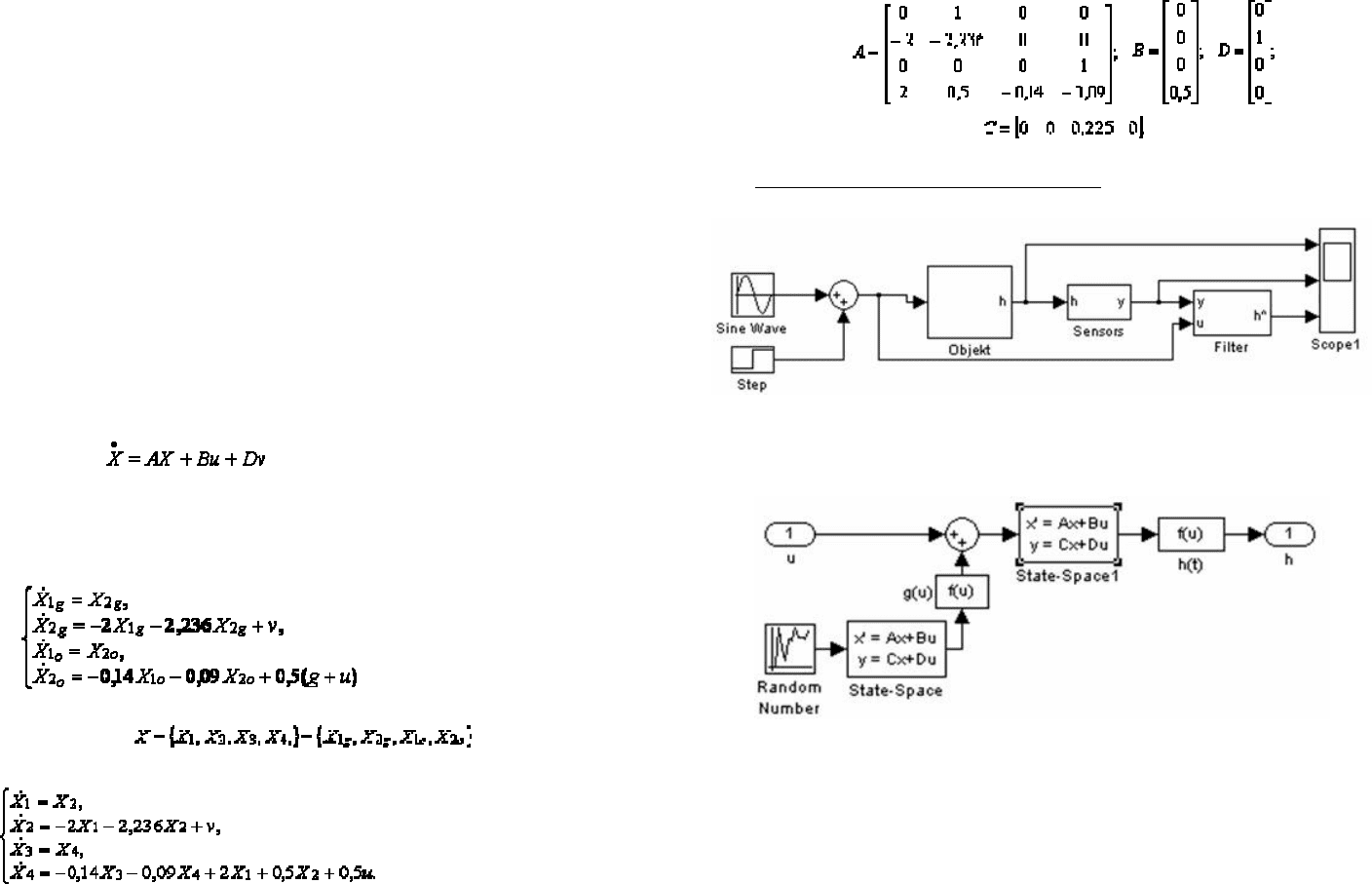
В данном примере получим следующий вид матриц

[ ]

. 14 ;

;

236,22

























−−

ggg

CBA

Матричная модель датчика

имеет вид

[ ]

. 025,0 ;

5,0

;

09,014,0

000

























−−

= CBA

Выход объекта наблюдения h =C

Полное уравнение объекта контроля содержит уравнение состояния

входного процесса и уравнение состояния объекта:

Здесь матрицы A, B, D составляются на основе дифференциальных урав-

нений процесса и объекта контроля, которые имеют вид

или относительно полного вектора

Матрицы A, B,C, D в этом случае имеют вид

104

Моделирование и исследование в MatLab. Cоставлена схема (рис. 6.22).

Рисунок 6.22. Схема верхнего уровня системы контроля в Matlab

Схема динамической системы, включающая стохастический процесс и

датчик, представлена на рис. 6.23.

Рисунок 6.23. Схема динамической системы

Настройка блока уравнения состояния представлена в окне параметров на

рис. 6.24.

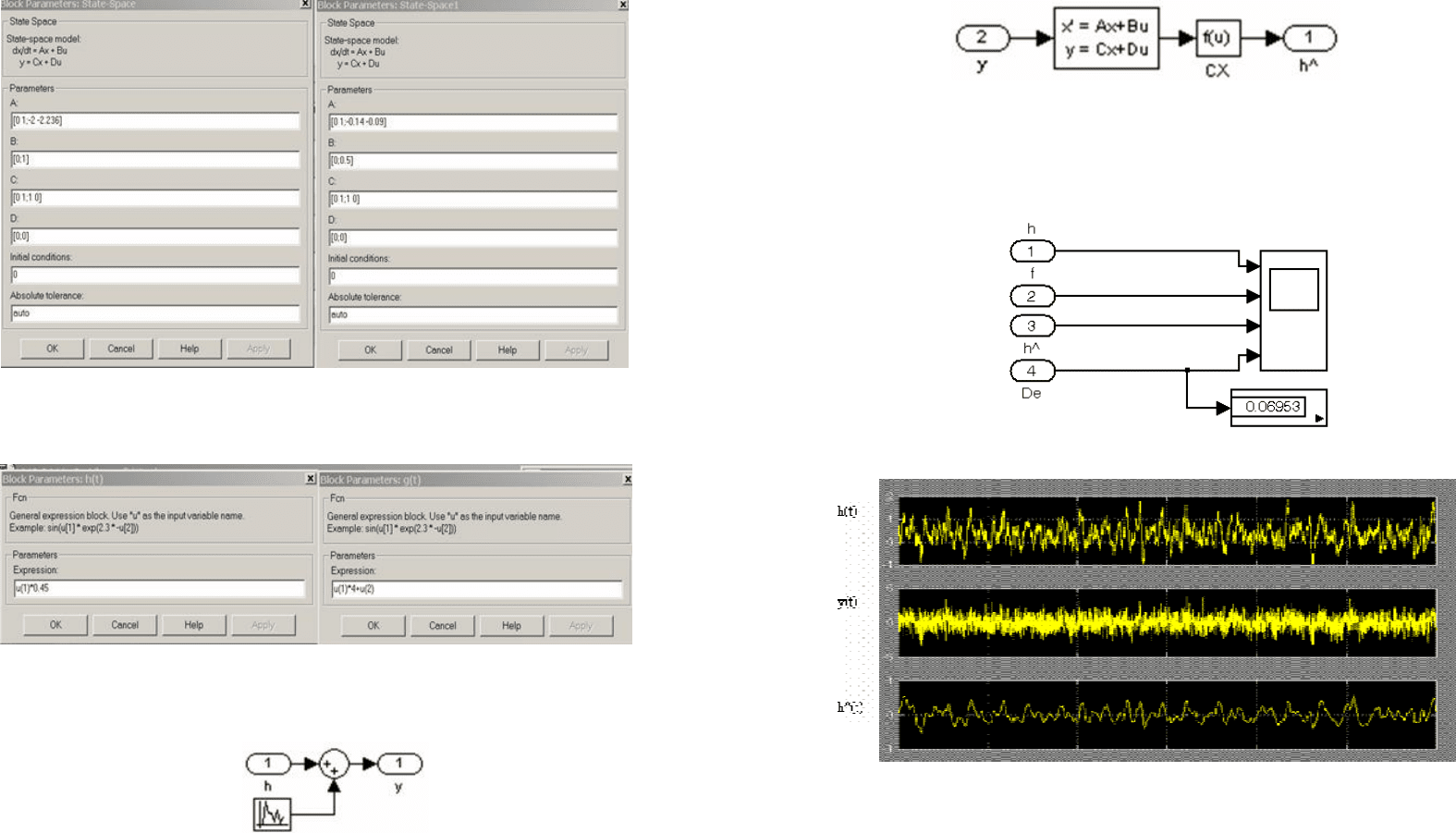
105

Рисунок 6.24. Окно настройки параметров

Функциональный блок, вычисляющий h(t)=CX, задан функцией пред-

ставленной в окне параметров рис. 6.25.

Рисунок 6.25. Настройка функциональных блоков

Сенсор (датчик) представлен схемой рис. 6.26. Интенсивность шума ге-

нератора белого шума составляет 0,4.

Рисунок 6.26. Модель сенсора

Блок Filter на основе измерений выдает оценку выходного параметра

объекта наблюдения – h^(t). Схема моделирования фильтра в данном случае

представлена на рис. 6.27.

106

Рисунок 6.27. Модель фильтра

Матрицы A, B, C соответствуют матрицам полной модели, матрица С в

блоке State Spase – единичная.

Результаты процессов системы представлены на рис. 6.29. На осцилло-

граф поданы сигналы согласно схеме рис. 6.22.

Рисунок 6.28. Регистратор процессов

Рисунок 6.29. Результирующие процессы

6.3.2. Моделирование дискретной системы контроля

Дискретная модель содержит неизвестные матрицы F, G. Расчет матриц

F, G выполняется итерационным алгоритмом в виде разложения в матричный

ряд Тейлора. Для этого используется вспомогательная матрица ψ:

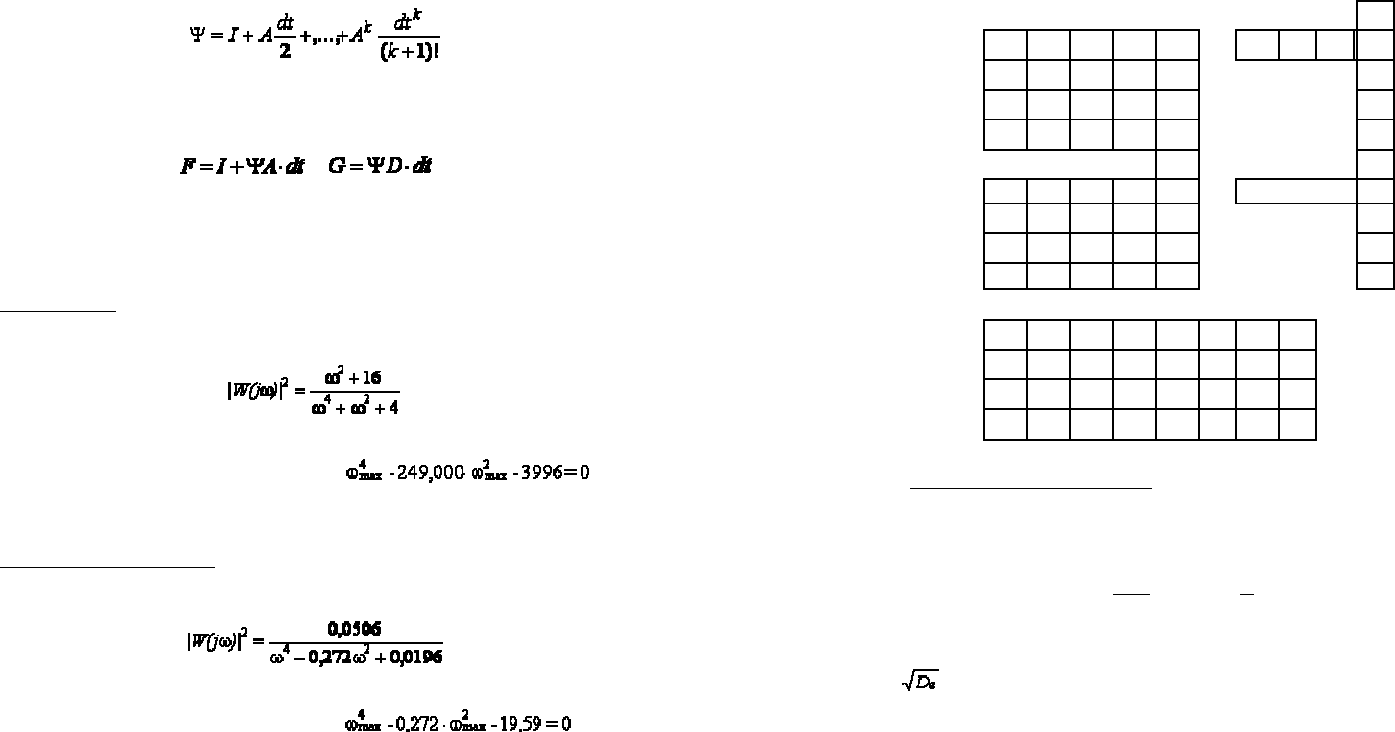
107

При этом матрицы F, G вычисляются по формулам:

, . (6.1)

Для расчета дискретной матричной модели определяется период дис-

кретности ОН в соответствии с импульсной теоремой [1]: dt=1/(2F

), где F

максимальная частота пропускания ОН.

Для процесса. Квадрат модуля амплитудно-фазочастотной характеристи-

ки (АФЧХ) процесса

Для расчета w

max

получим соотношение .

Получим w

max

=16,25 рад/с. В соответствии с импульсной теоремой [1,

с.12], период дискретности процесса: dt

=0,19 c.

Для объекта наблюдения. Квадрат модуля амплитудно-фазочастотной ха-

рактеристики (АФЧХ)

Для расчета w

max

получим соотношение .

Получим w

max

=2,136 рад/с. В соответствии с импульсной теоремой пери-

од дискретности объекта наблюдения определяется в виде dt

=π/w

max

=1,47 c.

Для реализации модели как процесса, так и объекта наблюдения выбира-

ется минимальный период дискретности dt

min

= dt

=0,19 c.

Матрицы F, G могут быть найдены с помощью электронных таблиц Ex-

cel при использовании формул (6.1).

108

A B C D

0,0000

1,0000

0,0000

0,4500

0,0000

2,0000

2,2360

0,0000

1,0000

0,0000

1,0000

0,0000

4,0000

1,0000

0,1400

0,0900

0,5000

0,0000

F G

C T

0,9687

0,1529

0,0000

0,1900

0,0000

0,4500

0,0157

0,3059

0,6

267

0,0000

0,1529

0,0693

0,0196

0,9975

0,1882

0,0090

0,0012

0,7136

0,2136

0,0264

0,9805

0,0941

0,0196

I Psi

1,0000

0,0000

0,9892

0,0824

0,0000

1,0000

0,0000

0,1648

0,8050

0,0000

1,0000

0,0000

0,0234

0,0064

0,9992

0,0944

0,0000

1,0000

0,3648

0,1034

0,0132

0,9907

Оценка дисперсии процесса. Экспериментальное исследование диспер-

сии процесса проводится на основе численной оценки дисперсии ошибки. Ре-

куррентная формула такой оценки имеет вид [9]:

.)]([

)1(

)(

+−

−

(6.2)

Среднеквадратическое отклонение в этом случае рассчитывается по фор-

муле , где D

установившееся значение дисперсии (=D

(n)).

Схема для вычисления D

представлена на рисунке 6.30.

Эта схема соответствует формуле (6.2). Для формирования векторного

сигнала, состоящего из компонент h(t), h^(t), D

(k-1), k использован блок Max

из библиотеки элементов Matlab Simulink (сигнал h^(t) задается равным нулю).

Затем этот вектор обрабатывается функциональным блоком f(u) - D

, в виде

(u(2)-u(1))*(u(2)-u(1))/(u(3))+u(4)*(u(3)-1)/(u(3)),

т.е. реализуется формула (6.2). Сигнал u(3) вырабатывается вторым функцио-

нальным блоком (=1+u[1]/0.1) и с учетом u[1]=i*dt (где i – номер дискретного

времени в диапазоне 0…400, dt=0,1 с – период дискретности) соответствует k.

109

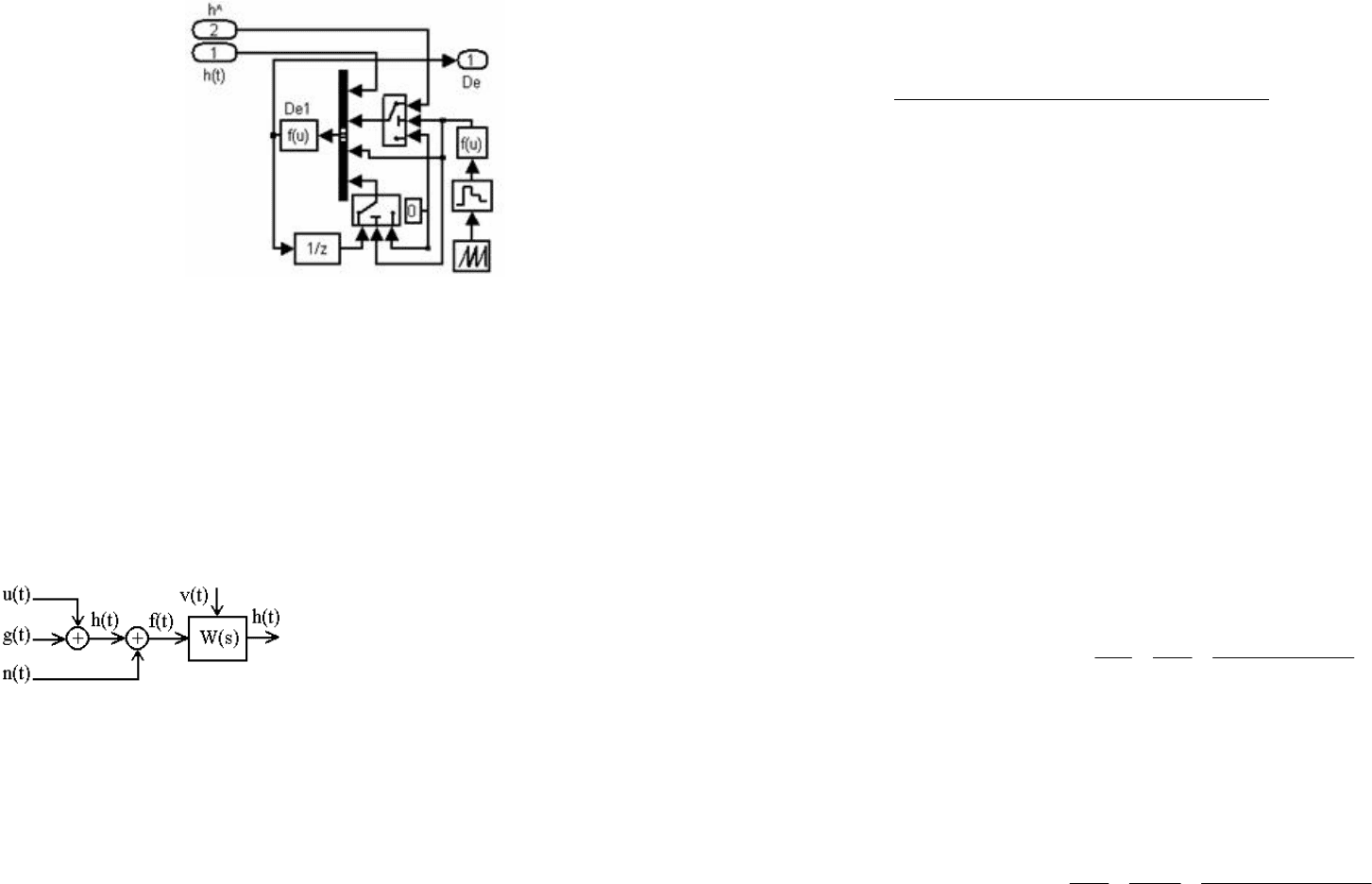
Рисунок 6.30. Схема вычисления дисперсии ошибки оценивания

Блок 1/z – предназначен для задержки на один такт сигнала D

(k) и полу-

чения на выходе D

(k-1).

Нижний переключатель управляется переменной k (номер дискретного

времени) и при начальном k=0 дает на выходе ноль. Если бы не делать такую

блокировку, то на вход блока Max проходил бы неопределенный сигнал с 1/z и

получился бы сбой в работе.

7. Примеры моделирования

7.1. Моделирование датчика при сигнале и аддитивном шуме

Структурная схема ДПИ с воздей-

ствующими сигналами представлена на

рис. 7.1. Случайная составляющая g(t)

измеряемого процесса задана спектраль-

ной плотностью Sg(w); детерминирован-

ная − сигналом u(t); h(t)=g(t)+u(t) − пол-

ный информационный процесс (ИП);

f(t)=h(t)+n(t) − измерение процесса h(t) с аддитивными шумами n(t) (задана

спектральная плотность шума − Sn(w)); v(t) − возмущающее воздействие на

ДПИ; h^(t) − выходной сигнал ДПИ; W(s) − передаточная функция ДПИ. На

практике встречается задача исследования ДПИ, измеряющего детерминиро-

ванно-стохастические физические величины в условиях внешних помех и при

наличии внутренних параметрических шумов, проявляющихся, например, в

мультипликативных и аддитивных изменениях статической характеристики

ДПИ [10]. Полная модель ДС в данном случае состоит из трех отдельных мо-

Рис.7.1. Структурная схема ДПИ

110

делей: 1) модели для полезной случайной составляющей Xg′=AgXg+DgVg; 2)

модели помехи X′n=AnXn+DnVn; 3) модели ДПИ, определяемой передаточ-

ной функцией W(s): Xw′=AwXw+Dwf(t).

Алгоритм формирования полной модели ДПИ.

1. Вычисление передаточных функций формирующих фильтров ИП g(t) и

помехи n(t).

2. Определение максимальных частот спектров ИП, шума и вычисление их

периодов дискретизации.

3. Определение полосы пропускания ДПИ, периода дискретизации для его

цифрового моделирования, результирующего периода дискретизации системы

ДПИ с сигналами.

4. Формирование моделей сигналов g(t), n(t), ДПИ и модели выхода в мат-

ричной непрерывной форме (для g(t) и n(t) - методом вспомогательной пере-

менной, для ДПИ - методом нормальной формы Коши).

5. Формирование дискретных матричных моделей сигналов и ДПИ.

6. Вычисление среднеквадратической ошибки на выходе ДПИ.

7. Моделирование процессов в ДПИ в дискретном времени и исследование

графиков и численной информации.

Модель случайных сигналов формируется из спектральных плотностей

Sg(w) и Sn(w) путем факторизации и определения передаточных функций фор-

мирующих фильтров Wg(s) и Wn(s) с последующим нахождением матричных

моделей в пространстве состояний методом вспомогательной переменной.

Модель в пространстве состояний методом вспомогательной переменной со-

ставляется на основе передаточной функции формирующего фильтра. Для

сигнала g(t)

...

)(

sdsdd

sbsbb

sWg

+++

===

Уравнениe состояния сигнала X'g=AgXg+DgVg. Сигнал на выходе фор-

мирующего фильтра g(t)=CXg. Матрицы Ag, Dg, Cg определяются методом

вспомогательной переменной.

Модель динамики ДПИ составляется на основе передаточной функции.

Выражение W(s) ДПИ имеет дробно-рациональный вид:

...

)(

wnww

wmww

sasaa

sbsbb

sAw

sBw

+++

===

111

Преобразование модели W(s) в матричную модель в данном случае осу-

ществляется в канонической нормальной форме Коши. Период дискретности

равен минимальному из значений для ДПИ и ИП.

Возникновение ошибок ДПИ связано с прохождением на выход шумов и

искажением полезного сигнала динамикой ДПИ. Теоретическое значение

среднеквадратической ошибки (СКО) находится через спектральную плот-

ность в соответствии с соотношением

∫

∞

)(

СКО dwwSe

, (7.1)

где спектральная плотность ошибки Se(w) вычисляется в виде

),()(1)()()(

wSgjwWwSnjwWwSe −+=

(7.2)

(W(jw) - амплитудно-фазочастотная характеристика ДПИ). Экспериментальное

значение СКО при моделировании на ПЭВМ вычисляется как среднее по всем

дискретным точкам наблюдения:

CKO = −

∑

yk gk

[() ()].

(7.3)

7.2. Моделирование процессов с заданными свойствами

Реальные ИИС и САУ работают с детерминированно-стохастическими

сигналами. В ИИС к ним относятся измеряемые физические величины, шумы

измерений, выходные сигналы, параметры вектора состояния. В САУ стохас-

тическими процессами являются возмущения объекта управления, сигналы,

измеряемые ДПИ, параметры вектора состояния. В связи с этим задача моде-

лирования процессов с заданными статистическими характеристиками (мате-

матическим ожиданием, спектральной плотностью, дисперсией) при исследо-

вании ИИС, САУ и просто ДПИ является актуальной.

Рассмотрим задачу моделирования класса эргодических процессов. Они

определяются математическим ожиданием и корреляционной функцией (или,

что эквивалентно, спектральной плотностью). Пусть для стохастического

112

процесса такого класса g(t) задано математическое ожидание Mg и дробно-

рациональная спектральная плотность Sg(w). Процесс g(t) задан спектральной

плотностью Sg(w). Детерминированная составляющая процесса u(t)=Mg

;

h(t)=g(t)+u(t) - полный ИП; y(t)=h(t)+n(t) - измерение процесса h(t) с аддитив-

ными шумами n(t) (задана интенсивность шума Sn(w)=R).

Информационный процесс g(k) представляется моделью в пространстве

состояний - векторной случайной последовательностью Х(k) (n-мерным векто-

ром состояния); v(k) - формирующий шум векторной случайной последова-

тельности X(k). При этом g(k)=СХ(k).

Алгоритм формирования модели.

1. На основе первичной модели ИП - S(w) находится динамическая модель

его формирующего фильтра.

2. На основе передаточной функции формирующего фильтра составляется

матричная непрерывная модель ИП (X'(t)=AX(t)+DV(t) - система дифференци-

альных уравнений первого порядка).

3. Вычисляется максимальная частота спектра ИП - Fm (полоса пропускания

формирующего фильтра).

4. По импульсной теореме определяется период дискретизации ИП.

5. Формируется результирующая дискретная матричная модель ИП

(X(k+1)=FX(k)+TV(k) - система разностных уравнений первого порядка).

6. Определяется уравнение формирования процесса g(k) в зависимости от

переменных вектора состояния X (g(k)=CX(k)).

Пример. Пусть детерминированно-стохастический ИП задан средним зна-

чением Mg=0,1 и спектральной плотностью

Sgw

() .=

+ +

2 8

198

10201

4 2

Шум измерения процесса характеризуется интенсивностью R=0,01. При

использовании CAD-MS в разделе MODEL задаем исходные данные, например,

по варианту 1, и определяем все последующие модели. Получим передаточ-

ную функцию формирующего фильтра

Wgs

()

, ,

+ +

14 28

101

Полоса пропускания фильтра составляет Wc=0,0139 рад/с, соответст-

вующий период дискретизации должен быть не более 0,1 с. В качестве резуль-

113

татов получим матричные модели в непрерывной форме: X'g=AgXg+DgVg,

g(t)=CgXg и в дискретной форме: Xg(k+1)=FgXg(k)+TgV(k), g(k)=CgXg(k), где

матрицы Ag, Dg, Cg, Fg, Tg соответственно равны:

[ ]

Ag Dg Cg=

























0 1

-101 -20

1,4, , , ,

Fg Tg=

























0978 000022,

0,0179

-1,81 0,62

0,018

Детерминированная составляющая процесса моделируется аналитиче-

скими выражениями (в данном случае скачкообразный сигнал).

Результаты. Исследуются числовые характеристики процесса: математи-

ческое ожидание, корреляционная функция, дисперсия, спектральная плот-

ность. Эти характеристики оцениваются методами математической статисти-

ки. Процесс и его статистические характеристики иллюстрируются на дисплее

и записываются в виде дискретных значений в файл на диске.

Для моделируемого процесса компоненты вектора состояния X(k) пред-

ставляются в виде графиков на экране дисплея в диалоговом режиме по рисун-

ку структурной схемы. В качестве результатов моделирования ИП на графиках

изображены: полный ИП h(t)=g(t)+n(t); измерение процесса с шумами f(t);

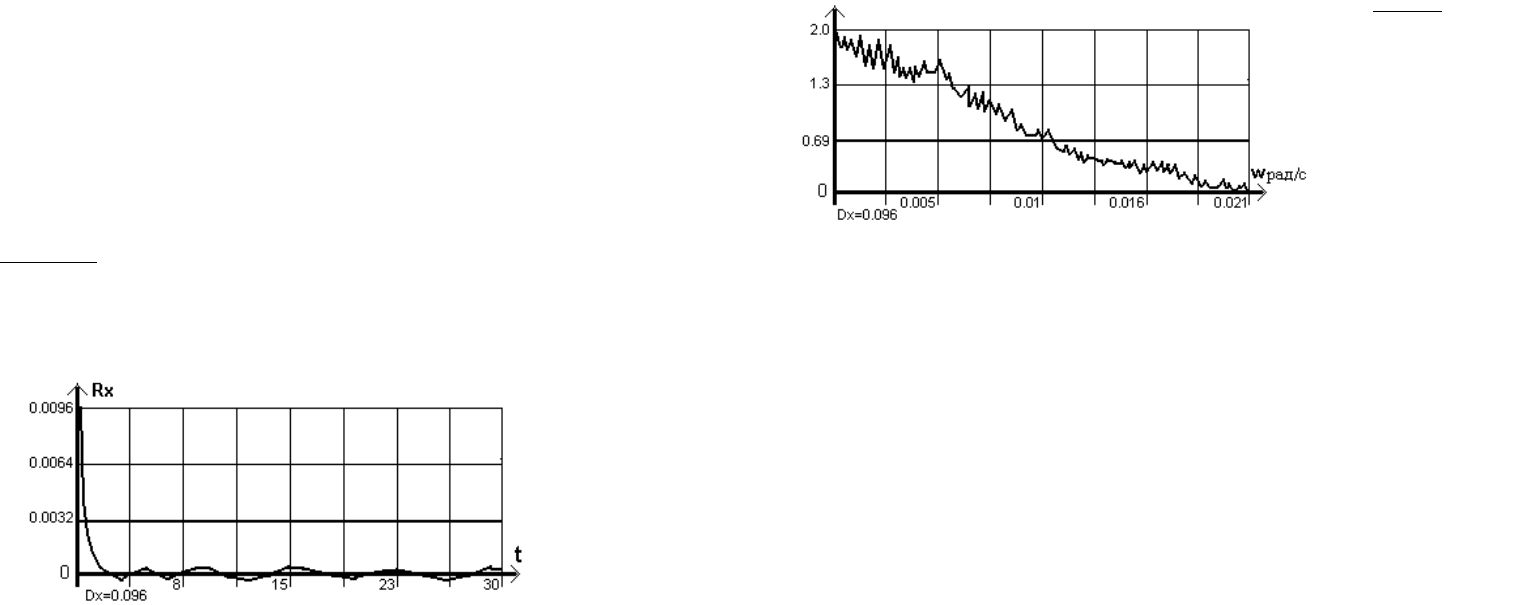
корреляционная функция Rg(r) (рис.7.2); спектральная плотность Sg(w)

(рис.7.3). График корреляционной функции может быть аппроксимирован

формулой Rx(τ)=σ

-ατ

, где σ

- дисперсия процесса g(t); α - постоянная кор-

реляции, которая вычисляется из графика на уровне 2 с. График спектральной

плотности показывает распределение мощности процесса по частотам. Эффек-

тивный диапазон частот процесса определяется круговой частотой, примерно

равной 0,01 рад/с, что соответствует теоретическому значению. Оценки дис-

Рисунок 7.2

114

персии процесса, вычисленные через корреляционную функцию и спектраль-

ную плотность, совпали и составляют 0,096.

Выводы. Матрич-

ная модель ИП являет-

ся универсальной и

удобна для цифрового

моделирования на

ПЭВМ. Исследование

процессов необходимо

во многих задачах ИИС

и САУ, например, для

ДПИ с воздействую-

щими сигналами и аддитивными шумами, для ДС с объектом управления при

воздействии возмущений и входных сигналов, для ИИС с детерминированны-

ми и стохастическими сигналами и несколькими ДПИ.

8. Марковские процессы и системы

Стохастические системы относятся к классу сложных систем. Состояния

таких систем рассматриваются с позиций случайных марковских процессов.

Пусть имеется некоторая физическая система S (в данном случае ИИС),

которая с течением времени меняет свое состояние, причем заранее неизвест-

ным, случайным образом.

Например S - техническое устройство, состоящее из ряда узлов, которые

время от времени выходят из строя, заменяются или восстанавливаются. Про-

цесс, протекающий в этой системе, безусловно, случаен.

Строго говоря, все процессы в природе случайны. До тех пор, пока слу-

чайные возмущения несущественны, мало влияют на интересующие парамет-

ры, можно ими пренебречь и рассматривать процесс как детерминированный,

неслучайный.

8.1. Марковские процессы

Марковским называется случайный процесс, протекающий в системе, ес-

ли для любого момента времени t

вероятностные характеристики процесса в

будущем зависят только от его состояния в данный момент t

и не зависят от

того, когда и как система пришла в это состояние [34].

Рисунок 7.3

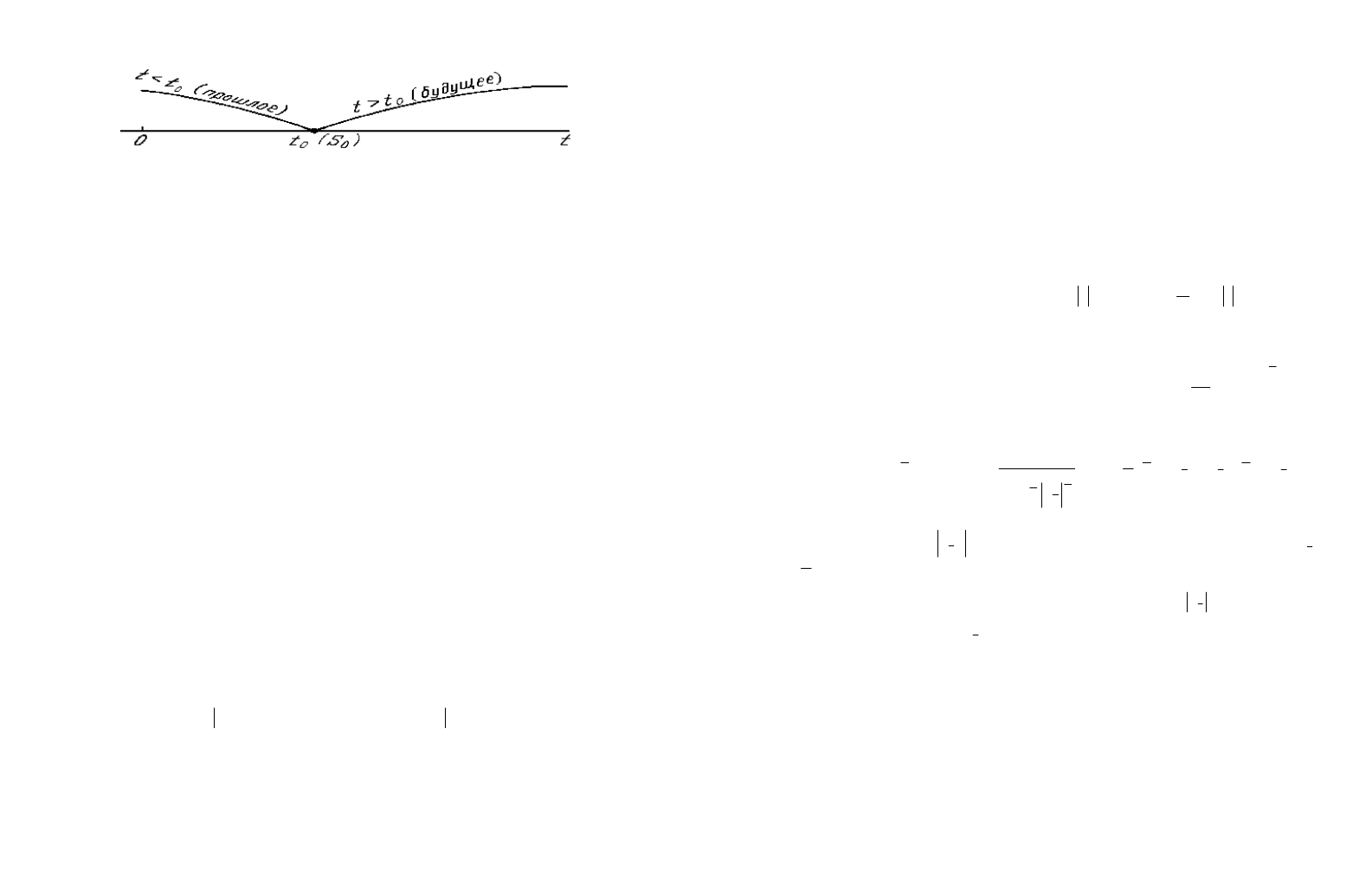
115

Это очень важное определение. Пусть в настоящий момент t

(см. рис.8.1)

система находится в определенном состоянии S

Рисунок 8.1. Связь будущего состояния системы с прошлым через настоящее

Естественно, интересует будущее состояние при t > t

. Можно ли его

предсказать? В точности - нет, т.к. процесс случайный. Но какие-то вероятно-

стные характеристики процесса в будущем можно найти. Например, вероят-

ность того, что через некоторое время t система S окажется в состоянии S

или

сохранит состояние S

, и т. п. Для марковского случайного процесса такое «ве-

роятностное предсказание» оказывается гораздо проще, чем для немарковско-

го. Если процесс - марковский, то предсказывать можно, только учитывая на-

стоящее состояние системы S

и забыв о его «предыстории» (поведении систе-

мы при t<t

). Само состояние S

, разумеется, зависит от прошлого, но как

только оно достигнуто, о прошлом можно забыть. Иначе формулируя, в мар-

ковском процессе «будущее зависит от прошлого только через настоящее».

На практике часто встречаются процессы, которые хотя и не марковские,

но могут быть в каком-то приближении рассмотрены как марковские. Практи-

чески любой процесс можно рассматривать как марковский, если все парамет-

ры из «прошлого», от которых зависит «будущее», включить в «настоящее».

В основе рассматривается непрерывный случайный процесс x(t), опреде-

ляемый заданием системы случайных величин x(t

), x(t

),..., x(t

), соответст-

вующих значениям случайного процесса в фиксированные моменты времени

, t

,…, t

. Эти случайные величины описываются n-мерной плотностью f (x

,…, x

, t

,...,t

) вероятности.

Основное свойство марковского процесса может быть выражено соотно-

шением для условной плотности при любых t

< t

<…<t

))()1(())(),...,(,)()1((

21 kkkk

txtxftxtxtxtxf +=+

Размерность n вектора x(t) называют порядком марковского процесса.

Марковская модель безусловно является определенной идеализацией по отно-

шению к реальным процессам, однако, несмотря это, она признается во многих

практических случаях достаточно адекватной. Достоинство этой модели со-

116

стоит в возможности использования эффективных алгоритмов обработки ин-

формации.

Корреляционная функция K

(τ), отражающая зависимость процесса во

времени (быстродействие), может с ростом τ или монотонно убывать или

стремиться к нулю по более сложному закону. Корреляционные функции,

наиболее часто имеющие место на практике, описываются выражениями:

|)|exp()(

τα−σ=τ

.cos|)|exp()(

βττα−σ=τ

Примерами корреляционных функций, соответствующих дифференци-

руемым процессам, могут служить:

);exp()(

222

τα−σ=τ













τβ

+τβ×τα−σ=τ sincos)exp()(

Наиболее часто также случайные процессы является гауссовскими (нор-

мальными) случайными процессами x(t), у которых для вектора

, образован-

ного совокупностью случайных величин x

= x(t

) (

nk ,1=

), все плотности рас-

пределения вероятности любого порядка имеют вид

( )













−−−

−

)()(

exp

)...,,,,(

21 xx

mxPmx

tttxf

где х=(x

, x

,...,x

)

1−

− определитель ковариационной матрицы

векто-

ра

Далее рассматриваются процессы, для которых

0≠

. Недиагональные

элементы p

матрицы

являются значениями взаимной корреляционной

функции х

и х

для моментов времени t

и t

. В случае стационарного гауссов-

ского процесса плотность зависит лишь от величин интервалов между рас-

сматриваемыми точками на оси времени.

Другим важным стационарным случайным процессом марковских систем

является процесс w(t) типа «белый шум», под которым понимается процесс с

нулевым математическим ожиданием и корреляционной функцией

)()(

где q - интенсивность белого шума;

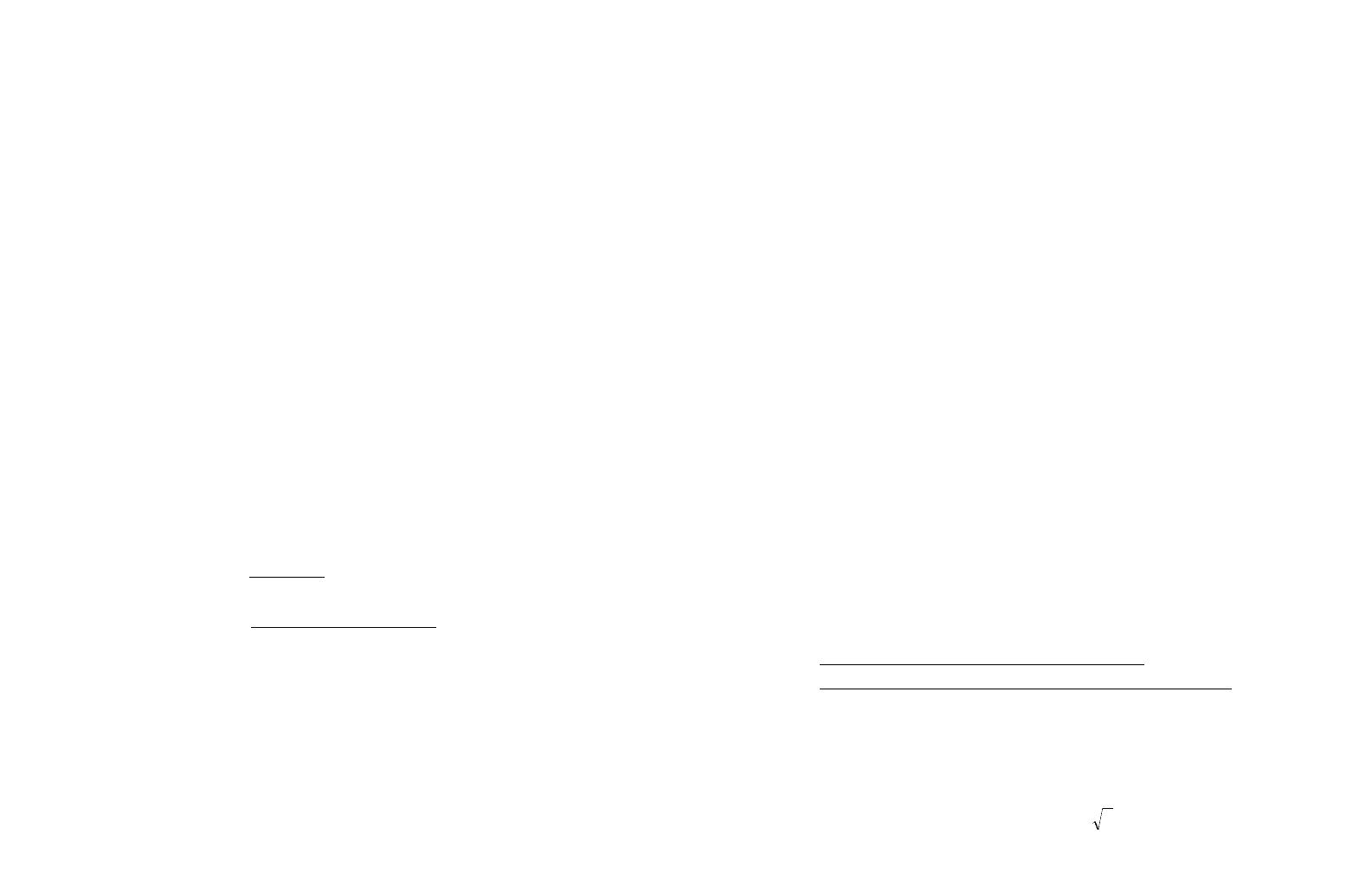
117

δ(τ) - дельта-функция, свойства которой задаются равенствами:

∫

=τδ







=τ∞

≠τ

=δ ,1)(

;0;

;0;0

)( dtt

причем второе равенство справедливо, если точка τ = 0 принадлежит ин-

тервалу интегрирования. Ясно, что белый шум, как и гаусссовский процесс,

нереализуем, поскольку в любом реальном случайном процессе два достаточ-

но близких значения всегда зависимы, а дисперсия процесса конечна. Оба эти

свойства в данном случае не выполняются. Несмотря на отмеченные факты,

модель белого шума широко применяется при конструировании моделей слу-

чайных процессов в составе так называемых формирующих фильтров.

Распределения вероятностей для белого шума в обычном смысле не су-

ществует, поскольку дисперсия (значение корреляционной функции в нуле)

равна бесконечности. Тем не менее, далее модель гауссовского белого шума

применяется достаточно широко. В основном это относится к моделям дис-

кретного времени, где такая модель становится реализуемой. Переход к моде-

ли дискретного времени предполагает осреднение непрерывного белого шума

на интервале дискретизации. При этом за дисперсию дискретного белого шума

принимается поделенная на интервал дискретизации интенсивность непре-

рывного белого шума.

Спектральные плотности, соответствующие корреляционным функциям

х1

(τ) и K

х4

(τ), описываются выражениями:

)4)((

)(2

)(

;

)(

222222

222

ωα+α−β−ωπ

β+αασ

=ω

α+ωπ

ασ

=ω

Марковский процесс описывается системой стохастических дифференци-

альных уравнений первого порядка, решением которой он является. Уравнения

системы характеризуются случайными начальными условиями и в правой час-

ти содержат случайные функции (процессы)

(t) = F(t) x(t) + G(t)w(t),

где x(t) - n-мерный вектор состояния;

F(t) - (п

n) - матрица динамики процесса x(t);

118

w(t) - векторный гауссовский белый шум единичной интенсивности;

G(t) - матрица, определяющая интенсивность процесса G(t)w(t).

Такой процесс называют диффузионным марковским процессом. Часто

уравнения называют формирующим фильтром, отмечая тем самым факт фор-

мирования разнообразных случайных процессов x(t) на основе процесса типа

белый шум.

Диффузионный марковский процесс, описываемый уравнением состоя-

ния, может быть как стационарным, так и нестационарным. Решение этого

уравнения определяется выражением

ττξτχ+χ=

∫

dGtttxtttx

)()(),()(),()(

000

где

),(

- фундаментальная матрица, с помощью которой решение уравне-

ния

(t) = F(t) x(t) записывается в виде:

)(),()(

txtttx

Математическое ожидание:

),()( mtttm

Если в момент времени t

математическое ожидание m

процесса не рав-

но нулю, то процесс x(t) характеризуется изменяющимся во времени матема-

тическим ожиданием от времени (по фундаментальной матрице:

),(

), т.е.

нестационарен.

Ковариационная матрица P(t) процесса удовлетворяет уравнению Рикка-

ти

)()()()()()()( tGtGtFtPtPtFtP

++=

т.е. в общем случае также является функцией времени. При т

= 0 процесс

будет стационарным, если матрицы F и G постоянны, матрица F устойчива, а

начальное значение P(t) совпадает с установившимся значением.

Примеры марковских случайных процессов.

Диффузионный марковский процесс первого порядка. Этот случайный

процесс описывается дифференциальным уравнением первого порядка

где α − постоянная положительная величина; w − случайный процесс ти-

па белый шум единичной интенсивности, для которого S

(ω) = l; g − коэффи-

циент интенсивности белого шума w (

qg =

, q −интенсивность белого шума).

Спектральная плотность стационарного решения имеет вид

119

)(

α+ω

=ω

Марковский процесс первого порядка в установившемся режиме харак-

теризуется корреляционной функцией

)exp()(

τα−σ=τ

и является недиф-

ференцируемым. Это, вообще говоря, следует также из того, что производная

процесса содержит белошумную составляющую. В связи с установленным

фактом недифференцируемости, следует обратить внимание на условность

использования в данном случае символа производной.

Диффузионный марковский процесс второго порядка. Этот случайный

процесс описывается дифференциальным уравнением второго порядка

0,2

>=++ hgwxkxhx

&&&

или в виде системы двух уравнений первого порядка

;

gwhxxkx

+−−=

где h и k - постоянные;

w - случайный процесс типа белый шум единичной интенсивности;

g - коэффициент интенсивности белого шума w .

Спектральная плотность стационарного решения имеет вид

4)(

)(2

)(

222222

222

ωα+α−β−ω

β+α

ασ

+ω+ω−

=ω

kih

где введены обозначения α = h, β = 22

hk −

2hkπ=σ

Данный марковский процесс характеризуется корреляционной функцией













τβ

+βττα−σ=τ sincos)exp()(

и является дифференцируемым.

8.1.1. Основные свойства марковских систем

Большое значение имеют марковские случайные процессы с дискретны-

ми состояниями и непрерывным временем.

Процессом с дискретными состояниями называется процесс, если его

возможные состояния S

, S

,... можно заранее перечислить (пронумеровать),

120

и переход системы из состояния в состояние происходит «скачком», практиче-

ски мгновенно. Процессом с непрерывным временем называется процесс, если

моменты возможных переходов из состояния в состояние не фиксированы за-

ранее, а неопределенны, случайны, если переход может осуществиться, в

принципе, в любой момент. Будем рассматривать только процессы с дискрет-

ными состояниями и непрерывным временем.

Пример такого процесса: система S состоит из двух узлов, каждый из ко-

торых в случайный момент времени может выйти из строя (отказать), после

чего начинается ремонт узла, тоже продолжающийся заранее неизвестное,

случайное время (рисунок 8.2). Состояния системы можно перечислить:

Рисунок 8.2. Граф отказов и восстановлений 2-х компонентной системы

- оба узла исправны,

- первый узел ремонтируется, второй исправен,

- второй узел ремонтируется, первый исправен,

- оба узла ремонтируются.

Переходы системы S из состояния в состояние происходят практически

мгновенно, в случайные моменты выхода из строя того или другого узла или

окончания ремонта.

При анализе случайных процессов с дискретными состояниями исполь-

зуют граф состояний. Состояния системы изображаются прямоугольниками

(или кругами, или даже точками), а возможные переходы из состояния в со-

стояние - стрелками, соединяющими состояния. Граф состояний для данного

примера представлен на рисунке. Стрелка, направленная из S

в S

, означает

переход в момент отказа первого узла; стрелка, направленная обратно, из S

,- переход в момент окончания ремонта этого узла. Остальные стрелки объ-

ясняются аналогично. Предполагается, что узлы выходят из строя независимо

друг от друга, а вероятностью строго одновременного выхода их из строя бес-

конечно мала.

Потоки событий в системах. Потоком событий называется последова-

тельность однородных событий следующих одно за другим в случайные мо-

менты времени. Например, поток отказов (сбоев) ЭВМ.