Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


164
Differential
Forms
6.1.1
The p-covectors
Antisymmetric
(0,
p)
tensors are calfed
pcovectors
or
pfomzs
and usudy de-
noted with small
Greek
letters. So
a
pfomn
w
is
a
function
w
:
(Xi
,...,
Xp)
F:
EX
x
E
-+
w(X1,
...,
Xp)
E
R,
which
is
ptimes linear; that
is,
for
all
i
=
1,2,.
.
.
,p
w(X~,
...,
Xi-l,~Yi+bZi,Xi+l,
...,
Xp)
=
aw(X1,.
. .
,
xi-1,
x,
Xi+l,
I.
.
,
X,)
f
bWk(X1,.
I
.
,
xi-1,
zi,
Xi+f,
f
.
I
,
xp>
;
(6.3)
0
completely antisymmetric
where
la\
=
0
or
1
according to the parity (even
or
odd, respectively)
of
the permutation
CJ
=
(il,.
. .
,ip)
of
(l,Z,.
.
,
,p).
The set
of
pcovectors
is
a
subspace
AP(E)
of
the vector space
q(E).
A
basis
of
Ap(E)
can be found by applying the usual procedures which require,
however, the notion
of
wedge
or
exterior
~d~~~
ofp
covectors.
6.1.2
The exterior product
Let
al,a2,
,
.
.
,
ap
be pcovectors
on
a vector space
E.
Their exterior product
a1
A
a2
A
-
-
A
aP
is
the pform
on
E
defined
by
that
is,
by the determinant
of
the matrix
(ai(Xj)).
by
(6.5)
is a pform.
The properties
of
the determinant show that the exterior product defined

The
Tensors
165
By using the procedure already used for 2-forms, it is easy to check that
any pform
w
can be written, in
a
given basis
(ei}
of
E,
&s
follows
with
wil...i,
=
w(ei,,
.
.
.
,
ei,)
and
(@}
the dual basis of
(ei}.
Thus,
the
(;)
=
n!/p!(n
-
p)!
distinct elements
make
a
basis
in the vector space,
Ap(E),
of the p-forms on E; that
is,
any
p-form
w
can be expressed in terms
of
them, and then
dimAp(E)
=
(;)
.
The
exterior
product
between a pform
a
E
Ap(E)
and
a q-form
p
E
AQ(E)
is
the
(p
+
q)-form
a
A
p
E
Ap+q(E)
defined
as
(QA
€)(XI,.
.
.
,
xk+Z)
=
C(-l)'"'a(xil,.
.
?
Xi,)p(xj,,
. .
xjl)
,
0
where the sum is over all permutation
(T
=
(il,
.
.
.
,
ik,jl,.
.
.
,
jl)
of
(1,.
.
.
,
k+l)
and
la1
=
0 or
1,
according to the parity (even or odd, respectively) of the
permutation.
It
is easy to verify that
0
a
A
/?
is truly a
(p
+
q)-form,
0
that the product is
0
anticommutative:
a
A
p
=
(-1)Pqp
A
a,
0
distributive with respect to the sum:
(aa+ba)AP
=
aa~p+ba~p,
0
associative:
(a
A
p)
A
7
=
a
A
(p
A
r),
0
coincides with the product defined by
Eq.
(6.5)
if
a
and
p
are
monomials; that
is,
if
a
is the exterior product
of
p
covectors
a1,.
. .
,
ap
and
p
is the exterior product of
q
covectors
PI,.
.
.
,
p,,
respectively:
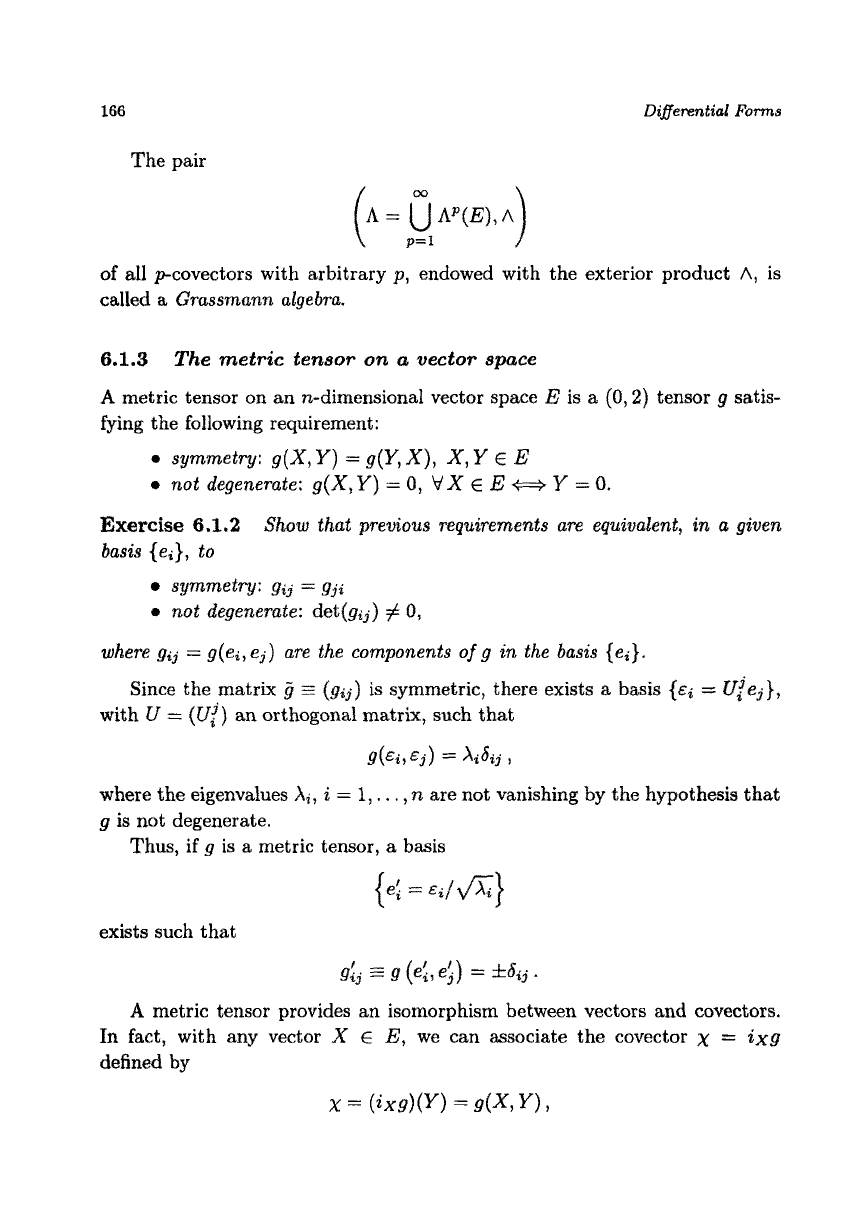
166
The pair
Differential
Forms
of
all
pcovectors with arbitrary
p,
endowed with the exterior product
A,
is
called
a
Grassmann algebra.
6.1.3
A
metric tensor
on
an n-dimensional vector space
E
is
a
(0,Z)
tensor
g
satis-
fying the following requirement:
The
metric tensor on
a
vector space
0
symmetry: g(X,
Y)
=
g(Y,
X),
X,
Y
E
E
0
not degenerate:
g(X,Y)
=
0,
VX
E
E
t3
Y
=
0.
Exercise
6.1.2
basis {e,},
to
Show
that previous ~equ~~ements are equivalent,
in
a given
symmetry: gij
=
gji
*
not degenerate:
det(gdj)
#
0,
where gcj
=
g(ei, ej) are the components ofg
in
the
basis
{ei}.
with
U
=
(U,”)
an orthogonal matrix, such that
Since the matrix
=
(gij)
is
symmetric, there exists
a
basis
{ci
=
U!ej},
g(Ei,Ej)
=
Mij
>
where the eigenvalues
Xi,
i
=
1,.
.
.
,
n
are not vanishing
by
the hypothesis that
g
is
not degenerate.
Thus, if
g
is
a
metric tensor,
a
basis
exists such that
gLj
z
g
(ei3 ei)
=
;tSij.
A
metric tensor provides an isomorphism between vectors and covectors.
In
fact, with any vector
X
E
E,
we can associate the covector
x
=
ixg
defined by

The
Tensor
Fields
167
whose components in
a
given basis are
xj
E
(iX9)j
=
x4g*j.
xi
=
gyyj,
Since det(gij)
f
0,
the previous map
is
invertible,
so
that
.*
where
(9'j-i)
is
the inverse of
(gij)
defined by
ih
9
ghj
=
6ij
6.2
The
Tensor
Fields
A
(m,
n)-tgpe
tensor
field
S
on
a
manifold
M
is
a
rule that associates, with
every point
p
E
M,
a
(rn,n)-type tensor
S,
E
TT(7,M);
i.e.
a
map
S
:
p
E
U
C
M
+
S(p)
=
S,
E
r(T,M).
By applying the same algebraic procedure
used
to
obtain the
Eq.
(6.2),
it
is
easy
to
see that, in
a
local coordinate system,
a
tensor
field
S
can be written
in
the form
where
si
=
cp'(p)
are the coordinate
of
p
in the chart
{U,
cp).
The tensor field
S(p)
is
said
to
be
Ch
~z~ere~t~~ble
on
a
Ck
manifold
M,
with
h
5
k
-
1,
if
the bctions
S$::i(p)
are
Ch
differentiable on the manifold
M.
6.2.1
Since the Lie derivative has been defined on functions,
differentia^
1-forms and
vector field, it is also defined, by the Leibnitz rule, on
a
general tensor field
as
the one given in
Eq.
(6.7).
One
of
the most important use of the
Lie
derivative in physics
is
to
check
if
a
tensor field
is
invariant under some transformation.
If
the transformation
is generated by some vector field
A,
then the invariance
of
the tensor field
S
is
expressed
by
The
Lie
derivative
of
a
tensor
field
LdS===O.

16%
Difleerentid
Foms
The invariance condition preserves its elegance, also locally.
For instance, let the
mixed
tensor field
s
:
(X,
a)
+
sjx,
a)
be
locally represented
by
Its Lie derivative, with respect to the vector field
A,
is given
by
Thus, the invariance
of
S
is
expressed by
In
terms
of
the matrices
it
can
be written
as
follows:
dr
For the interested reader, an intrinsic ~e~nition
can
be given
as
in the case
The
Lie
derivative, with respect
to
X
of
a tensor field
S,
is
defined
by
of
a
vector field.

The
Tensor
Fields
169
where
+r
is the flow of the vector field
X
bT
:p~
M
+br'(P)
EM,
0
(@)*
its derivative
to the whole tensor algebra
m,n=O
Thus, in our case
(4-T)*bqp)
:
~(f(P))
+
7(P)
*
This
definition can appear formally complicated. In reality it is very simple
from
a
geometrical point
of
view.
As
a
matter
of
fact, a map
4
between
two
manifolds
M
and
N,
transforms
a
curve trough
p
E
M
to
a
curve trough
the point
&(p)
E
N;
then, it also transforms
a
tangent vector to
M
at
p
in
a tangent vector to
JV
at
+(p).
So
4
induces
a
map,
&,
between the corre-
sponding tangent spaces
7,M
and
T&,)N
at
corresponding points.
Of
course,
it
also
induces maps between the tensor spaces
zm(7,M)
and
zm(%T(,>M)
at
corresponding points and, finally, between
7(p)
=
C&,=a
xm(7,M)
and
7(dT7(p))
=
CZ,n=o
%m(%~(p)M).
If
S
is
a
(1,~)-tensor field, the relation
(a)
S(Y1,
Y2,.
.
,
,
Y'))
E
S(a,
Yl)
Y2,.
.
.
,
Y')
defines
a
vector field
s(Y1,Y2,.
.
.
,Yr).
It
can
be easily proven that,
for
any vector field
X,
we have
(LXS)(Y')Y2,.
. .
,Y')
=
[X,S(Y',Y2,.
.
*
,
Y')]
T
-
s(Y1,.
. .
,
[X,
Yi],
.
.
.
,
Y')
.
(6.10)
i=
1

170
Daflerential
Forms
The Leibnitz rule gives the following general properties of the Lie derivative:
(6.11)
Lx(R
@
S)
=
(Lx
R)
€?J
s
+
R
63
(Lx
S)
,
Lx(T(ff1,
*.
.
,
ap,
x1,.
*
.
,
X,))
=
(LxT)(a1,.
.
.
,
ffp,
x1,
. .
.
,
X,)
tl
+
c
T(a1,.
.
.
,
LXW,.
.
*
,
ap,
x1,
.
.
*
,
X,)
i=l
Equation (6.10)
is
just
a
particular case of Eq. (6.12).
Exercise
6.2.1
Show
that
for any vector fields
X
and
Y
:
6.2.2
The differential
p-forms
A
diflerential
1-form
a
on the manifold
M
is
a
regular map
a:TM+R
(6.13)
of
the tangent bundle of the manifold
M
in
R,
linear in every tangent space
7,M:
ap(aX+bY)=aap(X)+bap(Y),
Va,bEX,
VX,Y
ETM.
In this way,
a
differential 1-form on
M
is
a
covector on
7,M
differentiable in
p.
Let
us
suppose that the functions
d,
.
. .
,
zn
are a system of local coordinates
in
a
given domain
U
of the manifold
M
,
zi
:
po
E
u
-+
2(po)
=
z;
E
8
vi
=
1,
.
.
.
,
n
*
These functions are differentiable, and their differentials
dzk,
at
the
point
PO,
dxko
:
X
E
TOM
+
dzk,,
(X)
E
!R
V
i
=
1,
.
,
. ,
n
,
are covectors on
TOM.

The
Tensor
Fields
171
The values of the differentials
dxbo,.
.
.
,
dzgo
on the vector
X
are the com-
If
am
is
any covector
on
&,N,
because of the linearity of
ape,
we have
ponents
X',
.
.
.
,
X"
of the vector.
=
(ai(Po)dz;o
,
X)
,
with
The covector
apo
can thus be expressed locally in the form
Qpo
=
al(po)dz;o
+
*
'
*
+
a,(po)dzjf,
Therefore, every differential 1-form
a
(Eq.
(6.13)) in the domain
U
can be
locally expressed
as
Q
=
q(p)dx'
+
*.
.
+
a,(p)dz"
.
A
Ic-covector
wp
at the point
p
E
M
is a k-times linear (Eq. (6.3)) and
antisymmetric
(Eq.
(6.4)) function,
up
:
(XI,..
.
,Xk)
E
GM
X
X
&M
+
wp(X1,..
.
,Xk)
E
8.
(6.14)
A
di8erentira.l
k-form
w
is
defined on the manifold
M
if the form
(Eq.
(6.14))
Every differential k-form
w
can be uniquely expressed in a domain with
is
given
at
every point
p
in
M
and, moreover,
if
it is differentiable.
local
coordinates
I'
,
,
.
.
,
z"
as
zl...ik
(d,
.
.
.
,
zn)dZil
A
.
*
A
dxik
,
(6.15)
where
dxil
A
A
dxik
are the exterior products of the basis 1-forms
Operations such
as
the sum
of
k-forms, the product with real numbers, the
exterior product between forms are always point-wise possible; that
is,
at every
1
k!
w
=
-w'
dxl,
.
.
.
,
dzn.

point
p
E
M
the corresponding exterior forms on the tangent spaces
T,N
can
be summed and multiplied with numbers
or
exteriorly.
Lie derivative
of
a
differential
k-form
F'rom
Eq.
(6.9),
defining the Lie derivative of a tensor field, we obtain, for a
differential k-form
w,
the useful formula
(L*w)(Y',Y2,.
.
.
,Yk)
=
(X,W(Y',Y2,
*
.
.
,Yk)]
which
is
similar to the one given, for
a
(1,
k)-tensor field, by the
Eq.
(6.10).
6.2.3
The
exterior derivative
On
the space
of
differential k-forms we can define an operator
d,
called
exterior
derivative,
having the following properties:
If
a
E
Ak(M),
,1!3
E
ifk(&),
y
E
A~(M),
(1)
d(..
4-
P}
=
da
+
dp;
(2)
d(a
A
yf
=
da
A
r
+
(-l)k~
A
dr;
(3)
d2a
=
0;
(4)
On the differential 0-forms; that is, on functions, the operator
d
coin-
cides with the differential defined in Sec. 5.5.
The operator
d,
as
it easily follows from its properties, transforms differen-
tial k-forms in differential
(k
t
1)-forms.
By
using the properties
(l),
(2),
(3)
and
(4),
we can easily calculate the
exterior derivative
of
a
k-form
in a coordinate
basis.
For
w
given by
Eq.
(6.15),
we obtain
because
ddxi
=
0.

The
Tensor
Fields
173
6.2.4
A
differential k-form
is
said to be
closed
if
closed and exact diflerential
forms
dw
=O,
and to be
exact
if there exists
a
E
Ak-l(M),
such that
w=da.
Since
dl
=
0,
an exact pform
is
also closed. The converse is not true and
the following
is
a
classical example in
R2,
Example
23
Consider the differential
1-form
xdy
-
ydx
W=
X2fY2
which
it
is
easy to see
to
be closed,
h=O.
In
polar coordinates
x=rcosd,
y
=
rsind,
it
becomes
Thus,
one
is
tempted to say that
w
is
an exact differential
form
also.
But
the
angles do not exist really!
The misunderstanding is solved by obseruing that
w
is not defined at the
point
(0,
0),
as well as the transformation
from
Cartesian to polar coordinates.
6.2.5
The contraction operator
ix
Let
E
be
an n-dimensional vector space and
hT(E)
be
the vector space of
r-covectors defined on it.
If
w
E
A'(E)
is an antisymmetric multilinear map from
E
x
E
x
-
.
x
E
-
to
R,
and
XI, X2,.
. .
X,
are vectors of
El
then
4x1,
x2
* *
.
Xr)
(6.17)
