Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


174
Dzflerentiol
Forms
is
a
real number antisymmetric under the interchange
of
any two vectors.
Therefore, an r-covector is defined once the number
(Eq.
(6.17)) is given
VXi,
i
=
1,.
.
.
,r.
It
is natural, starting
from
any r-covector
w
E
A'(E)
and a vector
X
E
El
to define a
(r
-
1)-covector, namely
ixw
E
A'-'(E)
by
the following equality:
(ixw)(X,,
x2,.
..
X?.-I)
:=
W(X,
Xl,
xz,
.
.
.
Xr-1).
In this way,
(ixw)
is
the
(r
-
1)-covector, built from
w
f
A'(E)
and
X
E
El
which evaluated on
(T
-
1)
vectors
XI
,
XZ,
. .
.
X,--l,
gives the same real number
given by
w
on
the
r
vectors
X,Xi,X2,.
.
.
Xr-l.
The operator
ix
is called the contraction operator with respect to
X.
We
already met it in the case
in
which
w
is
a simple covector.
In
fact, by denoting
with
CY
an element
of
A'(E)
=
h(E)
=
E*,
the previous definition simply
reduces to
ixCY
=
a(X)
5
(a,
X)
In order to illustrate the given definition, let
us
represent the r-covector
w
in
a
basis
(~92)~
as
follows:
(6.18)
1
w
=
-wij...kdi
A
6'
A
*
*
*
A
8"
r!
Thus,
1
(ix,w)(X2,.
.
.
,XT)
=:
2wili
2...ir
det
1
(6.19)
and then, by using the Laplace expansion
(first
column)
of
the deter~inant,
ixw
is represented
by

The Tenaor Fields
175
What are the properties of the operator
ix?
0
It is easy to see that
ixiy=-iyix
(6.21)
(6.22)
This easily follows by observing that,
'dw
E
A'(E),
w(X,
Y,
XI,
x2,
.
.
Xr-2)
=
(ixw)(Y,
x1,
x2,.
*.
xr-2)
=
(iyixw)(Xl,x2,
...
xr-2)
W(Y,X,Xl,XZ,.
1
.x4
=
(iYW)(X,Xl,X2,.
.
.Xr-2)
=
(ixiyw)(X1,
x2,.
. .
Xr-2)
.
As
a
particular
case,
it follows that
ia
=o.
(6.23)
0
If
a
E
Ar(E),
and
p
E
h5(E),
with
r
+
s
I
n,
then
This easily follows from the following formula:
where the sum is over all permutation
(jl,
$2,.
.
.
,
jr+s)
of
(1,2,
.
. .
,
r
+
s)
and
CT
=
0
or
1,
according to its parity (even
or
odd, respectively).
Properties
of
Eqs.
(6.23)
and
(6.24)
extend in
a
natural way, with the only
additional requirement that on 0-forms
f
E
.F(M),
ixf
=
0,
to r-forms on
a
differential manifold
M.
Let
X
be
a
vector
field
on
M
and
a
E
hk(M).

176
Da;tferentiaf
Forms
The operator
ix
which, acting on the differential k-form
a,
transforms it
in
a
differential
(k
-
1)-form
ixa
(also called
interior
product
between
X
and
a),
is
defined po~nt-wise
as
(ixa)p(xl,.
xk-1)
==
ap(x(P),
XI,
* *
*
,xk-1)
1
\JP
E
M,
(6.25)
where
XI,.
.
.
,
Xk-1
are tangent vectors to
M
at
p.
The
ix
operator fulfills the following properties:
(1)
ix(a1+
(22)
=
ixa1f
ixff2;
(2)
ix(a
A
P)
=
ixa
A
p
+
(-I)~cx
A
ixp;
(3)
if
Q:
E
A'(M),
(ixa)(p)
=
(X(P),
a*)
=
ap(X(II)));
(4)
iff
is
a
0-form,
then
ix
f
=
0.
Thus, the properties
of
the interior product
ix
on
a
differential manifold
M
are a~gebraically similar to the ones of the exterior derivative
d,
namely
d2
=
0,
d(a
A@)
=
(da)
AP
+
(-1)'a
A
dP.
Of course,
ix
:
A'(M)
-+
Ar-'(M)
d
:
h'(M)
+
Ars'(M),
and
ixd
:
A'(M)
-+
A'(M)
dix
:
A'(M)
-+
Ar(M).
The operators
ixd
and
dix
do not coincide,
as
it
is
easy to verify
on
the
simple example of
a
=
dxi
.
Indeed, denoting with
Xi
the components in the
basis
fa/8xi}
of the vector field
X,
we get
(ixd)d~'
=
0
,
(dix)dzi
=
d(ixdzi)
=
dXi
=
-dd.
(6.26)
8X'
Moreover, the operators
ixd
and
dix
are not derivations, since
ixd(a
A
p)
=
ix[(daaf
A
p
+
(-l)ra
A
dp]

The
Tensor
Fields
177
=
(ixda)
Ap
+
(-l)'+'(da)
A
ixp
+
(--l)'(iXa)
A
dp
+
(-1)'+'o
A
ixdp,
and
dix(cuAp)
=
d[(ixda)AP+
(-1)'aAixp]
=
&[(ixa)
A
p]
+
(-1)'d[a
A
ixp]
=
(dixa)
A
p
+
(-l)'+'(ix~)
A
dp
+
(-l)r(d~)
A
ixp
+
(-1)"'a
A
dixP.
However, by adding
ixd(a:
A
p)
and
dix(a
A
p)
from
the above relations,
we obtain the result that the operator
ixd
+
dix
is
a
derivation, since
(ixd
+
dix)(a
A
P)
=
[(ixd
+
dix)a]
A
p
+
a
A
(ixd
+
dix)P.
(6.27)
Finally, let
us
remark that the three operators
Lx,
ix
and
d
are not inde-
pendent on
A'(M).
It
is
easy to
see
that, on r-forms
w
E
A'(M),
they
satisfy
a
very
useful
relation, the so-called
homotopic
or
Cartan identity:
Lxw
=
ixdu
+
dixw
,
(6.28)
or
in operator terms,
Lx=ixod+doix.
Pro0
f,
0
Iff
E
F(M)
=
A'(M),
since
ixf
=
0,
we
have
ixdf
+
dix
f
=
ixdf
=
(df)(X)
=
Xf
=
Lxf
,
0
For
a
generic
1-form
cr
=
fdg
E
A(M):
ixda
=
ix(df
A
dg)
=
(Xf)dg
-
(df)Xg,
dixa
=
d(fXg)
=
(df)Xg
+
fd(Xg).
(6.29)
(6.30)

178
Thus,
ixda
+
dixa
=
(Xffdg
+
fd(Xg)
=
(Lxf)dg
+
fLxdg
=
LXQ,
(6.31)
where the Cartan identity on functions has been used:
fd(Xg)
=
fd(ixdg)
=
f(dix)dg
=
f(&x
+
ixd)dg
=
fLxdg.
The proof proceeds now by induction.
A
more elegant proof can be found in the Kobayashi-Nornizu
book,
and
it
consists in observing that
(1)
ixd
+
dix
is
a
derivation of degree
0;
(2)
every derivation
of
degree
0
commuting with
d
is
the
Lie
derivative
with respect to some vector field;
(3)
the derivations
Lx
and
ixd
+
dix
give the same result
on
f
E
F(M).
From
Eq.
(6.29)
directly follows the useful formulae
6.2.6
A
~~~e~~t
pr0cedup.e
The fact that the
three
operators
d,
Lx
and
ix
are not ~nde~endent on differ-
ential forms, suggests the following different procedure to define
the
exterior
derivative in terms
of
the interior product and the Lie derivative.
Let
us
observe that, by using the Cartan identity, we have
0
for a function
f:
ixdf
==
(df,X)
E
Lx
f
,
0
for
a
differential 1-form
a
E
h(M):
(dff)(X,
Y)
=
iyixda
=
iy(Lxa
-
dixff)
=
(Lxa,
Y}
-
iy(dixa)
=
(Lxa,
Y)
-
iyd(ixa)
=
(Lxa,
Y)
-
LY
(a,
X)

The Tensor
Fields
179
where the property that
f
zi
ixa!
=
(a,
X)
is
a
function, to which the previous
formula
can
be applied, and the Leibnitz rule has been used,
0
for
a
differential 2-form
w
E
A2(M):
0
for
a
function
f,
as
0
for a differential 1-form
a
E
A(M),
as
(da)(X,
Y)
-=
(Lxa,
Y)
-
(LY%
X)
+
(0,
[X,
Y])
,
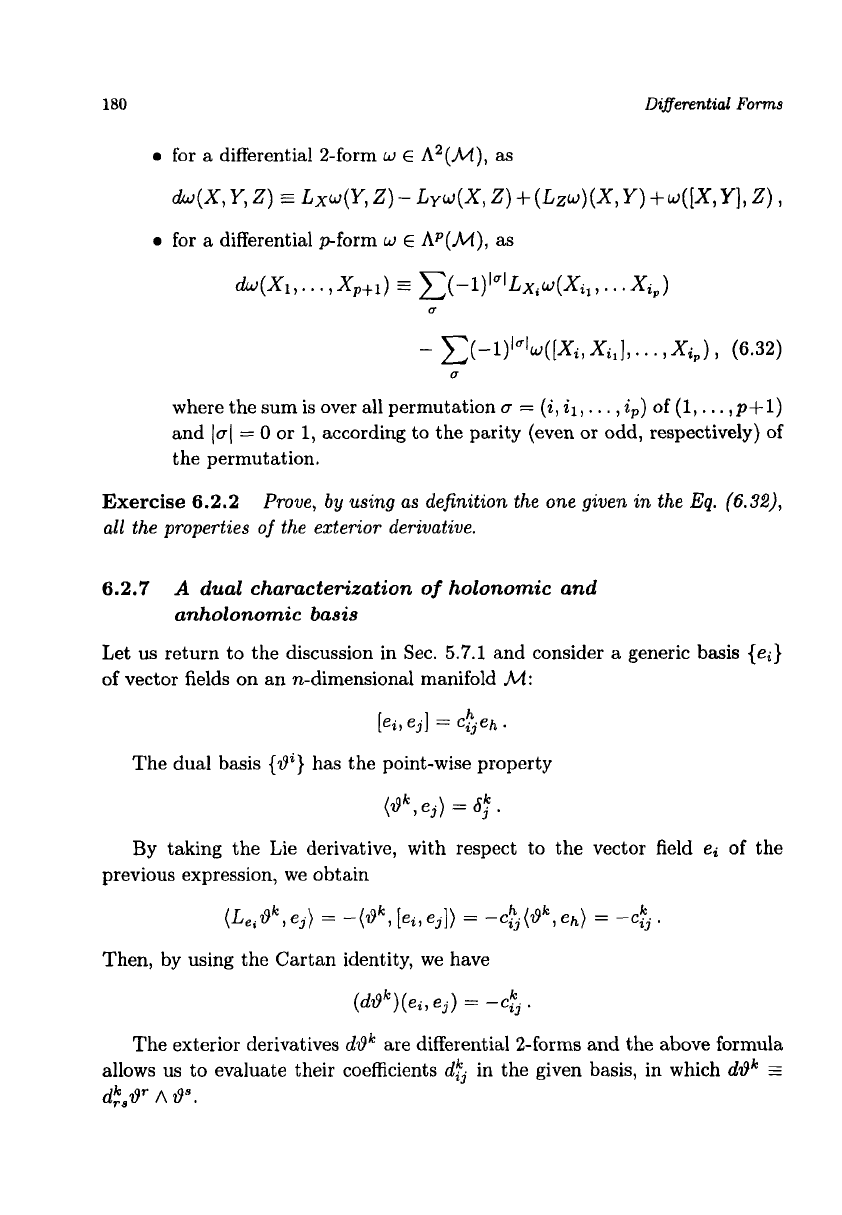
180
Daflerentaol
Forms
0
for
a
differential 2-form
w
E
A2(M),
as
&(X,
y,
2)
=
LXW(Y,
2)
-
LYW(X,
2)
+
(LZW)(X,
Y)
+W([X,
Y],
2)
1
0
for
a
differential pform
w
E
hP(M),
as
&(XI,.
. .
,
X,,,)
E
~(-l)l"lLxiw(xa,,
. .
.Xi,)
-
C(-l)'"'W([Xi, Xil],
. .
.
,Xi,),
(6.32)
where the sum
is
over
all
permutation
o
=
(i,
il,
. .
.
,
ip)
of
(1,.
. .
,p+l)
and
lo(
=
0
or
1,
according to the parity (even
or
odd, respectively)
of
the permutation.
U
Exercise
6.2.2
all
the properties
of
the exterior derivative.
Prove,
by
using as definition the one given in the
Eq.
(6.32),
6.2.7
A
dual characterization
of
holonomic and
anholonomic basis
Let us return to the discussion in Sec.
5.7.1
and consider
a
generic
basis
{ei}
of
vector fields on an n-dimensional manifold
M:
[ei, ejl
=
c$eh.
The dual basis
{gi}
has the point-wise property
(Sk,ej)
=
hj
k
.
By taking the Lie derivative, with respect to the vector field
ei
of the
previous expression, we obtain
(Lei8',ej)
=
-(6',[[e,
e.1)
=
-c$(6',eh)
=
-cij.
k
z,
3
Then, by using the Cartan identity, we have
(ddk)(ei, ej)
=
-cFj
.
The exterior derivatives
ddk
are differential 2-forms and the above formula
allows us to evaluate their coefficients
dfj
in the given basis, in which
ddk
=
dF,d'
A
6".

The
Metric
Tensor
Field
on
a
Manifold
181
We obtain
d,k,(Sr
A
P)(e,, ej)
=
-~tj,
or
2dFj
=
-caj
k
I
Therefore, the elements of the dual basis
{Sa}
have the following property:
(6.33)
dt?k
f
--cijS
lki
A@.
'
2
We
can
summarize the previous results
as
follows:
If
{ei}
is a basis
of
vector fields and
{di}
its dual basis on an n-dimensional
manifold
M,
then
1
2
[e,, ej]
=
ckeh
H
dSk
=
---cfj29'
A@.
Therefore, for
a
holonomic basis, given
c&
=
0,
the dual basis consists of closed
differential 1-forms
Sk,
dSk
=
0,
and then, locally, coordinates functions
{zi}
exist such that
k
dk
=
dx
.
As
B
consequence,
a
axi
*
ei
=
-
Thus,
besides the one given in Sec. 5.7.1, a new characterization of
a
holonomic
basis {ei} is given by the closure property
of
the differential 1-form which
composes its dual basis.
6.3
The
Metric Tensor Field
on
a Manifold
A
metric tensor field
g
on a manifold
M
is a rule that associates with every
point
p
E
M
a symmetric and not degenerate (0,2)-tensor
g(p).
Thus, at every point
p
E
M,
g(p)
is
a metric tensor for the tangent space
T,M,
and the considerations, already done for
a
metric tensor on
a
vector
space, can be repeated. In particular, in every tangent space
7,M,
a
basis can
be chosen such that
gij
(p)
=
rtdij.

182
Dafferential
Forms
Since
a
metric tensor field is required to be at least continuous and integers
do not change continuously, the
canonical
form
of
g
has to be constant every-
where and we speak of
signature
of
the field
g.
The collection
of
the bases in
which
g
takes on the canonical form, defines a globally orthonormal basis on
M,
but this global basis is not generally
a
coordinate basis.
In this sense the space
Xn,
considered as a manifold endowed with the
Euclidean metric tensor field
(6ij
at every point), constitutes just an excep-
tional case.
Even in that case only the Cartesian coordinates generate an
orthonormal basis.
6.3.1.
Killing
vector
fields
The Killing vector fields play a relevant role in the study
of
the isometries
of
a
metric tensor field; this is why they are usually used in general relativity.
They are defined to be the vector fields
A
preserving a metric tensor field
g;
that is, by the invariance condition
The above equation, given
g,
admits very few solutions for
A.
Let the metric tensor field
9
:
(X,Y)
-+
g(X,Y)
be locally represented
by
g
=
gijdxi
8
dxj.
Its Lie derivative, with respect to the vector field
A,
is given by
LAg
=
LA(gijdxi
@
dxj)
=
(LAgij)dXi
8
dd
+
gij(LAdXi)
8
dxj
+
gijdxi
8
(Lad.')
Thus, the invariance of
g
is expressed by
(6.34)
(6.35)

The
Metric Tensor
Field
on
a
Manifold
183
In terms
of
the matrices
Eq,
(6.35)
can be written
ELS
foIIows:
where the symbol
T
denotes matrix transposition.
6.3.2
~~ima~~~ symmetric
manifolds
We may now
ask
the following question: how many vector fields, leaving
a
metric tensor field
9
invariant, exist on an n-dimensional manifold
M?
By
introducing the differential l-form
t
by
(4,
x>
=
s(4
XI
8
Eq.
(6.35)
can also be written in the following form:
where
(6.36)
(6.37)
are called the
~hr~s~~~~l
s~~boZs.
The
number of independent differential equations, in the partial differential
system
(6.36),
is
(1/2)n~n
+
l),
while the number
of
unknown functions
<
is
n,
so
that the system
(6.36)
is
overdetermined for
n
>
I,
and the number of
Killing vectors will
be
upper-bounded,
By
taking the derivative of
Eq.
(6.361,
we obtain
(6.38)
By adding the above equation to itself with the permutation
(i
-+
j,j
-+
i,
k
-+
j)
of the indices, and subtracting the one with the permutation
(i
-+
j,j
-+
k,
Ic
--+
i},
we finally obtain
