Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


184
Differential
Forms
where
is
a
function
of
gij
and its first and second derivatives.
Thus, once the metric tensor field
g
is given and the functions
4's
and
its
first derivatives are known at
a
point
p
E
M,
the above equation allows
us
also to know the vaiue, at the point
p,
of
the second derivatives
of
the
('s.
In
the same way, by successively differentiating the equation, we can determine
all higher derivatives
of
the
['s
at
the point
p.
This suffices,
if
the manifold
M
is analytic, to determine the differential 1-form
5
everywhere.
at
p
determine, via Eq.
(6,38),
the symmetric
part of the
first
derivatives
&i/azj,
we
conclude that every Killing vector on
M
is
determined by giving the values
is
a function
of
gij
and its first derivatives, and
Since the assignment of
at
any
point
p
E
M.
Therefore, since the number
N
of the parameters
ai
and
bij
is given by
1
I
N
=
n
+
-n(n
-
1)
=
-n(n
+
I),
2 2
on
an n-dimensional manifold
M
there exist at most
(1/2)n(n
+
1)
Killing
vectors,
6
for
n
=
3.
It
is
worth observing that Eq.
(6.36)
may not admit solutions.
An
n-manifold
M,
endowed with a metric tensor field,
is
said to
be
maxi-
malty
symmetric
if,
on
it,
there exist
(1/2)n(n
+
1)
Killing vectors.
6.3.3
On
a
differential manifold
M
there exist only three natural
derivat~o~~,
which
are given by the
Lie derivative,
the
interior
product
and the
exterior derivative.
Moreover, on differential forms they are not independent, because of the Cartan
identity
The
Levi- Civita covariant derivative
Lx
=
ixd
+
dix
,
However, once a metric tensor field
g
is
given on
a
manifold
M,
a
new deriva-
tion, the
Levi-Ci~ta covariant de~vative
Vx
with respect to the vec~o~~eld

The Metric Tensor
Field
on a Manifold
185
X,
can be defined by
(6.39)
where
f,
a
and
Y
are a differentiable function, a differential 1-form and a
vector field, respectively, and where
X,
is the vector field associated to
CY
via
the metric tensor field
9;
i.e.
or,
symbolically
x,
=
g-l(a).
We notice that
(Vxa)(Y)
is the
sum
of two terms which are antisymmetric
and symmetric, respectively, under the interchange
X
t)
Y.
The Levi-Civita covariant derivative can be naturally extended to vector
fields by the Leibnitz rule; that is, by
(a,
VXY)
=
LX(% Y)
-
(VX%
y>.
From
Eqs.
(6.39),
it easily follows that the Levi-Civita covariant derivative
is
3-linear; that
is,
the following property holds:
Vfx=fVx,
Qf
€3(M).
It is worth recalling that the same property does not hold for the
Lie
derivative; i.e.
LfX
#
fLx
1
unless when applied to functions.
We have
Let
us
evaluate the Levi-Civita covariant derivative in a basis
{ej},
{di}.
x
=
xiei,
Y
=
Yiej,
a
=
adi
)
g
=
gijOa8
IJJ
,
so
that
..
X,
=
gZ3ajei
,

so
that
(6.40)

The
Metric
Tensor
Field
on a Manifold
187
with
hk
1
1
r$
=
-9
(ej(gki)
+
ei(gkj)
-
ek(gij)
-
glicfik
-
gljcil,
+
gklcij)
.
2
The above quantities, which are also called the
~evi-C~~ta connectio~
co-
efficients,
in
a
holonomic basis reduce to the
Christoffel
symbols
given by
Eq.
(6.37).
They are not the components of any tensor and have the
PrOpertY
r$-r;i-c$
=o.
(6.41)
Exercise
6.3.1
Show
that,
in
a
give^
basis
VXY
=
Xi[ei(Yj)
-
T~;~Y=+~,
so
that
V,iej
=
r;{eh.
The
covariant derivative can be extended
to
any tensor field
by
the
Leibnitz
rule,
so
that
Vx(S@TTj
=
(VxS)@T+S@VxT.
Exercise
6.3.2
tensor
field
vanishes; i.e.
Show that the Levi-Civita covariant derivative
of
the metric
vxg=o.
Equation
(6.40),
for
a
=
dh
and
X
=
e,,
gives
V,@
=
-r;Q9j,
and can be taken
as
a
starting point to define
a
more
general
covariant
deriva-
tive,
without use of any metrics, but we will not go on further on this subject.
A
purely algebraic formu~ation can be found in Ref.
125.
Equation
(6.41)
expresses, in
a
given basis, the vanishing
of
the
(1,
P)-tensor
field defined by
T(a,
x,
Y)
=
(a,
VXY
-
vyx
-
[X,
Y])
,
which
is
called the
torsion
of
the connection
V.

188
Dafferential
Forms
Exercise 6.3.3
basis,
Show that actua~ly
7
is
a
tensor field
and
that,
an
a
given
Thus, the Levi-Civita covariant derivative has vanishing torsion and
fulfills
the property
Vxg
=
0.
It
can
be
shown
that,
given
a
metrics on
a
manifold, the
only torsionless connection
for
which
Vxg
=
0
is
the Levi-Civita c~nnection.~~
6.3.4
The
R~~~~nn
tensor
field
The Riemann* (1,3)-tensor field
R
is
defined by
where the
R(X,
Y)
is the
curvature operator
of
V,
defined by
Exercise 6.3.4
that
is,
it
is
~-~~~~zZ~~ear.
Exercise 6.3.5
Show that actually
R,
defined by
Eq.
(6.42),
is
a tensor field;
Show that,
in
a
given basis,
Exercise 6.3.6
adent~t~
Show that the covariant derivative
V
satisfies the Jacobi
Px, [VY,
VZ]]
+
IVY, [VZ, Ox]]
4-
[VZ, [Vx, Vy]]
=
0
8
*Georg Friedrik Bernhard Riemann waa born in Breselenz
on
September
17,
1826
and
died in Selasca on July
20,
1866.
He studied at Gottingen under Gauss, and subsequently
at
Berlin under
Jacobi,
Dirichlet, Steiner and Eisenstein,
all
of
whom were professors there
at
the same time,
In
spite of poverty and sickness he struggled to pursue
his
researches.
Riemann
was
one
of
the most profound and brilliant mathematicians
of
his time.
In
1857 he
was
made professor
at
Gottingen.

The
Metric
Tensor
Field on
a
Manifold
189
Show
aka
that in a coordanates
basis
the above equation reduces to the so-called
Biancht? ~dentit~e§
0.3.5
The
RiccP tensor
is
the (0,2)-tensor field, which
is
defined in a coordinate
basis
by
The
Rice;
tensor
and
the
ecalar
czlruature
71.j
=
z!kj
3
and
it
is
a
symmetric tensor field
Rij
=
Rji
.
The
scalar ~u~ut~~
is
defined
by
Exercise
6.3.7
also
that the cont~acte~ ~zanchz i~en~it~es
Show that the Ricci tensor is a symmetric tensor field. Show
t
Luigi Bianchi was born in Parma in
1856
and died in
Pisa
in
1928.
He has been
a
student
of
E.
Betti and U. Dini in Pisa, and of
F.
Klein in Gottingen. He
was
a
professor
at
the
University and Scuola Normale Superiore in Pisa. He has been one
of
the most important
Italian mathematicians in the
last
century. His works till up more than
10
volumes and
concern mainly differential geometry and number theory. Both the original papers and the,
now classical, books (on differential geometry, transformations groups, elliptic function) are
written in
a
very
transparent and elegant form. Bianchi
was
strongly loved by his students
not
only
for
the marked
vis
comfca
(funny spirit), which
was
one of his characteristic features.
tGregorio Flicci-Curbastro
was
born in Lug0 (Ravenna) in
1853
and died in Bologna in
1929.
He
atudied
at
Rome, Bofogna
and
Pisa
Universities where he obtained
his
degree
in
1875.
He
has
been
a
student of
F.
Klein, in Gottingen, and teaching assistant of U. Dini
in
Pisa.
He has been
a
professor of mathematical physics
at
Padova University from the
year
1880.
The main scientific ~ntribution
of
Ricci has been the invention (together with
its student Levi-Civita)
of
the absolute differential calculus, later an essential tool
for
the
formulation
of
general relativity.

190 Diflerential
Forms
The previous tensor fields play a basic role in Einstein§ general relativity in
which space-time is represented
as
a 4-dimensional manifold with
a
metric ten-
sor
field
g
representing the ~ravitational
field.
The
empty-space ~ravitationai
field
g
is
found by solving Einstein’s field equations
8.4
Endomorphisms
Associated
with
a
Mixed Tensor
Field
Let
T
be a
mized tensor field;
that is, a tensor field
of
type
(1,
l),
on the
n-dimensional manifold
M.
In
a
coordinate basis it can be written
as
Let
7,M
be the tangent space to the manifold at
dual.
(6.43)
the point
p
and
TN
its
The
tensor product
TM
@7,M
is
isomorphic to Lin(~~,~~), the
vector space of the linear operators on
7,M,
via
the
canonical
isomorphism
given by
1:
a@X
E
TM
@7,M
4
Z(cr@X)
2=
L,&x
E
Lin(7,M,7pM),
where
La@x
is
the linear map
L,ax
:
Y
E
7,M
-+
L,,x(Y)
=
CU(Y)X
E
7,M
I
§Albert Einstein was born in Ulm, Germany in 1879 and died at Princeton in 1955. He
spent his youth in Munich and after
a
period past in Milan, he moved,
in
1896,
to Swiss.
He obtained his Ph.D.
at
Zurich Polytechnic in 1905. After working at Swiss Patent Office,
he
was
appointed associate professor at Zurich University in 1909 and then at Berlin Uni-
versity in 1913.
He wrote in 1905 six papers. The first of them, with the introduction
of
the photon, gave
a
basic contribution to the rise
of
quantum theory; the second and the
third gave rise to special relativity and, with this, to the new concept of spacetime; the
others explained the Brownian motion and, with this, introduced new methods
to
memure
the dimensions of atoms. His paper on general relativity
is
dated 1915. He was appointed
a
Nobel Prize,
for
the photoelectric effect, in 1921. In 1933, with the introduction
of
racial
Nazis laws, he moved to Princeton where he was appointed to a chair of professor
of
physics
at
The
Institute
for
Advanced Studies, where he taught until 1955.

Endomorphisms
Associated with
a
Mixed
Tensor
Field
191
Then, with the tensor
(6.431,
we
can associate the endomorphism
T
on
7,JM
defined
as
follows
(6.44)
Moreover, there
is
another ~somorphism between the tensor product
TJh/i
@
7,M
and the space Lin(T,M,
7,M)
that associates to every
a
@
X
E
TM
@
7,M
the linear
map
L:,,
:
p
E
TM
-+
~~,~(~)
=
@(p)a
E
TM.
Thus, with the tensor
(6.43),
we can associate also the endomorphi~m
'f'
on
TM
defined by
n
n
i,j=l
k=l
By
using
Eqs.
(6.44)
and
(6.45)'
we
find that
(Pa,X)
=
(cL!,?~).
In
fact,
(6.45)
Henceforth, when
no
confusion possibly arises, we will not distin~ish be-
tween
a
tensor
T
and its associated endomorphisms
T
and
f+.

192
Daflerential
Forms
6.4.1
If
S
and
T
are the endomorphisms associated with two tensor fields of
(1.1)-
type,
and
if
X,
Y
are two arbitrary vector fields, the relation
The
~ijenh~~3
bracket
of
two
mixed
tensor
field3
23c$(X,
Y)
=
[SX,
TYJ
i-
[TX,
SY]
i-
ST[X,
Y]
+
TSIX,
Y]
-
S[X,
TYJ
-
S[TX,
Yj
-
T(X,
SY]
-
T[SX,
Y)
is
called the
Nz~enhuis bracket
of
S
and
T.
It defines
a
vector field
'?fp(X,Y)
which is antisymmetric under the interchange
X
t)
Y.
The (1,2)-type tensor field defined
by
is called the
Nijenhuis torsion
of
S
and
T.
Let
us
observe that
%$(X,
Y)
can also be written in the
form
31$(X,
Y)
=
-(LsxT
+
LTXS
-
SLxT
-
TLxS)Y.
1
2
The
~zjenhu2s tors~on
N;.
of
a
mixed tensor field
T
with itself is called the
Nijenhuis torsion
of
T;
it, generally, is not vanishing.
In such
a
case, the previous relations become
NT(~,
X,
Y)
=
(a,
%T(X,
Y)f
with
Exercise
6.4.2
~~enhuzs torsion. Thus,
it
sa~isfies the conditzo~
Let
us
suppose that the tensor field
(6.43)
has
a
vanishing
(6.46)
From
this relation,
it
follows
that
if
T
is
znvar2an~ for
a
vector field
A,
it
is
~~~arian~
for
all vector fields
TnA,
generated by repeated app~~catzo~
of
T
to
A.
Show that
[TnA, TmA]
=
0
Vn,
m.
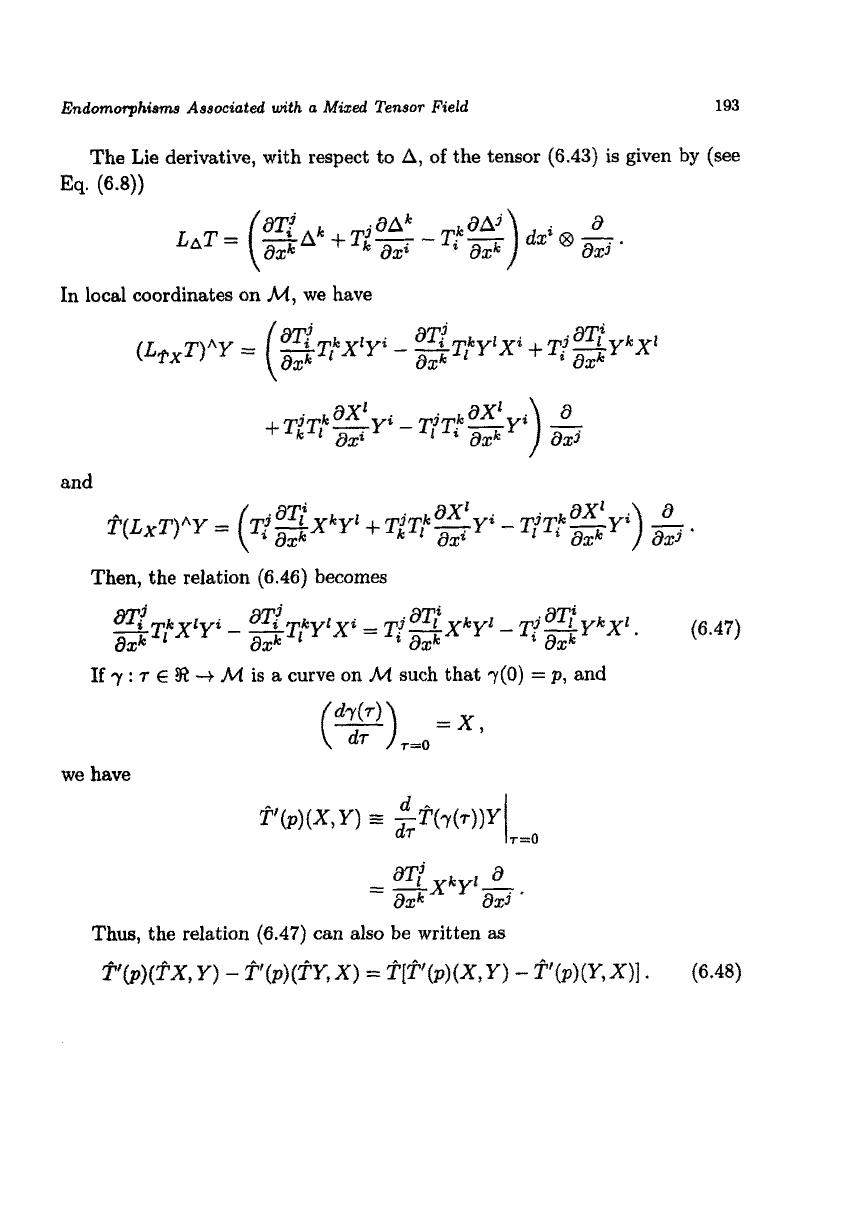
Endomorphisms
Associated
with
a
Mixed
Tensor
Field
193
The Lie derivative, with respect
to
A,
of
the tensor
(6.43)
is
given
by
(see
Eq.
(6.8))
In local coordinates on
M,
we have
and
Then,
the relation
(6.46)
becomes
If
7
:
T
E
R
+
M
is
a
curve on
M
such
that
~(0)
=
p,
and
we have
Thus,
the relation
(6.47)
can also
be
written
as
~'~)(~~,
Y)
-
~~~)~~Y,
X)
=
p[?'(p)(X,
Y)
-
~~)(Y,
X)]
.
(6.48)
