Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


144
Manifolds
and
Tangent
Spaces
The fibers need not be related to the differential structure
of
the base
manifold
M,
In
elementary particle physics,
bundles are considered, whose
fibers are isospin spaces attached
to
points in the space-time, which is the base
manifold. Such a bundle will describe, besides the coordinates
(t,
2,
y,
z),
also
the isospin of an elementary particle.
5.9
General Definition
of
Fiber Bundle
Let
E,
M,
F
be differential manifolds and
n
a differentiable map
r:E+M
from
E
to
M.
are compatible charts' domains
Let
{Uj}j=l,...,,
be a covering of
M,
made
of
open subsets of
M,
which
n
j=l
Let us suppose that,
for
every open set
Uj,
there is a homeomorphism
'pj
from
n-'(Uj)
to the Cartesian product
Uj
x
F
of the form
'Pj
:
Y
E
X-'(uj>
-+
'P~(Y)
=
x(Y),
Gj
(Y)
E
uj
x
F,
A
0
A
A
where
'Pj:
n-'(Uj)
+
F
and the restriction
'Pj
1=-1(~)
of
'Pj
to
n-'(p),
A
+jl =-1(P)
=
-
'Pj,p:
T-'(P)
+
F
is
a
homeomorphism of
n-'(p)
onto
F,
such that the diagram
T-1
(Uj)
xd
L
Pj
Uj
.P
Uj
x
F
commutes; i.e.
T=P0'Pj,
p
denoting the canonical projection from
Uj
x
F
onto
Uj.

General Definition
of
Fiber Bundle
145
A
A-1
Of course, the set
of
maps
'Pk,p
o
'Pj,,:
F
+
F
for all
p
E
Uj
nUk
and for
all
j,
k
E
{
1,
.
,
.
,
n} is
a
group
G
in a natural way.
If
this group
is
a Lie group
and the maps
are differentiable, we will say that
(E,
M,
T,
F,
G)
is
a
differentiable fiber bun-
dle;
M
is
called the
base
of the
bundle,
F
is called
the typical fiber,
and
T-~
(p)
is
called
the
fiber
in
p.
The group is called
the
structure group.
Usually the
bundle
(E,
M,
T,
F,
G)
is
simply indicated by
E.
Locally,
a
fiber bundle is always a Cartesian product; i.e.,
T-~
(Uj)
5
Uj
x
F.
A
fiber bundle
E,
which is
globally
a Cartesian product; that
is,
if
E
=
M
x
F,
is called
trivial.
For more details see
RRf.
19.
5.9.1
Let
us
consider again an n-dimensional differential manifold
M
and the set
of the
pairs
(p,X,)
where
p
E
M
and
X,
E
7,M.
Such a set, denoted by
the symbol
TM,
can be provided of
a
differential bundle structure in the
following way:
as
a base we take the differential manifold
M
and the map
A
is the projection
More
on the tangent bundle
T
:
(p,X,)
E
7M
+n(p,X,)
=p
E
M.
The typical fiber
F
is the Euclidean space
IR",
and for every
p
E
M,
the
fiber
~-l(p)
is
7,M,
the tangent space
to
M
at
p.
The covering of
M
is
made
by the domains
Uj
of compatible charts
(Uj, $j)
such that
n
M
=
UUj.
j=l
The homeomorphisms
'pj
are defined
as
follows:
'Pj: (P,xp)~~-l(Uj)
-,'pj(~,Xp)=(~(pi~p),(~j)*p(~2(~,~p)))
~ujx~~,
where
r&,
X,)
=
X,.
The coordinates of the point
(p,
X,)
in
TM
are then
1
(z'
,
.
.
.
,
zn,
x,
,
. .
.
,
X,")
,

146
Manifolds and Tangent
Spaces
where
zi
are the coordinates
of
p
and
are the coordinates
of
Xp
in the chart
(Uj,
$j).
The linear map
is an isomorphism between the spaces
7,M
and
32”.
If
p
is representable on two charts
(Uj,
$j)
and
(Uk,
$k),
the map
is
an isomorphism
of
%”
onto itself. Thus, the structure group
G
is
GL(n,
8).
As
we have already noted, the space
7M
is usually called the tangent
bundle.
The cotangent bundle
The cotangent bundle is built exactly
as
the tangent bundle
TM,
by simply
replacing the tangent spaces
7,M
with the cotangent spaces
TM.
5.9.2
The tangent bundle
75‘
of the circle
S’
can be visualized as
a
cylinder, which
globally
is
the Cartesian product
S1
x
8,
and
so
it is
a
trivial bundle.
A
cylinder, once cut along a directrix, “becomes” an infinite rectangle be-
longing to
%’;
a
part
of
it
is
a
finite rectangle.
Let
a
and
a’
be the upper corners
of
the rectangle and
b
and
b’
the down
ones. Before the cut,
a
-
a’
was
identified with the same point
of
the cylinder
and
a’
-
b’
with a different point along the same directrix.
Thus, by gluing
a
with
a’
and
b
with
b’,
we obtain an upper- and down-
bounded part of the cylinder, while by gluing
a
with
b‘
and
b
with
a’,
we obtain
the so-called
Mobius band.
Then, with the same base space
S‘
and the same fibers
R,
we can build
two globally different bundles. The first,
7S’,
is
a
trivial bundle, the second,
Analysis
of
two
bundles
with
S’
as base
manifold

Geneml Definition
of
Fiber Bundle
147
a nontrivial one; both show the same local properties. Their difference, which
is of global type, is described by the
structure group.
The bundle
7-27'
Let
(l4j)j-l
,...,
be an open covering of,
S'
=
U,"=,Uj.
Every
Uj
has,
as
coordinate system,
a
parameter
rj
along
S1,
and for
p
E
Uj,
a basis of
7pS1
c"
F
=
92
will be given by the vector
d/drj.
Thus, a given vector
V
E
7pS1
will
be represented by
vjdldrj,
where
vj
is
a
real number, and since
j
is fixed,
there is no
sum
over
j.
If
p
belongs to the intersection of two neighborhoods
Uj
and
Ui,
the vector
V
will have two representations,
vjdldrj
and
vid/dri,
where since
r,
and
rj
are unrelated,
vj
and
vi
are two nonzero real numbers.
o
Vj,p:
!R
-+
!R
maps
vj
in
d,
so
that it reduces simply
to
the multiplication by the real number
Thus, the structure group of
TS',
since
rjj
are nonzero arbitrary real num-
bers, is GL(1,R)
3
(92
-
{0},
x);
that is,
92
-
(0)
with the composition
law
given by the multiplication.
We observe now that, for any
j,
the parameters
rj
can be chosen to be
concordant;
that is, in such a
way
that any two of them, namely
rj
and
rj,
increase in the same direction of
S1
(drildrj
>
0),
in the intersection
Uj
nui.
With this choice,
rjj
>
0
and the structure group reduces to
R+,
the positive
real numbers with the composition law given by the multiplication.
Moreover, the Jacobians
drildrj
could be chosen in such a way that, in the
intersection
Uj
n
Ui,
we have
drildrj
=
1.
Thus, the structure group reduces,
finally,
to
(1,
x),
a
trivial group
&s
trivial
as
the bundle
7s'.
A
A-1
Since the typical fiber is
92,
the homeomorphism
rij
=
v'/vj.
The
Mobius
fiber
bundle
It
is
easy
to
see that the Mobius strip is not an orientable manifold,
so
that at
least one of the real numbers
rij
=
vi/d
will be
-1.
In this way, the structure
group reduces to
((1,
-l},
x).
The bundle
of
frames and the principal fiber bundle
The
frame bundle
FTM
of an n-dimensional differential manifold
M
is a bundle
having
M
as
base space, GL(n,
R)
as
structure group (the same of the tangent

148
Manifolds and Tangent Spaces
bundle
TM),
and the set of all bases of
R"
as
fiber. Since the set of all bases
of
92''
is homeomorphic to
GL(n,
R),
the typical fiber
F
is just
GL(n,
R).
Then
7M
has
G
=
GL(n,
FR)
and
F
=
R",
while
FrM
has
G
=
GL(n,
R)
and
F
=
GL(n,
R).
The frame bundle
FrM
is just an example of
a
bundle in which the struc-
ture group (not necessarily
GL(n,R))
is homeomorphic to the fiber. Such
a
bundle, that is,
a
bundle in which the structure group
is
homeomorphic to the
fiber, is called
a
princzpal fiber bundle.
5.10
Integral Curves
of
a
Vector Field
As
it has already been said, given
a
vector
X,
E
7,M,
there exist infinitely
many differentiable curves on
M
which in
p
admit
X,
as
tangent vector. Given
two vectors,
X,
and
X,,
it is also easy to find curves on
M
admitting
X,
and
X,
as
tangent vectors at
p
and
q,
respectively. It is also clear that the search
for such curves becomes more and more difficult as the number of the given
vectors increases. It is in a sense surprising that, given
a
vector field
X
on
M)
and then the assignment of infinitely many tangent vectors (one in each tangent
space
7,M,
Vp
E
M),
there exists always
a
curve
p
=
~(T),T
~]a,b[C
112
on
M,
whose tangent vector in
a
point
po
=
TO)
coincides with the value
Xp0
of
the field at the point,
VTO
€]a,
b[.
As
a matter of the fact, if
xi
=
xi(.)
is the local parametric represen-
tation of the unknown curve, the derivatives
dxi/dT(,=,
will represent the
components of the tangent vector at
TO,
while, if
X
=
Xi(a/axi)
is the local
representation of the vector field,
Xi(p0)
will be the components of the vector
corresponding to the value of the vector field
X
at
PO.
Thus, the unknown
curve will be the solution of the system of differential equations
dxi
-
=
xi(xC),
dr
~i
E
(1~2,.
.
.
,n).
We know that, for
smooth
Xi,
the above system always admits, locally,
a
unique solution
xi
=
z~(T),
assuming at
T
=
TO
a
prefixed value
xb.
Such
a
solution is called an
integral curve
of
the vector
field
X.
Such curves are well known in physics
as
force lines,
a
name given by
M.
Faraday who introduced them for the electric and magnetic vector fields
E
and
H.

Zntegml
Curues
of
a
Vector
Field
Example
19
Let
149
be the harmonic oscallator vector field. Its integral curves will be given by so-
lutions
of
the differential system
which
are
circles
x2
+
y2
=
r2
of
arbitrary radius
r.
Example
20
The integral curves
of
the vector field
Ya
xa
x=(x+-)--(Y+;)z,
T
aY
where
r
=
(x2
+
y2)If2, will be given by the solutions
of
the differential system
dx
-=-(y+j),
-
=
(x++)
.
By multiplying the first equation by x and the second
by
y,
we obtain
y-= yx+$
dr
Thus,
Id
2
dr
-
-(X2
-k
y2)
=
T
,
OT

150
which gives
~an~~o~ds and Tangent
Spaces
r=~+c,
represents infinitely many spirals,
one
for
each value
of
the constant
c.
We can summarize saying that, for every point
p
in
M
there exists an
integral curve
of
X;
i.e. a curve on
M
which satisfies the differential equations
More
precisely, for every
p
E
N,
there exists an interval
I$,
c
!R
and an
integral curve
T
E
I,
-+
y(7,p)
of class
ChS'
in
Ip,
such that
y(0,p)
=
p.
Moreover, this integral curve is uniquely determined.
It
follows that,
if
(T
and
T
are elements of
Ip
such that
CT
+
T
E
Ip,
we have
y(r1y(0,p))
=Y(T$-C,P),
VPEM.
(5.11)
If
po
E
M,
there exist
an
open set
U(p0)
C
M
containing
p0
and
an
interval
Im
c
8
such
that
y
is
defined on
Ipo
x
U(p0)
Y
:
(T,P)
E
I,,
x
WPOt
+
T'fT,PI
E
M
-
For
every
T
E
I$,,
,
the map
YT
:
P
U(P0)
-+
YW
=
Y(7,P)
E
M
(5.12)
is
a diffeornorphism between open subsets of
M;
a point
p
in
U(p0)
goes to
a
point
~'(p)
E
M
aIong the integral curve of
X
at
p.
The position of
yr(p)
is
determined by
T.
Let
{U(po>}
be
a
covering
of
M.
The intersection
I
of
the intervals
I,,
corresponding
to
the open sets
U(p0)
can be empty, but if the manifold
N
is
compact, the covering
(U(p0))
contains
a
finite subcovering and the intersec-
tion
I
of
the corresponding intervals is certainly not empty.
In
such
a
case the
diff~morphis~
(5.12)
can be extended to the entire manifold
M,
with
T
E
I
and the vector field
X
said to be
complete,29
F'rom
Eq.
(5.11), we have
r(7
+
g,
PI
=
Y'+"(P)
7
$7,
r(0,
PI>
=
YT(Y(O,
P))
=
rr
0
Y"(P)
>

The
Lie
Derivative
151
and then
pff
=
77
0
yo.
Moreover, every
rT
is supplied
by
an inverse; that is by the diffeomorphism
What has been said above can be summarized by the following theorem.2g
Theorem
21
With eueq
Ch
d~fferentia~ze vector field X(p), on a
Ck
(h
I
k
-
I)
compact, differential manifold
M,
a one parameter
group
is
associated
y‘:M-+M.
(5.13)
yMT,
so
that we can define
yT
for every
T
E
8.
This
grou~
of
~~~eo~o~his~s
of
M
in
itse2f is
sack
t~a~
The group
rT
is also called the
Bow
of
the vector field
X(p),
and
it
is also
denoted by
7:.
The group
(5.13)
is
then well defined if the manifold
M
is compact. In the
general case, the
y7
are defined just like in
Eq.
(5.12)
only in neighborhoods
of a point
po
E
M
and for small
T.
5.11
The
Lie
Derivative
Let
X(p)
and
Y(p)
be two vector fields on an n-dimensional differential man-
ifold
M,
and
y;;
be the flow of the vector field
X.
The Lie derivative
LxY
of
the vector field
Y
is
the vector field defined by
the relation
where
(5.14)
(rj-T)*~T(,~
:
~T(~)M
+
T,M
Let
us
calculate the Lie derivative
of
the
basis
vectors
{afax:”}.
In order to simplify the notation, let
us
indicate with
z
E
8%
the coordinates
of
the points of
M
and let
us
set
f(s)
=
y.
If
#(T,
Z)
are the coordinates
of
rjT(x),
and
~(T,z)
those of
4-T(y),
then
@(O,p)
=
zi
and
#(O,y)
=
yz.
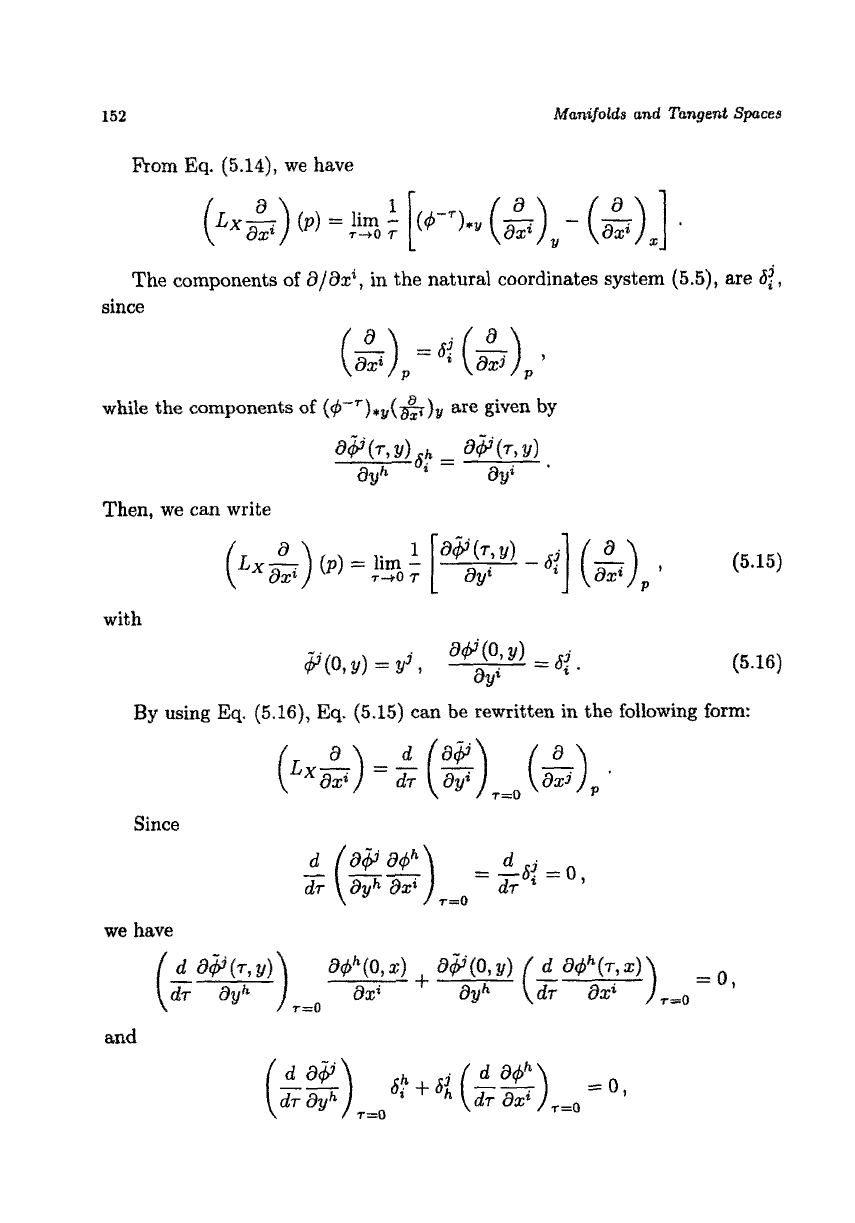
152
~a~af~~ds
and
Tangent
Spaces
From
Eq.
(5.14),
we have
The components
of
a/azi,
in
the natural coordinates system
(5.5),
are
$,
since
(&)p=Ji($)
'
P
while the components
of
{~-~)*~(~)~
are
given
by
Then, we can write
By
using
Eq.
(5.161,
Eq.
(5.15)
can be rewritten in the following
fonn:
Since
we
have
and

The
Lie
Derivative
so
that
153
and
a')
&Ip
=
-%
(&)
.
(5.17)
r=O
P
The Lie derivative is an additive operator; i.e.
Lx(U
+
V)
=
LXU
+
LXV,
where
X,
U,
and
V
are vector fields on the manifold
M.
Moreover, it satisfies
the
Leibnitz
rule
Lx(U
@V)
=
(LXU)
@V
+
U@
LXV,
where the symbol
@
denotes the
tensor product
defined in the next chapter.
the
Lie
derivative
Lxdxi
of the basis
differential
1-forms
{dx'}.
Indeed
By
using the
Eq.
(5.17)
and the relations
(dx', a/axj)
=
dj,
we can calculate
Lx
(
dx'&)
=
Lxd;
=
0,
so
that
(
Lxdxi,
&)
=
-
(
dzi, Lx
&)
=
(
dx',
64
axk
gp)
a
=
(
-dxk,
axi
-)
a
=
(dX',
s)
.
ask
axj
Therefore,
we
obtain
Lxdx'
=
dXi
.
