Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support
Подождите немного. Документ загружается.


116 4 Sensitivity, Specificity, and Relatives
In the parallel strategy the combination is positive if at least one test is
positive and negative if all tests are negative. Then the sensitivity is calcu-
lated as the probability of a union and the specificity as the probability of an
intersection:
Parallel combination (Positive if at least 1 positive)
Se =1 −
[
(1
−Se
1
) ×(1 −Se
2
) ×···×(1 −Se
k
)
]
Sp
=Sp
1
×Sp
2
×···×Sp
k
It is easy to see that in the parallel strategy the sensitivity is larger than any
individual sensitivity and the specificity smaller than any individual speci-
ficity.
In the serial strategy, the combination is positive if all tests are positive
and negative if at least one test is negative. Then the sensitivity is calculated
as the probability of an intersection and the specificity as the probability of a
union:
Serial combination (Positive if all positive)
Se =Se
1
×Se
2
×···×Se
k
Sp =1 −
£
(1 −Sp
1
) ×(1 −Sp
2
) ×···×(1 −Sp
k
)
¤
Here, the overall sensitivity is smaller than any individual sensitivity, while
the specificity is larger than any individual specificity.
There are other possible combinations as well as procedures that address
bias and correlation among the individual tests.
Example 4.3. Combining Two Tests for Sarcoidosis. Parikh et al. (2008)
provide an example of combining two tests for sarcoidosis. Sarcoidosis is an id-
iopathic multisystem granulomatous disease, where the diagnosis is made by
a combination of clinical, radiological, and laboratory findings. The gold stan-
dard is a tissue biopsy showing noncaseating granuloma. Ocular sarcoidosis
could present as anterior, intermediate, posterior, or panuveitis; but none of
these is pathognomonic. Therefore, one has to rely on ancillary testing to con-
firm the diagnosis.
An angiotensin-converting enzyme (ACE) test has a sensitivity of 73% and
a specificity of 83% to diagnose sarcoidosis. An abnormal gallium scan has a
sensitivity of 91% and a specificity of 84%. Though individually the specificity
of either test is not impressive, for the serial combination the specificity be-
comes
Sp
=1 −(1 −0.84) ×(1 −0.83) =1 −(0.16 ×0.17) =0.97.
The combination sensitivity becomes 0.73
×0.91 = 0.66. Note that the overall
specificity drastically improves, but at the expense of overall sensitivity.
The independence of tests in the previous example is a quite limiting as-
sumption. One may argue that two tests for the same disease are seldom in-
dependent by the very nature of the testing problem.

4.3 Combining Two or More Tests 117
In the following example, we show how to handle more complex batteries of
tests in which the tests could be dependent. The example considers two tests
and a parallel combination strategy, but it could be extended to any number of
tests and to more general combination strategies.
The approach is based on simulation since analytic solutions are typically
computationally involved.
Example 4.4. Simulation Approach. Suppose a testing procedure consists
of two tests given in a sequence. Test A has a sensitivity of 0.9 and a specificity
of 0.8. Test B has a sensitivity of 0.7 and a specificity of 0.9 for subjects who
tested negative in test A and a sensitivity of 0.95 and a specificity of 0.6 for
subjects who tested positive in test A.
Clearly, test A and test B are dependent. If a subject is declared positive
when the result of at least one of the two tests was positive (parallel link),
what is the overall sensitivity/specificity of the described testing procedure?
The population prevalence is considered known and is used in the simulation
of a patient’s status, but it does not affect the overall sensitivity/specificity.
Note that if a subject’s status
s is equal to 0/1 when the disease is ab-
sent/present, then the result of a test is
s
*
(rand < se) + (1-s)
*
(rand > sp)
for a known sensitivity and specificity, se, sp. The test outcome is binary, with
0/1 denoting a negative/positive test result.
The following MATLAB code (
simulatetesting2.m) considers 20,000
subjects from a population where the disease prevalence is 0.2. The estimated
sensitivity/specificity was 0.97/0.72, but simulation results may vary slightly
due to the random status of subjects.
nsubjects = 20000;
prevalence = 0.2;
se1 =0.9; sp1 = 0.8; %se/sp of test1
se20 =0.7; sp20 = 0.9; %se/sp of test2 if test1=0
se21 =0.95; sp21 = 0.6; %se/sp of test2 if test1=1
tests = [];
ss=[]; tp=0; fp=0; fn=0; tn=0;
for i = 1:nsubjects
%simulate a subject wp of disease equal to prevalence
s = (rand < prevalence);
%test the subject
test1=s
*
(rand < se1) + (1-s)
*
(rand>sp1); %test is 0 or 1
if (test1 == 0)
test2=s
*
(rand < se20) + (1-s)
*
(rand>sp20);
else
test2=s
*
(rand < se21) + (1-s)
*
(rand>sp21);
end
%test = test1
*
test2; %for serial
test = (test1 + test2 > 0); %for parallel
ss=[ss s]; %save subject’s status
tests = [tests test]; %save subject’s test
%building the test table

118 4 Sensitivity, Specificity, and Relatives
tp = tp + test
*
s; %true positives
fp = fp + test
*
(1-s); %false positives
fn = fn + (1-test)
*
s; %false negatives
tn = tn + (1-test)
*
(1-s); %true negatives
end
% estimate overall Se/Sp from the table
sens = tp/(tp+fn)
spec = tn/(tn+fp)
Remark: In the previous discussion we assumed that a true disease status
was known and that a perfect gold standard test was available. In many cases
an error-free assessment does not exist but a reference test, with known sen-
sitivity Se
R
and specificity S p
R
, could be used. By taking this reference test
as a gold standard and by not accounting for its errors would lead to biases in
evaluating a new test. Staquet et al. (1981) provide a solution based on Se
R
,
S p
R
, and concordance of results between the two tests.
Another approach approach to this problem is “discrepant resolution,” in
which the subjects for whom the reference and new test disagreed were sub-
jected to a third “resolver” test. Although commonly used, the resolver method
can be biased and can overestimate sensitivity and specificity of a new test
significantly (Hawkins et al., 2001; Qu and Hadgu, 1998).
4.4 ROC Curves
The receiver operating characteristic (ROC) curve was first used during World
War II for the analysis of radar signals before it was employed in signal de-
tection theory and, subsequently, in a range of fields where testing is critical.
It is defined as a graphical plot of
sensitivity vs. (1 - specificity) for a bi-
nary classifier system as its discrimination threshold (value that separates
positives and negatives) varies.
Let us look at an ROC curve using the D-dimer example from the pre-
vious section. Mavromatis and Kessler (2001) report that in 18 publications
(between 1988 and 1998) concerning D-dimer testing, the reported cut point
for declaring the test positive ranged from 250 to 1000 ng/mL. What cut point
should be recommended? To increase the apparently low specificity in the pre-
vious D-dimer analysis, suppose that the threshold for testing positive is in-
creased from 500 to 650 ng/mL and that the data are distributed in the follow-
ing way:
Acute PE No PE present Total
Test positive (D-dimer ≥ 650 ng/mL) 31 33 64
Test negative (D-dimer < 650 ng/mL) 14 95 109
Total 45 128 173
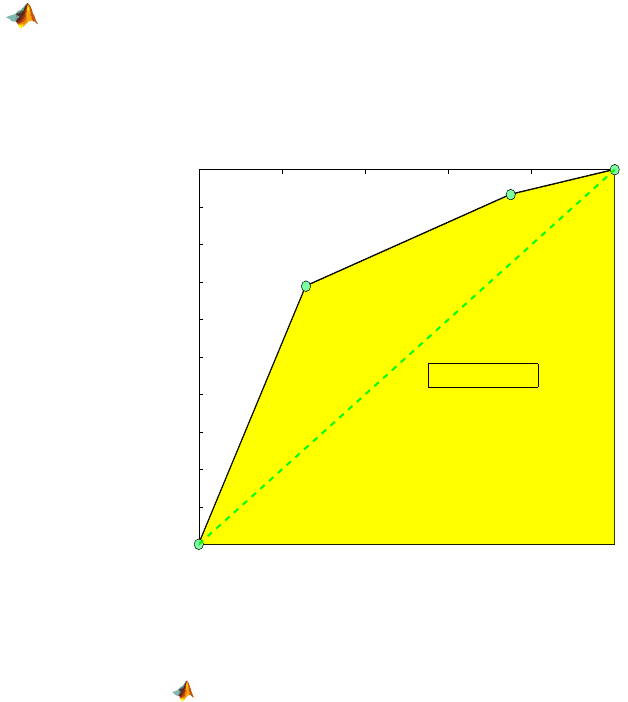
4.4 ROC Curves 119
This new table results in the following sesp output:
[a b c d e f] = sesp(31,33,14,95);
Se Sp Pre PPV NPV LRP Ag Yi
0.6889 0.7422 0.2601 0.4844 0.8716 2.6721 0.7283 0.3048
Combining this with the output of the 500-ng/mL threshold, we get the
vectors
1-sp = [0 1-0.7422 1-0.25 1] and se = [0 0.6889 0.9333 1].
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Sensitivity
1−Specificity
(0.2578, 0.6889)
(0.75, 0.9333)
Area = 0.7297
Fig. 4.1 Rudimentary ROC curve for D-dimer data based on two thresholds.
The code RocDdimer.m plots this “rudimentary” ROC curve (Fig. 4.1).
The curve is rudimentary since it is based on only two tests. Note that points
(0,0) and (1,1) always belong to ROC curves. These two points correspond to
the trivial tests in which all patients test negative or all patients test posi-
tive. The area under the ROC curve (AUC), is a well-accepted measure of test
performance. The closer the area is to 1, the more unbalanced the ROC curve,
implying that both sensitivity and specificity of the test are high. It is inter-
esting that some researchers assign an academic scale to AUC as an informal
measure of test performance.

120 4 Sensitivity, Specificity, and Relatives
AUC Performance
0.9–1.0 A
0.8–0.9 B
0.7–0.8 C
0.6–0.7 D
0.0–0.6 F
The following MATLAB program calculates AUC when the vectors csp = 1
- specificity
and sensitivity are supplied.
function A = auc(csp, se)
%
% A = auc(csp,se) computes the area under the ROC curve
% where ’csp’ and ’se’ are vectors representing (1-specificity)
% and (sensitivity), used to plot the ROC curve
% The length of the vectors has to be the same
csp=csp(:); se = se(:);
if length(csp) ~= length(se)
error(’Input vectors (1-specificity) ...
and (sensitivity) should have the same length’)
end
A = sum((csp(2:end)-csp(1:end-1)) .
*
(se(2:end)+se(1:end-1))/2 );
For example, the AUC for the D-dimer ROC based on the two thresholds is
approx. 73%, a grade of C:
auc([0, 1-0.7422, 1-0.25, 1],[0 0.6889 0.9333 1])
ans = 0.7297
To choose the best test out of a multiplicity of tests obtained by changing
the threshold and generating the ROC curve, select the test corresponding to
the point in the ROC curve most distant from the diagonal. This point corre-
sponds to a Youden index
Y I
= max
i
Se
i
+Sp
i
−1
p
2
,
where Se
i
and Sp
i
are, respectively, the sensitivity and specificity for the ith
test. Thus, the Youden index is the distance of the most distant point (1
−
Sp,Se) on the ROC curve from the diagonal. It ranges between 0 and
p
2/2.
In the D-dimer example, the Youden index for the test with a 500-ng/mL
threshold is 0.1296, compared to 0.3048 for the test with a 650-ng/mL thresh-
old. Between the two tests, the test with the 650-ng/mL threshold is preferred.
Example 4.5. ADA. Adenosine deaminase (ADA) is an enzyme involved in the
breakdown of adenosine to uric acid. ADA levels were found to be elevated in
the pleural fluid of patients with tuberculosis (TB) pleural effusion. Pleural
effusion is a very common clinical problem. It may occur in patients of pul-
monary TB, pneumonia, malignancy, congestive cardiac failure, cirrhosis of

4.4 ROC Curves 121
the liver, nephrotic syndrome, pulmonary infarction, and connective tissue dis-
orders. TB is one of the primary causes of pleural effusion. Numerous studies
have evaluated the usefulness of ADA estimation in the diagnosis of TB pleu-
ral effusion. However, the sensitivity and specificity of ADA estimation and
the cutoff level used for distinguishing TB pleural effusion from non-TB pleu-
ral effusion have varied between studies. The data (given in
ROCTBCA.XLS
or ROC.mat) were collected by Dr. Mark Hopley of Chris-Hani Baragwanath
Hospital (CHB, the largest hospital in the world), with the goal of critically
evaluating the sensitivity and specificity of ADA estimation in the diagnosis
of TB pleural effusion.
The data set consists of three columns:
Column 1 contains ADA levels.
Column 2 is an indicator of TB. The indicator is “1” if the patient had
documented TB, zero otherwise.
Column 3 is an indicator of documented carcinoma. Six patients who had
both carcinoma and TB have been excluded from the analysis.
To create an empirical ROC curve, the following four steps are applied:
(i) The data are sorted according to the ADA level, with the largest values
first.
(ii) A column is created where each entry gives the total number of TB
patients with ADA levels greater than or equal to the ADA value for that
entry.
(iii) A column equivalent to that from step 2 is created for patients with
cancer.
(iv) Two new columns are created, containing the true positive frequency
(TPF) and false positive frequency (FPF) for each entry. The TPF is calculated
by taking the number of TB cases identified at or above the ADA level for
the current entry and dividing by the total number of TB cases. The FPF is
determined by taking the number of “false TB alarms” (cancer patients) at or
above that level and dividing by the total number of such non-TB patients.
This description can be simply coded in MATLAB thanks to the cumulative
summation (
cumsum) command:
disp(’ROC Curve Example’)
set(0, ’DefaultAxesFontSize’, 16);
fs = 15;
% data file ADA.mat should be on path
load ’ADA.mat’
% columns in ADA.mat are:
% 1. ADA level (ordered decreasingly)
% 2. indicator of case TB
% 3. indicator of non-case CA
cumultruepos = cumsum(ada(:,2));
cumulfalsepos = cumsum(ada(:,3));
% these are true positives/false positives if the
% cut-level is from the sequence ada(:,1).
tpf = cumultruepos/cumultruepos(end); %sensitivity
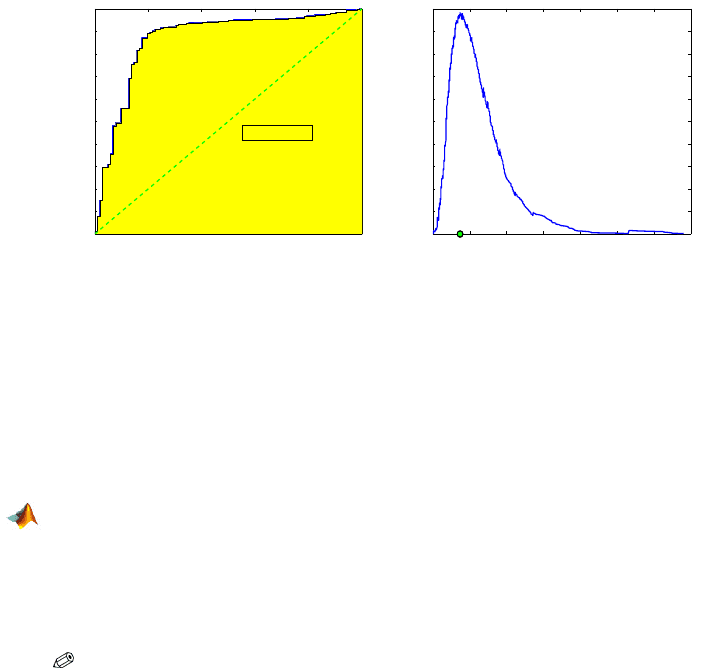
122 4 Sensitivity, Specificity, and Relatives
fpf = cumulfalsepos/cumulfalsepos(end); %1-specificity
plot(fpf,tpf) %ROC, sensitivity against (1-specificity)
xlabel(’1 - specificity’)
ylabel(’sensitivity’)
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1 − specificity
sensitivity
Area = 0.8646
0 50 100 150 200 250 300 350
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
37
ADA level
Youden index
(a) (b)
Fig. 4.2 (a) ROC Curve for ADA data. (b) Youden index against ADA level.
Which ADA level should be recommended as a threshold? The Youden in-
dex for the ROC curve in Fig. 4.2a is 0.4910, which corresponds to ADA level of
37, Fig. 4.2b. For this particular threshold, the sensitivity and specificity are
0.8904 and 0.8039, respectively.
%youden index
yi = max((seth-cspth)/sqrt(2)) %0.4910
%ADA level corresponding to YI
ada((seth-cspth)/sqrt(2)== yi , 1) %37
% sensitivity/specificity at YI
seth((seth-cspth)/sqrt(2)== yi) %0.8904
1 - cspth((seth-cspth)/sqrt(2)== yi) %0.8039
4.5 Exercises
4.1. Stacked Auditory Brainstem Response. The failure of standard audi-
tory brainstem response (ABR) measures to detect small (
<1 cm) acoustic
tumors has led to the use of enhanced magnetic resonance imaging (MRI)
as the standard to screen for small tumors. The study by Don et al. (2005)
investigated the suitability of the stacked ABR as a sensitive screening
alternative to MRI for small acoustic tumors (SATs). The objective of the

4.5 Exercises 123
study was to determine the sensitivity and specificity of the stacked ABR
technique for detecting SATs. A total of 54 patients were studied who had
MRI-identified acoustic tumors that were either
<1 cm in size or undetected
by standard ABR methods, irrespective of size. There were 78 nontumor
normal-hearing subjects who tested as controls. The stacked ABR demon-
strated 95% sensitivity and 88% specificity. Recover the testing table.
4.2. Hypothyroidism. Low values of a total thyroxine (T4) test can be indica-
tive of hypothyroidism (Goldstein and Mushlin 1987). Hypothyroidism is
a condition in which the body lacks sufficient thyroid hormone. Since the
main purpose of the thyroid hormone is to “run the body’s metabolism,”
it is understandable that people with this condition will have symptoms
associated with a slow metabolism. Over five million Americans have this
common medical condition.
A total of 195 patients, among which 59 have confirmed hypothyroidism,
have been tested for the level of T4. If the patients with a T4 level
≤5 are
considered positive for hypothyroidism, the following table is obtained:
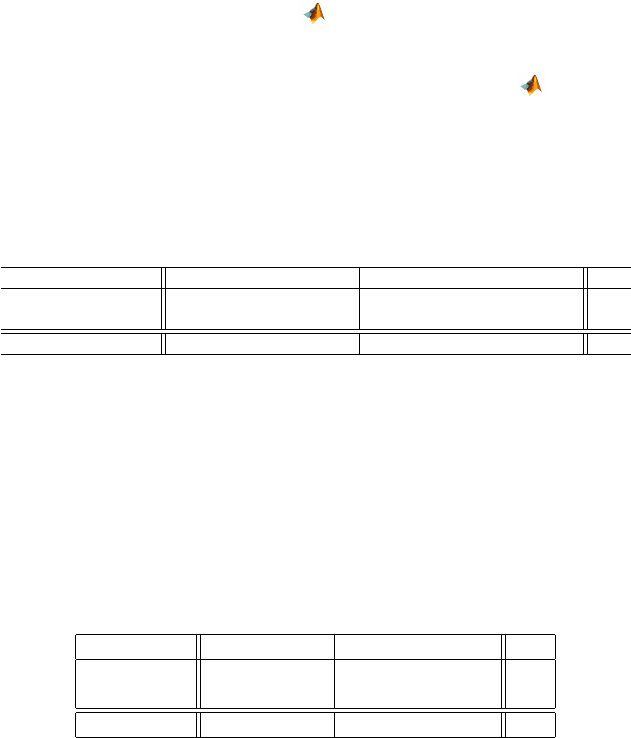
T4 value Hypothyroid Euthyroid Total
Positive, T4 ≤5 35 5 40
Negative, T4 >5 24 131 155
Total 59 136 195
However, if the thresholds for T4 are 6, 7, 8, and 9, the following tables are
obtained.
T4 value Hypothyroid Euthyroid Total
Positive, T4 ≤6 39 10 49
Negative, T4 >6 20 126 146
Total 59 136 195
T4 value Hypothyroid Euthyroid Total
Positive, T4 ≤7 46 29 75
Negative, T4 >7 13 107 120
Total 59 136 195
T4 value Hypothyroid Euthyroid Total
Positive, T4 ≤8 51 61 112
Negative, T4 >8 8 75 83
Total 59 136 195
T4 value Hypothyroid Euthyroid Total
Positive, T4 ≤9 57 96 153
Negative, T4 >9 2 40 42
Total 59 136 195
124 4 Sensitivity, Specificity, and Relatives
Notice that you can improve the sensitivity by moving the threshold to a
higher T4 value; that is, you can make the criterion for a positive test less
strict. You can improve the specificity by moving the threshold to a lower
T4 value; that is, you can make the criterion for a positive test more strict.
Thus, there is a tradeoff between sensitivity and specificity.
(a) For the test that uses T4
=7 as the threshold, find the sensitivity, speci-
ficity, positive and negative predictive values, likelihood ratio, and degree
of agreement. You can use the code
sesp.m.
(b) Using the given thresholds for the test to be positive, plot the ROC curve.
What threshold would you recommend? Explain your choice.
(c) Find the area under the ROC curve. You can use the code
auc.m.
4.3. Alzheimer’s. A medical research team wished to evaluate a proposed
screening test for Alzheimer’s disease. The test was given to a random sam-
ple of 450 patients with Alzheimer’s disease and to an independent sample
of 500 subjects without symptoms of the disease.
The two samples were drawn from a population of subjects who are 65 years
old or older. The results are as follows:
Test result diagnosis Diagnosed Alzheimer’s, D No Alzheimer’s symptoms, D
c
Total
Positive test T 436 5 441
Negative test T
c
14 495 509
Total 450 500 950
(a) Using the numbers from the table, estimate P(T|D) and P(T
c
|D
c
). Inter-
pret these probabilities in terms of the problem.
The probability of D (prevalence) is the rate of the disease in the rele-
vant population (
≥65 y.o.) and is estimated to be 11.3% (Evans 1990). Find
P(D|T) (positive predicted value) using Bayes’ rule. You cannot find P(D|T)
using information from the table only – you need external info.
4.4. Test for Being a Duchenne Muscular Dystrophy Carrier.
In Exercise
2.16 researchers used measures of pyruvate kinase and lactate dehydrogi-
nase to assess an individual’s carrier status. The following table closely
follows the authors’ report.
Woman carrier Woman not carrier Total
Test positive 56 6 62
Test negative 11 121 132
total 67 127 194
(a) Find the sensitivity, specificity, and degree of agreement.
The sample is not representative of the general population for which the
prevalence of carriers is 0.03%, or 3 in 10,000.
(b) With this information, find the PPV of the test, that is, the probability
that a woman is a DMD carrier if she tested positive.
(c) What is the PPV if the table was constructed from a random sample of
194 subjects from a general population?

4.5 Exercises 125
(d) Approximate the probability that among 15,000 women randomly se-
lected from a general population, at least 2 are DMD carriers.
4.5. Parkinson’s Disease Statistical Excursions. Parkinson’s disease or,
“shaking palsy,” is a brain disorder that causes muscle tremor, stiffness,
and weakness. Early symptoms of Parkinson’s disease include muscular
stiffness, a tendency to tire more easily than usual, and trembling that usu-
ally begins with a slight tremor in one hand, arm, or leg. This trembling is
worse when the body is at rest but will generally stop when the body is in
use, for example, when the hand becomes occupied by “pill rolling,” or when
the thumb and forefinger are rubbed together as if rolling a pill (Fig. 4.3).
Fig. 4.3 “Pill rolling” stops muscle tremors in early Parkinson’s disease.
In the later stages of Parkinson’s disease, the affected person loses the abil-
ity to control his or her movements and the intellect begins to decline, mak-
ing everyday activities hard to manage.
In a study by Schipper et al. (2008), 52 subjects, 20 with mild or moderate
stages of Parkinson’s disease and 32 age-matched controls, had whole blood
samples analyzed using the near-infrared (NIR) spectroscopy and Raman
spectroscopy methods. The data showed that the two independent biospec-
troscopy measurement techniques yielded similar and consistent results. In
differentiating Parkinson’s disease patients from the control group, Raman
spectroscopy resulted in eight false positives and four false negatives. NIR
spectroscopy resulted in four false positives and five false negatives.
(a) From the description above, construct tables for NIR spectroscopy and
Raman spectroscopy containing TP, FP, FN and TN.
(b) For both methods find the sensitivity and specificity. Assume that the
prevalence of Parkinson’s disease in the age group matching this group is
1/120 for the general population. For both methods, also find the PPV, that
is, the probability that a person who tested positive and was randomly se-
lected from the same age group in the general population has the disease if
no other clinical information is available.
(c) Mr. Smith is one of the 52 subjects in the study and he tested positive
under a Raman spectroscopy test. What is the probability that Mr. Smith
has the disease?
