Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

742 19 Bayesian Inference Using Gibbs Sampling – BUGS Project

Table 19.2 Built-in distributions with WinBUGS names and their parameterizations.

Distribution WinBUGS code Density

Bernoulli x ∼ dbern(p) p

(1 − p)

1−x

, x =0,1; 0 ≤ p ≤1

Binomial x ∼ dbin(p, n)

(1 − p)

n−x

, x =0,..., n; 0 ≤ p ≤1

Categorical x ∼ dcat(p[]) p[x], x =1,2,.. ., dim(p)

Poisson x ∼ dpois(lambda)

exp{−λ}, x =0, 1,2, .. ., λ >0

Beta x ∼ dbeta(a,b)

B(a,b)

a−1

(1 −x)

b−1

, 0 = x ≤1, a, b >−1

Chi-square x ∼ dchisqr(k)

k/1−1

exp{− x/2}

k/2

Γ(k/2)

, x ≥0, k >0

Double exponential x ∼ ddexp(mu, tau)

exp{−τ|x −µ|}, x ∈ R, τ >0, µ ∈ R

Exponential x ∼ dexp(lambda) λexp{−λx}, x ≥0, λ ≥ 0

Flat x ∼ dflat() constant; not a proper density

Gamma x ∼ dgamma(a, b)

a−1

Γ(a)

exp(− bx), x, a, b >0

Normal x ∼ dnorm(mu, tau)

τ/(2π)exp{−

(x −µ)

}, x,µ ∈ R, τ >0

Pareto x ∼ dpar)alpha,c) αc

−(α+1)

, x > c

Student-t x ∼ dt(mu, tau, k)

Γ((k+1)/2)

Γ(k/2)

kπ

[1 +

(x −µ)

]

−(k+1)/2

, x ∈R, k ≥2

Uniform x ∼ dunif(a, b)

b− a

, a ≤ x ≤ b

Weibull x ∼ dweib(v, lambda) vλx

v−1

exp{−λx

}, x,v,λ > 0,

Multinomial x[] ∼ dmulti(p[], N)

(

= N,0 < p

<1,

Dirichlet p[] ∼ ddirch(alpha[])

Γ(

)

Γ(α

)

−1

, 0 < p

<1,

Multivariate normal x[] ∼ dmnorm(mu[], T[,]) (2π)

−d/2

|T|

1/2

exp{−1/2(x −µ)

T(x −µ)}, x ∈R

Multivariate Student-t x[] ∼ dmt(mu[], T[,], k)

Γ((k+d)/2)

Γ(k/2)

|T|

1/2

d/2

1 +

(x −µ)

T(x −µ)

−(k+d)/2

, x ∈R

, k ≥2

Wishart x[,] ∼ dwish(R[,], k) |R|

k/2

|x|

(k−p−1)/2

exp{−1/2T r(Rx)}

19.4 MATBUGS: A MATLAB Interface to WinBUGS 743

initStruct = struct( ...

’theta’, 100 );

cd(’C:\MyBugs\matbugs\’)

[samples, stats] = matbugs(dataStruct, ...

fullfile(pwd, ’jeremy.txt’), ...

’init’, initStruct, ...

’nChains’, 1, ...

’view’, 0, ...

’nburnin’, 2000, ...

’nsamples’, 50000, ...

’thin’, 1, ...

’monitorParams’, {’theta’}, ...

’Bugdir’, ’C:/Program Files/BUGS’);

baymean = mean(samples.theta)

frmean=mean(dataStruct.scores)

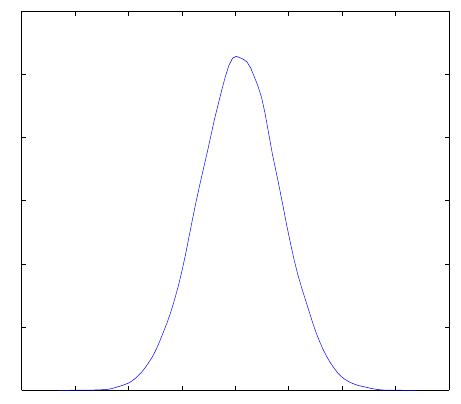
figure(1)

[p, x] = ksdensity(samples.theta);

plot(x, p);

85 90 95 100 105 110 115 120 125

0.02

0.04

0.06

0.08

0.1

0.12

Fig. 19.9 Posterior for Jeremy’s data set. Data are plotted in MATLAB after being exported

from WinBUGS by MATBUGS.

744 19 Bayesian Inference Using Gibbs Sampling – BUGS Project

19.5 Exercises

19.1. A Coin and a Die. The following WinBUGS code simulates ﬂips of a coin.

The outcome H is coded by 1 and T by 0. Mimic this code to simulate rolls

of a fair die.

#coin

model{

flip ~ dcat(p.coin[])

coin <- flip - 1

}

DATA

list(p.coin=c(0.5, 0.5))

#just generate initials

19.2. De Mere Paradox in WinBUGS. In 1654 the Chevalier de Mere asked

Blaise Pascal (1623–1662) the following question: In playing a game with

three dice, why is the sum 11 advantageous to the sum 12 when both are the

result of six possible outcomes? Indeed, there are six favorable triplets for

each of the sums 11 and 12:

11: (1, 4, 6), (1, 5, 5), (2, 3, 6), (2, 4, 5), (3, 3, 5), (3, 4, 4)

12: (1, 5, 6), (2, 4, 6), (2, 5, 5), (3, 3, 6), (3, 4, 5), (4, 4, 4)

19.3. Simulating the Probability of an Interval. Consider an exponen-

tially distributed random variable X , X

∼ E

, with density f (x) =

exp{−x/10}, x > 0. Compute P(10 < X < 16) using (a) exact integration,

(b) MATLAB’s

expcdf, and (c) WinBUGS.

19.4. WinBUGS as a Calculator. WinBUGS can approximate deﬁnite inte-

grals, solve nonlinear equations, and even ﬁnd values of deﬁnite integrals

over random intervals. The following WinBUGS program ﬁnds an approxi-

mation to

sin(x)dx, solves the equation y

−2y =0, and ﬁnds the integral

(1−z

)dz, where R is a beta B e(2, 2) random variable. The solution is

given by the following code:

model{

F(x) <- sin(x)

int <- integral(F(x), 0, pi, 1.0E-6)

pi<- 3.141592659

y0 <- solution(F(y), 1,2, 1.0E-6)

F(y) <- pow(y,5) - 2

zero <- pow(y0, 5)-2

randint <- integral(F(z), 0, randbound, 1.0E-6)

F(z) <- pow(z,3)

(1-pow(z,4))

randbound ~ dbeta(2,2)

}

NO DATA

Chapter References 745

INITS

list(x=1, y=0, z=NA, randbound=0.5)

After model checking, one should go directly to compiling (no data to load

in) and initializing the model. There is NO need to update the model, to

go to the Inference tool, to set the variables for monitoring or to sample.

One simply goes to the Info menu and checks Node Info. In the Node

Info tool one speciﬁes

int for the approximation of an integral, y0 for the

solution of an equation,

zero for checking that y0 satisﬁes the equation

(approximately), and

randint for the value of a random interval.

MATLAB AND WINBUGS FILES AND DATA SETS USED IN THIS CHAPTER

http://springer.bme.gatech.edu/Ch19.WinBUGS/

simple.m

DeMere.odc, jeremy.odc, Regression1.odc, Regression2.odc,

simulationd.odc

alpha.txt, beta.txt, sigma.txt, tau.txt

CHAPTER REFERENCES

Congdon, P. (2001). Bayesian Statistical Modelling. Wiley, Hoboken.

Congdon, P. (2003). Applied Bayesian Models. Wiley, Hoboken.

Congdon, P. (2005). Bayesian Models for Categorical Data. Wiley, Hoboken.

Lunn, D. J., Thomas, A., Best, N., and Spiegelhalter, D. (2000). WinBUGS – a Bayesian

modelling framework: concepts, structure, and extensibility. Stat. Comput., 10, 325–

337.

Ntzoufras, I. (2009). Bayesian Modeling Using WinBUGS. Wiley, Hoboken.

Index

agreement, 112, 540

analysis of covariance (ANCOVA),

638

ANOVA

balanced design, 411

functional, 443

fundamental identity, 412

nested design, 436

one way, 410

repeated measures, 432

table, 412

testing contrasts, 417

two way, 424

arithmetic mean, 13

association measures, 537

contingency coefﬁcient C, 537

Cramer’s V, 537

φ coefﬁcient, 537

attribute, 6

AUC, 119

average prediction error, 626

Bayes’

factor, 88, 325

rule, 85–90, 113, 280

theorem, 283

Bayesian

computation, 293

estimation, 288

interval estimation, 298

networks, 90

prediction, 303

testing, 324

beta function, 167

bias, 238

bioequivalence, 320, 390

Schuirmann’s TOST, 390

Westlake’s conﬁdence interval, 391

blocking, 369, 430

Bonferroni

correction, 342

inequality, 67

Bonferroni–Holm method, 343

capture-recapture models, 147

CDF, 133, 157

censored observation, 702

central limit theorem (CLT), 204

Chebyshev’s inequality, 241

Chernoff faces, 41

circuit problem, 68

clog-log regression, 674

CLT, 204

coefﬁcient

of correlation, 30

coefﬁcient of variation (CV), 21

combinations, 76

concordance, 112

conﬁdence interval, 246

3/n rule, 258

Anscombe’s ArcSin, 255

Clopper-Pearson, 255

difference of normal means, 361

normal mean, 247

normal variance, 249

Poisson rate, 263

proportion, 253

quantiles, 262

Wald’s, 253

Wald’s corrected, 253

Wilson score, 254

Wilson’s, 254

conjugate priors, 287

consensus means, 305

contingency tables, 532

expected frequency, 534

contrasts, 416

Cook’s distance, 627

correlation, 30, 571

correlation coefﬁcient

B. Vidakovic, Statistics for Bioengineering Sciences: With MATLAB and WinBUGS Support, 747

Springer Texts in Statistics, DOI 10.1007/978-1-4614-0394-4,

748 Index

conﬁdence interval, 576

Kendall’s, 589

multiple, 585

partial, 573

Pearson’s, 572

Spearman’s, 586

testing

ρ =0, 574

testing

ρ =ρ

, 579

testing equality of two correla-

tions, 580

counting principles, 75

Cox proportional hazards model, 714

CR constraint, 422

credible set

equal-tail, 299

highest posterior density (HPD),

298

credible sets, 298

cumulative distribution function (CDF),

133, 157

cumulative hazard, 703

data, 2, 6

censored, 702

interval, 45

nominal, 45

ordinal, 45

ratio, 45

De Morgan’s laws, 66

delta method, 219

density

conditional, 159

joint, 159

marginal, 159

deviance, 665, 679

DFBETAS, 627

DFFITS, 627

distribution

Bernoulli, 141, 659

beta, 167

beta-binomial, 288

binomial, 141, 246

Cauchy, 214

chi-square, 209, 243

complementary log-log, 675

conditional, 138, 159

Dirichlet, 172

discrete uniform, 140, 483

empirical, 515

exponential, 162

F, 215

gamma, 165

Gaussian, 164, 193

geometric, 151

hypergeometric, 146, 713

inverse gamma, 166

Irwing-Hall, 162

Kolmogorov, 518

leptokurtic, 20

logistic, 169, 659

lognormal, 218

Lorentz, 214

marginal, 138, 159, 283

Maxwell, 236

multinomial, 155

negative binomial, 152

generalized, 154

noncentral

, 217, 540

noncentral F, 217, 439, 441, 634

noncentral t, 217, 335, 363

normal, 164, 193

bivariate, 197

Pareto, 171

platykurtic, 20

Poisson, 149

Polya, 154

posterior, 284

prior, 283

prior predictive, 284

probability, 132

Rayleigh, 175

sampling, 238, 243

Student’s t, 213

uniform, 161, 237

Weibull, 170

Wishart, 212, 585

diversity index

Shannon’s, 23

Simpson’s, 50

Index 749

effect size, 322

empirical cdf, 26

entropy, 158

equivalence tests, 389

error-in-variables regression, 637

errors in testing, 321

estimator

consistent, 239

Graybill-Deal, 305

interval, 246

Kaplan-Meier, 707

MLE, 232

moment matching, 231

product-limit, 707

robust, 244

Schiller-Eberhardt, 305

unbiased, 238

Wilson’s, 289

event, 63

complement, 64

impossible, 63

sure, 63

events

exclusive, 64

hypotheses, 83

independence, 79

intersection, 63

union, 64

failure rate, 163

false discovery rate (FDR), 343

familywise error rate (FWER), 342

FDA guidelines, 282

Fisher’s exact test, 546

ﬁve-number summary, 19

Friedman’s test, 492

pairwise comparisons, 494

functional ANOVA, 443

gamma function, 165

gauge R&R, 449

number of distinct categories (NDC),

451

percent of R&R variability (PRR),

451

repeatibility, 449

reproducibility, 449

geometric mean, 13

Gini’s mean difference, 244

grand mean, 411

Greenwood formula, 708

Hanszel–Mantel test, 712

harmonic mean, 13

hat matrix, 621

hazard function, 702

histogram, 24

Sturges rule, 24

homogeneity index

Shannon’s, 23

Simpson’s, 50

homogeneity measure, 23

hyperparameter, 283

i.i.d. random variables, 134

inclusion-exclusion rule, 64

incomplete beta function, 167

index

Quetelet, 192

Youden, 120

inter-quartile range (IQR), 18

interaction plots, 428

Jarque–Bera test, 521

Kaplan–Meier estimator, 706, 710

Kolmogorov’s test, 517

Kolmogorov-Smirnov test, 515

Kruskal–Wallis test, 490, 491

pairwise comparisons, 492

kurtosis, 20

leptokurtic, 20

platykurtic, 20

Laud–Ibrahim predictive criterion,

633

law of large numbers (LLN), 241

leptokurtic, 20

likelihood, 283

ratio

negative, 112

positive, 112

750 Index

ratio negative, 113

ratio positive, 113

Likert scale, 45

Lilliefors’ test, 517, 522

log-linear models, 684

logistic regression, 658

Cox-Snell R

, 667

deviance, 665

deviance residuals, 666

Effron’s pseudo-R

, 667

half-normal plots, 666

Hosmer–Lemeshow statistic, 666

McFadden’s pseudo-R

, 667

Nagelkerke’s pseudo-R

, 667

Pearson’s

, 666

Wald’s test, 664

logrank test, 712

MAD, 17

Mahalanobis transformation, 36

Mantel–Haenszel test, 548

Marascuillo procedure, 454

margin of error, 259

Markov chain, 178

Markov chain Monte Carlo (MCMC),

294

MATBUGS, 740

maximum likelihood estimation (MLE),

232

McNemar’s test, 552

mean

arithmetic, 13

geometric, 13

harmonic, 13

posterior, 289

prior, 289

sample, 13

trimmed, 15

winsorized, 15

mean residual life (mrl), 703

mean square error (MSE), 238

median, 14, 15

life, 703

memoryless property, 152, 163, 184

Miettinen’s test, 555

mixtures, 177

mode, 14

moment generating function, 135

Moran’s test, 521

multicollinearity, 620

multiplication rule, 75

multivariable regression, 619

ANOVA table, 622

Cook’s distance, 627

DFBETAS, 626

DFFITS, 627

forward/backward variable selec-

tion, 631

inference for parameters, 624

inﬂuence analysis, 627

Mallows’ C

, 632

polynomial, 635

PRESS residuals, 626

residual analysis, 625

sample size, 634

variable selection, 631

n-choose-k

, 74

negative

false, 111

true, 111

Nelson–Aalen estimator, 709

nested design, 436

normal equations, 621

null hypothesis (H

), 319

odds, 71

odds ratio, 383

paired tables, 555

OpenBUGS, 734

order statistic, 14

orthogonal contrasts, 418

paired t-test, 367

paired tables, 552

Miettinen’s test, 555

RGB estimator, 555

pairwise comparisons, 419

Friedman’s test, 494

Kruskal–Wallis test, 492

variable inﬂation factor (VIF), 630

Index 751

Scheffee’s procedure, 421

Sidak’s procedure, 421

Tukey’s procedure, 419

parameter, 6

PDF, 133, 157

Pearson’s

-test, 508

permutations, 76

pie charts, 27

platykurtic, 20

plot

Andrews, 39

parallel coordinates, 39

star, 41

PMF, 133

Poisson process, 511

Poisson regression, 678

Anscombe residuals, 679

deviance, 679

deviance residuals, 679

Friedman-Tukey residuals, 679

Poissonness plots, 506

population, 2, 6

positive

false, 111

true, 111

posterior distribution, 284

power

retrospective, 375

two normal variances, 374

two sample t-test, 362

power of the test, 322

prediction intervals, 260

predictive value

negative, 112

positive, 112

prevalence, 112

prior, 283

conjugate, 287

elicitation, 290, 291

enthusiastic, 293

Jeffreys’, 292

noninformative, 292

sample size, 289

skeptic, 293

vague, 293

probability

conditional, 78

distribution function (PDF), 133,

157

mass function (PMF), 133

total, 84

probit regression, 674

product-limit estimator, 707

p-value, 323

Q–Q plots, 27, 211, 504, 505

R&R study, 449

random variable, 131

continuous, 157

moments, 158

discrete, 133

expectation, 133

variance, 134

quantiles, 156

transformation, 174

random variables

correlation, 140

covariance, 139

i.i.d., 134

independent, 134, 138, 159

jointly distributed, 159

range, 18

ranks, 481, 482

receiver operating characteristic

regression, 600

ANOVA table, 604

error-in-variables, 637

multivariable, 619

testing a new response, 612

testing equality of slopes, 616

testing intercept

, 609

testing mean response, 611

testing slope

, 608

testing variance

, 610

relative risk, 382

paired tables, 554

repeatability, 449

repeated measures design, 431

sphericity tests, 435

curve, 118

752 Index

reproducibility, 449

residuals

Anscombe, 671, 679

deviance, 666, 671, 679

externally studentized, 626

Friedman-Tukey, 679

Pearson, 666

PRESS, 626

studentized, 626

risk difference

paired tables, 554

risk differences, 381

risk ratio, 382

paired tables, 554

ROC curve, 118

rule

Bayes, 86

total probability, 84

sample, 2, 6

central moments, 20

composite, 22

correlation, 31

covariance, 30

covariance matrix, 34

mean, 13

moments, 19

multivariate, 33

percentile, 18

quantile, 18

simple, 22

standard deviation, 16

variance, 16

sample size

ANOVA, 438, 441

by conﬁdence interval, 259

contingency tables, 539

paired t-test, 373

regression, 634

repeated measures design, 442

two normal means, 362

two normal variances, 374

two proportions, 379

sample standard deviation

pooled, 357

sample variance

pooled, 357

scatterplot, 39

sensitivity, 112

sensitivity/speciﬁcity of combined

tests, 116

sigma rules, 197

sign test, 478

signiﬁcance level, 321

Simpson’s paradox, 698

skewness, 20

Smirnov’s test, 517

speciﬁcity, 112

standard error (s.e.), 239

statistic

t, 332, 357

z, 330

Pearson’s

, 534

statistical hypothesis, 318

statistical model, 6

Stuart–Maxwell test, 559

STZ constraint, 411, 422, 685

survival function, 702

tables

association, 537

contingency, 534

Fisher’s exact test, 546

paired, 552

three way (r

×c × p), 543

two way (r

×c), 533

test

Fisher’s exact, 546

Jarque-Bera, 521

Kolmogorov’s, 516

Kolmogorov-Smirnov, 515

Lilliefors’, 522

logrank, 712

Mantel–Haenszel, 548

McNemar’s, 552

Pearson’s

, 508

Smirnov’s, 517

Stuart-Maxwell, 559

testing hypotheses

equivalence tests, 389