Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

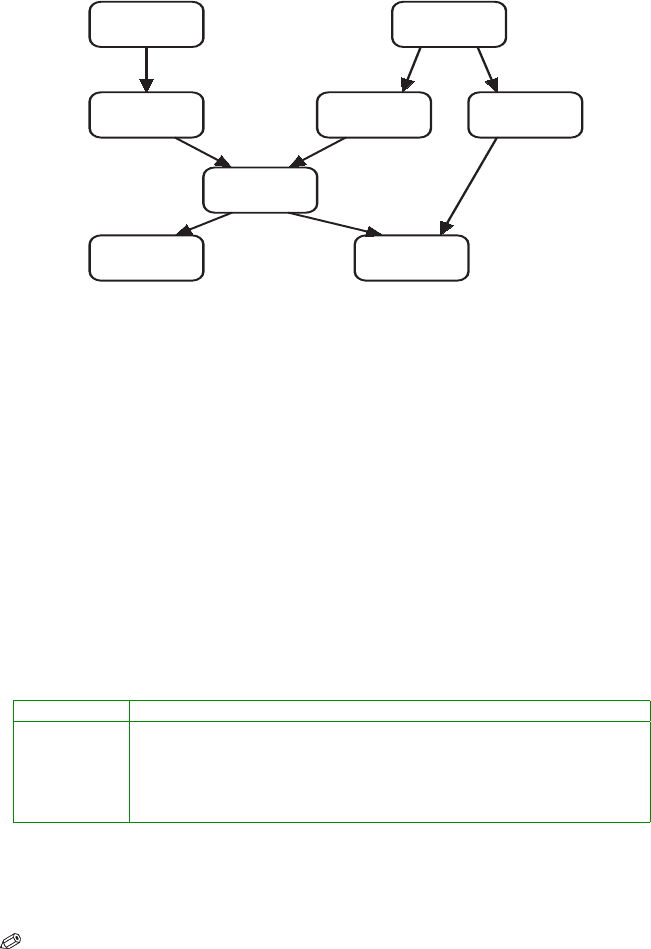
3.9 Bayesian Networks* 95

Visit to Asia?

Has

Tuberculosis

Smoker?

Has

Bronchitis

Dyspnoea ?

Has Lung

Cancer

Tuberculosis

or Cancer

Positive

X-ray?

Fig. 3.17 Lauritzen and Spiegelhalter’s (1988) Asia Bayes net: a ﬁctitious expert system

representing the diagnosis of a patient having just returned from a trip to Asia and showing

dyspnoea.

p.lung.cancer = structure(.Data = c(0.99,0.01,0.90,0.10),

.Dim = c(2,2)),

p.xray = structure(.Data = c(0.95,0.05,0.02,0.98),

.Dim = c(2,2)),

p.dyspnoea = structure(.Data = c(0.9,0.1,

0.2,0.8,

0.3,0.7,

0.1,0.9), .Dim = c(2,2,2)))

INITS

list(smoking = 1, tuberculosis = 1,

lung.cancer = 1, bronchitis = 1, xray = 1)

mean sd MC error val2.5pc median val97.5pc start sample

bronchitis 1.812 0.3904 0.003988 1.0 2.0 2.0 2001 10000

lung.cancer 1.099 0.2985 0.003345 1.0 1.0 2.0 2001 10000

smoking 1.618 0.4859 0.004976 1.0 2.0 2.0 2001 10000

tuberculosis 1.095 0.2928 0.002706 1.0 1.0 2.0 2001 10000

xray 1.224 0.4171 0.004132 1.0 1.0 2.0 2001 10000

The results should be interpreted as follows. If the patient who visited Asia

experiences dyspnoea (hard evidence in

DATA: asia=2, dyspnoea = 2), then the

probabilities of bronchitis, lung cancer, being a smoker, tuberculosis, and a

positive xray, are 0.812, 0.099, 0.618, 0.095, and 0.224, respectively.

96 3 Probability, Conditional Probability, and Bayes’ Rule

3.10 Exercises

3.1. Event Differences. Recall that the difference between events A and B

was deﬁned as A

\B = A ∩B

. Using Venn diagrams demonstrate that

(a) A

\(A\B) = A ∩B and A\(B\A) = A,

(b) A

\(B\C) =(A ∩C) ∪ (A ∩B

3.2.

(a) Using MATLAB to count favorable outcomes, ﬁnd the probability that

the selected number is divisible by at least one of 3, 5, or 7.

(b) Compare this probability with a naïve solution 1/3 + 1/5 + 1/7 - 1/15 -1/21

- 1/35 + 1/105 = 0.542857, and show that the naïve solution is correct!

{1,2,.. . , N} if N =316?

(d) Is the naïve solution correct for any other N from

{289,290,.. . 340}? Plot

this probability for 289

≤ N ≤340. Is there any symmetry in the plot?

3.3. A Complex Circuit. Figure 3.18 shows a circuit S that consists of iden-

tical components e

, i =1,...,13 that work (and fail) independently of each

other. Any component is operational in some ﬁxed time interval with prob-

ability 0.8.

Fig. 3.18 Each of 13 independent components in the circuit is operational with probability

0.8.

(a) Calculate the probability that circuit S is operational.

(b) Write a MATLAB program that approximates the probability in (a) by

simulation.

Inclusion-Exclusion Principle in MATLAB.

From the set

{1,2, 3,...,315

}

a number is selected at random.

3.10 Exercises 97

3.4. De Mere Paradoxes. In 1654 the Chevalier de Mere asked Blaise Pascal

(1623–1662) the following two questions:

(a) Why would it be advantageous in a game of dice to bet on the occurrence

of a 6 in 4 trials but not advantageous in a game involving two dice to bet

on the occurrence of a double 6 in 24 trials?

(b) In playing a game with three dice, why is a sum of 11 more advantageous

than a sum of 12 when both sums are the result of six conﬁgurations:

11: (1, 4, 6), (1, 5, 5), (2, 3, 6), (2, 4, 5), (3, 3, 5), (3, 4, 4);

12: (1, 5, 6), (2, 4, 6), (2, 5, 5), (3, 3, 6), (3, 4, 5), (4, 4, 4)?

How would you respond to the Chevalier?

3.5. Probabilities of Some Composite Events. Show that for arbitrary

events A, B,

(a)

P(A∆B) =P(A ∪B) −P(AB) =P(A) +P(B)−2P(AB);

(b)

P(A∆B) ≥|P(A) −P(B)|.

P(AC∆BC) ≤P(A∆B) and

(d) (

P(A) +P(B))

1+2P(AB)/(P(A)+P(B))

≤P(A ∪B) ≤P(A) +P(B).

3.6. Deighton’s Novel. In his World War II historical novel Bomber Len

Dieghton argues that a pilot is “mathematically certain” to be shot down

in 50 missions if the probability of being shot down on each mission is 0.02.

(a) Assuming independence of outcomes in each mission, is Deighton’s rea-

soning correct?

(b) Find the probability of surviving all 50 missions without being shot

down?

3.7. Reliable System from Unreliable Components. NASA is asking you

to design a system that reliably performs a task on a space shuttle in the

next 3 years with probability of 0.999999

= 1 −10

−6

. In other words, the

probability of failing during the next three years should not exceed one in a

million. However, at your disposal you have components that in the next 3

years will fail with a probability of 0.2. Luckily, the weight and price of the

components are not an issue and you can combine/link them to increase the

system’s reliability.

(a) Should you link the components in a serial or parallel fashion to increase

the probability of reliable performance?

(b) What minimal number of components should be linked as in (a) to satisfy

NASA’s requirement of 0.999999 probability of reliable performance?

3.8. k-out-of-n Systems. Suppose that n independent components constitute

an engineering system. The system is called a k-out-of-n system if it works

only when k or more components are operational. This particular system

has four components that are operational with probabilities 0.1,0.8,0.5, and

0.4. If the system is a 2-out-of-4, what is the probability that it works?

98 3 Probability, Conditional Probability, and Bayes’ Rule

3.9. Number of Dominos. How many different dominos are a sample space if

the number of dots on the dominos ranges between (a) 0 and 3, (b) 0 and 8,

and (c) 0 and 16, inclusive?

3.10. Counting Protocols. Adel et al. (1993) applied various orders in drug

combination sequence studies in search of a cure for human endometrial

carcinoma. Four drugs A–D were evaluated for sequence-dependent inhibi-

tion of human tumor colony formation in soft agar.

(a) How many protocols are needed to evaluate all possible sequences of the

four drugs?

(b) How many protocols are possible when only two drugs out of four are to

be administered if the order of their administration is (i) important or (ii)

not important?

sequent to each other because of cumulative toxicity concerns, how many

protocols are possible if the order of drug administration is to be evaluated?

3.11. Correlation Between Events. The correlation between events A and B

is deﬁned as

Corr(A,B) =

(A ∩B) −P(A)P(B)

P(A)(1 −P(A))

P(B)(1−P(B))

Show that

Corr(A, A) =1 and Corr(A,B) =Corr(A

3.12. A Fair Gamble with a Possibly Loaded Coin. Suppose you have a coin

for which you do not know the probability of its landing heads up. You sus-

pect that the coin is loaded and that the probability of heads differs from

1/2.

(a) Can you emulate a fair coin by ﬂipping the possibly biased one?

(b) Can you emulate the rolling of a fair die by ﬂipping the possibly biased

coin?

Hint:

You may need to ﬂip the coin more than once.

3.13. Neural Signal. A neuron will ﬁre at random at any moment in [0,T], with

a probability of p. If up to time t

< T the neuron does not ﬁre, what is the

probability that it will ﬁre in the remaining time, (t, T]?

3.14. Guessing. Subjects in an experiment are told that either a red or a green

light will ﬂash. Each subject is to guess which light will ﬂash. The subject

is told that the probability of a red light is 0.7, independently of guesses.

Assume that the subject is a probability matcher, that is, guesses red with

a probability of 0.7 and green with a probability of 0.3.

(a) What is the probability that the subject will guess correctly?

(b) Given that a subject guesses correctly, what is the probability that the

light ﬂashed red?

3.10 Exercises 99

3.15. Propagation of Genes. The following example shows how the ideas of

independence and conditional probability can be employed in studying ge-

netic evolution. Consider a single gene that has two forms, recessive (R) and

dominant (D). Each individual in the population has two genes in his/her

chromosomes and thus can be classiﬁed into the genotypes DD, RD, and

RR. If an individual is drawn at random from the nth generation, then

the probabilities of the three genotypes will be denoted by p

,2r

, and q

respectively. (Clearly, p

+2 r

=1.)

The problem is expressing the probabilities p

, q

, and r

in terms of ini-

tial probabilities p

, q

, and r

and the method of reproduction. In random

Mendelian mating, a single gene from each parent is selected at random

and the selected pair determines the genotype of the offspring. These selec-

tions are carried independently of each other from generation to generation.

Let M

be the event that R is chosen from the male and F

be the event

that R is chosen from the counterpart female. Events M

and F

are inde-

pendent and have the same probability. Thus:

P(M

) = P (RR) ×P(M

|RR) +P(RD) ×P(M

|RD) +P(DD) ×P(M

|DD)

= P(RR) ×1 +P(RD) ×1/2 +P(DD) ×0

= q

+2r

= q

by the rule of total probability.

By the independence of M

and F

n+1

=P(M

∩F

) =P(M

) ·P(F

) =(q

)

Similarly,

n+1

=(p

)

and

n+1

=1 − p

n+1

−q

n+1

The above equations govern the propagation of genotypes in this popula-

tion.

Start with any initial probabilities p

, q

, and r

. (Say, 0.3, 0.3, and 0.2; re-

member to check: 0.3

+0.3+2·0.2 =1.) Find iteratively (p

, q

, r

),(p

, q

, r

and (p

, q

, r

), and demonstrate that p

= p

, q

= q

, and

= r

. The fact that the probabilities remain the same is known as the

Hardy–Weinberg law. It does not hold if other factors (mutation, selection,

dependence) are introduced into the model.

3.16. Easy Conditioning. Assume

P(rain today) = 40%, P(rain tomorrow) =

50%, and P(rain today and tomorrow) =30%. Given that it is raining today,

what is the chance that it will rain tomorrow?

100 3 Probability, Conditional Probability, and Bayes’ Rule

3.17. Eye Color. The eye color of a child is determined by a pair of genes, one

from each parent. If {b} and {B} denote blue- and brown-eyed genes, then a

child can inherit the following pairs: {bb}, {bB}, {Bb}, and {BB}. The {B} gene

is dominant, that is, the child will have brown eyes when the pairs are {Bb},

{bB}, or {BB} and blue eyes only for the {bb} combination. A parent passes

to a child either gene from his/her pair with equal probability.

Megan’s parents are both brown-eyed, but Megan has blue eyes. Megan’s

brown-eyed sister is pregnant and her husband has blue eyes. What is the

probability that the baby will have blue eyes?

3.18. Dice. In rolling ten fair dice we have information that at least one

ap-

peared. What is the probability that there were at least two

3.19. Inﬂation and Unemployment. Businesses commonly project revenues

under alternative economic scenarios. For a stylized example, inﬂation

could be high or low and unemployment could be high or low. There are

four possible scenarios, with the following assumed probabilities:

Scenario

Inﬂation Unemployment Probability

1 High High 0.16

High Low 0.24

Low High 0.36

Low Low 0.24

(a) What is the probability of high inﬂation?

(b) What is the probability of high inﬂation if unemployment is high?

3.20. Multiple Choice. A student answers a multiple choice examination ques-

tion that has four possible answers. Suppose that the probability that the

student knows the answer to a question is 0.80 and the probability that the

student guesses is 0.20. If the student guesses, the probability of guessing

the correct answer is 0.25.

(a) What is the probability that the ﬁxed question will be answered cor-

rectly?

(b) If it is answered correctly, what is the probability that the student really

knew the correct answer?

3.21. Manufacturing Bayes. A factory has three types of machines producing

an item. The probabilities that the item is conforming if it is produced on

the ith machine are given in the following table:

This description is simpliﬁed, and in fact there are several genes affecting eye color and

the amount of yellow and black pigments in the iris, leading to shades of colors including

green and hazel.

3.10 Exercises 101

Type of machine Probability of item conforming

1 0.94

2 0.95

3 0.97

The total production is distributed among the machines as follows: 30% is

done on type 1, 50% on type 2, and 20% on type 3 machines. One item is

selected at random from the production.

(a) What is the probability that it is conforming?

(b) If it is conforming, what is the probability that it was produced on a

type 1 machine?

3.22. Stanley. Stanley takes an oral exam in statistics with several other stu-

dents. He needs to answer the questions from an examination card drawn

at random from the set of 20 cards. There are exactly 8 favorable cards

among the 20 to which Stanley knows the answers. Stanley will get a grade

of A if he knows the answers, that is, if he draws a favorable card. What is

the probability that Stanley will get an A if he draws the card standing in

line (a) ﬁrst, (b) second, and (c) third?

3.23. Kokomo, Indiana. In Kokomo, IN, 65% of the people are conservative,

20% are liberal, and 15% are independent. Records show that in a particu-

lar election, 82% of conservatives voted, 65% of liberals voted, and 50% of

independents voted. If a person from the city is selected at random and it

is learned that she did not vote, what is the probability that the person is

liberal?

3.24. Mysterious Transfer. Of two bags, one contains four white balls and

three black balls and the other contains three white balls and ﬁve black

balls. One ball is randomly selected from the ﬁrst bag and placed unseen in

the second bag.

(a) What is the probability that a ball now drawn from the second bag will

be black?

(b) If the second ball is black, what is the probability that a black ball was

transferred?

3.25. Two Masked Robbers. Two masked robbers try to rob a crowded bank

during the lunch hour, but the teller presses a button that sets off an alarm

and locks the front door. The robbers, realizing they are trapped, throw

away their masks and disappear into the chaotic crowd. Confronted with

40 people claiming they are innocent, the police give everyone a lie detector

test. Suppose that guilty people are detected with a probability of 0.85 and

innocent people appear to be guilty with a probability of 0.08. What is the

probability that Mr. Smith was one of the robbers given that the lie detector

says he is a robber?

3.26. Information Channel. One of the three words AAAA, BBBB, and CCCC

is transmitted via an information channel. The probabilities of these words

102 3 Probability, Conditional Probability, and Bayes’ Rule

being transmitted are 0.3, 0.5, and 0.2, respectively. Each letter is transmit-

ted and received correctly with a probability of 0.6, independently of other

letters. Since the channel is not perfect, the transmitted letter can change

to one of the other two letters with an equal probability of 0.2. What is

the probability that the word AAAA was submitted if the word ABCA is

received?

3.27. Quality Control. An automatic machine in a small factory produces metal

parts. Most of the time (90% according to long-term records), it produces

95% good parts, while the remaining parts have to be scrapped. Other

times, the machine slips into a less productive mode and only produces 70%

good parts. The foreman observes the quality of parts that are produced by

the machine and wants to stop and adjust the machine when she believes

that the machine is not working well. Suppose that the ﬁrst dozen parts

produced are given by the sequence

s u s s s s s s s u s u

where s is satisfactory and u is unsatisfactory. After observing this se-

quence, what is the probability that the machine is in its productive state?

If the foreman wishes to stop the machine when the probability of “good

state” is under 0.7, when should she stop it?

3.28. Let’s Make a Deal. Monty Hall was the host of the once-popular tele-

vision game show Let’s Make a Deal. At certain times during the show,

a contestant was allowed to choose one of three identical doors A, B, and

C, behind only one of which was a valuable prize (a new car). After the

contestant picked a door (say, door A), Monty opened another door and

showed the contestant that there was no prize behind that door. (Monty

knew where the prize was and always chose a door where there was no

prize.) He then asked the contestant whether he wanted to stick with his

choice of door or switch to the remaining unopened door. Should the contes-

tant have switched doors? Did it matter?

3.29. Ternary Channel. A communication system transmits three signals,

, s

, or s

, with equal probabilities. The reception is corrupted by noise,

causing the transmission to be changed according to the following table of

conditional probabilities:

Received

0.75 0.1 0.15

Sent s

0.098 0.9 0.002

0.02 0.08 0.9

The entries in this table list the probability that s

is received, given that s

is sent, for i, j =1,2,3. For example, if s

is sent, the conditional probability

of receiving s

is 0.15.

3.10 Exercises 103

(a) Compute the probabilities that s

, s

, and s

are received.

(b) Compute the probabilities

P(s

sent |s

received ) for i, j = 1, 2,3. (Com-

plete the table.)

Sent

0.8641

Received s

0.0741

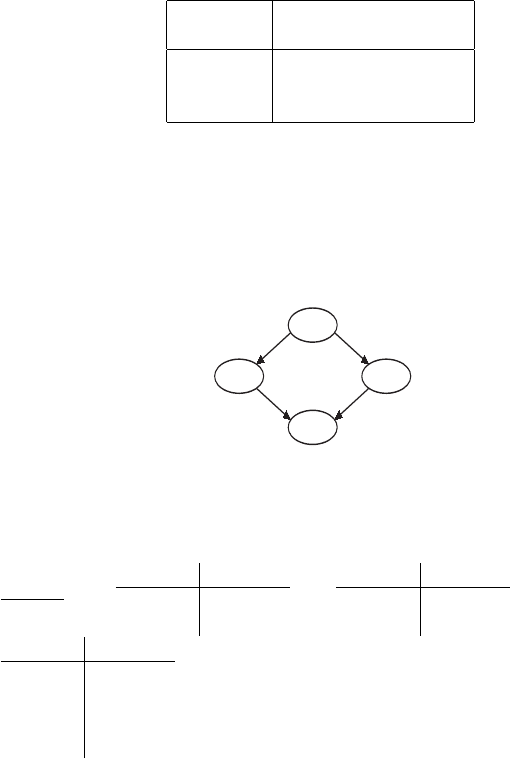
3.30. Sprinkler Bayes Net. Suppose that a sprinkler (S) or rain (R) can make

the grass in your yard wet (W). The probability that the sprinkler was on

depends on whether the day was cloudy (C). The probability of rain also

depends on whether the day was cloudy. The DAG for events C, S, R, and W

is shown in Fig. 3.19.

C

S R

W

Fig. 3.19 Sprinkler Bayes net.

The conditional probabilities of the nodes are given in the following tables.

0.5 0.5

S Condition

0.50 0.50 C

0.90 0.10 C

R Condition

0.80 0.20 C

0.20 0.80 C

W Condition

1 0 S

0.10 0.90 S

0.10 0.90

S R

0.01 0.99 S R

Using WinBUGS, approximate the probabilities

(a)

P(C|W), (b) P(S|W

), and (c) P(C|R,W

3.31. Diabetes in Pima Indians. The Pima Indians have the world’s highest

reported incidence of diabetes. Since 1965, this population has participated

in a longitudinal epidemiological study of diabetes and its complications.

The examinations have included a medical history for diabetes and other

major health problems. A population of women who were at least 21 years

old, of Pima Indian heritage, and living near Phoenix, AZ was tested for

diabetes according to World Health Organization criteria.

104 3 Probability, Conditional Probability, and Bayes’ Rule

The following conditions (“events”), constructed from the database, can be

related to a randomly selected subject from this population.

Event Description

P Three or more pregnancies

A Older than the database median

age

O Heavier than the database me-

dian weight

D Diagnosis of diabetes

G High plasma glucose concentra-

tion in an oral glucose tolerance

test

I High 2-h serum insulin (µU/ml)

B High blood pressure

The DAG in Fig. 3.20 simpliﬁes the proposal of Tom Bylander from the

University of Texas in San Antonio, who used Bayesian networks and the

Pima Indians Diabetes Database in a machine learning example.

P A O

G I B

Fig. 3.20 Pima Indians diabetes Bayes net.

From 768 complete records relative frequencies are used to approximate

the conditional probabilities of the nodes. The probabilities are given in the

following tables.

0.45 0.55

0.5 0.5

D condition

0.95 0.05 P

0.67 0.33 P

0.59 0.41

A O

0.40 0.60 P

A O

D condition

0.73 0.27 P A

0.66 0.34 P A

0.63 0.37

P A O

0.41 0.59 P A O

http://www.cs.utsa.edu/~bylander/cs6243/bayes-example.pdf