Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support
Подождите немного. Документ загружается.


3.5 Counting Principles* 75
Ã
n
k
!
=
Ã
n
n
−k
!
,
Ã
n
0
!
=
1 and
Ã
n
1
!
=
n,
Ã
n
k
!
+
Ã
n
k
+1
!
=
Ã
n +1
k
+1
!
.
Fundamental Counting Principle . If an experiment consists of k
actions, and the ith action can be performed in n
i
different ways, then
the whole experiment can be performed in n
1
×n
2
×···×n
k
different ways.
This is called the multiplication counting rule or fundamental counting
principle.
Example 3.7. Out of 15 items, 4 are defective. The items are inspected one by
one. What is the probability that the ninth item was the last defective one?
Consider the arrangement of 11 conforming and 4 defective items. The
number of all possible arrangements is
¡
15
4
¢
=
¡
15
11
¢
=
1316, as one chooses 4
places out of 15 to place defective items or, equivalently, 11 places out of 15 to
place conforming items.
The number of favorable outcomes can be found by the multiplication rule.
Favorable outcomes are defined as follows: among the first-selected eight items
three are defective, the ninth position is occupied by a defective item, and none
of the remaining six items is defective:
Ã
8
3
!
×
1 ×1 =56.
Note that the number of ways in which a defective item falls at the ninth
position, and the number of ways where six fair items occupy positions 10 to
15, are 1 each. Thus, the required probability is 56/1365
=0.041.
There is also an addition counting rule that mimics the additive property
of probability: If k events are exclusive and have n
1
,n
2
,... , n
k
outcomes, then
their union has n
1
+n
2
+···+n
k
outcomes. If the events are not exclusive, this
rule is known as the inclusion-exclusion principle. For instance, if two events
are arbitrary, the inclusion-exclusion rule count for outcomes in their union is
n
1
+n
2
−n
12
, where n
12
is the number of common outcomes. For three events
the inclusion-exclusion rule is n
1
+n
2
+n
3
−n
12
−n
13
−n
23
+n
123
; cf. (3.2).
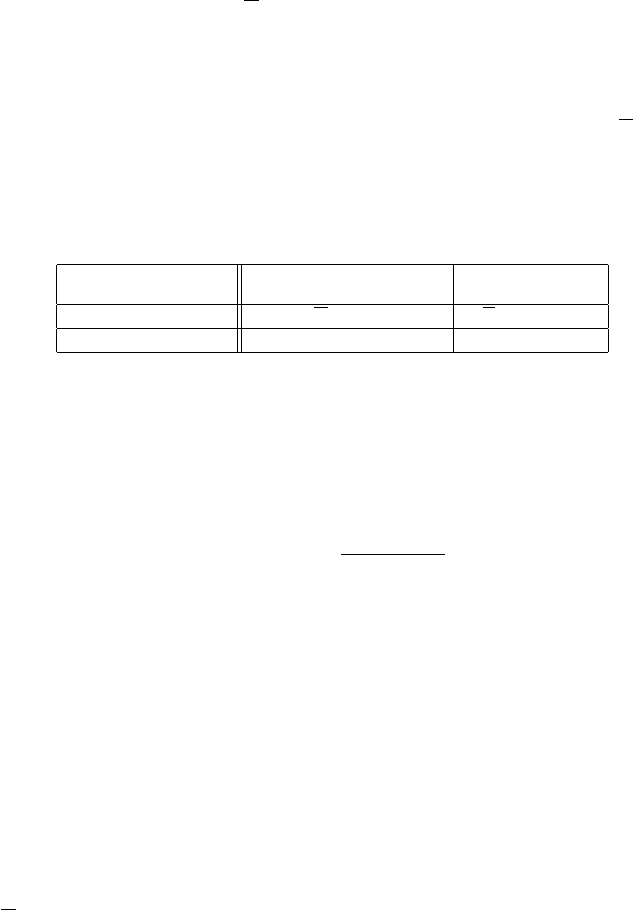
If the population has N subjects and a sample of size n is needed, then
Table 3.1 summarizes the number of possible samples, given the sampling
policy and importance of ordering.
76 3 Probability, Conditional Probability, and Bayes’ Rule
We first introduce the necessary notation. When the order is important, the
samples are called variations or permutations. One can think about variations
as words in an alphabet, since for words the order of letters is important. By
the fundamental counting principle, the number of variations with repetitions
of N elements of length n is
V
n
N
= N
n
since each of n places can be selected in
N ways. The number of variations without repetition of N elements of length
n is V
n
N
= N ×(N −1) ×···×(N −n +1) = N
(n)
, n ≤ N. Note that V
N
N
= N! is the
number of permutations of N distinct elements.
In combinations, the order in the sample is not important. If there is no
repetition of elements, then C
n
N
=
¡
N
n
¢
. If the repetition is possible, then C
n
N
=
¡
N+n−1
n
¢
.
Table 3.1 Number of variations/combinations when the selection of n from N elements is
done with/without the repetition.
Order important Order not important
(variations or permutations) (combinations)
Sampling w/ repetition V
n
N
= N
n
C
n
N
=
¡
N+n−1
n
¢
Sampling w/o repetition V
n
N
= N(N −1). .. (N −n +1) C
n
N
=
¡
N
n
¢
, n ≤ N
The number of permutations of N distinctive elements is N!, but if among
N elements there are only k different elements, n
1
of type 1, n
2
of type 2, . . . ,
n
k
of type k, (n
1
+n
2
+···+n
k
= N), then the number of different permutations
is
Ã
N
n
1
, n
2
,... n
k
!
=
N!
n
1
!n
2
!···n
k
!
. (3.4)
The number in (3.4) is also called the multinomial coefficient.
Example 3.8. Probability by Counting. What is the probability that in a
six-digit licence plate of a randomly selected car
(a) All digits will be different?
(b) Exactly two digits will be equal?
(c) At least three digits will be different?
(d) There will be exactly two pairs of equal digits?
We assume that any digit from 0 to 9 can be at any of the six positions in
the six-digit plate number.
This example is solved by using the classical definition of probability. For
each event in (a)–(d), the number of favorable outcomes will be divided by the
number of possible outcomes. The number of all possible outcomes is common,
V
6
10
=10
6
.
(a) To find the number of favorable outcomes for the event where all digits
are different, consider forming a six-digit number position by position. For the

3.5 Counting Principles* 77
first position there are ten digits available, for the second nine (the digit used
in the first position is eliminated as a choice for the second position), for the
third eight, etc., for the last five. By the fundamental counting principle, the
number of all favorable outcomes is the product 10
×9×8×7×6×5 =10
(6)
=V
6
10
,
and the probability is
10
(6)
10
6
=0.1512.
(b) Out of ten digits choose one and place it on any two positions out of six
available. This can be done in 10
×
¡
6
2
¢
=
150 ways. The remaining four positions
could be chosen in 9
×8 ×7 ×6 ways. Thus, the number of favorable outcomes
is 150
×9 ×8 ×7 ×6, and the required probability is 0.4536.
(c) The opposite event for “at least three digits are different” is “all digits
are the same” or “exactly two digits are the same,” and we will find its proba-
bility first. The number of cases where all digits are the same is ten, while the
number of cases where there are exactly two different digits is
¡
10
2
¢
×
(2
6
−2).
Digits a and b can be selected in
¡
10
2
¢
ways. Given the fixed selection, there
are 2
6
−2 words in alphabet {a, b} of length 6 where the words aaaaaa and
bbbbbb are excluded. The probability of “at least three different digits” is
1
−
10 +
¡
10
2
¢
(2
6
−2)
10
6
=1 −0.0028 =0.9972.
(d) From ten digits first select two for the two pairs, and then an additional
two digits for the remaining two places. There are four different digits: a, b for
the two pairs and c, d for the remaining two places. The selection can be done
in
¡
10
2
¢
×
¡
8
2
¢
ways. Once selected, the digits can be arranged in
¡
6
2,2,1,1
¢
=
6!
2!2!1!1!
ways, by using permutations with repetitions as in (3.4).
Thus, the probability is
¡
10
2
¢
×
¡
8
2
¢
×
6!
2! 2! 1! 1!
10
6
=0.2268.
The following two important equations for probability calculation are a
direct consequence of the combinatorial properties discussed in this section.
They will be used later in the text when discussing the binomial and hyperge-
ometric distributions and their generalizations.
Multinomial and Multihypergeometric Trials. Suppose that an ex-
periment can result in m possible outcomes, A
1
, A
2
,... , A
m
, that have
probabilities
P(A
1
) = p
1
,... , P(A
m
) = p
m
, p
1
+···+ p
m
=1. If the experi-
ment is independently repeated n times, then the probability that event

78 3 Probability, Conditional Probability, and Bayes’ Rule
A
1
will appear exactly n
1
times, A
2
exactly n
2
times, . . . , A
m
exactly n
m
times (n
1
+···+n
m
= n) is
Ã
n
n
1
, n
2
,... n
m
!
p
n
1
1
p
n
2
2
···p
n
m
m
.
If a finite population of size m has k
1
subjects of type 1, . . . , k
p
sub-
jects of type p, (k
1
+···+k
p
= m), and n subjects are sampled at random,
then the probability that x
1
will be of type 1, . . . , x
p
will be of type p
(x
1
+···+x
p
= n), is
¡
k
1
x
1
¢¡
k
2
x
2
¢
···
¡
k
l
x
l
¢
¡
m
n
¢
.
3.6 Conditional Probability and Independence
Important contemporary applications of probability in bioengineering, medical
diagnostics, system biology, bioinformatics, etc. concern modeling and predic-
tion of causal relationships in complex systems. The methodologies include in-
fluence diagrams, Bayesian networks, Granger causality, and related methods
for which the notions of conditional probability, causality, and independence
are fundamental. In this section we discuss conditional probabilities and in-
dependence.
A conditional probability is the probability of one event if we have informa-
tion that another event, typically from the same sample space, has occurred.
In the die-toss example, the probability of event A
={ } is P(A) =
1
6
. But what
if we knew that event B
={ , , , } occurred? There are only four possible
outcomes, only one of which is favorable for A. Thus, the probability of A given
B is
1
4
. The conditional probability of A given B is denoted as P(A|B).
In general, the conditional probability of an event A given that B has oc-
curred is equal to the probability of their intersection
P(AB) divided by the
probability of the event that we are conditioning upon,
P(B). Of course, event B
has to have a positive probability,
P(B) >0, because conditioning upon an event
of zero probability is equivalent to the indeterminacy 0/0, as 0
≤P(AB) ≤P(B):
P(A|B) =
P
(A ·B)
P(B)
, for
P(B) >0.

3.6 Conditional Probability and Independence 79
Figure 3.11 gives a graphical description of the conditional probability
P(A|B). Once event A is conditioned by B, B “becomes the sample space” and
B’s Venn diagram expands by a factor of
1
P(B)
. The intersection AB in the ex-
panded B becomes event A
|B.
Fig. 3.11 Graphical illustration of conditional probability.
An event A is independent of B if the conditional probability of A given B
is the same as the probability of A alone.
Events A and B are independent if
P(A|B) =P(A). (3.5)
In the die-toss example,
P(A) =
1
6
and P(A|B) =
1
4
. Therefore, events A
and B are not independent.
We saw that the probability of the union A
∪B was P(A ∪B) = P(A)+P(B)−
P
(AB). Now we are ready to introduce the general rule for the probability of
an intersection.
The probability that events A and B will both occur is obtained by ap-
plying the multiplication rule:
P(A ·B) =P(A)P(B|A) =P(B)P(A|B), (3.6)
where
P(A|B) and P(B|A) are conditional probabilities of A given B and
of B given A, respectively.
Only for independent events, equation (3.6) simplifies to
P(A ·B) =P(A)P(B). (3.7)
80 3 Probability, Conditional Probability, and Bayes’ Rule
Relationship (3.7) is also used to define independence, but (3.5) and (3.7) are
equivalent.
With the repeated application of the multiplication rule, one can easily
show
P(A
1
A
2
... A
n
) =P(A
1
|A
2
... A
n
) P(A
2
|A
3
... A
n
) ...P(A
n−1
|A
n
) P(A
n
),
which is sometimes referred to as the chain rule. Here is one example of the
use of the chain rule.
Example 3.9. 3+3 Dose Escalation Scheme. In a dose finding stage of clini-
cal trials (Phase I) patients are given the drug at some dose, and if there is no
dose limiting toxicity (DLT), the dose is escalated. A version of the popular 3+3
method is implemented as follows. At a particular dose level three patients are
randomly selected and given the drug. If there is no DLT, the dose is escalated
to the next higher one. If there are two or more DLTs, the escalation process
is stopped. If there is exactly one DLT among the three patients, three new
patients are selected at random and given the drug at the same dose. If there
are no DLTs among these three new patients, the dose is escalated. If there is
at least one DLT, the escalation process is stopped.
Assume that 30 patients are available for the trial at some fixed dose. If
among them 4 will exhibit DLT at that dose, what is the probability that in
the described step of the 3+3 procedure the dose will be escalated?
We assume that patients are selected and given the drug one by one. De-
note by A
i
the event that the ith patient will exhibit no DLT.
Then the dose will be escalated if the event
B
= A
1
A
2
A
3
∪ A
c
1
A
2
A
3
A
4
A
5
A
6
∪ A
1
A
c
2
A
3
A
4
A
5
A
6
∪ A
1
A
2
A
c
3
A
4
A
5
A
6
happens. Here, for example, the event A
1
A
c
2
A
3
A
4
A
5
A
6
means that among
the first three subjects the second experienced DLT, and that in the second
group of three there was no DLT. Since the events A
1
A
2
A
3
, A
c
1
A
2
A
3
A
4
A
5
A
6
,
A
1
A
c
2
A
3
A
4
A
5
A
6
, and A
1
A
2
A
c
3
A
4
A
5
A
6
are exclusive, the probability of their
union is the sum of probabilities:
P(B) = P(A
1
A
2
A
3
) +P(A
c
1
A
2
A
3
A
4
A
5
A
6
)
+P(A
1
A
c
2
A
3
A
4
A
5
A
6
) +P(A
1
A
2
A
c
3
A
4
A
5
A
6
).
For each of the probabilities the chain rule is needed. For example,
P(A
c
1
A
2
A
3
A
4
A
5
A
6
) =0.0739,
since

3.6 Conditional Probability and Independence 81
P(A
c
1
) ·P(A
2
|A
c
1
) ·P(A
3
|A
c
1
A
2
) ·P(A
4
|A
c
1
A
2
A
3
)
·P(A
5
|A
c
1
A
2
A
3
A
4
) ·P(A
6
|A
c
1
A
2
A
3
A
4
A
5
)
=
4
30
·
26
29
·
25
28
·
24
27
·
23
26
·
22
25
.
Thus,
P(B) =
26
30
·
25
29
·
24
28
+
4
30
·
26
29
·
25
28
·
24
27
·
23
26
·
22
25
+
26
30
·
4
29
·
25
28
·
24
27
·
23
26
·
22
25
+
26
30
·
25
29
·
4
28
·
24
27
·
23
26
·
22
25
= 0.8620.
The dose will be escalated with probability 0.8620.
If counting rules are applied, the solution can be expressed as
¡
26
3
¢¡
4
0
¢
¡
30
3
¢
+
¡
26
2
¢¡
4
1
¢
¡
30
3
¢
×
¡
24
3
¢¡
3
0
¢
¡
27
3
¢
.
The conditional odds of A given that B occurred is
Odds(A|B) =
P
(A|B)
P(A
c
|B)
=
P
(AB)
P(A
c
B)
.
If events A and B are independent, then
Odds(A|B) =Odds(A).
For two events A and B the notions of exclusiveness AB = ; and inde-
pendence
P(AB) =P(A)P(B) are often considered equivalent by some students.
Their argument can be summarized as follows. If two events do not share out-
comes and their intersection is empty, then they must be independent. The
contrary is true. If the events are exclusive and none are impossible, then
they must be dependent. This can be demonstrated with the simple example
of a coin-flipping experiment.
If A denotes tails up and B denotes heads up, then A and B are exclusive
but dependent. If we have information that A happened, then we also have
complete information that B did not happen.
If the sample spaces are different and the events are well separated in
either time or space, their independence is intuitive. However, if the events
share the sample space, it could be difficult to discern whether or not they are
independent without resorting to the definition. The following example shows
this.
Example 3.10. Let an experiment consist of drawing a card at random from a
standard deck of 52 playing cards. Define events A and B as “the card is a
♠”
82 3 Probability, Conditional Probability, and Bayes’ Rule
and “the card is a queen.” Are the events A and B independent? By definition,
P(A
·B) = P(Q♠) =
1
52
. This is the product of P(♠) =
13
52
and P(Q) =
4
52
, and
events A and B in question are independent. In this situation, intuition pro-
vides no help. Now, pretend that the 2
♥ is drawn and excluded from the deck
prior to the experiment. Events A and B become dependent since
P(A) ·P(B) =
13
51
·
4
51
6=
1
51
=P(A ·B).
The multiplication rule tells us how to find the probability for a composite
event (A
·B). The probability of (A ·B) is used in the general addition rule for
finding the probability of (A
∪B).
Rule Notation
Definitions
The conditional probability of A given B is the
probability of event A if event B occurred.
P(A|B)
A is independent of B if the conditional proba-
bility of A given B is the same as the uncondi-
tional probability of A.
P(A|B) =P(A)
Multiplication rule
The general multiplication rule for probabili-
ties.
P(A · B) = P(A)P(B|A) =
P
(B)P(A|B)
For independent events only, the multiplication
rule is simplified.
P(A ·B) =P(A)P(B)
3.6.1 Pairwise and Global Independence
If three events A, B, and C are such that any pair of them is exclusive,
i.e., AB
= ;, AC = ;, or BC = ;, then the events are mutually exclusive,
ABC
= ;. However, an analogous result does not hold for independence.
Even if the events are pairwise independent for all three pairs A,B; A,C;
and B,C, i.e.,
P(AB) = P(A)P(B), P(AC) = P(A)P(C), and P(BC) = P(B)P(C),
they may not be independent in their totality. That is, it could happen that
P(ABC) 6=P(A)P(B)P(C).
Here is one example of such a triple.

3.7 Total Probability 83
Example 3.11. The four sides of a tetrahedron (regular three-sided pyramid
with four sides consisting of isosceles triangles) are denoted by 2, 3, 5, and
30, respectively. If the tetrahedron is “rolled,” the number on the bottom side
is the outcome of interest. The three events are defined as follows: A – the
number on the bottom side is even, B – the number is divisible by 3, and C
– the number is divisible by 5. The events are pairwise independent, but in
totality, they are dependent.
The algebra is simple here, but what is the intuition? The “trick” is that
events AB, AC, BC, and ABC all coincide. In other words,
P(A|BC) = 1 even
though
P(A|B) =P(A|C) =P(A).
The concept of independence/dependence is not transitive. At first glance,
it may seem incorrect. One may argue, “If A depends on B, and B depends on
C, then A should depend on C, right?” We can demonstrate that this reasoning
is not correct with a simple example.
Example 3.12. Take a standard deck of 52 playing cards and replace the Q
♣
with Q♦. The deck still has 52 cards, two Q♦ and no Q♣. From that deck
draw a card at random and consider three events: A – the card is a queen, B
– the card is red, and C – the card is a
♥. It is easy to see that A and B are
dependent since
P(AB) =3/52 does not equal P(A)·P(B) =4/52·27/52. Events B
and C are dependent as well since event C is contained in B, and
P(BC) =P(C)
does not equal
P(B) ·P(C). However, events A and C are independent since
P(AC) =P(Q♥) =
1
52
=P(A)P(C) =
13
52
·
4
52
.
3.7 Total Probability
The rule of total probability expresses the probability of an event A as the
weighted average of its conditional probabilities. The events that A is condi-
tioned upon need to be exclusive and should partition the sample space
S .
Here are the definitions.
Events H
1
, H
2
,... , H
n
form a partition of the sample space S if
(i) they are mutually exclusive (H
i
·H
j
=;, i 6= j) and
(ii) their union is the sample space
S ,
S
n
i
=1
H
i
=S .
The events H
1
,... , H
n
are usually called hypotheses. By this definition it
follows that
P(H
1
) +···+P(H
n
) =1 (=P(S )).
Let the event of interest A happen under any of the hypotheses H
i
with a
known (conditional) probability
P(A|H
i
). Assume, in addition, that the proba-
84 3 Probability, Conditional Probability, and Bayes’ Rule
bilities of hypotheses H
1
,... , H
n
are known. P(A) can then be calculated using
the rule of total probability.
Rule of Total Probability.
P(A) =P(A|H
1
)P(H
1
) +···+P(A|H
n
)P(H
n
) (3.8)
Thus, the probability of A is a weighted average of the conditional proba-
bilities
P(A|H
i
) with weights given by P(H
i
). Since H
i
s partition the sample
space, the sum of the weights is 1.
The proof is simple. From
S = H
1
∪H
2
∪···∪H
n
it follows that
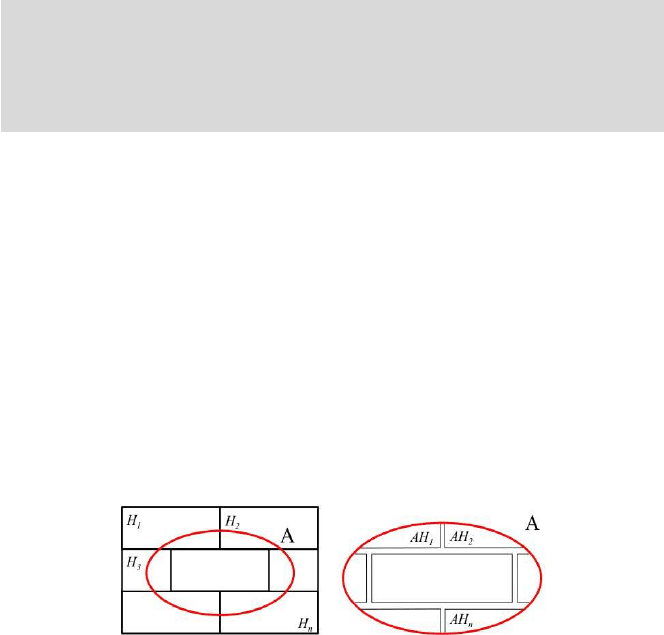
A
= AS = A(H
1
∪H
2
∪···∪H
n
) = AH
1
∪AH
2
∪···∪ AH
n
(Fig. 3.12). Events AH
i
are all exclusive and by applying the additivity prop-
erty,
P(A) =P(AH
1
) +P(AH
2
) +···+P(AH
n
).
Since each
P(AH
i
) is equal to P(A|H
i
)P(H
i
) by the multiplication rule (3.6),
the equality in (3.8) is true.
Fig. 3.12 A = A(H
1
∪H
2
∪···∪H
n
) = AH
1
∪AH
2
∪···∪AH
n
, and the events AH
i
are exclu-
sive.
Example 3.13. Two-Headed Coin. Out of 100 coins in a box, one has heads
on both sides. The rest are standard fair coins. A coin is chosen at random
from the box. Without inspecting whether it is fair or two-headed, the coin is
flipped twice. What is the probability of getting two heads?
Let A be the event that both flips resulted in heads. Let H
1
denote the
event (hypothesis) that a fair coin was chosen. Then, H
2
= H
c
1
denotes the
hypothesis that the two-headed coin was chosen.
P(A) = P(A|H
1
)P(H
1
) +P(A|H
2
)P(H
2
)
= 1/4 ·99/100 +1 ·1/100 =103/400 =0.2575.
