Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support
Подождите немного. Документ загружается.


3.8 Bayes’ Rule 85
The probability of the two flips resulting in tails is 0.2475 (check this!),
which is slightly smaller than 0.2575. Is this an influence of the two-headed
coin?
The next example is an interesting interplay between conditional and un-
conditional independence solved by the rule of total probability.
Example 3.14. Accident Proneness. Imagine a population with two types
of individuals: N normal, and N
c
accident prone. Suppose that 5/6 of these
people are normal, so that if we randomly select a person from this population
the probability that the chosen person will be normal is
P(N) = 5/6. Let A
i
be
the event that an individual has an accident in year i. For each individual A
i
is independent of A
j
whenever i 6= j.
The accident probability is different for the two classes of individuals,
P(A
i
|N) = 0.01 and P(A
i
|N
c
) = 0.1. The chance of a randomly chosen indi-
vidual having an accident in a given year is
P(A
i
) =P(A
i
|N)P(N) +P(A
i
|N
c
)P(N
c
) =0.01 ×5/6 +0.1 ×1/6 =0.025.
The probability that a randomly chosen individual has an accident in both the
first and second year follows from the rule of total probability and the fact that
A
1
and A
2
are independent for a given individual
P(A
1
∩A
2
) = P(A
1
∩A
2
|N)P(N) +P(A
1
∩A
2
|N
c
)P(N
c
)
= P(A
1
|N)P(A
2
|N)P(N) +P(A
1
|N
c
)P(A
2
|N
c
)P(N
c
)
= 0.01 ×0.01×5/6 +0.1 ×0.1 ×1/6 =0.00175.
Note that
P(A
2
|A
1
) =P(A
1
∩A
2
)P(A
2
) =0.00175/0.025 =0.07 6=0.025 =P(A
2
).
Therefore A
1
and A
2
are not (unconditionally) independent!
3.8 Bayes’ Rule
Bayes’ rule is named after Thomas Bayes, a nonconformist priest from the
eighteenth century who was among the first to use conditional probabilities.
He first introduced “inverse” probabilities, which are the special case of what
is now called Bayes’ rule (Bayes, 1763). The general form was first used by
Laplace (1774). Recall that the multiplication rule states
P(AH) =P(A)P(H|A) =P(H)P(A|H).

86 3 Probability, Conditional Probability, and Bayes’ Rule
This simple identity in association with the rule of total probability is the
essence of Bayes’ rule.
Bayes’ Rule. Let the event of interest A happen under any of the
hypotheses H
i
with a known (conditional) probability P(A|H
i
). Assume,
in addition, that the probabilities of hypotheses H
1
,... , H
n
are known
(prior probabilities). Then the conditional (posterior) probability of the
hypothesis H
i
, i =1, 2, ..., n, given that event A happened, is
P(H
i
|A) =
P
(A|H
i
)P(H
i
)
P(A)
,
where
P(A) =P(A|H
1
)P(H
1
) +···+P(A|H
n
)P(H
n
).
The proof is simple:
P(H
i
|A) =
P
(AH
i
)
P(A)
=
P
(A|H
i
)P(H
i
)
P(A)
,
where
P(A) is given by the rule of total probability.
Although Bayes’ rule is a simple formula for finding conditional probabili-
ties, it is a precursor for a coherent “statistical learning” that will be discussed
in the following chapters. It concerns the transition from prior probabilities
of hypotheses to the posterior probabilities once new information about the
sample space is obtained.
P(H)
BAYES’ RULE
−→ P(H|A)
Example 3.15. Many Flips of a Possibly Two-Headed Coin. Assume that
out of N coins in a box, one has heads on both sides, and the remaining N
−1
are fair. Assume that a coin is selected at random from the box and, without
inspecting what kind of coin it was, flipped k times. Every time the coin lands
heads up. What is the probability that the two-headed coin was selected?
Let A
k
denote the event where a randomly selected coin lands heads up k
times. The hypotheses are H
1
– the coin is two-headed, and H
2
– the coin is
fair. It is easy to see that
P(H
1
) = 1/N and P(H
2
) = (N −1)/N. The conditional
probabilities are
P(A
k
|H
1
) =1 for any k, and P(A
k
|H
2
) =1/2
k
.

3.8 Bayes’ Rule 87
By the total probability rule,
P(A
k
) =
2
k
+N −1
2
k
N
,
and by Bayes’ rule,
P(H
1
|A
k
) =
2
k
2
k
+N −1
.
For N
=1,000,000 and k = 1,2,...,40 the graph of posterior probabilities is
given in Fig. 3.13.
0 5 10 15 20 25 30 35 40
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Posterior probability of a 2H coin
Number of flips all resulting in H
Fig. 3.13 Posterior probability of a two-headed coin for N = 1,000,000 if in k flips k heads
appeared. The red dots show the posterior probabilities for k
=16 and k =24, equal to 0.0615
and 0.9437, respectively.
Note that our prior probability P(H
1
) =0.000001 jumps to a posterior prob-
ability of 0.9991 after observing 30 heads in a row. The code
twoheaded.m
calculates the probabilities and plots the graph in Fig. 3.13. It is curious to
observe how nonlinear the change of posterior probability is. This probability
is quite stable for k up to 15 and after 25. The most rapid change is in the
range 16
≤ k ≤ 24, where it increases from 0.0615 to 0.9437. This illustrates
the “learning” ability of Bayes’ rule.
Example 3.16. Prosecutor’s Fallacy. The prosecutor’s fallacy is a fallacy
commonly occurring in criminal trials but also in other various arguments
involving rare events. It consists of a subtle exchange of
P(A|B) for P(B|A). We
will explain it in the context of Example 3.15. Assume that out of N
=1,000,000
coins in a box, one is two-headed and “guilty.” Assume that a coin is selected at

88 3 Probability, Conditional Probability, and Bayes’ Rule
random from the box and, without inspection, flipped k =15 times. All k =15
times the coin lands heads up. Based on this evidence, the “prosecutor” claims
the selected coin is guilty since if it were “innocent,” the observed k
=15 heads
in a row would be extremely unlikely, with a probability of
¡
1
2
¢
15
≈ 0.00003.
But in reality, the probability that the “guilty” coin was selected and flipped
is
1
1+999999/2
15
≈ 0.03 and the prosecutor is accusing an “innocent” coin with a
probability of approx. 0.97.
Bayes’ rule is even more revealing if expressed in terms of odds.
The posterior odds of the hypothesis
H
i
are equal to the product of its
prior odds and Bayes’ factor (likelihood ratio),
Odds(H
i
|A) = BF × Odds(H
i
),
where BF
=P(A|H
i
)/P(A|H
c
i
).
Thus, the “updater” is Bayes’ factor BF, which represents the ratio of prob-
abilities of the evidence (event A) under H
i
and H
c
i
. All available information
from the experiment is contained in Bayes’ factor, and Bayesian “learning” in-
corporates this information in a coherent way by transforming the prior odds
to the posterior odds.
It is interesting to look at the log-odds equation
log
Odds(H
i
|A) =log BF+log Odds(H
i
).
If the prior log-odds log
Odds(H
i
) increase/decrease for a constant C, then the
posterior log-odds increase/decrease for the same constant, no matter what the
Bayes’ factor is. Likewise, if the log-Bayes factor increases/decreases for a con-
stant C, then the log posterior odds increase/decrease for the same constant,
no matter what the log prior odds are. This additivity property was used for
constructing nomograms for fast approximate calculation of odds mainly in a
medical context.
The log BF was also termed weight of evidence by Alan Turing, who used
similar techniques during the Second World War when breaking German
“Enigma Machine” codes.
Example 3.17. A Bridge Connection. Figure 3.14 shows a circuit S that
consists of components e
i
, i = 1,...,7 which work (and fail) independently of
each other. Note that the connection of component e
7
is neither parallel nor
serial. The components are operational in some time interval T with probabil-
ities given in the following table.
Component e
1
e
2
e
3
e
4
e
5
e
6
e
7
Probability of component working 0.3 0.8 0.2 0.2 0.5 0.6 0.4

3.8 Bayes’ Rule 89
Fig. 3.14 “Bridge” connection of e
7
.
We will calculate the posterior odds of e
7
working, given the information
that circuit S is operational.
Assume two hypotheses, H
1
– the component e
7
is operational, and H
2
=
H
c
1
– e
7
is not operational. Under hypothesis H
1
, circuit S can be expressed as
S
|H
1
= e
1
∩(e
2
∪e
4
) ∩(e
3
∪e
5
) ∩e
6
,
while under H
c
1
the expression is
S
|H
c
1
= e
1
∩((e
2
∩e
3
) ∪(e
4
∩e
5
)) ∩e
6
.
By calculations similar to that in Example 3.5 we find that
P(S|H
1
) =0.09072
and
P(S|H
c
1
) =0.04392.
Note that
P(H
1
) =P(e
7
works) =0.4 and P(H
2
) =P(H
c
1
) =0.6, so by the total
probability rule,
P(S) =0.06264. The prior odds of H
1
are Odds(H
1
) =0.4/0.6 =
2/3, and Bayes’ factor is BF = P(S|H
1
)/ P(S|H
c
1
) = 2.06557. The posterior odds
of H
1
are Odds(H
1
|S) =BF ×O dds(H
1
) =2.06557 ×2/3 =1.37705.
Thus, the odds of e
7
working increased from 0.66667 to 1.30705, after
learning that the circuit is operational. See also
bridge.m.
Example 3.18. Subsequent Transfers. In each of n boxes there are a white
and b black balls. A ball is selected at random from the first box and placed
into the second box. Then, from the second box another ball is selected at
random and transferred to the third box, and so on. Finally, from the (n
−1)th
box a ball is selected at random and transferred to the nth box.
1
%
?
&
2
%
?
&
3
%···&
n
%
◦
(a) After this series of consecutive transfers, a ball is selected from the nth
box. What is the probability that this ball will be white?
(b) If the ball drawn from the fourth box was white, what is the probability
that the first ball transferred had been white as well?

90 3 Probability, Conditional Probability, and Bayes’ Rule
Let A
i
denote the event that in the ith transfer the white ball was selected.
Then
P(A
n
) = P(A
n
|A
n−1
)P(A
n−1
) +P(A
n
|A
c
n
−1
)P(A
c
n
−1
)
=
a +1
a +b +1
P(A
n−1
) +
a
a +b +1
P(A
c
n
−1
)
=
a +P(A
n−1
)
a +b +1
.
Since
P(A
1
) =
a
a+b
, we find that
P(A
2
) =P(A
3
) =···=P(A
n
) =
a
a +b
.
(b) By Bayes’ rule,
P(A
1
|A
4
) =
P(A
4
|A
1
)P(A
1
)
P(A
4
)
=P(A
4
|A
1
).
Since
P(A
4
|A
1
) = P(A
2
A
3
A
4
|A
1
) +P(A
c
2
A
3
A
4
|A
1
) +P(A
2
A
c
3
A
4
|A
1
) +P(A
c
2
A
c
3
A
4
|A
1
)
=
a +1
a +b +1
×
a +1
a +b +1
×
a +1
a +b +1
+
b
a +b +1
×
a
a +b +1
×
a +1
a +b +1
+
a +1
a +b +1
×
b
a +b +1
×
a
a +b +1
+
b
a +b +1
×
b
a +b +1
×
a
a +b +1
=
(a +1)
3
+2ab(a +1) +ab
2
(a +b +1)
3
.
3.9 Bayesian Networks*
We will discuss simple Bayesian networks in which the nodes are events.
Many events linked in a causal network form a Bayesian net. Graphically,
Bayesian networks are directed acyclic graphs (DAGs) where the nodes repre-
sent events and directed edges capture their hierarchy and dependence. Con-
sider a simple graph in Fig. 3.15.
A B
Fig. 3.15 A −→B graph. A causes B or B is a consequence of A.
We would say that node A is a parent of B, B is a child of A, that A influ-
ences, or causes B, and B depends on A. This is captured by a directed edge
3.9 Bayesian Networks* 91
(arrow) that leads from A to B. The term acyclic in DAG relates to the fact
that a closed loop of dependencies is not allowed. In other words, there does
not exist a path consisting of nodes A
1
,... , A
n
such that
A
−→ A
1
−→···−→ A
n
−→ A .
The independence of two nodes in a DAG depends on their relative position
in the graph as well as on the knowledge of other nodes (conditioning) in the
graph. The following simple example illustrates the influence of conditioning
on independence.
Example 3.19. Let A and B be outcomes of flips of two fair coins and C be an
event that the two outcomes coincide. Thus,
P(A = H) = P(A = T) = 0.5 and
P(B = H) =P(B = T) =0.5.
A
−→ C ←− B
We are interested in P(C|A, B). Nodes A and B are marginally independent
(when we do not have evidence about C) but become dependent if the outcome
of C is known:
1
2
=P(A =T, B =T|C) 6=P(A =T|C)P(B = T|C) =
1
2
·
1
2
.
Hard evidence for a node A is evidence that the outcome of A is known.
Hard evidence about nodes is the information that we bring to the network,
and it affects the probabilities of other nodes.
Bayesian networks possess a so-called Markov property. The conditional
distribution of any node depends on its parental nodes. For instance, in the
network
A
−→ B −→ C −→ D
P(C|A, B) =P(C|B) since B is a parental node of C.
Example 3.20. Alarm. Your house has a security alarm system. The house is
located in a seismically active area and the alarm system can be occasionally
set off by an earthquake. You have two neighbors, Mary and John, who do
not know each other. If they hear the alarm, they call you, but this is not
guaranteed. They also call you from time to time just to chat.
Denote by E, B, A, J, and M the events earthquake, burglary, alarm, John’s
call, and Mary’s call took place, and by E
c
,B
c
, A
c
, J
c
, and M
c
the opposite
events. The DAG of the network is shown in Fig. 3.16.
The known (or elicited) conditional probabilities are as follows:
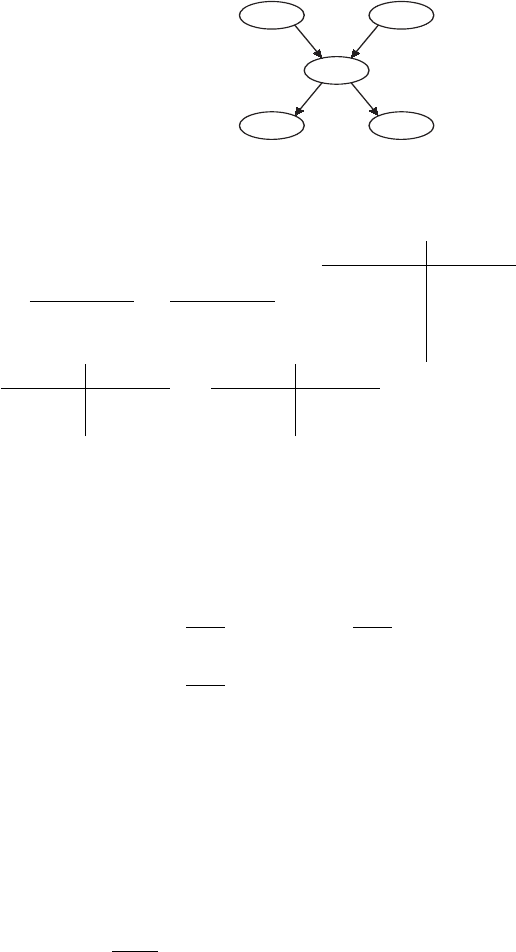
92 3 Probability, Conditional Probability, and Bayes’ Rule
B E
A
J M
Fig. 3.16 Alarm Bayesian network.
B
c
B
0.999 0.001
E
c
E
0.998 0.002
A
c
A Condition
0.999 0.001 B
c
E
c
0.71 0.29 B
c
E
0.06 0.94
B E
c
0.05 0.95 B E
J
c
J condition
0.95 0.05 A
c
0.10 0.90 A
M
c
M condition
0.99 0.01 A
c
0.30 0.70 A
We are interested in
P(J, M|B), i.e., the probability that both John and
Mary call, given the burglary.
We will first calculate this probability exactly and then find an approx-
imation using WinBUGS. If E
∗
is either E or E
c
and A
∗
either A or A
c
, we
have
P(J, M|B) =
1
P(B)
×P(B, J, M) =
1
P(B)
X
E
∗
,A
∗
P(B,E
∗
, A
∗
, J, M)
=
1
P(B)
{P(B,E)P(A|B, E)P(J, M|A)
+P(B,E
c
)P(A|B,E
c
)P(J, M|A)
+P(B,E
c
)P(A
c
|B,E
c
)P(J, M|A
c
)
+P(B,E)P(A
c
|B,E)P(J, M|A
c
)}.
Given A
∗
(either A
c
or A), P(J, M|A
∗
) = P(J|A
∗
) ×P(M|A
∗
), since John and
Mary do not know each other, and their calls can be considered independent.
After substituting the probabilities with their numerical values from the ta-
bles above, we obtain
P(J, M|B) =
1
0.001
(0.001
·0.002 ·0.95 ·0.90 ·0.70 +0.001 ·0.998 ·0.94 ·0.90 ·0.70
+ 0.001 ·0.998·0.06 ·0.05 ·0.01 +0.001 ·0.002 ·0.05 ·0.05 ·0.01)
= 0.5922.

3.9 Bayesian Networks* 93
Thus, in the case of burglary, both John and Mary will call with probability of
0.5922.
First, we approximate
P(M|B) by fixing hard evidence for a burglary. Win-
BUGS will use the code
burglary =1 and burglary = 2 in the Data part to set
the evidence that the burglary did not take place or that it took place, respec-
tively. This is the only “hard evidence” here; all other nodes remain stochastic.
The use of values 1,2 instead of the expected 0,1 is dictated by the categorical
distribution
dcat that takes only positive integers as realizations.
The WinBUGS code (
alarm.odc) is as follows:
model alarm
{
burglary ~ dcat(p.burglary[]);
earthquake ~ dcat(p.earthquake[]);
alarm ~ dcat(p.alarm[burglary, earthquake, ])
john ~ dcat(p.john[alarm,]);
mary ~ dcat(p.mary[alarm,]);
}
DATA
list(
p.earthquake=c(0.998, 0.002),
p.alarm = structure(.Data = c(0.999, 0.001,
0.71,0.29,
0.06,0.94,
0.05,0.95),
.Dim = c(2,2,2)),
p.john = structure(.Data = c(0.95,0.05,0.10,0.90),
.Dim = c(2,2)),
p.mary = structure(.Data = c(0.99,0.01,0.30,0.70),
.Dim = c(2,2)),
burglary = 2
)
INITS
list( earthquake = 1, alarm = 1, john = 1, mary = 1)
After 10,000 iterations, we obtain the mean value of M as EM =2 · p
M
+1 ·
(1 − p
M
) =1.661, that is, P(M|B) = p
M
=1.661 −1 =0.661. Any of the 1s in the
initial values
earthquake = 1, alarm = 1, john = 1, mary = 1 can be replaced
by 2, as this would not influence the final approximation.
Next, to estimate
P(J|M, B), we change WinBUGS’ data by setting B = M =
2. This is hard evidence that a burglary occurred and Mary called.
DATA
list(
p.earthquake=c(0.998, 0.002),
This probability can be approximated in WinBUGS by simulation. Note
that
P
(
J
,
M
|
B
)
=
P
(
J
|
M
,
B
)
P
(
M
|
B
) by the chain rule. The probabilities
P
(
J
|
M
,
B
)
and
P(M|B) will be approximated separately.

94 3 Probability, Conditional Probability, and Bayes’ Rule
p.alarm = structure(.Data = c(0.999, 0.001,
0.71,0.29,
0.06,0.94,
0.05,0.95), .Dim = c(2,2,2)),
p.mary = structure(.Data = c(0.99,0.01,0.30,0.70), .Dim = c(2,2)),
burglary = 2,
mary=2
)
and change the initial values to
list(earthquake = 1, alarm = 1, john = 1)
After 10,000 iterations, the mean value of J is obtained as EJ = 2 · p
J
+
(1
p
J) =1.899. Then, P(J|M,B) = p
J
=0.899. Thus, the final result is
P(J, M|B) =P(J|M,B)P(M|B) = p
J
· p
M
=0.899 ·0.661 =0.5942
(which approximates 0.5922, from the exact probability calculation).
Bayesian networks can be useful in medical diagnostics if the conditional
probabilities of the nodes are known. Here is the celebrated “Asia” example.
Example 3.21. Asia. Lauritzen and Spiegelhalter (1988) discuss a fictitious
expert system for diagnosing a patient admitted to a chest clinic, who just re-
turned from a trip to Asia and is experiencing dyspnoea.
2
A graphical model
for the underlying process is shown in Fig. 3.17, where each variable is binary.
The WinBUGS code is shown below with the conditional probabilities given as
in Lauritzen and Spiegelhalter (1988).
model Asia;
asia ~ dcat(p.asia);
smoking ~ dcat(p.smoking[]);
tuberculosis ~ dcat(p.tuberculosis[asia,]);
lung.cancer ~ dcat(p.lung.cancer[smoking,]);
bronchitis ~ dcat(p.bronchitis[smoking,]);
either <- max(tuberculosis,lung.cancer);
xray ~ dcat(p.xray[either,]);
dyspnoea ~ dcat(p.dyspnoea[either,bronchitis,])
DATA
list(asia = 2, dyspnoea = 2,
p.tuberculosis = structure(.Data = c(0.99,0.01,0.95,0.05),
.Dim = c(2,2)),
p.bronchitis = structure(.Data = c(0.70,0.30,0.40,0.60),
.Dim = c(2,2)),
p.smoking = c(0.50,0.50),
2
Difficulty in breathing, often associated with lung or heart disease and resulting in short-
ness of breath. Also called air hunger.
